leetcode算法（94.二叉树的中序遍历）

二叉树递归遍历（中序遍历）

复制代码

      1
     / \
    2   3
   / \
  4   5

中序遍历顺序：左子树 → 根节点 → 右子树

执行过程：
1. inorderTraversal(节点1)
   │ 创建空vector: result = []
   │ 
   └─ traversal(节点1, result)
      │
      ├─ traversal(节点2, result)
      │  │
      │  ├─ traversal(节点4, result)
      │  │  │
      │  │  ├─ traversal(左空) → 返回
      │  │  │
      │  │  ├─ result.push_back(4) → result = [4]
      │  │  │
      │  │  └─ traversal(右空) → 返回
      │  │
      │  ├─ result.push_back(2) → result = [4,2]
      │  │
      │  └─ traversal(节点5, result)
      │     │
      │     ├─ traversal(左空) → 返回
      │     │
      │     ├─ result.push_back(5) → result = [4,2,5]
      │     │
      │     └─ traversal(右空) → 返回
      │
      ├─ result.push_back(1) → result = [4,2,5,1]
      │
      └─ traversal(节点3, result)
         │
         ├─ traversal(左空) → 返回
         │
         ├─ result.push_back(3) → result = [4,2,5,1,3]
         │
         └─ traversal(右空) → 返回

最终结果：result = [4,2,5,1,3]

cpp 复制代码

class Solution {
public:
    // 中序遍历递归辅助函数
    // 参数：
    //   cur - 当前遍历到的树节点指针
    //   vec - 存储遍历结果的vector的引用
    void traversal(TreeNode *cur, vector<int> &vec) {
        // 递归终止条件：当前节点为空
        // 表示已经到达叶子节点的子节点，需要返回
        if (cur == NULL) return;
        
        // 递归遍历左子树
        // 遵循"左-中-右"的顺序，先处理所有左子节点
        traversal(cur->left, vec);
        
        // 访问当前节点（"中"的部分）
        // 在左子树遍历完成后，将当前节点的值添加到结果中
        vec.push_back(cur->val);
        
        // 递归遍历右子树
        // 左子树和当前节点都处理完后，再处理右子树
        traversal(cur->right, vec);
    }
    
    // 中序遍历的主函数
    // 参数：
    //   root - 二叉树的根节点指针
    // 返回值：
    //   vector<int> - 按中序遍历顺序存储的节点值数组
    vector<int> inorderTraversal(TreeNode* root) {
        // 创建一个空的vector容器，用于存储遍历结果
        vector<int> result;
        
        // 调用递归函数开始遍历
        // 从根节点开始，result以引用方式传递
        traversal(root, result);
        
        // 返回完整的遍历结果
        return result;
        
    }
};

中序遍历（迭代法）

为什么前序遍历的代码，不能和中序遍历通用呢，因为前序遍历的顺序是中左右，先访问的元素是中间节点，要处理的元素也是中间节点，所以才能写出相对简洁的代码，因为要访问的元素和要处理的元素顺序是一致的，都是中间节点。

那么再看看中序遍历，中序遍历是左中右，先访问的是二叉树顶部的节点，然后一层一层向下访问，直到到达树左面的最底部，再开始处理节点（也就是在把节点的数值放进result数组中），这就造成了处理顺序和访问顺序是不一致的。

那么在使用迭代法写中序遍历，就需要借用指针的遍历来帮助访问节点，栈则用来处理节点上的元素。

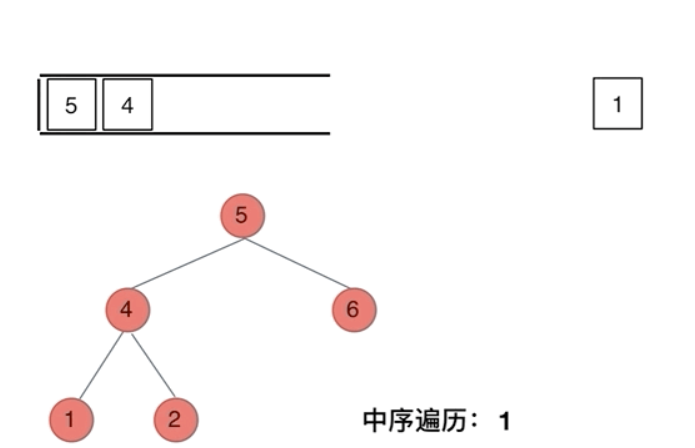
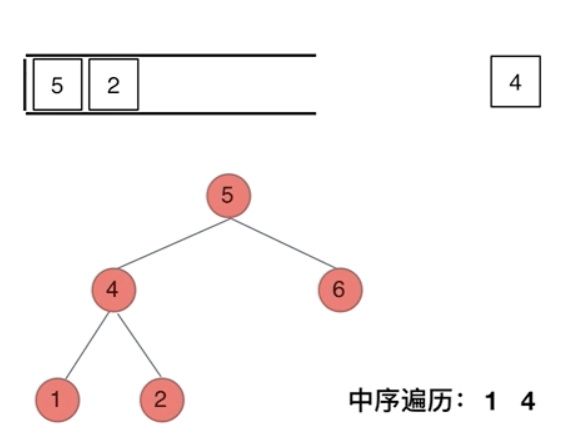
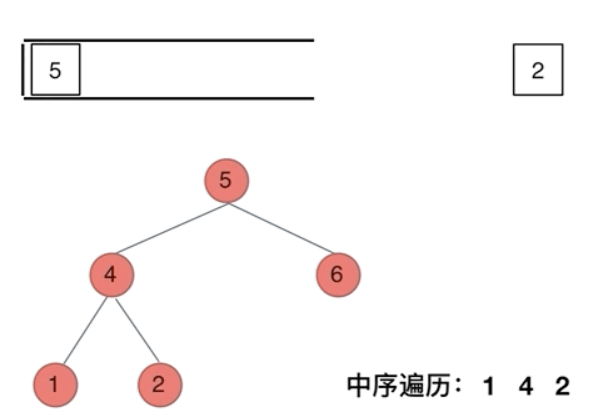
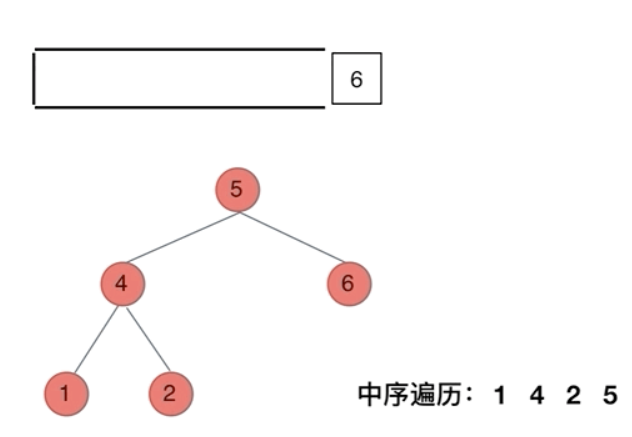
cur 指针 ：负责向下探索左子树，直到最左侧
stack ：存储已经经过但还未处理的节点（等待处理自身和右子树）

cpp 复制代码

// ❌
stack<TreeNode*> st;
st.push(root);  // 直接将根节点入栈
while (!st.empty()) {
    TreeNode* node = st.top();
    st.pop();
}
//如果刚开始只将根节点入栈，之后立马又将根节点出栈。

cpp 复制代码

TreeNode* cur = root;
while (!st.empty()) {  // 初始时栈是空的！
    // 如果root是NULL，直接跳过循环 ✅
    // 但如果root不为NULL，但刚开始的栈为空，根本不会进入循环！ ❌
}

情况1：空树

cpp 复制代码

TreeNode* cur = NULL;  // root为NULL
while (cur != NULL || !st.empty()) {
    // 条件：false || false = false，不进入 ✅
}

情况2：只有根节点

cpp 复制代码

// 初始：cur=root(不为空)，st=[]
// 循环：true || false = true，进入
// 然后压栈，cur向左为NULL
// 回溯处理根节点 ✅

 while (cur != NULL || !st.empty()) {
      if (cur != NULL) { // 指针来访问节点，访问到最底层
          st.push(cur); // 将访问的节点放进栈
          cur = cur->left;                // 左
      } else {
          cur = st.top(); // 从栈里弹出的数据，就是要处理的数据（放进result数组里的数据）
          st.pop();
          result.push_back(cur->val);     // 中
          cur = cur->right;               // 右
      }
}

cpp 复制代码

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        // 存储中序遍历结果的数组
        vector<int> result;
        // 辅助栈，用于模拟递归过程
        stack<TreeNode*> st;
        // 当前访问的节点指针
        TreeNode* cur = root;
        
        // 循环条件：当前节点不为空 或 栈不为空
        // 两个条件满足其一说明还有节点需要处理
        while (cur != NULL || !st.empty()) {
            if (cur != NULL) { // 当前节点不为空
                // 将当前节点压入栈中（相当于递归调用的入栈）
                st.push(cur);
                // 继续访问左子节点（深度优先遍历左子树）
                cur = cur->left;                // 左
            } else { // 当前节点为空，说明左子树已经遍历完毕
                // 弹出栈顶节点，这个节点就是当前要处理的节点
                cur = st.top();
                st.pop();
                // 将当前节点的值加入结果数组（访问"根"节点）
                result.push_back(cur->val);     // 中
                // 转向处理右子树
                cur = cur->right;               // 右
            }
        }
        // 返回中序遍历结果
        return result;
    }
};