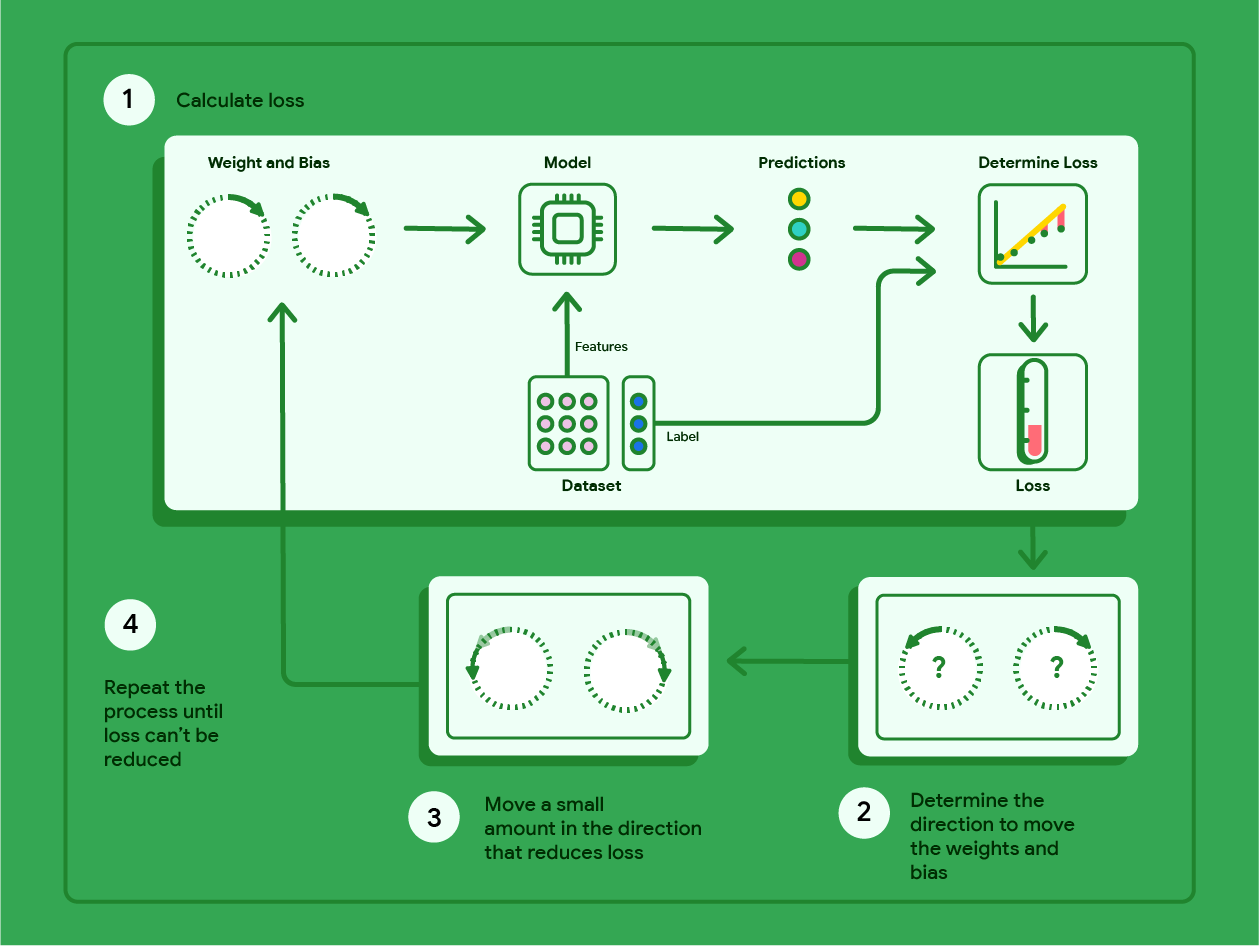
这张图其实把**梯度下降(Gradient Descent)**的训练过程画成了一个"循环流水线",核心就是:用当前参数做预测 → 算误差(loss)→ 计算往哪边改参数会让误差变小 → 小步更新参数 → 重复。
下面我按图里的 1→2→3→4,把每一步讲清楚,并配上线性回归最常见的公式。
图里每个模块在说什么
-
Dataset(数据集):分成两部分
-
Features:输入特征 x
-
Label:真实答案 y
-
-
Weight and Bias(权重和偏置):就是要训练的参数
-
权重 w(可能是向量)
-
偏置 b
-
-
Model(模型):用 w,b 把 x 变成预测值
-
Predictions(预测):y^
-
Determine Loss(计算损失):把 y^ 和 y 做对比得到 loss(温度计越高说明错得越多)
1) Calculate loss:前向计算 + 算损失
以线性回归为例:
① 用当前参数做预测(前向)
(多特征时:)
② 用预测和真实值算损失(比如 MSE)
这一步对应图中:Dataset → Model → Predictions → Determine Loss → Loss。
2) Determine direction:算"往哪边改参数才会让 loss 下降"(梯度)
这里的"方向"就是梯度:对参数求偏导。
对单变量线性回归():
直观理解:
-
是"预测偏高/偏低"的方向与幅度
-
乘上
会告诉你"斜率 w"该怎么调
-
对 b 来说就是整体偏移量该怎么调
图里右下角两个带问号的圈,就是在问:w 和 b 应该往哪边拧?
3) Move a small amount:按这个方向"小步走"(参数更新)
梯度指向的是 loss 增长最快的方向,所以要想下降,要走反方向:
-
η 叫学习率(learning rate):步子大小
-
太大:可能来回震荡甚至发散
-
太小:下降很慢
-
这一步就是图中第 3 步:"Move a small amount in the direction that reduces loss"。
4) Repeat:重复直到 loss 不能再明显降低(停止条件)
你不断循环 1→2→3,直到满足某个停止条件,例如:
-
loss 的下降小于阈值:∣Lt−Lt−1∣<ϵ
-
梯度很小:
-
达到最大迭代次数(epochs / steps)
这就是图里第 4 步:"Repeat the process until loss can't be reduced"。
把整套流程写成"训练循环"(你一眼就能对照图)
-
初始化 w,b(随机或 0)
-
循环:
-
用 w,b 算 y^
-
算 loss:L(w,b)
-
算梯度:
-
更新:
-
-
直到满足停止条件
我用一个超小数据集 ,把图里的 1→2→3→4 跑两三轮给你看,保证每一步都能对上号。
例子数据(线性回归)
我们希望学到 y≈wx+b。
数据集(3 个点):
| i | Xi | Yi |
|---|---|---|
| 1 | 1 | 2 |
| 2 | 2 | 4 |
| 3 | 3 | 6 |
损失函数用 MSE:
梯度(你在第 2 步会用到):
学习率取 η=0.1。
第 0 轮(初始化)
设
1) 预测 + 算 loss
误差
2) 算梯度(方向)
3) 小步更新参数(走"负梯度")
第 1 轮(用 w1,b1 再来一次)
1) 预测 + 算 loss
-
, 误差
-
, 误差
-
, 误差
loss:
(你看:从 18.67 直接掉到 0.296,说明"方向 + 小步更新"有效。)
2) 算梯度
3) 更新
第 2 轮(再看一次 loss)
用 :
-
, 误差
-
, 误差
-
, 误差
loss 继续下降 ✅
这和图里 1→2→3→4 的对应关系
-
1 Calculate loss:算 y^ 和 L
-
2 Determine direction :算梯度
-
3 Move a small amount:w,b 用学习率 η 小步更新
-
4 Repeat:loss 不怎么降了就停
我也可以把 loss 看成"温度",梯度看成"哪个旋钮(w/b)往哪拧会降温",再用同一组数据画出 loss 曲线(迭代次数 vs loss),你会更直观看到下降过程。
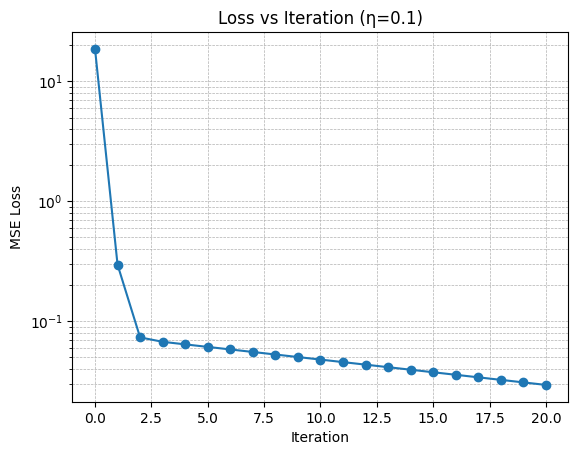
我把刚才那组"玩具数据"继续往下迭代了 20 次(学习率 η=0.1),并把每一轮的:
-
参数:w,b
-
当前损失:MSE loss
-
梯度:
都列成了一张表(你现在应该能在界面里看到 Gradient Descent Iterations 的表格),同时画了一张 Loss vs Iteration 曲线图。
你可以从图上直观看到这件事:
1) loss 一开始下降非常快
-
第 0 轮 loss 很大(18.67)
-
第 1 轮直接降到 0.296
-
第 2 轮再降到 0.0734
这对应你图里第 1 步的"温度计",温度快速降下来了。
2) 后面下降变慢(接近最优点)
当 w,bw,bw,b 已经很接近最优解时,梯度会变小(表格里你会看到 dL/dw、dL/db 逐步变小),于是每次更新带来的改进也变小------这就是曲线后半段"变平"的原因。
3) 为什么要用对数坐标(log)
我在 loss 曲线用的是 log 纵轴,这样你能同时看清:
-
前期的"断崖式下降"
-
后期的"缓慢逼近"
也可以把它和图片里的 4 个步骤更强绑定,按指定的某一轮(比如第 1 轮),把那一轮的:
-
y^(预测点)
-
误差 e
-
loss
-
梯度
-
更新后的 w,b
一项项拆开写出来,让你像"走迷宫"一样对照图里的箭头走一圈。
我们就把第 1 轮 、第 2 轮 按图里的 1→2→3 (算预测/损失 → 算方向(梯度) → 小步更新)完整走一遍。
(这里"第 1 轮"指:用 (w1,b1) 去算 loss/梯度并更新到 (w2,b2);"第 2 轮"指:用 (w2,b2) 更新到 (w3,b3)。)
数据:,学习率 η=0.1,损失 MSE
梯度:
先给出上一轮结果(第 0 轮更新后)
初始化 更新后得到:
第 1 轮(用  → 更新到
→ 更新到  )
)
1) 预测 y^ + loss
对 3 个点逐个算:
点 1:x=1,y=2
点 2:x=2,y=4
点 3:x=3,y=6
loss:
这一步就是图里的:Dataset → Model → Predictions → Determine Loss → Loss。
2) 计算方向(梯度)
先算两个求和项:
这一步就是图里的第 2 步:"Determine the direction to move the weights and bias"。
3) 小步更新参数(梯度下降)
这一步就是图里的第 3 步:"Move a small amount ..."。
第 2 轮(用 w2,b2 → 更新到 w3,b3)
现在从:
开始。
1) 预测 + loss
点 1:x=1,y=2
点 2:x=2,y=4
点 3:x=3,y=6
loss:
(注意:第 3 个点误差变成负的,意思是它开始"预测偏低"了。)
2) 梯度

3) 更新到 w3,b3
你现在能读懂"方向"了吗?
看第 2 轮的梯度很关键:
-
是负数
更新 w←w−η(负数)就会让 w 增大
(我们确实看到 w 从 1.6711 → 1.7007)
-
是正数
更新后 b 变小
(0.6933 → 0.6862)
这就是图里第 2 步"决定往哪边拧旋钮",第 3 步"拧一点点"。