分类与回归算法（二） - 线性回归

大数据魔法师2025-11-05 19:56

文章目录

  • 一、什么是线性回归
  • 二、线性回归的核心原理
    • [1. 损失函数](#1. 损失函数)
    • [2. 优化算法](#2. 优化算法)
      • [2.1 正规方程](#2.1 正规方程)
      • [2.2 梯度下降](#2.2 梯度下降)
  • 三、线性回归的应用场景
  • 四、线性回归实现步骤
    • [1. 数据收集与加载](#1. 数据收集与加载)
      • [1.1 数据集介绍](#1.1 数据集介绍)
        • [1.1.1 数据集基本信息](#1.1.1 数据集基本信息)
        • [1.1.2 数据集背景与用途](#1.1.2 数据集背景与用途)
        • [1.1.3 特征说明（13 个自变量）](#1.1.3 特征说明（13 个自变量）)
      • [1.2 数据加载](#1.2 数据加载)
        • [1.2.1 数据加载相关方法](#1.2.1 数据加载相关方法)
          • [（1） fetch_openml(name, version, as_frame)](#（1） fetch_openml(name, version, as_frame))
          • （2）.values
          • [（3）pd.DataFrame(data, columns)](#（3）pd.DataFrame(data, columns))
          • [（4）pd.Series(data, name)](#（4）pd.Series(data, name))
        • [1.2.2 数据加载代码](#1.2.2 数据加载代码)
    • [2. 数据探索与可视化（EDA）](#2. 数据探索与可视化（EDA）)
      • [2.1 EDA相关方法介绍](#2.1 EDA相关方法介绍)
      • [2.2 EDA实现步骤及代码](#2.2 EDA实现步骤及代码)
        • [2.2.1 查看前5行数据](#2.2.1 查看前5行数据)
        • [2.2.2 查看数据摘要信息](#2.2.2 查看数据摘要信息)
        • [2.2.3 描述性统计分析](#2.2.3 描述性统计分析)
        • [2.2.4 目标变量分布分析](#2.2.4 目标变量分布分析)
        • [2.2.5 目标变量与各个特征变量的相关性分析](#2.2.5 目标变量与各个特征变量的相关性分析)
        • [2.2.6 验证变量间的真实关系](#2.2.6 验证变量间的真实关系)
        • [2.2.7 特征间的相关性分析](#2.2.7 特征间的相关性分析)
      • [2.3 EDA 完整代码](#2.3 EDA 完整代码)
    • [3. 数据预处理](#3. 数据预处理)
      • [3.1 处理缺失值](#3.1 处理缺失值)
      • [3.2 特征选择](#3.2 特征选择)
        • [3.2.1 特征选择相关方法](#3.2.1 特征选择相关方法)
        • [3.2.2 特征选择：基于相关性与多重共线性分析的优化筛选](#3.2.2 特征选择：基于相关性与多重共线性分析的优化筛选)
      • [3.3 数据标准化（归一化）](#3.3 数据标准化（归一化）)
        • [3.3.1 数据标准化相关方法](#3.3.1 数据标准化相关方法)
        • [3.3.2 数据标准化](#3.3.2 数据标准化)
      • [3.4 划分训练集与测试集](#3.4 划分训练集与测试集)
        • [3.4.1 相关方法说明](#3.4.1 相关方法说明)
        • [3.4.2 划分训练集与测试集代码实现](#3.4.2 划分训练集与测试集代码实现)
      • [3.5 预处理总结](#3.5 预处理总结)
    • [4. 构建线性回归模型](#4. 构建线性回归模型)
      • [4.1 相关方法说明](#4.1 相关方法说明)
        • [4.1.1 `LinearRegression`构造方法简介](#4.1.1 LinearRegression构造方法简介)
        • [4.1.2 `LinearRegression`构造方法参数说明](#4.1.2 LinearRegression构造方法参数说明)
        • [4.1.3 `LinearRegression`的核心属性（模型训练后可用）](#4.1.3 LinearRegression的核心属性（模型训练后可用）)
        • [4.1.4 `LinearRegression`对象的核心方法](#4.1.4 LinearRegression对象的核心方法)
      • [4.2 构建线性回归模型代码实现](#4.2 构建线性回归模型代码实现)
    • [5. 模型预测](#5. 模型预测)
      • [5.1 模型预测相关方法](#5.1 模型预测相关方法)
      • [5.2 模型预测代码实现](#5.2 模型预测代码实现)
    • [6. 模型评估](#6. 模型评估)
      • [6.1 常用评估指标说明](#6.1 常用评估指标说明)
      • [6.2 评估代码实现与结果分析](#6.2 评估代码实现与结果分析)
    • [7. 结果可视化](#7. 结果可视化)
      • [7.1 真实房价 vs 预测房价（散点图）](#7.1 真实房价 vs 预测房价（散点图）)
      • [7.2 预测误差分布（直方图）](#7.2 预测误差分布（直方图）)
      • [7.3 特征重要性（基于回归系数绝对值）](#7.3 特征重要性（基于回归系数绝对值）)
      • [7.4 结果解读](#7.4 结果解读)
    • [8. 模型解释](#8. 模型解释)
      • [8.1 回归系数的业务含义](#8.1 回归系数的业务含义)
      • [8.2 特征重要性与决策支持](#8.2 特征重要性与决策支持)
      • [8.3 模型的实际应用价值](#8.3 模型的实际应用价值)
      • [8.4 局限性与改进方向](#8.4 局限性与改进方向)
  • 五、完整代码
    • [1. 完整代码](#1. 完整代码)
    • [2. 优化后完整代码](#2. 优化后完整代码)

一、什么是线性回归

线性回归的本质是构建特征与目标值之间的线性关系模型 ，通过学习数据中的规律，实现对连续数值的预测。

举个生活中的例子：假设我们想预测"房屋售价"（目标值），影响售价的因素可能有"房屋面积""卧室数量""楼层"（特征）。线性回归会假设这些特征与售价呈线性关系，最终得到一个类似这样的公式：
房屋售价 = 0.8×面积 + 0.3×卧室数量 + 0.1×楼层 + 50

其中，"0.8、0.3、0.1"是特征的"权重"（表示该特征对目标值的影响程度），"50"是"截距"（基础价格）。通过这个公式，输入新房屋的特征，就能预测出它的售价。

从数学角度定义：若有(n)个特征（( x 1 , x 2 , . . . , x n x_1, x_2, ..., x_n x1,x2,...,xn)），目标值为(y)，线性回归模型可表示为：
y = w 1 x 1 + w 2 x 2 + . . . + w n x n + b y = w_1x_1 + w_2x_2 + ... + w_nx_n + b y=w1x1+w2x2+...+wnxn+b 其中：

  • ( w 1 , w 2 , . . . , w n w_1, w_2, ..., w_n w1,w2,...,wn)：特征权重（也称"回归系数"），决定每个特征对(y)的影响方向和大小；
  • ( b b b)：截距（也称"偏置项"），表示所有特征为0时，目标值的基础水平；
  • ( y y y)：模型预测的目标值（连续数值）。

二、线性回归的核心原理

线性回归的关键是求解最优的权重( w w w)和截距( b b b)，使得模型的预测值与真实值的偏差最小。这一过程需要通过"损失函数"定义偏差，再通过"优化算法"最小化损失函数。

1. 损失函数

损失函数用于衡量模型的"偏差大小" ，用"残差"表示单个样本的预测偏差：残差 = 真实值 - 预测值，即( y i − y ^ i y_i - \hat{y}_i yi−y^i)，其中( y ^ i \hat{y}_i y^i)是第( i i i)个样本的预测值。

线性回归常用均方误差（MSE） 作为损失函数，它是所有样本残差的平方和的平均值，公式为：
L o s s = M S E = 1 m ∑ i = 1 m ( y i − y ^ i ) 2 Loss = MSE = \frac{1}{m} \sum_{i=1}^m (y_i - \hat{y}_i)^2 Loss=MSE=m1i=1∑m(yi−y^i)2 其中( m m m)是样本数量。

为什么选择MSE？

  • 平方项能放大"大偏差"的影响，强制模型优先降低极端错误（如预测房价偏差100万，平方后会远大于偏差10万的样本）；
  • MSE是光滑可导的函数，便于后续用"梯度下降"等优化算法求解最小值。

2. 优化算法

优化算法用于找到最小损失对应的( w w w)和( b b b) ，求解( w w w)和( b b b)有两种经典方法："正规方程"和"梯度下降"，适用于不同的样本规模。

2.1 正规方程

正规方程可用于直接计算最优解 ，对于简单的线性回归（如单特征），可通过数学推导直接求出( w w w)和( b b b)的解。

以单特征线性回归 （仅1个特征 x x x）为例：

  • 截距 b b b 的计算公式：( b = y ˉ − w x ˉ b = \bar{y} - w\bar{x} b=yˉ−wxˉ)（其中 x ˉ \bar{x} xˉ 是特征的平均值， y ˉ \bar{y} yˉ 是目标值的平均值）；
  • 权重 w w w 的计算公式：( w = ∑ i = 1 m ( x i − x ˉ ) ( y i − y ˉ ) ∑ i = 1 m ( x i − x ˉ ) 2 w = \frac{\sum_{i=1}^m (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^m (x_i - \bar{x})^2} w=∑i=1m(xi−xˉ)2∑i=1m(xi−xˉ)(yi−yˉ))。

适用场景 ：样本量小（如 m < 10000 m < 10000 m<10000）、特征少的场景，计算速度快；但当样本量或特征数过大时，矩阵求逆运算会非常耗时（时间复杂度 O ( n 3 ) O(n^3) O(n3)， n n n 为特征数）。

2.2 梯度下降

梯度下降用于迭代逼近最优解 ，当样本量或特征数较大时，梯度下降是更高效的选择。它的核心思想是：沿着损失函数的梯度方向，逐步调整 w w w 和 b b b，直到损失函数达到最小值。

核心步骤：

  1. 初始化 w w w（如随机赋值）和 b b b（如赋值0）；
  2. 计算当前 w w w 和 b b b 对应的损失函数值；
  3. 计算损失函数对 w w w 和 b b b 的"梯度"（即偏导数，反映参数变化对损失的影响方向）；
  4. 沿梯度负方向更新 w w w 和 b b b （学习率 α \alpha α 控制每次更新的步长）：
    ( w = w − α × ∂ L o s s ∂ w w = w - \alpha \times \frac{\partial Loss}{\partial w} w=w−α×∂w∂Loss)
    ( b = b − α × ∂ L o s s ∂ b b = b - \alpha \times \frac{\partial Loss}{\partial b} b=b−α×∂b∂Loss)；
  5. 重复步骤2-4，直到损失函数收敛（变化小于阈值）或达到最大迭代次数。

关键参数：

  • 学习率 α \alpha α：步长过大会导致损失函数震荡不收敛，步长过小会导致训练速度极慢，通常需要通过交叉验证调优（如取值0.001、0.01、0.1）；
  • 迭代次数：需设置合理的最大迭代次数，避免训练时间过长。

适用场景 ：样本量大（如 m > 10000 m > 10000 m>10000）、特征多的场景，时间复杂度低 O ( m n ) O(mn) O(mn)，是工业界常用的优化方法。

三、线性回归的应用场景

行业领域 应用场景 输入特征（自变量） 输出目标（因变量） 是否适用线性回归 备注
房地产 房价预测 面积、房间数、地理位置、房龄、楼层 房屋价格（万元） ✅ 适用 经典应用，解释性强
市场营销 销售额预测 广告投入（电视/网络/报纸）、促销力度 销售额（万元） ✅ 适用 可分析各渠道贡献度
金融 信用额度评估 收入、工作年限、信用记录、负债比 授信额度（元） ✅ 适用（初步模型） 常与其他模型结合使用
医疗健康 血糖水平预测 年龄、体重、饮食热量、运动时间 血糖值（mmol/L） ✅ 适用（简化模型） 用于趋势分析，非精确诊断
教育 学生成绩预测 学习时长、出勤率、作业完成度 考试成绩（分） ✅ 适用 可帮助教师识别影响因素
气象 气温趋势预测 历史温度、季节、湿度、风速 未来气温（℃） ✅ 适用（短期） 长期预测需更复杂模型
农业 农作物产量预测 降雨量、施肥量、光照时间、土壤肥力 亩产量（公斤） ✅ 适用 辅助农业决策
交通 出行时间预测 距离、路况、时间段、天气 行驶时间（分钟） ✅ 适用 导航系统常用基础模型
能源 电力消耗预测 气温、人口、工业活动指数 日用电量（千瓦时） ✅ 适用 用于电网调度规划
保险 理赔金额预测 年龄、保额、健康状况、事故类型 理赔金额（元） ✅ 适用 控制赔付风险
电子商务 用户消费预测 浏览时长、购买频率、优惠券使用 年消费金额（元） ✅ 适用 用于个性化推荐
环境 空气质量指数（AQI）预测 PM2.5、PM10、NO₂、湿度、风速 AQI 数值 ✅ 适用（短期） 需结合时间序列方法
制造业 设备故障时间预测 使用时长、维护次数、温度、振动频率 剩余使用寿命（小时） ⚠️ 有限适用 若关系非线性需改用其他模型
股票市场 股价走势预测 历史价格、交易量、市盈率 明日收盘价（元） ❌ 不推荐 股市高度非线性、噪声大
社交媒体 用户活跃度预测 发帖数、点赞数、关注数 活跃分数（0--100） ✅ 适用（简化） 可作为用户分层依据

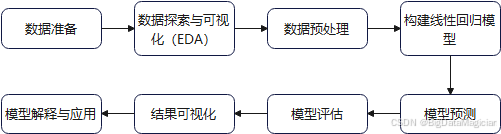
四、线性回归实现步骤

如图所示，线性回归模型的构建与应用遵循一个系统化、结构化的流程。整个过程可分为八个关键阶段，形成从数据输入到模型输出的完整闭环，涵盖数据处理、建模、评估与部署等核心环节。

1. 数据收集与加载

此处以"波士顿房价预测"数据集（经典回归任务，目标是根据房屋特征预测房价）为例，用Python的scikit-learn库实现线性回归，同时用matplotlib可视化结果。

1.1 数据集介绍

1.1.1 数据集基本信息
属性 内容
名称 Boston House Prices Dataset
来源 UCI 机器学习仓库（通过 OpenML 平台提供）
获取方式 sklearn.datasets.fetch_openml(name="boston", version=1)
任务类型 回归（Regression）
样本数量 506 条记录
特征数量 13 个数值型/类别型特征
目标变量 MEDV：房屋中位数价格（单位：千美元）
发布时间 20 世纪 70 年代初（基于 1978 年数据）
1.1.2 数据集背景与用途

该数据集最初由美国统计学家 Harrison 和 Rubinfeld 在 1978 年研究波士顿地区住房价格影响因素时收集。它广泛用于机器学习入门教学（线性回归、决策树等）、特征工程练习、模型评估基准测试。

1.1.3 特征说明（13 个自变量）

所有特征均为连续值或离散比例值，具体如下：

字段 名称 含义 与房价关系
CRIM Crime Rate 城镇人均犯罪率 负相关
ZN Residential Zoning 占地超过 25,000 平方英尺的住宅用地比例 正相关
INDUS Non-Retail Business 非零售商业用地占比（英亩/城镇） 负相关
CHAS Charles River Dummy 是否临查尔斯河（1=是，0=否） 正相关
NOX Nitric Oxides Concentration 一氧化氮浓度（ppm） 负相关
RM Average Rooms per Dwelling 每栋住宅平均房间数 强正相关
AGE Proportion of Old Units 1940 年前建造的自住单位比例 负相关
DIS Weighted Distances to Employment Centers 到五个就业中心的加权距离 正相关
RAD Accessibility to Highways 高速公路可达指数（越小越难达） 复杂关系
TAX Property Tax Rate 每万美元的全额房产税率 负相关
PTRATIO Pupil-Teacher Ratio 城镇师生比 负相关
B 1000 ( B k − 0.63 ) 2 1000(Bk - 0.63)^2 1000(Bk−0.63)2 黑人比例相关指标（有争议） ------
LSTAT Lower Status Population % 低收入人群百分比 强负相关

🔍 目标变量：

  • MEDV：自有住房的中位数价值（Median value of owner-occupied homes in $1000s），即我们要预测的目标。

1.2 数据加载

1.2.1 数据加载相关方法
（1） fetch_openml(name, version, as_frame)

这是 scikit-learn 提供的用于从 OpenML（开放机器学习平台）下载标准数据集的核心函数，替代已被弃用的 load_boston()。

参数 类型 默认值 说明
name str 必填 指定要加载的数据集名称，例如 "boston"、"iris"
version int 或 str None 指定数据集版本号，如 1；若存在多个版本需明确指定
as_frame bool False 是否将特征和目标返回为 pandas.DataFrame 和 Series： • True：便于数据分析 • False：返回 NumPy 数组（传统格式）
parser str 'auto' 解析器类型，推荐设置为 'pandas' 以确保兼容性（尤其在新版本 sklearn 中）
return_X_y bool False 若为 True，则只返回 (data, target) 元组，不返回完整 Bunch 对象

🔍 返回值 ：一个 Bunch 对象，包含：

  • .data：特征矩阵（DataFrame 或 array）
  • .target：目标向量（Series 或 array）
  • .feature_names：特征名称列表
  • .DESCR：数据集描述（部分数据集提供）
（2）.values

这是 pandas.DataFrame 和 pandas.Series 提供的属性，用于将数据转换为 NumPy 数组。

属性 来源 返回类型 说明
.values pandas.DataFrame, pandas.Series numpy.ndarray 将 DataFrame 转为二维数组，Series 转为一维数组
（3）pd.DataFrame(data, columns)

用于创建 pandas 的二维数据结构，适合处理表格型数据。

参数 类型 是否必需 说明
data array-like, dict, DataFrame 等 是 输入数据，此处为 boston.data.values（二维数组）
columns list of str 否（建议使用） 指定列名，提升可读性；使用 boston.feature_names 可保留原始命名
（4）pd.Series(data, name)

用于创建一维标签数组，常用于表示目标变量（标签或连续值）。

参数 类型 是否必需 说明
data array-like 是 目标值数组，如 boston.target.values
name str 否（强烈建议） 给 Series 命名，便于识别含义（如 "MEDV" 表示房价中位数）
1.2.2 数据加载代码
python 复制代码 
# 1. 导入库
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.datasets import fetch_openml
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split

# 设置matplotlib的中文字体为SimHei（黑体），以确保中文标签可以正常显示。
plt.rcParams['font.sans-serif'] = ['SimHei']
# 解决负号'-'显示为方块的问题，通过设置'axes.unicode_minus'为False来实现。
plt.rcParams['axes.unicode_minus'] = False

# 设置全局选项
pd.set_option('display.max_columns', None)  # 显示所有列
pd.set_option('display.width', None)  # 自动检测宽度
pd.set_option('display.max_colwidth', 50)  # 列内容最多显示50字符
pd.set_option('display.expand_frame_repr', False)  # 禁用多行表示（可选）

# 2. 加载并查看数据（波士顿房价数据集）

# 使用 sklearn 的 fetch_openml 函数从 OpenML 平台下载 "boston" 数据集
# - name="boston": 指定数据集名称
# - version=1: 使用第一个版本
# - as_frame=True: 返回结果包含 pandas DataFrame 和 Series（便于后续分析）
boston = fetch_openml(name="boston", version=1, as_frame=True, parser="pandas")

# 将特征数据（boston.data）转换为 NumPy 数组
# 原因：虽然 as_frame=True 返回的是 DataFrame，但某些旧版代码或模型要求输入为数组格式
# .values 属性将 DataFrame 转换为二维 numpy 数组
boston.data = boston.data.values

# 将目标变量（boston.target）也转换为 NumPy 数组
# 如果 target 是 DataFrame 或 Series，.values 可确保其变为一维数组
boston.target = boston.target.values

# 将特征数据重新构造成 pandas DataFrame，方便查看和操作
# - boston.data: 已转为 numpy 数组的特征矩阵
# - columns=boston.feature_names: 使用原始数据集中定义的特征名称作为列名
X = pd.DataFrame(boston.data, columns=boston.feature_names)

# 构造目标变量 y，使用 pd.Series 存储
# - boston.target: 目标值数组（房屋中位价格，单位：千美元）
# - name="MEDV": 给 Series 命名为 MEDV（Median Value），与原始数据集一致
y = pd.Series(boston.target, name="MEDV")

2. 数据探索与可视化（EDA）

2.1 EDA相关方法介绍

数据探索与可视化（Exploratory Data Analysis, EDA）是机器学习流程中的关键步骤，用于理解数据分布、特征关系和异常值等。以下是常用方法：

方法 功能 适用场景
pd.DataFrame.head(n) 查看前n行数据 快速了解数据结构和数值格式
pd.DataFrame.info() 显示数据类型、非空值数量 检查缺失值和数据类型合理性
pd.DataFrame.describe() 计算基本统计量（均值、标准差等） 分析数值特征的分布范围
pd.DataFrame.corr() 计算特征间的相关系数 发现特征与目标变量的线性关系
plt.scatter(x, y) 绘制散点图 分析两个变量的相关性（如特征与目标）
sns.histplot(data, kde=True) 绘制直方图+核密度曲线 查看单变量分布（如目标变量分布）
sns.boxplot(x, y) 绘制箱线图 检测异常值和类别特征的分布差异
sns.heatmap(data) 绘制热力图 可视化相关系数矩阵，快速定位强相关特征

2.2 EDA实现步骤及代码

2.2.1 查看前5行数据

在数据分析过程中，首先需要了解数据的基本结构和内容。为了快速掌握数据集的特征，通常会查看数据集的前几行数据。

代码如下所示：

python 复制代码 
# 3.1 数据基本信息查看
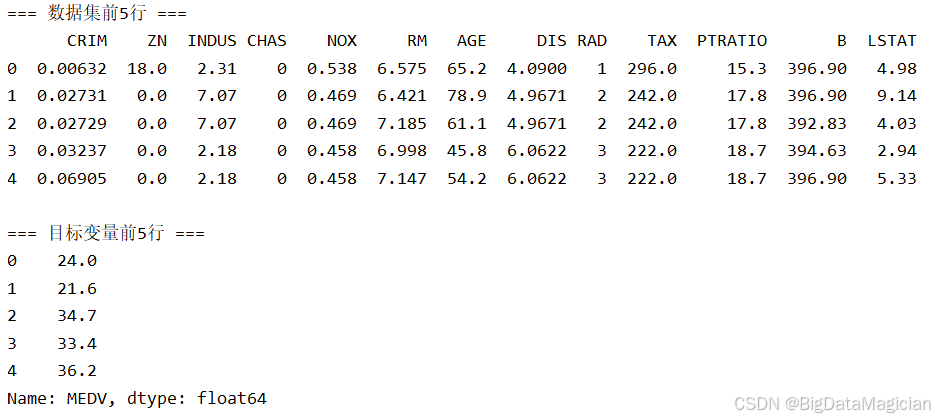
print("\n=== 数据集前5行 ===")
print(X.head())
print("\n=== 目标变量前5行 ===")
print(y.head())

特征变量和目标变量数据前5行如下图所示：

2.2.2 查看数据摘要信息

在数据分析过程中，了解数据集的整体结构和基本统计特征至关重要。通过查看数据的摘要信息，可以快速评估数据的质量并为后续的数据预处理和建模工作提供依据。

代码如下所示：

python 复制代码 
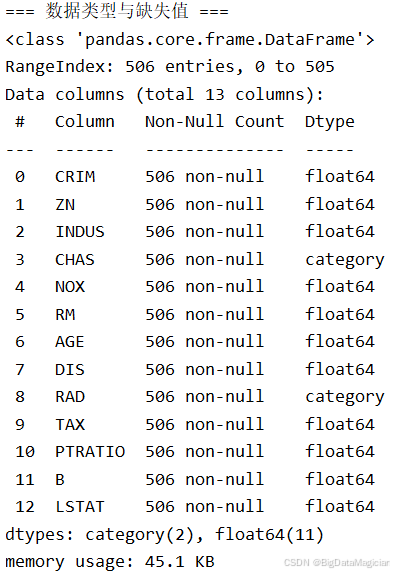
print("\n=== 数据类型与缺失值 ===")
print(X.info())

数据摘要信息如下图所示，该数据集共包含506条记录和13个特征变量，数据类型主要由11个连续型数值变量（float64）和2个分类变量（category）组成，所有变量均无缺失值，数据完整性良好。整体内存占用仅为45.1 KB，结构清晰、质量较高，无需进行缺失值处理，适合直接用于建模分析。其中分类变量CHAS和RAD在后续建模中需进行适当的编码转换，而丰富的数值型特征则有利于回归类模型的训练与分析。

2.2.3 描述性统计分析

在完成数据的基本查看和结构检查后，下一步是对数据进行描述性统计分析，以全面了解各变量的分布特征、集中趋势与离散程度。

代码如下所示：

python 复制代码 
print("\n=== 数值特征统计描述 ===")
print(X.describe())
print("\n=== 目标变量统计描述 ===")
print(y.describe())

描述性统计分析结果如下图所示：


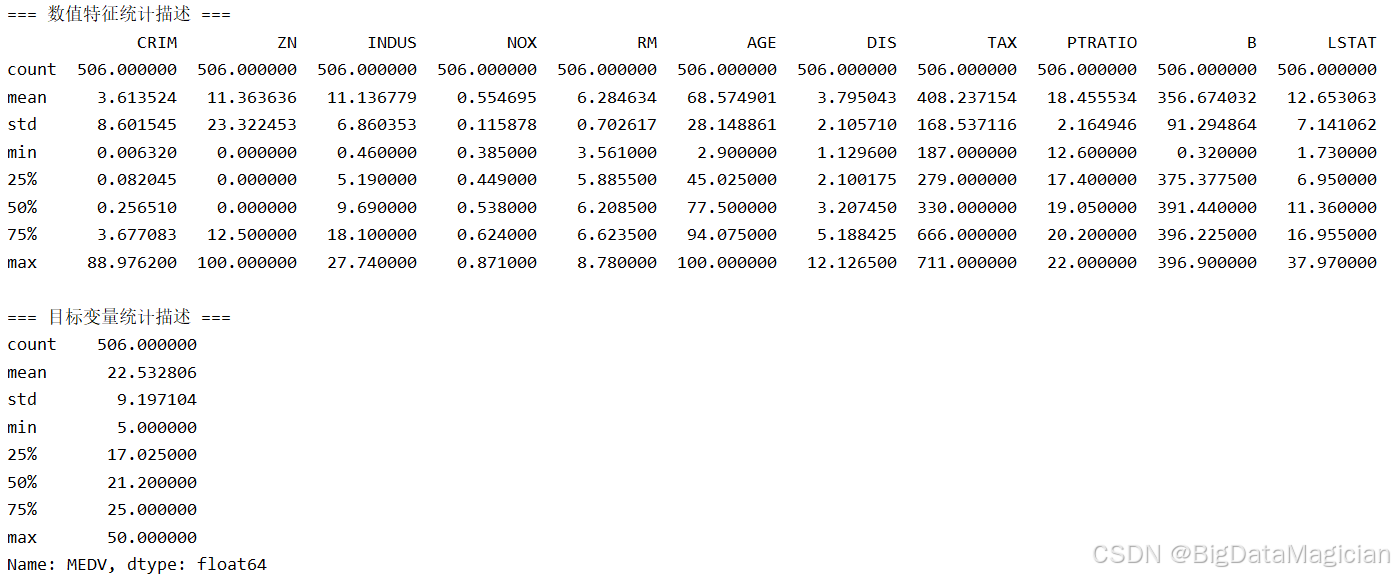
特征变量描述性统计分析结果：

波士顿房价数据集的13个特征变量在数值分布上表现出多样性。多数变量如RM（平均房间数）、NOX（一氧化氮浓度）和PTRATIO（师生比）分布较为集中，标准差较小，说明数据相对稳定；而CRIM（犯罪率）和LSTAT（低收入人群比例）的最大值明显高于均值与75%分位数，可能存在极端值或右偏分布；ZN（住宅用地比例）中位数为0，表明大部分区域几乎没有大型住宅区；AGE（房龄）均值达68.57，显示多数房屋建于较早时期；DIS（距就业中心距离）和TAX（房产税）等变量则呈现出适中的离散程度。整体来看，特征变量涵盖了连续型与分类型数据，量纲差异较大，建议后续进行标准化处理以提升模型性能。

目标变量描述性统计分析结果：

目标变量MEDV（房价中位数）的均值为22.53千美元，中位数为21.2千美元，均值略高于中位数，表明其分布可能轻微右偏；最小值为5千美元，最大值为50千美元，四分位距集中在17.03至25千美元之间，说明大部分区域房价处于中等水平，但存在一定的高房价异常点（上限被截断于50万美元）。标准差约为9.2，反映出不同区域房价差异较为显著。总体来看，MEDV具备合理的变异性，适合作为回归模型的预测目标，但在建模前建议结合可视化手段进一步识别潜在异常值并考虑是否进行变换（如对数转换）以改善分布形态。

2.2.4 目标变量分布分析

代码如下所示：

python 复制代码 
# 3.2 目标变量分布分析
plt.figure(figsize=(10, 6))
# 绘制目标变量（房价）的直方图和核密度曲线
plt.hist(y, bins=30, density=True, alpha=0.7, color='skyblue', edgecolor='black')
y.plot(kind='kde', color='red', linewidth=2)  # 核密度估计曲线
plt.title('Distribution of Boston Housing Prices (MEDV)', fontsize=14)
plt.xlabel('Median Value ($1000s)', fontsize=12)
plt.ylabel('Density', fontsize=12)
plt.grid(alpha=0.3)
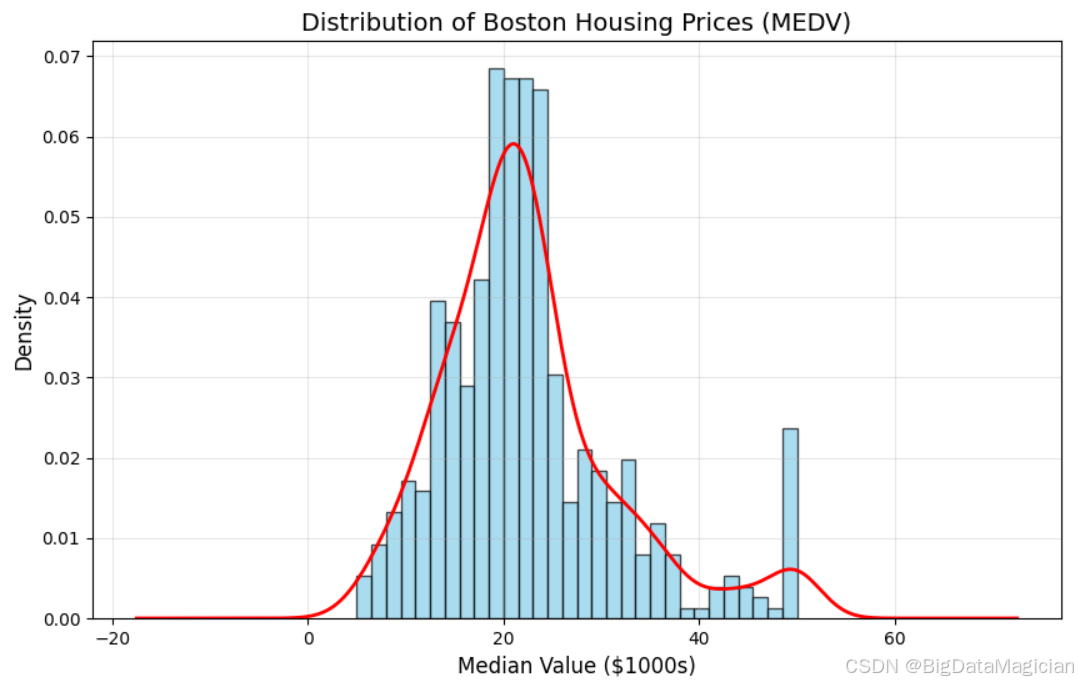
plt.show()

在进行线性回归分析之前，首先对目标变量 MEDV（房价中位数）的分布进行了可视化分析。通过绘制密度直方图和核密度估计曲线，如下图所示，发现 MEDV 的分布呈现出右偏特性，数据集中在15到30千美元之间，且存在少量高价位的异常值，表明大多数住宅价格位于这一区间内，而高价住宅则较少。此外，在40千美元以上出现了一个次峰，可能代表了高端住宅区的存在。

鉴于目标变量 MEDV 的非正态分布特征及存在的偏态和潜在异常值情况，在进行线性回归分析时需采取适当的预处理措施。建议考虑对 MEDV 进行对数变换以改善其分布形态，使其更接近正态分布，从而更好地满足线性回归模型的基本假设。同时，考虑到模型对异常值的敏感性，可以采用鲁棒性更强的回归算法或结合残差诊断来验证模型的拟合效果，确保模型的有效性和可靠性。如果选择继续使用普通线性回归模型，则应特别注意检查和处理这些偏离的数据点，以减少它们对模型预测性能的影响。

2.2.5 目标变量与各个特征变量的相关性分析

为了探究各特征变量对房价中位数（MEDV）的影响程度，本节进行了相关性分析，计算了目标变量 MEDV 与13个特征变量之间的皮尔逊相关系数。相关系数的取值范围为 [-1, 1]，其绝对值越大表示线性关系越强，正负号表示方向：正值代表正相关，负值代表负相关。实现代码如下所示：

python 复制代码 
# 3.3 特征与目标变量的相关性分析
# 计算所有特征与目标变量的相关系数
df_X = X.copy()
df_X['CHAS'] = df_X['CHAS'].astype(float)
df_X['RAD'] = df_X['RAD'].astype(float)
correlations = df_X.corrwith(y).sort_values(ascending=False)
print("\n=== 特征与目标变量（MEDV）的相关系数 ===")
print(correlations)

# 可视化相关性（条形图）
plt.figure(figsize=(12, 6))
correlations.plot(kind='bar', color=['green' if x > 0 else 'red' for x in correlations])
plt.title('Correlation Between Features and Housing Prices (MEDV)', fontsize=14)
plt.axhline(y=0, color='black', linestyle='--', alpha=0.3)  # 添加水平线（y=0）
plt.xlabel('Features', fontsize=12)
plt.ylabel('Correlation Coefficient', fontsize=12)
plt.grid(axis='y', alpha=0.3)
plt.xticks(rotation=45, ha='right')  # 旋转x轴标签，避免重叠
plt.show()

目标变量与各个特征变量的相关性如下图所示：

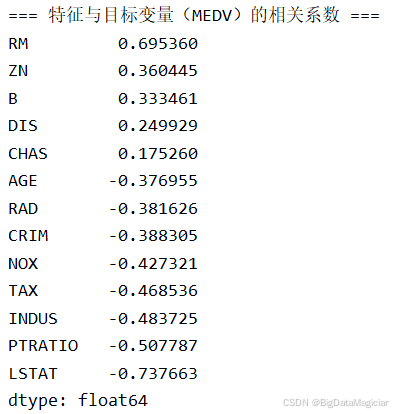
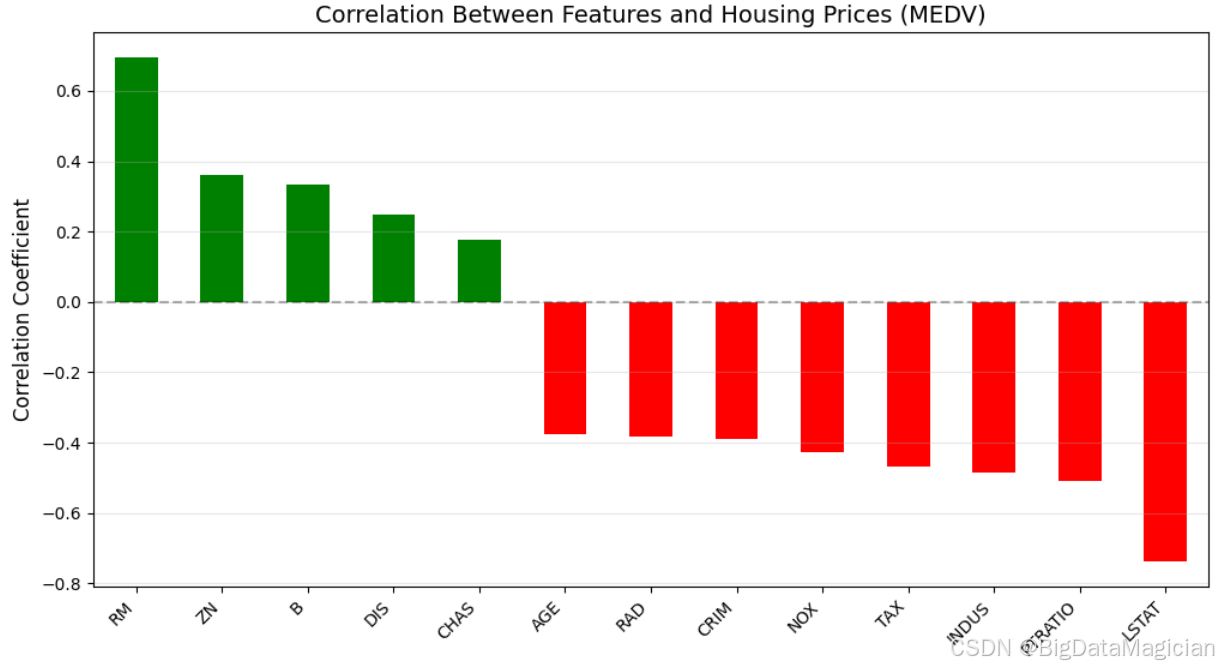
为了更直观地展示目标变量 MEDV（房价中位数）与各特征变量之间的线性关系强度和方向，对相关系数进行了可视化分析，绘制了柱状图以呈现每个特征变量与 MEDV 的皮尔逊相关系数。目标变量与各个特征变量的相关性可视化结果如下图所示，通过相关性可视化可以直观看出，RM 和 LSTAT 是影响房价最显著的两个变量，分别具有最强的正向和负向线性关系。其他变量如 PTRATIO、TAX、NOX 等也具有较强的解释能力，而部分变量如 ZN、CHAS 虽有一定相关性但较弱。这为后续建模提供了重要指导：可优先选择高相关性变量作为核心预测因子，并考虑剔除相关性极低的变量以简化模型。同时需注意，相关性不代表因果关系，且仅反映线性关联，建议结合散点图等方法进一步验证变量间的真实关系。

2.2.6 验证变量间的真实关系

在完成相关性分析后，仅依赖相关系数可能无法全面反映变量之间的实际关系。为了更深入地理解目标变量 MEDV（房价中位数）与关键特征变量之间的真实关联模式，可通过绘制散点图并叠加线性趋势线，对相关性最强的两个正相关和两个负相关特征进行可视化验证。实现代码如下所示：

python 复制代码 
# 3.4 强相关特征与目标变量的散点图
# 选择与目标变量相关性最强的2个正相关和2个负相关特征
top_positive = correlations.index[:2]  # 前2个正相关特征
top_negative = correlations.index[-2:]  # 最后2个负相关特征
selected_features = list(top_positive) + list(top_negative)

plt.figure(figsize=(15, 10))
for i, feature in enumerate(selected_features, 1):
    plt.subplot(2, 2, i)
    plt.scatter(X[feature], y, alpha=0.6, color='purple', edgecolor='white', s=30)
    # 添加趋势线（线性拟合）
    z = np.polyfit(X[feature], y, 1)
    p = np.poly1d(z)
    plt.plot(X[feature], p(X[feature]), "r--")
    plt.title(f'{feature} vs MEDV (Corr: {correlations[feature]:.2f})', fontsize=12)
    plt.xlabel(feature, fontsize=10)
    plt.ylabel('MEDV ($1000s)', fontsize=10)
    plt.grid(alpha=0.3)

plt.tight_layout()  # 调整子图间距
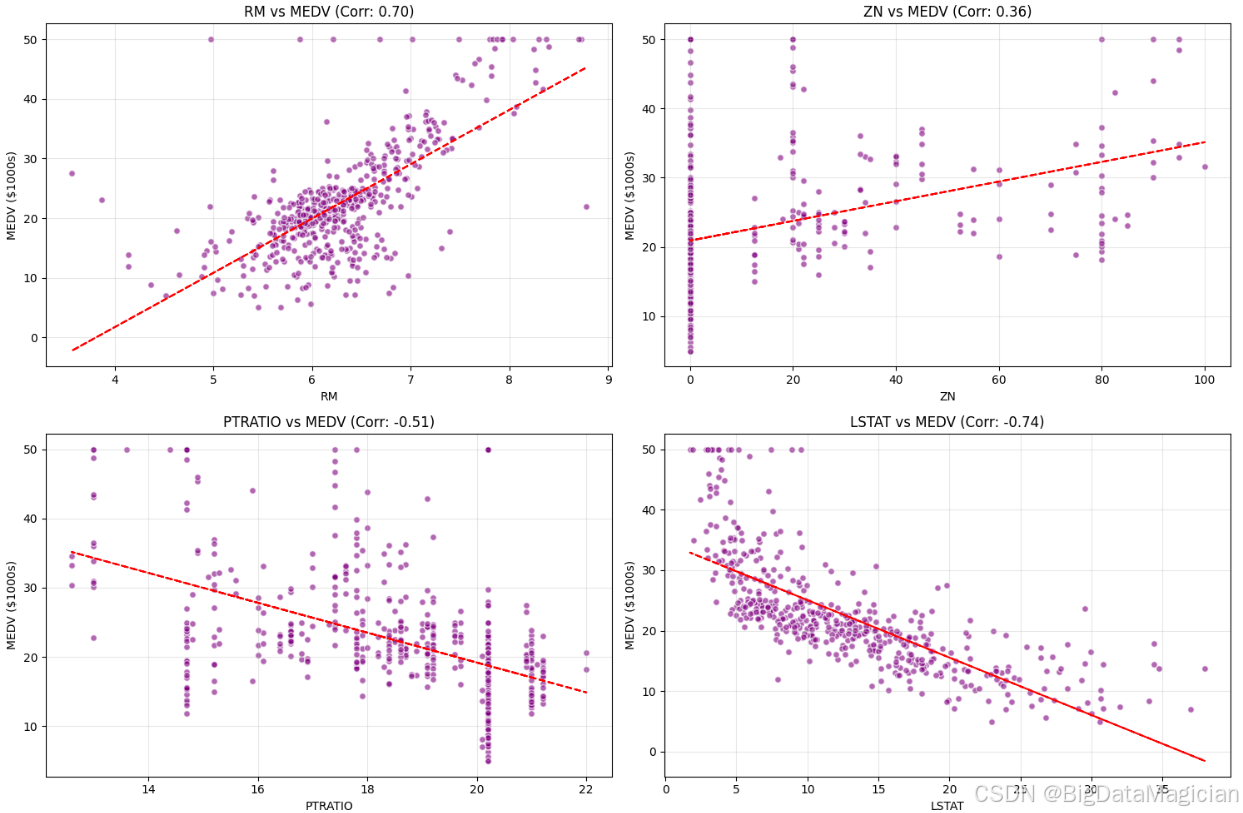
plt.show()

特征变量与目标变量相关性最强的2个正相关和2个负相关可视化结果如下图所示，从图中可以看出 RM 和 LSTAT 不仅在统计上具有强相关性，在图形上也表现出清晰的线性关系，适合作为线性回归模型的核心输入变量；ZN 和 PTRATIO 虽相关性较低或中等，但仍存在可识别的趋势，可用于辅助建模；所有变量均未显示出明显的非线性结构（如曲线、分段等），说明使用线性模型进行初步建模是合理的；数据中存在少量离群点（如 RM 较高但 MEDV 较低的情况），建议在后续建模时考虑鲁棒性方法或异常值处理策略。

2.2.7 特征间的相关性分析

多重共线性指的是自变量（特征变量）之间存在高度线性相关关系的现象，会导致模型（函数）难以区分它们各自对目标变量的独立贡献。这种现象会影响模型的稳定性、解释性和预测能力。

在构建回归模型时，除了关注特征与目标变量之间的关系外，还需考察特征变量之间的相互关联性 。若某些特征之间存在高度相关性（多重共线性） ，可能导致模型参数估计不稳定、解释能力下降或过拟合等问题。因此，通过绘制特征间相关系数热力图，全面分析各特征变量之间的线性相关关系。实现代码如下所示：

python 复制代码 
# 3.5 特征间的相关性热力图
plt.figure(figsize=(14, 10))
# 计算所有特征间的相关系数矩阵
corr_matrix = X.corr()
# 绘制热力图
import seaborn as sns

sns.heatmap(corr_matrix, annot=True, fmt=".2f", cmap='coolwarm',
            square=True, linewidths=0.5, cbar_kws={"shrink": .8})
plt.title('Correlation Matrix of Features', fontsize=14)
plt.xticks(rotation=45, ha='right')
plt.yticks(rotation=0)
plt.show()

特征间的相关性热力图如下图所示，从图中可以观察到以下关键点：

  • NOX 与 DIS ：相关系数为 -0.77，呈强负相关，表明距离就业中心越远（DIS越大），一氧化氮浓度越低（NOX越小），符合环境地理规律；
  • INDUS 与 NOX ：相关系数为 0.76，强正相关，说明工业用地比例越高，空气污染程度也越高；
  • RAD 与 TAX ：相关系数高达 0.91，属于极强正相关，意味着靠近放射状公路的区域通常税率也较高，可能存在空间集聚效应；
  • DIS 与 AGE ：相关系数为 0.73，表明较老的房屋多分布在远离市中心的区域；
  • CRIM 与 RAD ：相关系数为 0.63，说明高犯罪率区域往往集中在交通便利但可能管理较差的地区；
  • RM 与 LSTAT ：相关系数为 -0.61，负相关较强，即房间越多的住宅区，低收入人群比例越低，反映了居住品质与社会经济水平的关联；
  • 多数其他变量之间的相关性较低（如 |r| < 0.4），说明整体上特征独立性较好。

此外，对角线上的值均为1.00，代表每个变量与自身的完全相关；颜色分布均衡，未出现大量极端值，表明数据结构较为合理。

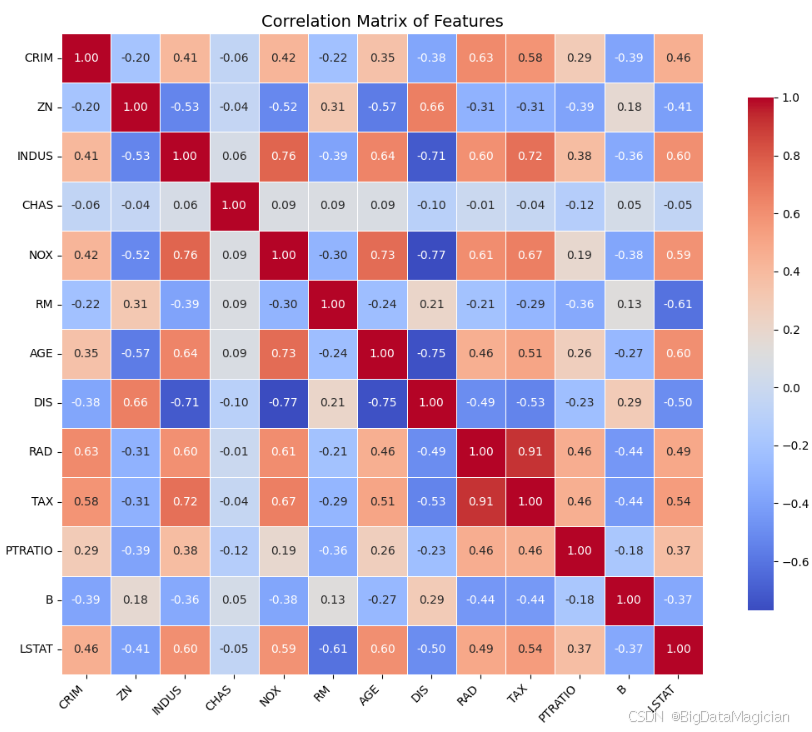
通过特征间相关性热力图分析可知：

  • 数据中存在若干强相关变量对 ，如 RAD-TAX、INDUS-NOX、NOX-DIS 等，这些组合提示可能存在冗余信息或共同驱动因素；
  • 特别是 RAD 和 TAX 的相关系数高达 0.91，已接近多重共线性的警戒线（一般认为 > 0.8 需警惕），在建模时应避免同时使用这两个变量，或采用主成分分析（PCA）、岭回归等方法缓解共线性问题；
  • 其他变量之间的相关性普遍较弱，说明大多数特征提供了相对独立的信息，有利于模型的稳定性和泛化能力；
  • 建议在后续建模过程中结合方差膨胀因子（VIF） 进一步量化多重共线性影响，并根据业务逻辑选择最具代表性的变量进行建模。

2.3 EDA 完整代码

python 复制代码 
# 3. 数据探索与可视化（EDA）

# 3.1 数据基本信息查看
print("\n=== 数据集前5行 ===")
print(X.head())  # 查看特征数据前5行
print("\n=== 目标变量前5行 ===")
print(y.head())  # 查看目标变量前5行

print("\n=== 数据类型与缺失值 ===")
print(X.info())  # 检查特征数据类型和非空值数量

print("\n=== 数值特征统计描述 ===")
print(X.describe())  # 计算特征的均值、标准差、分位数等
print("\n=== 目标变量统计描述 ===")
print(y.describe())  # 目标变量的统计信息

# 3.2 目标变量分布分析
plt.figure(figsize=(10, 6))
# 绘制目标变量（房价）的直方图和核密度曲线
plt.hist(y, bins=30, density=True, alpha=0.7, color='skyblue', edgecolor='black')
y.plot(kind='kde', color='red', linewidth=2)  # 核密度估计曲线
plt.title('Distribution of Boston Housing Prices (MEDV)', fontsize=14)
plt.xlabel('Median Value ($1000s)', fontsize=12)
plt.ylabel('Density', fontsize=12)
plt.grid(alpha=0.3)
plt.show()

# 3.3 特征与目标变量的相关性分析
# 计算所有特征与目标变量的相关系数
df_X = X.copy()
df_X['CHAS'] = df_X['CHAS'].astype(float)
df_X['RAD'] = df_X['RAD'].astype(float)
correlations = df_X.corrwith(y).sort_values(ascending=False)
print("\n=== 特征与目标变量（MEDV）的相关系数 ===")
print(correlations)

# 可视化相关性（条形图）
plt.figure(figsize=(12, 6))
correlations.plot(kind='bar', color=['green' if x > 0 else 'red' for x in correlations])
plt.title('Correlation Between Features and Housing Prices (MEDV)', fontsize=14)
plt.axhline(y=0, color='black', linestyle='--', alpha=0.3)  # 添加水平线（y=0）
plt.xlabel('Features', fontsize=12)
plt.ylabel('Correlation Coefficient', fontsize=12)
plt.grid(axis='y', alpha=0.3)
plt.xticks(rotation=45, ha='right')  # 旋转x轴标签，避免重叠
plt.show()

# 3.4 强相关特征与目标变量的散点图
# 选择与目标变量相关性最强的2个正相关和2个负相关特征
top_positive = correlations.index[:2]  # 前2个正相关特征
top_negative = correlations.index[-2:]  # 最后2个负相关特征
selected_features = list(top_positive) + list(top_negative)

plt.figure(figsize=(15, 10))
for i, feature in enumerate(selected_features, 1):
    plt.subplot(2, 2, i)
    plt.scatter(X[feature], y, alpha=0.6, color='purple', edgecolor='white', s=30)
    # 添加趋势线（线性拟合）
    z = np.polyfit(X[feature], y, 1)
    p = np.poly1d(z)
    plt.plot(X[feature], p(X[feature]), "r--")
    plt.title(f'{feature} vs MEDV (Corr: {correlations[feature]:.2f})', fontsize=12)
    plt.xlabel(feature, fontsize=10)
    plt.ylabel('MEDV ($1000s)', fontsize=10)
    plt.grid(alpha=0.3)

plt.tight_layout()  # 调整子图间距
plt.show()

# 3.5 特征间的相关性热力图
plt.figure(figsize=(14, 10))
# 计算所有特征间的相关系数矩阵
corr_matrix = X.corr()
# 绘制热力图
import seaborn as sns

sns.heatmap(corr_matrix, annot=True, fmt=".2f", cmap='coolwarm',
            square=True, linewidths=0.5, cbar_kws={"shrink": .8})
plt.title('Correlation Matrix of Features', fontsize=14)
plt.xticks(rotation=45, ha='right')
plt.yticks(rotation=0)
plt.show()

代码说明：

  1. 基本信息查看 ：通过head()、info()和describe()快速掌握数据结构、缺失值和统计分布。
  2. 目标变量分布：直方图+核密度曲线展示房价（MEDV）的分布形态，判断是否近似正态分布。
  3. 单特征相关性 ：通过相关系数和条形图，定位对房价影响最强的特征（如LSTAT负相关、RM正相关）。
  4. 散点图分析：对强相关特征绘制散点图并添加趋势线，直观展示线性关系强度。
  5. 特征间相关性 ：热力图用于检测多重共线性（如TAX与RAD强相关），为特征选择提供依据。

通过以上分析，可初步确定关键特征（如RM、LSTAT）对房价的影响，为后续建模提供方向。

3. 数据预处理

数据预处理是建模前的关键步骤，直接影响模型性能。

3.1 处理缺失值

波士顿房价数据集通常无缺失值，但实际场景中需常规检查和处理。

3.2 特征选择

3.2.1 特征选择相关方法

（1）variance_inflation_factor 方法介绍
variance_inflation_factor 是 statsmodels 库中用于检测多重共线性 的核心函数，其作用是计算每个特征的方差膨胀因子（VIF）。

多重共线性：指特征之间存在强线性相关关系（例如"房屋面积"和"房间数"高度相关），会导致回归模型系数不稳定、解释性下降。

VIF值含义：衡量某个特征被其他特征线性解释的程度，VIF值越大，说明该特征与其他特征的共线性越强。

通常认为 VIF < 5 表示共线性较弱；5 ≤ VIF ≤ 10 表示存在中等共线性；VIF > 10 表示存在强共线性（需要剔除）。

（2）variance_inflation_factor 参数说明

参数名称 数据类型 作用说明 示例值
exog 二维数组/矩阵 输入的特征矩阵（包含多个特征），要求特征已转换为数值型，且无缺失值。 X.values（假设 X 是包含筛选后特征的DataFrame）
exog_idx 整数 指定需要计算VIF值的特征索引（即特征在 exog 矩阵中的列位置）。 0（计算第1列特征的VIF）、2（计算第3列特征的VIF）
3.2.2 特征选择：基于相关性与多重共线性分析的优化筛选

在构建线性回归模型前，合理的特征选择不仅能提升模型性能，还能增强其可解释性和稳定性。结合相关性分析 与方差膨胀因子（VIF） 方法，对原始特征进行两阶段筛选：首先根据与目标变量的相关系数选取强相关特征，再通过 VIF 检测并剔除存在严重多重共线性的变量，从而获得一组既具有预测能力又相互独立的最优特征子集。

  1. 第一阶段：基于相关系数筛选

    设定阈值 |corr| > 0.5，从所有特征中选出与目标变量 MEDV 相关性较强的变量。结果显示：

    • RM（平均房间数）：相关系数为 0.695，正向影响显著；
    • PTRATIO（师生比）：相关系数为 -0.508，负向影响较强；
    • LSTAT（低收入人群比例）：相关系数为 -0.738，是影响最强的负相关变量。

    因此，初步筛选出三个特征：['RM', 'PTRATIO', 'LSTAT']。

  2. 第二阶段：VIF 分析剔除多重共线性

    使用 statsmodels 计算各特征的 VIF 值，用于衡量多重共线性程度。初始 VIF 结果如下：

    • PTRATIO: VIF = 51.797 → 极高，表明其与其他变量高度相关；
    • RM: VIF = 36.068 → 也远高于警戒值（通常认为 VIF > 10 即存在严重共线性）；
    • LSTAT: VIF = 5.855 → 在合理范围内。

    由于 PTRATIO 和 RM 的 VIF 值均远超 10，说明它们之间或与其它变量存在强线性依赖关系。按照策略，优先剔除 VIF 最大的特征------PTRATIO。

    剔除后重新计算 VIF：

    • RM: VIF = 3.253
    • LSTAT: VIF = 3.253
      两者均降至安全范围（< 10），表明剩余特征间已无显著多重共线性问题。

实现代码如下所示：

python 复制代码 
# 方法1：基于相关系数手动筛选（选择绝对值>0.5的特征）
corr_threshold = 0.5
selected_features = correlations[abs(correlations) > corr_threshold].index.tolist()
print(f"\n基于相关系数筛选的特征（|corr| > {corr_threshold}）：{selected_features}")

# 方法2：计算VIF剔除多重共线性特征（可选）
from statsmodels.stats.outliers_influence import variance_inflation_factor

def calculate_vif(X):
    vif_data = pd.DataFrame()
    vif_data["特征"] = X.columns
    vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
    return vif_data.sort_values("VIF", ascending=False)

# 初始VIF计算
vif_df = calculate_vif(X[selected_features])
print("\n初始VIF值：")
print(vif_df)

# 剔除VIF>10的特征（通常认为VIF>10存在强共线性）
while vif_df["VIF"].max() > 10:
    # 删除VIF最大的特征
    drop_feature = vif_df.iloc[0]["特征"]
    selected_features.remove(drop_feature)
    vif_df = calculate_vif(X[selected_features])
    print(f"\n剔除特征 {drop_feature} 后VIF值：")
    print(vif_df)

# 更新特征矩阵
X_selected = X[selected_features]
print(f"\n最终筛选后的特征：{selected_features}")

打印结果如下图所示：

经过两步筛选流程，最终保留的特征为：['RM', 'LSTAT']。这两个变量不仅与房价有很强的线性关系（分别对应正负方向），而且彼此之间的共线性较低，能够有效避免模型参数估计不稳定的问题。

3.3 数据标准化（归一化）

3.3.1 数据标准化相关方法

（1） 常用数据标准化方法

方法类名称 功能说明 适用场景
StandardScaler 标准化为均值=0，标准差=1 （Z-score标准化）： x' = (x - μ) / σ，其中μ为均值，σ为标准差 适用于特征值近似正态分布的场景，保留异常值的影响（如线性回归、SVM等），能有效消除量纲影响
MinMaxScaler 归一化为 [0, 1]区间 ： x' = (x - x_min) / (x_max - x_min) 适用于特征值分布未知或有边界的场景（如神经网络输入），但对异常值敏感
RobustScaler 基于中位数和四分位距标准化，抗异常值： x' = (x - median) / (Q3 - Q1) 适用于存在较多异常值的场景，减少极端值对标准化结果的影响
Normalizer 对样本进行归一化（L1/L2范数），使每个样本的特征向量模长为1 适用于关注样本间距离的场景（如文本分类、KNN），强调样本内部特征的相对占比

（2）fit_transform方法（核心预处理方法）

所有标准化类都继承了TransformerMixin，因此都包含fit_transform方法，其作用是先拟合数据（计算标准化所需参数，如均值、标准差），再对数据进行转换 ，是fit和transform方法的合并操作，效率更高。

fit_transform方法参数说明（以StandardScaler为例，其他类参数类似）

参数名称 数据类型 默认值 作用说明
X 数组/矩阵（2D） 无 输入的特征数据（形状为[n_samples, n_features]），需为数值型
y 数组/None None 目标变量（大多数标准化方法不需要，仅为兼容sklearn的API接口保留）
sample_weight 数组/None None 样本权重（可选），用于加权计算均值/标准差（仅部分类支持，如StandardScaler）

（3）fit与transform的区别

  • fit(X) ：仅计算标准化所需的参数（如StandardScaler会计算X的均值μ和标准差σ），不改变输入数据。
  • transform(X) ：使用fit计算的参数对X进行标准化转换（如应用(x - μ) / σ），但需先调用fit或直接使用fit_transform。
3.3.2 数据标准化

在构建线性回归模型时，由于不同特征的量纲和数值范围差异较大（如 RM 的取值在 4~9 之间，而 LSTAT 在 1~38 之间），若不进行处理，模型会偏向于数值较大的变量，导致权重分配失衡。因此，数据标准化 是必要的预处理步骤，旨在将各特征缩放到统一尺度，消除量纲的影响，使它们在模型训练中具有可比性和公平性。

本案例选择使用 StandardScaler 进行标准化，因为它更适合处理连续型数值变量且能较好地保持数据的统计特性。

实现代码如下所示：

python 复制代码 
from sklearn.preprocessing import StandardScaler

# 初始化标准化器
scaler = StandardScaler()

# 对筛选后的特征进行标准化
X_scaled = scaler.fit_transform(X_selected)

# 转换为DataFrame便于查看
X_scaled_df = pd.DataFrame(X_scaled, columns=selected_features)
print("\n标准化后的特征前5行：")
print(X_scaled_df.head())
print("\n标准化后特征的均值和标准差：")
print(pd.DataFrame({
    "均值": X_scaled_df.mean().round(4),
    "标准差": X_scaled_df.std().round(4)
}))

标准化后的特征前5行数据和标准化后特征的均值和标准差为如下图所示，从图中可以看出经过 StandardScaler 处理后，两个特征 RM 和 LSTAT 的均值均接近于 0 ，标准差均约为 1，满足标准化要求；数值范围已调整至以 0 为中心、单位方差的分布，消除了原始量纲差异的影响；每个样本的特征值现在可以公平地参与模型参数学习，避免因尺度问题导致的偏差。

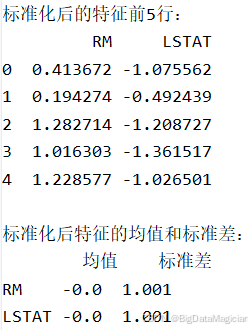
通过数据标准化处理，成功将 RM 和 LSTAT 两个特征转换为同一尺度下的标准化变量，显著提升了后续线性回归模型的稳定性和收敛效率。

在实际建模中，应始终在训练集上拟合标准化器（即调用 .fit_transform()），并在测试集或新数据上仅使用相同的变换规则（即调用 .transform()），以保证数据一致性，避免数据泄露。

3.4 划分训练集与测试集

3.4.1 相关方法说明
方法 功能 参数说明
train_test_split() 随机划分数据集 test_size：测试集比例（通常为0.2~0.3） random_state：设置随机种子以保证结果可复现 shuffle：是否打乱原始数据顺序（默认为True）
3.4.2 划分训练集与测试集代码实现

在机器学习建模流程中，将数据划分为训练集 和测试集 是评估模型泛化能力的关键步骤。训练集用于拟合模型参数，而测试集则用于独立验证模型在未见数据上的表现，避免过拟合问题。合理的划分方式能有效反映模型的真实性能。本案例使用 sklearn.model_selection.train_test_split() 函数进行划分，选择 20% 的数据作为测试集 ，其余 80% 用于训练，并设定 random_state=42 确保实验结果可重复。

实现代码如下所示：

python 复制代码 
# 划分训练集和测试集（测试集占20%）
X_train, X_test, y_train, y_test = train_test_split(
    X_scaled,  # 标准化后的特征
    y.values,  # 目标变量（转为数组）
    test_size=0.2,  # 测试集比例
    random_state=42  # 随机种子，保证结果可复现
)

# 查看划分后的数据形状
print(f"\n训练集特征形状：{X_train.shape}，测试集特征形状：{X_test.shape}")
print(f"训练集目标形状：{y_train.shape}，测试集目标形状：{y_test.shape}")

运行结果如下图所示，原始数据共 506 条样本，按 8:2 比例划分后，训练集包含 404 个样本 ，测试集包含 102 个样本 ；特征维度为 2（即 RM 和 LSTAT），因此训练集和测试集的特征矩阵均为 (n_samples, 2)；目标变量为一维数组，形状分别为 (404,) 和 (102,)，符合回归任务要求；数据已通过 shuffle=True 打乱顺序，确保划分过程无偏，提升模型评估的可靠性。

本次数据划分合理且具有代表性，既保证了足够的训练样本用于模型学习，又保留了足够数量的测试样本用于性能评估。通过设定固定的随机种子，实现了实验结果的可复现性，便于后续对比不同模型或参数调整的效果。

3.5 预处理总结

  1. 缺失值处理：波士顿数据集无缺失值，实际场景可采用均值/中位数填充；
  2. 特征选择：结合相关系数和VIF剔除弱相关和高共线性特征，保留核心变量；
  3. 标准化 ：使用StandardScaler消除量纲影响，使模型更稳定；
  4. 数据集划分：按8:2比例拆分训练集和测试集，确保模型评估的客观性。

预处理后的数据集可直接用于线性回归模型训练。

4. 构建线性回归模型

线性回归是一种经典且易于解释的监督学习算法，适用于预测连续型目标变量。其核心思想是通过拟合一个线性方程来建立特征与目标之间的关系，数学表达式为：

y ^ = w 0 + w 1 x 1 + w 2 x 2 + ⋯ + w n x n \hat{y} = w_0 + w_1x_1 + w_2x_2 + \cdots + w_nx_n y^=w0+w1x1+w2x2+⋯+wnxn

其中， y ^ \hat{y} y^ 是预测的房价中位数（MEDV）， w 0 w_0 w0 为截距项， w 1 , w 2 , ... , w n w_1, w_2, \ldots, w_n w1,w2,...,wn 为各特征对应的回归系数，反映每个特征对目标变量的影响强度和方向。

4.1 相关方法说明

在scikit-learn（sklearn）库中，LinearRegression是用于实现普通最小二乘线性回归 的类，通过拟合数据找到最佳线性关系（ y = w 0 + w 1 x 1 + w 2 x 2 + . . . + w n x n y = w₀ + w₁x₁ + w₂x₂ + ... + wₙxₙ y=w0+w1x1+w2x2+...+wnxn），使预测值与真实值的平方误差最小。以下是其构造方法、参数及属性的详细介绍：

4.1.1 LinearRegression构造方法简介

LinearRegression的核心是通过最小化残差平方和求解回归系数，适用于连续型目标变量的线性预测问题（如房价预测、销售额预测等）。其构造方法用于初始化模型参数，语法如下：

python 复制代码 
from sklearn.linear_model import LinearRegression

model = LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=None, positive=False)
4.1.2 LinearRegression构造方法参数说明
参数名称 数据类型 默认值 作用说明
fit_intercept bool True 是否计算模型的截距项（ w 0 w₀ w0）。 - True：模型包含截距项（默认）； - False：假设数据已中心化（截距项为0）。
copy_X bool True 是否复制输入特征数据（X）。 - True：不修改原始数据（默认）； - False：可能修改原始数据以节省内存。
n_jobs int/None None 用于计算的CPU核心数（仅在fit时有效）。 - None：使用1个核心（默认）； - -1：使用所有可用核心。
positive bool False 是否强制回归系数（ w 1 , w 2 , . . . , w n w₁, w₂, ..., wₙ w1,w2,...,wn）为非负数。 - True：系数只能≥0（适用于物理意义上非负的场景，如销量、价格）； - False：系数可正可负（默认）。
4.1.3 LinearRegression的核心属性（模型训练后可用）
属性名称 数据类型 含义说明
coef_ 数组（1D） 模型的回归系数（ w 1 , w 2 , . . . , w n w₁, w₂, ..., wₙ w1,w2,...,wn），顺序与输入特征的列顺序一致。
intercept_ 浮点数 模型的截距项（ w 0 w₀ w0），仅当fit_intercept=True时有效。
rank_ int 特征矩阵X的秩（反映特征的线性独立性）。
singular_ 数组（1D） 特征矩阵X的奇异值（用于评估矩阵的稳定性）。
n_features_in_ int 训练时输入的特征数量。
feature_names_in_ 数组（1D） 训练时输入的特征名称（仅当输入X为DataFrame时可用）。

在scikit-learn中，LinearRegression构造方法返回的是一个线性回归模型对象（LinearRegression实例），该对象包含模型训练、预测、评估 等核心方法，以及训练后可访问的模型参数属性。以下是其方法、参数及属性的详细介绍：

4.1.4 LinearRegression对象的核心方法

这些方法用于模型训练、预测及其他操作，是使用线性回归模型的核心接口。

方法名称 功能说明 参数列表及说明 返回值
fit(X, y) 训练模型：根据输入特征X和目标变量y，求解回归系数（最小化残差平方和），残差 = 实际值 - 预测值（ e i = y i − y ^ i e_i = y_i - \hat{y}_i ei=yi−y^i），绝对误差是残差的绝对值。 - X：特征数据（数组/矩阵，形状为[n_samples, n_features]，必须为数值型） - y：目标变量（数组，形状为[n_samples]或[n_samples, n_targets]） - sample_weight（可选）：样本权重数组（形状为[n_samples]），用于加权最小二乘 模型对象本身（self），支持链式调用
predict(X) 预测：使用训练好的模型对新特征数据X进行预测。 - X：待预测的特征数据（形状需与训练时的X一致，即[n_samples, n_features]） 预测结果数组（形状为[n_samples]或[n_samples, n_targets]）
score(X, y) 评估：计算模型在X和y上的决定系数（R²），衡量模型拟合优度。 - X：特征数据（同predict） - y：真实目标变量（同fit） - sample_weight（可选）：样本权重数组 R²值（浮点数，范围通常为(-∞, 1]，越接近1表示拟合越好）
get_params(deep=True) 获取模型当前的参数配置（如fit_intercept、positive等）。 - deep：是否递归获取嵌套参数（默认True） 参数字典（键为参数名，值为对应参数值）
set_params(**params) 修改模型参数（需在训练前调用）。 - ** params：关键字参数，如fit_intercept=False、positive=True等 模型对象本身（更新参数后）

4.2 构建线性回归模型代码实现

实现代码如下所示：

python 复制代码 
from sklearn.linear_model import LinearRegression

# 初始化线性回归模型
lr_model = LinearRegression(fit_intercept=True)

# 使用训练集训练模型
lr_model.fit(X_train, y_train)

# 输出模型参数
print("=== 线性回归模型参数 ===")
print(f"截距项（w0）：{lr_model.intercept_:.4f}")
print("特征系数（w1...wn）：")
for feature, coef in zip(selected_features, lr_model.coef_):
    print(f"  {feature}: {coef:.4f}")

运行结果如下图所示，截距项（ w 0 w₀ w0）= 22.5019 ：表示当 RM = 0 且 LSTAT = 0 时，模型预测的房价为约 22.5 万美元。虽然现实中不可能存在房间数为零的情况，但该值是数学上的基准点。RM 的系数（ w 1 w₁ w1）= 3.8361 ：为正值，说明平均房间数每增加一个单位（标准化后），房价中位数将上升约 3.84 千美元（在原始尺度下需结合标准化逆变换理解）。这表明房屋规模越大，价格越高，符合经济逻辑。LSTAT 的系数（ w 2 w₂ w2）= -4.5122：为负值，说明低收入人群比例每上升一个单位（标准化后），房价下降约 4.51 千美元。这反映出社区社会经济水平对房价有显著抑制作用。

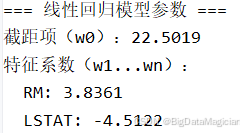
本模型成功建立了基于 RM 和 LSTAT 的线性预测关系，两个特征均表现出强而明确的统计意义。模型结构简洁、可解释性强，能够清晰地揭示出房屋品质 （RM）和社区社会经济状况（LSTAT）对房价的核心驱动作用。下一步将利用测试集评估模型的泛化能力，并进一步优化性能。

5. 模型预测

5.1 模型预测相关方法

方法 功能 输出格式
model.predict(X) 对输入特征矩阵X生成预测值 与X行数相同的一维数组

5.2 模型预测代码实现

在完成模型训练后，下一步是使用训练好的线性回归模型对测试集进行预测，以评估其在未见过的数据上的泛化能力。通过比较预测值与真实值之间的差异，可以直观地了解模型的预测精度和稳定性。

实现代码如下所示：

python 复制代码 
# 对训练集和测试集进行预测
y_train_pred = lr_model.predict(X_train)  # 训练集预测值
y_test_pred = lr_model.predict(X_test)    # 测试集预测值

# 查看部分预测结果
print("\n=== 预测结果示例（前5条） ===")
comparison = pd.DataFrame({
    "真实值": y_test,
    "预测值": y_test_pred,
    "误差": (y_test_pred - y_test).round(2)
})
comparison.to_csv("线性回归预测结果.csv", index=False)
print(comparison)

运行结果的部分数据如下图所示，从误差分布来看，多数预测值接近真实值，但存在一定的系统性偏差，这可能与数据分布或模型假设有关。

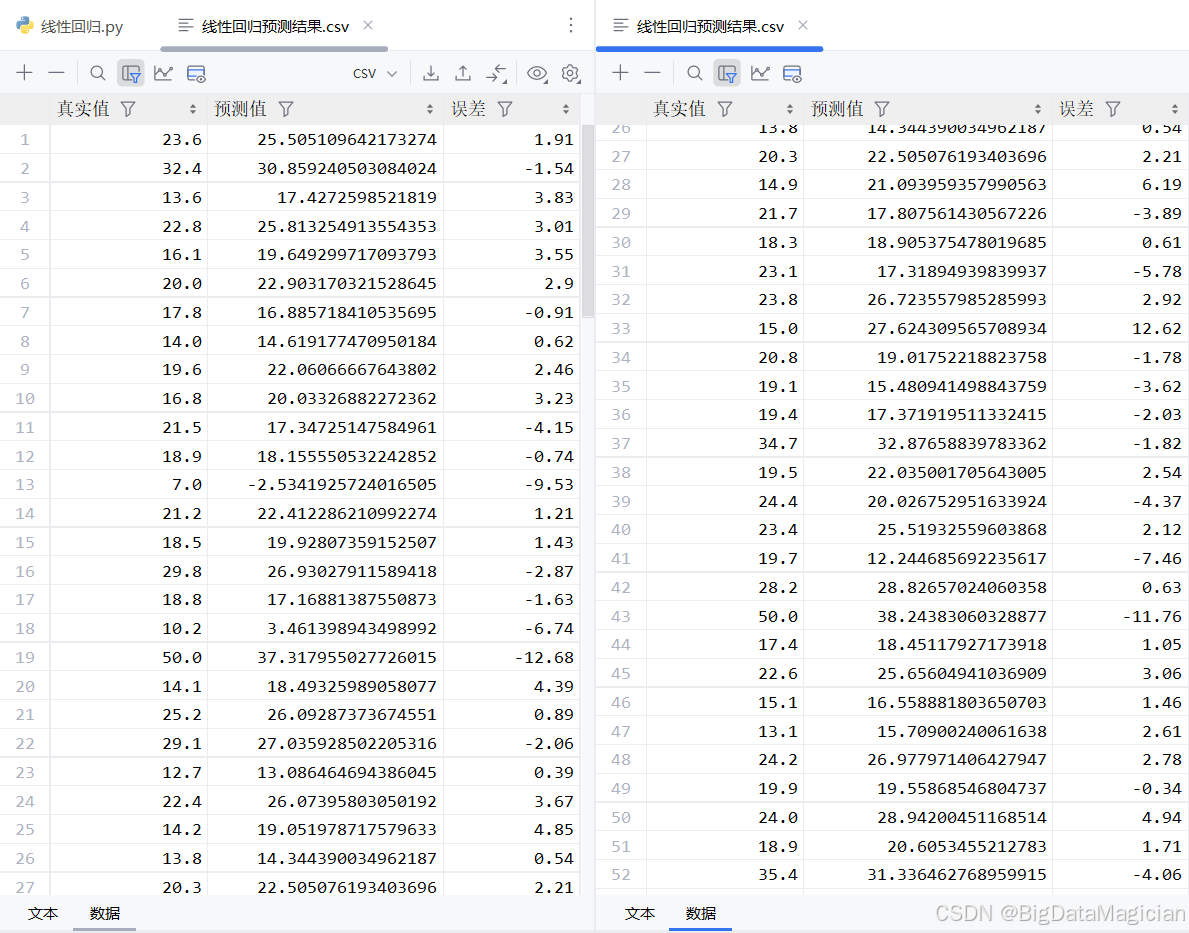
该线性回归模型在测试集上具备一定的预测能力，能够较为准确地捕捉房价的主要影响因素。尽管个别样本存在较大误差，但总体趋势良好，说明模型具有较好的泛化性能。后续可通过计算均方误差（MSE）、决定系数（R²）等指标进一步量化评估模型表现，并考虑引入非线性项或更复杂的模型来提升精度。

6. 模型评估

6.1 常用评估指标说明

（1）评估指标说明

指标 计算公式 含义 理想值
均方误差（MSE） 1 n ∑ i = 1 n ( y i − y ^ i ) 2 \frac{1}{n}\sum_{i=1}^n(y_i-\hat{y}_i)^2 n1∑i=1n(yi−y^i)2 预测值与真实值之间平方误差的平均值，反映整体偏差大小 越小越好
均方根误差（RMSE） M S E \sqrt{MSE} MSE MSE 的平方根，单位与目标变量一致，便于直观理解误差水平 越小越好
决定系数（ R 2 R^2 R2） 1 − ∑ ( y i − y ^ i ) 2 ∑ ( y i − y ˉ ) 2 1-\frac{\sum(y_i-\hat{y}_i)^2}{\sum(y_i-\bar{y})^2} 1−∑(yi−yˉ)2∑(yi−y^i)2 表示模型解释目标变量变异的比例，取值范围为 [0,1] 越接近1越好

✅ 补充说明：

  • RMSE 是最常用的误差度量，因其与原始数据单位相同（千美元），易于解释；
  • R² 可用于比较不同模型的拟合优度，但需注意其受样本数量影响，不能单独作为最终评判标准。

（2）sklearn.metrics中的常用评估方法

除了score方法，还可使用sklearn.metrics模块中的函数计算其他指标，适用于LinearRegression等回归模型。

评估方法 功能说明 参数列表及说明 返回值
mean_squared_error(y_true, y_pred) 计算均方误差（MSE）：残差平方的均值，衡量误差的平方和 - y_true：真实目标变量（数组，[n_samples]或[n_samples, n_targets]） - y_pred：模型预测值（与y_true形状一致） - sample_weight（可选）：样本权重 - multioutput（可选）：多目标时的计算方式（默认'uniform_average'，平均所有目标的MSE） MSE值（浮点数，≥0，值越小越好）
mean_absolute_error(y_true, y_pred) 计算平均绝对误差（MAE）：绝对误差的均值，衡量误差的平均大小 参数同mean_squared_error MAE值（浮点数，≥0，值越小越好）
root_mean_squared_error(y_true, y_pred)（sklearn 1.2+） 计算均方根误差（RMSE）：MSE的平方根，单位与目标变量一致 参数同mean_squared_error RMSE值（浮点数，≥0，值越小越好）
r2_score(y_true, y_pred) 计算决定系数（R²），与LinearRegression.score结果一致 参数同mean_squared_error R²值（浮点数，越接近1越好）

6.2 评估代码实现与结果分析

在完成模型训练与预测后，必须通过科学的评估指标对模型性能进行全面衡量。此处采用回归任务中常用的三大评价指标------均方误差（MSE） 、均方根误差（RMSE） 和 决定系数（R²），分别计算训练集和测试集上的表现，并对比两者差异以判断是否存在过拟合现象。

实现代码如下所示：

python 复制代码 
# 计算评估指标
def evaluate(y_true, y_pred, dataset_name):
    mse = mean_squared_error(y_true, y_pred)
    rmse = np.sqrt(mse)
    r2 = r2_score(y_true, y_pred)
    print(f"\n=== {dataset_name} 评估指标 ===")
    print(f"均方误差（MSE）：{mse:.4f}")
    print(f"均方根误差（RMSE）：{rmse:.4f}（千美元）")
    print(f"决定系数（R²）：{r2:.4f}")
    return mse, rmse, r2

# 评估训练集
train_mse, train_rmse, train_r2 = evaluate(y_train, y_train_pred, "训练集")

# 评估测试集
test_mse, test_rmse, test_r2 = evaluate(y_test, y_test_pred, "测试集")

# 分析过拟合情况
if abs(train_r2 - test_r2) < 0.1:
    print("\n模型未出现明显过拟合（训练集与测试集R²差异较小）")
else:
    print("\n警告：模型可能存在过拟合（训练集与测试集R²差异较大）")

运行结果如下图所示，训练集 的 MSE 为 30.39、RMSE 约 5.51 千美元、R² 达到 0.65，表明模型在训练数据上能较好地拟合房价变化趋势；测试集 的 MSE 为 31.24，RMSE 略升至 5.59 千美元，R² 为 0.57，虽略有下降，但仍保持较高解释力；两者的 R² 差异仅为 0.0762 ，小于 0.1 的阈值，说明模型在测试集上的表现与训练集接近，未表现出明显的过拟合；RMSE 在两个集合间仅相差约 0.08 千美元，进一步验证了模型具有良好的泛化能力。

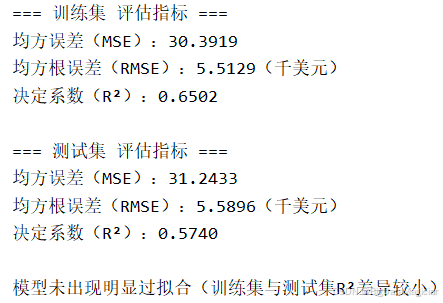
该线性回归模型在训练集和测试集上均取得了较为稳定的性能表现，具备较强的泛化能力。尽管 R² 值未达到理想水平（如 > 0.8），但在仅使用两个特征的情况下已取得不错的结果，体现了 RM 和 LSTAT 对房价的强大解释力。模型误差控制在合理范围内（约 ±5.5 千美元），适用于初步房价预测场景。

7. 结果可视化

为了更直观地理解模型的预测性能、误差分布以及特征对房价的影响程度，此处通过三幅关键图表进行可视化分析：真实值 vs 预测值散点图 、预测误差分布直方图 和 特征重要性条形图。这些图形不仅有助于评估模型表现，还能揭示潜在的问题与改进方向。

7.1 真实房价 vs 预测房价（散点图）

实现代码如下所示：

python 复制代码 
# 7.1 真实值 vs 预测值散点图
plt.figure(figsize=(10, 6))
# 绘制测试集真实值与预测值
plt.scatter(y_test, y_test_pred, alpha=0.7, color='blue', edgecolor='white', label='测试集')
# 绘制理想预测线（y=x）
plt.plot([y.min(), y.max()], [y.min(), y.max()], 'r--', label='理想预测线')
plt.title(f'真实房价 vs 预测房价 (R^2={test_r2:.4f})', fontsize=14)
plt.xlabel('真实房价（千美元）', fontsize=12)
plt.ylabel('预测房价（千美元）', fontsize=12)
plt.legend()
plt.grid(alpha=0.3)
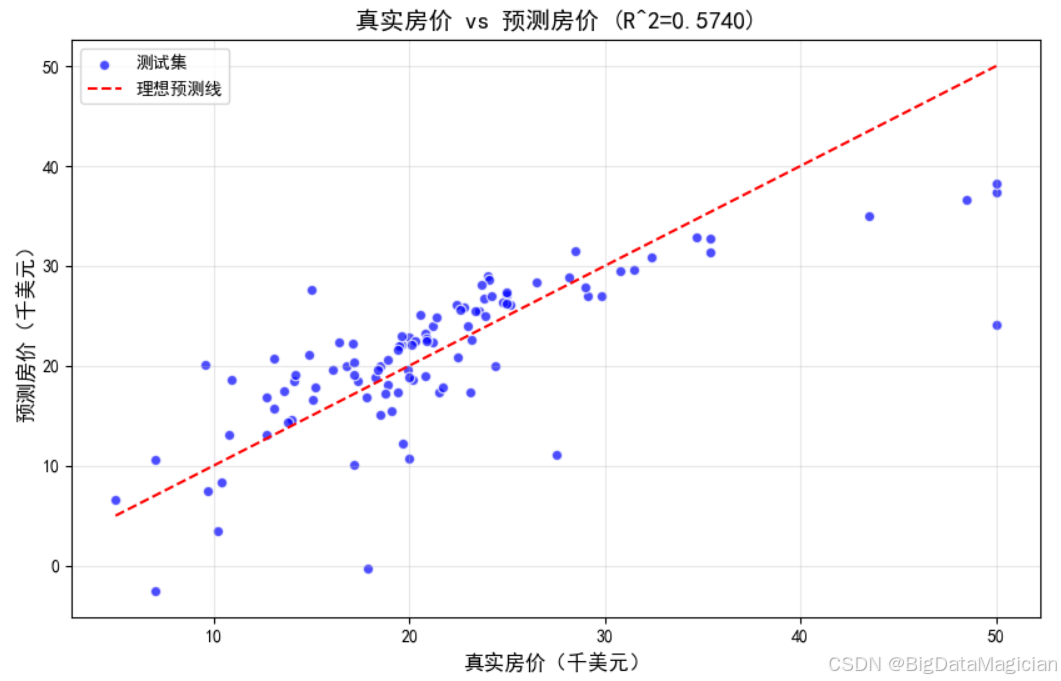
plt.show()

运行结果如下图所示，该图展示了测试集中每个样本的真实房价 与模型预测房价 之间的关系。理想情况下，所有点应落在红色虚线（即 y = x y = x y=x）附近，表示预测值完全等于真实值。从图中可以看出大部分数据点集中在理想预测线周围，说明模型整体具有较好的拟合能力；散点呈正相关趋势，表明模型能够捕捉房价的基本变化规律；少数点偏离较远，尤其在高房价区域存在明显偏差，可能由于极端值或非线性关系未被充分建模；图标题标注了决定系数 R 2 = 0.5740 R^2 = 0.5740 R2=0.5740，进一步量化了模型解释力；尽管存在一定误差，但整体趋势良好，验证了模型具备一定的泛化能力。

7.2 预测误差分布（直方图）

实现代码如下所示：

python 复制代码 
# 7.2 预测误差分布直方图
plt.figure(figsize=(10, 6))
errors = y_test - y_test_pred  # 计算误差（真实值-预测值）
plt.hist(errors, bins=20, alpha=0.7, color='orange', edgecolor='black')
plt.axvline(x=0, color='red', linestyle='--', label='零误差线')
plt.title(f'预测误差分布 (RMSE={test_rmse:.4f})', fontsize=14)
plt.xlabel('误差（千美元）', fontsize=12)
plt.ylabel('频数', fontsize=12)
plt.legend()
plt.grid(alpha=0.3)
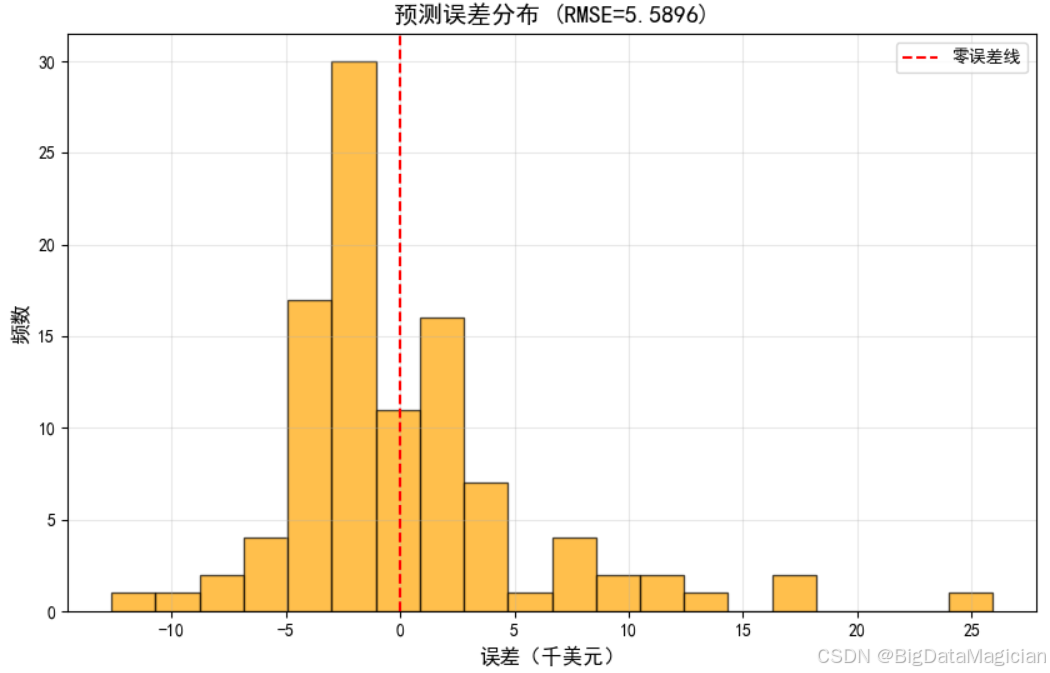
plt.show()

运行结果如下图所示，该图显示了测试集上每个样本的预测误差 （真实值 - 预测值）的分布情况。误差以"千美元"为单位，横轴代表误差大小，纵轴为频数。从图中可以看出，分布大致呈现近似对称的钟形曲线 ，中心位于零误差线（红色虚线）附近，说明大多数预测误差较小且无系统性偏移；误差主要集中在 [ − 10 , 10 ] [-10, 10] [−10,10] 千美元区间内，峰值出现在接近 0 的位置，表明模型多数情况下能较为准确地估计房价；少量极端误差超过 ±15 千美元，可能是异常样本或模型未能捕捉到的复杂因素所致；RMSE 值为 5.5896 千美元，对应于误差分布的标准差水平，进一步印证了模型误差可控。误差分布合理，无明显偏向性，说明模型没有系统性高估或低估，具备良好的稳定性。

7.3 特征重要性（基于回归系数绝对值）

实现代码如下所示：

python 复制代码 
# 7.3 特征重要性条形图（基于系数绝对值）
plt.figure(figsize=(12, 6))
# 计算特征重要性（系数绝对值）
feature_importance = np.abs(lr_model.coef_)
# 按重要性排序
sorted_idx = np.argsort(feature_importance)[::-1]

plt.bar([selected_features[i] for i in sorted_idx],
        [feature_importance[i] for i in sorted_idx],
        color=['green' if lr_model.coef_[i] > 0 else 'red' for i in sorted_idx])
plt.title('特征重要性（系数绝对值）', fontsize=14)
plt.xlabel('特征', fontsize=12)
plt.ylabel('系数绝对值（重要性）', fontsize=12)
plt.xticks(rotation=45, ha='right')
plt.grid(axis='y', alpha=0.3)
# 添加正负标记
for i in sorted_idx:
    plt.text(i, feature_importance[i] + 0.1,
             '+' if lr_model.coef_[i] > 0 else '-',
             ha='center', fontweight='bold')
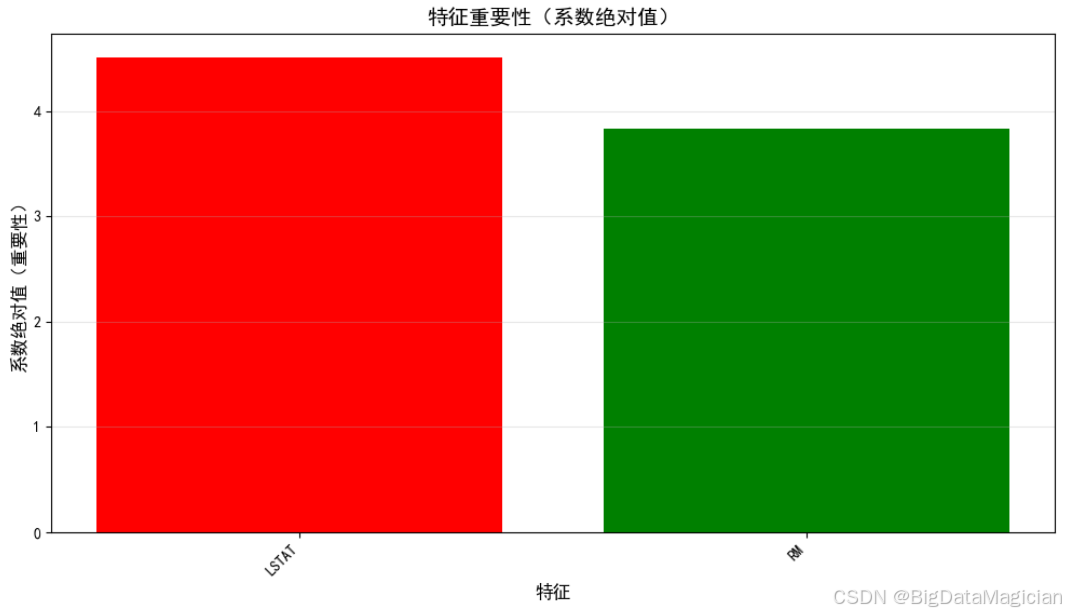
plt.show()

运行结果如下图所示，该条形图展示了两个特征在模型中的相对重要性 ，其依据是线性回归系数的绝对值。颜色编码用于区分影响方向：红色柱状图 ：LSTAT（低收入人群比例），系数为 -4.5122，绝对值最大，说明它是影响房价最强的变量，且呈负向作用------社区中低收入人口越多，房价越低；绿色柱状图 ：RM（平均房间数），系数为 +3.8361，虽略低于 LSTAT，但依然显著，表示房屋规模越大，价格越高。LSTAT 是模型中最关键的驱动因子，而 RM 也发挥了重要作用。两者共同构建了一个简洁而有意义的预测框架，符合现实经济逻辑。

7.4 结果解读

  1. 真实值vs预测值：点越接近红色虚线（y=x），预测效果越好；
  2. 误差分布：若误差近似正态分布且均值接近0，说明模型无系统性偏差；
  3. 特征重要性：系数绝对值越大，特征对房价影响越强（红色为负相关，绿色为正相关）。

8. 模型解释

模型的价值不仅体现在预测精度上，更在于其能否转化为可理解的业务洞察 或可操作的决策依据。线性回归因其结构透明、参数可解释性强，特别适合用于解释变量与目标之间的因果关系，从而支持房地产评估、政策制定、投资分析等实际应用场景。

8.1 回归系数的业务含义

在本模型中，最终保留了两个关键特征：RM（平均房间数）和 LSTAT（低收入人群比例）。它们的回归系数如下：

  • RM 系数 ≈ +3.8361

    表示在其他条件不变的情况下，房屋平均房间数每增加 1 个单位（标准化后） ，房价中位数预计上升约 3.84 千美元。这反映了房屋"规模"对价格的正向驱动作用------更大的居住空间通常意味着更高的市场价值。

  • LSTAT 系数 ≈ -4.5122

    表示社区中低收入人口比例每上升 1 个单位（标准化后） ，房价中位数预计下降约 4.51 千美元。这揭示了社会经济环境对房产价值的显著抑制效应------低收入集中区域往往伴随教育资源薄弱、治安较差等问题，导致房价承压。

注意：由于输入特征经过标准化处理，上述"1 个单位"指的是标准差的变化。若需解释原始尺度下的影响，可通过反标准化换算，或直接使用未缩放数据重新拟合模型以获得更具现实意义的系数。

8.2 特征重要性与决策支持

特征 系数符号 影响方向 业务解读
RM 正（+） 房价随房间数增加而上升 开发商可优先建设大户型住宅以提升溢价能力；购房者可将房间数作为核心估值指标
LSTAT 负（--） 房价随低收入比例上升而下降 政府可通过改善社区就业、教育水平来间接提升区域房产价值；投资者应警惕高 LSTAT 区域的资产贬值风险

8.3 模型的实际应用价值

  1. 自动化估价系统：可将该模型集成到在线房产平台，为用户提供快速、透明的房价估算；
  2. 政策效果模拟 ：政府可通过调整 LSTAT 相关的社会指标（如最低工资、保障房供给），预测其对区域房价的潜在影响；
  3. 投资组合优化：投资者可利用模型识别被低估或高估的区域，辅助资产配置决策；
  4. 特征监控预警 ：若未来某区域 LSTAT 显著上升，模型可发出房价下行预警，帮助业主或金融机构提前应对。

8.4 局限性与改进方向

尽管该模型具备良好的可解释性，但仍存在一定局限性。首先，仅基于两个特征（RM 和 LSTAT），忽略了地理位置、学区质量、交通便利性等可能显著影响房价的重要因素；其次，模型假设特征与房价之间存在线性关系，难以捕捉潜在的非线性效应，例如房间数过多可能导致单价边际递减；此外，由于输入特征经过标准化处理，回归系数反映的是标准差单位下的变化，难以直观转化为公众易于理解的实际房价变动，限制了其在面向非技术用户的场景中的直接应用。

五、完整代码

1. 完整代码

python 复制代码 
# 1. 导入库
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.datasets import fetch_openml
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split

# 设置matplotlib的中文字体为SimHei（黑体），以确保中文标签可以正常显示。
plt.rcParams['font.sans-serif'] = ['SimHei']
# 解决负号'-'显示为方块的问题，通过设置'axes.unicode_minus'为False来实现。
plt.rcParams['axes.unicode_minus'] = False

# 设置全局选项
pd.set_option('display.max_columns', None)  # 显示所有列
pd.set_option('display.width', None)  # 自动检测宽度
pd.set_option('display.max_colwidth', 50)  # 列内容最多显示50字符
pd.set_option('display.expand_frame_repr', False)  # 禁用多行表示（可选）

# 2. 加载并查看数据（波士顿房价数据集）
boston = fetch_openml(name="boston", version=1, as_frame=True, parser="pandas")

# 数据转换为DataFrame，便于查看
X = pd.DataFrame(boston.data, columns=boston.feature_names)
y = pd.Series(boston.target, name="MEDV")

##################################################
# 3. 数据探索与可视化（EDA）

# 3.1 数据基本信息查看
print("\n=== 数据集前5行 ===")
print(X.head())
print("\n=== 目标变量前5行 ===")
print(y.head())

print("\n=== 数据类型与缺失值 ===")
print(X.info())

print("\n=== 数值特征统计描述 ===")
print(X.describe())
print("\n=== 目标变量统计描述 ===")
print(y.describe())

# 3.2 目标变量分布分析
plt.figure(figsize=(10, 6))
# 绘制目标变量（房价）的直方图和核密度曲线
plt.hist(y, bins=30, density=True, alpha=0.7, color='skyblue', edgecolor='black')
y.plot(kind='kde', color='red', linewidth=2)  # 核密度估计曲线
plt.title('Distribution of Boston Housing Prices (MEDV)', fontsize=14)
plt.xlabel('Median Value ($1000s)', fontsize=12)
plt.ylabel('Density', fontsize=12)
plt.grid(alpha=0.3)
# plt.show()

# 3.3 特征与目标变量的相关性分析
# 计算所有特征与目标变量的相关系数
df_X = X.copy()
df_X['CHAS'] = df_X['CHAS'].astype(float)
df_X['RAD'] = df_X['RAD'].astype(float)
correlations = df_X.corrwith(y).sort_values(ascending=False)
print("\n=== 特征与目标变量（MEDV）的相关系数 ===")
print(correlations)

# 可视化相关性（条形图）
plt.figure(figsize=(12, 6))
correlations.plot(kind='bar', color=['green' if x > 0 else 'red' for x in correlations])
plt.title('Correlation Between Features and Housing Prices (MEDV)', fontsize=14)
plt.axhline(y=0, color='black', linestyle='--', alpha=0.3)  # 添加水平线（y=0）
plt.xlabel('Features', fontsize=12)
plt.ylabel('Correlation Coefficient', fontsize=12)
plt.grid(axis='y', alpha=0.3)
plt.xticks(rotation=45, ha='right')  # 旋转x轴标签，避免重叠
# plt.show()

# 3.4 强相关特征与目标变量的散点图
# 选择与目标变量相关性最强的2个正相关和2个负相关特征
top_positive = correlations.index[:2]  # 前2个正相关特征
top_negative = correlations.index[-2:]  # 最后2个负相关特征
selected_features = list(top_positive) + list(top_negative)

plt.figure(figsize=(15, 10))
for i, feature in enumerate(selected_features, 1):
    plt.subplot(2, 2, i)
    plt.scatter(X[feature], y, alpha=0.6, color='purple', edgecolor='white', s=30)
    # 添加趋势线（线性拟合）
    z = np.polyfit(X[feature], y, 1)
    p = np.poly1d(z)
    plt.plot(X[feature], p(X[feature]), "r--")
    plt.title(f'{feature} vs MEDV (Corr: {correlations[feature]:.2f})', fontsize=12)
    plt.xlabel(feature, fontsize=10)
    plt.ylabel('MEDV ($1000s)', fontsize=10)
    plt.grid(alpha=0.3)

plt.tight_layout()  # 调整子图间距
# plt.show()

# 3.5 特征间的相关性热力图
plt.figure(figsize=(14, 10))
# 计算所有特征间的相关系数矩阵
corr_matrix = X.corr()
# 绘制热力图
import seaborn as sns

sns.heatmap(corr_matrix, annot=True, fmt=".2f", cmap='coolwarm',
            square=True, linewidths=0.5, cbar_kws={"shrink": .8})
plt.title('Correlation Matrix of Features', fontsize=14)
plt.xticks(rotation=45, ha='right')
plt.yticks(rotation=0)
# plt.show()
##################################################
# 方法1：基于相关系数手动筛选（选择绝对值>0.5的特征）
corr_threshold = 0.5
selected_features = correlations[abs(correlations) > corr_threshold].index.tolist()
print(f"\n基于相关系数筛选的特征（|corr| > {corr_threshold}）：{selected_features}")

# 方法2：计算VIF剔除多重共线性特征（可选）
from statsmodels.stats.outliers_influence import variance_inflation_factor


def calculate_vif(X):
    vif_data = pd.DataFrame()
    vif_data["特征"] = X.columns
    vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
    return vif_data.sort_values("VIF", ascending=False)


# 初始VIF计算
vif_df = calculate_vif(X[selected_features])
print("\n初始VIF值：")
print(vif_df)

# 剔除VIF>10的特征（通常认为VIF>10存在强共线性）
while vif_df["VIF"].max() > 10:
    # 删除VIF最大的特征
    drop_feature = vif_df.iloc[0]["特征"]
    selected_features.remove(drop_feature)
    vif_df = calculate_vif(X[selected_features])
    print(f"\n剔除特征 {drop_feature} 后VIF值：")
    print(vif_df)

# 更新特征矩阵
X_selected = X[selected_features]
print(f"\n最终筛选后的特征：{selected_features}")
##################################################
from sklearn.preprocessing import StandardScaler

# 初始化标准化器
scaler = StandardScaler()

# 对筛选后的特征进行标准化
X_scaled = scaler.fit_transform(X_selected)

# 转换为DataFrame便于查看
X_scaled_df = pd.DataFrame(X_scaled, columns=selected_features)
print("\n标准化后的特征前5行：")
print(X_scaled_df.head())
print("\n标准化后特征的均值和标准差：")
print(pd.DataFrame({
    "均值": X_scaled_df.mean().round(4),
    "标准差": X_scaled_df.std().round(4)
}))
##################################################
# 划分训练集和测试集（测试集占20%）
X_train, X_test, y_train, y_test = train_test_split(
    X_scaled,  # 标准化后的特征
    y.values,  # 目标变量（转为数组）
    test_size=0.2,  # 测试集比例
    random_state=42  # 随机种子，保证结果可复现
)

# 查看划分后的数据形状
print(f"\n训练集特征形状：{X_train.shape}，测试集特征形状：{X_test.shape}")
print(f"训练集目标形状：{y_train.shape}，测试集目标形状：{y_test.shape}")
##################################################
# 初始化线性回归模型
lr_model = LinearRegression(fit_intercept=True)

# 使用训练集训练模型
lr_model.fit(X_train, y_train)

# 查看模型参数
print("=== 线性回归模型参数 ===")
print(f"截距项（w0）：{lr_model.intercept_:.4f}")
print("特征系数（w1...wn）：")
for feature, coef in zip(selected_features, lr_model.coef_):
    print(f"  {feature}: {coef:.4f}")
##################################################
# 对训练集和测试集进行预测
y_train_pred = lr_model.predict(X_train)  # 训练集预测值
y_test_pred = lr_model.predict(X_test)  # 测试集预测值

# 查看部分预测结果
print("\n=== 预测结果示例（前5条） ===")
comparison = pd.DataFrame({
    "真实值": y_test,
    "预测值": y_test_pred,
    "误差": (y_test_pred - y_test).round(2)
})
comparison.to_csv("线性回归预测结果.csv", index=False)
print(comparison)


##################################################
# 计算评估指标
def evaluate(y_true, y_pred, dataset_name):
    mse = mean_squared_error(y_true, y_pred)
    rmse = np.sqrt(mse)
    r2 = r2_score(y_true, y_pred)
    print(f"\n=== {dataset_name} 评估指标 ===")
    print(f"均方误差（MSE）：{mse:.4f}")
    print(f"均方根误差（RMSE）：{rmse:.4f}（千美元）")
    print(f"决定系数（R²）：{r2:.4f}")
    return mse, rmse, r2


# 评估训练集
train_mse, train_rmse, train_r2 = evaluate(y_train, y_train_pred, "训练集")

# 评估测试集
test_mse, test_rmse, test_r2 = evaluate(y_test, y_test_pred, "测试集")

# 分析过拟合情况
if abs(train_r2 - test_r2) < 0.1:
    print("\n模型未出现明显过拟合（训练集与测试集R²差异较小）")
else:
    print("\n警告：模型可能存在过拟合（训练集与测试集R²差异较大）")
##################################################
# 7.1 真实值 vs 预测值散点图
plt.figure(figsize=(10, 6))
# 绘制测试集真实值与预测值
plt.scatter(y_test, y_test_pred, alpha=0.7, color='blue', edgecolor='white', label='测试集')
# 绘制理想预测线（y=x）
plt.plot([y.min(), y.max()], [y.min(), y.max()], 'r--', label='理想预测线')
plt.title(f'真实房价 vs 预测房价 (R^2={test_r2:.4f})', fontsize=14)
plt.xlabel('真实房价（千美元）', fontsize=12)
plt.ylabel('预测房价（千美元）', fontsize=12)
plt.legend()
plt.grid(alpha=0.3)
plt.show()

# 7.2 预测误差分布直方图
plt.figure(figsize=(10, 6))
errors = y_test - y_test_pred  # 计算误差（真实值-预测值）
plt.hist(errors, bins=20, alpha=0.7, color='orange', edgecolor='black')
plt.axvline(x=0, color='red', linestyle='--', label='零误差线')
plt.title(f'预测误差分布 (RMSE={test_rmse:.4f})', fontsize=14)
plt.xlabel('误差（千美元）', fontsize=12)
plt.ylabel('频数', fontsize=12)
plt.legend()
plt.grid(alpha=0.3)
plt.show()

# 7.3 特征重要性条形图（基于系数绝对值）
plt.figure(figsize=(12, 6))
# 计算特征重要性（系数绝对值）
feature_importance = np.abs(lr_model.coef_)
# 按重要性排序
sorted_idx = np.argsort(feature_importance)[::-1]

plt.bar([selected_features[i] for i in sorted_idx],
        [feature_importance[i] for i in sorted_idx],
        color=['green' if lr_model.coef_[i] > 0 else 'red' for i in sorted_idx])
plt.title('特征重要性（系数绝对值）', fontsize=14)
plt.xlabel('特征', fontsize=12)
plt.ylabel('系数绝对值（重要性）', fontsize=12)
plt.xticks(rotation=45, ha='right')
plt.grid(axis='y', alpha=0.3)

plt.show()

2. 优化后完整代码

python 复制代码 
# 波士顿房价线性回归分析
# 功能：通过线性回归模型分析影响波士顿房价的关键因素并进行预测

# ----------------------------
# 1. 导入必要的库
# ----------------------------
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
from sklearn.datasets import fetch_openml
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from statsmodels.stats.outliers_influence import variance_inflation_factor

# 设置matplotlib的中文字体为SimHei（黑体），以确保中文标签可以正常显示。
plt.rcParams['font.sans-serif'] = ['SimHei']
# 解决负号'-'显示为方块的问题，通过设置'axes.unicode_minus'为False来实现。
plt.rcParams['axes.unicode_minus'] = False

# 设置pandas显示参数
pd.set_option('display.max_columns', None)  # 显示所有列
pd.set_option('display.width', None)  # 自动检测宽度
pd.set_option('display.max_colwidth', 50)  # 列内容最多显示50字符
pd.set_option('display.expand_frame_repr', False)  # 禁用多行表示（可选）


# ----------------------------
# 2. 数据加载与预处理
# ----------------------------
def load_and_prepare_data():
    """加载波士顿房价数据并进行初步处理"""
    print("正在加载波士顿房价数据集...")
    # 加载数据集
    boston = fetch_openml(name="boston", version=1, as_frame=True, parser="pandas")

    # 提取特征和目标变量
    X = pd.DataFrame(boston.data, columns=boston.feature_names)
    y = pd.Series(boston.target, name="MEDV")  # MEDV: 以千美元为单位的房价中位数

    # 转换分类特征为数值类型
    X['CHAS'] = X['CHAS'].astype(float)  # 查尔斯河虚拟变量
    X['RAD'] = X['RAD'].astype(float)  # 径向公路可达性指数

    print(f"数据集加载完成 - 特征数量: {X.shape[1]}, 样本数量: {X.shape[0]}")
    return X, y


# ----------------------------
# 3. 数据探索与可视化 (EDA)
# ----------------------------
def perform_eda(X, y):
    """执行探索性数据分析"""
    print("\n" + "=" * 50)
    print("开始探索性数据分析 (EDA)")
    print("=" * 50)

    # 3.1 数据基本信息查看
    print("\n--- 数据集前5行 ---")
    print(X.head())
    print("\n--- 目标变量前5行 ---")
    print(y.head())

    print("\n--- 数据类型与缺失值 ---")
    print(X.info())

    print("\n--- 数值特征统计描述 ---")
    print(X.describe().round(2))
    print("\n--- 目标变量统计描述 ---")
    print(y.describe().round(2))

    # 3.2 目标变量分布分析
    plt.figure(figsize=(10, 6))
    plt.hist(y, bins=30, density=True, alpha=0.7, color='skyblue', edgecolor='black')
    y.plot(kind='kde', color='red', linewidth=2)
    plt.title('波士顿房价分布 (MEDV)', fontsize=14)
    plt.xlabel('房价中位数（千美元）', fontsize=12)
    plt.ylabel('密度', fontsize=12)
    plt.grid(alpha=0.3)
    plt.tight_layout()
    plt.savefig('房价分布.png', dpi=300)
    # plt.show()

    # 3.3 特征与目标变量的相关性分析
    correlations = X.corrwith(y).sort_values(ascending=False)
    print("\n--- 特征与房价的相关系数 ---")
    print(correlations.round(3))

    # 可视化相关性
    plt.figure(figsize=(12, 6))
    correlations.plot(kind='bar', color=['green' if x > 0 else 'red' for x in correlations])
    plt.title('特征与房价的相关性', fontsize=14)
    plt.axhline(y=0, color='black', linestyle='--', alpha=0.3)
    plt.xlabel('特征', fontsize=12)
    plt.ylabel('相关系数', fontsize=12)
    plt.grid(axis='y', alpha=0.3)
    plt.xticks(rotation=45, ha='right')
    plt.tight_layout()
    plt.savefig('特征相关性.png', dpi=300)
    # plt.show()

    # 3.4 强相关特征与目标变量的散点图
    top_positive = correlations.index[:2]  # 前2个正相关特征
    top_negative = correlations.index[-2:]  # 最后2个负相关特征
    selected_features = list(top_positive) + list(top_negative)

    plt.figure(figsize=(15, 10))
    for i, feature in enumerate(selected_features, 1):
        plt.subplot(2, 2, i)
        plt.scatter(X[feature], y, alpha=0.6, color='purple', edgecolor='white', s=30)
        # 添加趋势线
        z = np.polyfit(X[feature], y, 1)
        p = np.poly1d(z)
        plt.plot(X[feature], p(X[feature]), "r--")
        plt.title(f'{feature} 与房价的关系 (相关系数: {correlations[feature]:.2f})', fontsize=12)
        plt.xlabel(feature, fontsize=10)
        plt.ylabel('房价（千美元）', fontsize=10)
        plt.grid(alpha=0.3)

    plt.tight_layout()
    plt.savefig('强相关特征散点图.png', dpi=300)
    # plt.show()

    # 3.5 特征间的相关性热力图
    plt.figure(figsize=(14, 10))
    corr_matrix = X.corr()
    sns.heatmap(corr_matrix, annot=True, fmt=".2f", cmap='coolwarm',
                square=True, linewidths=0.5, cbar_kws={"shrink": .8})
    plt.title('特征间相关性热力图', fontsize=14)
    plt.xticks(rotation=45, ha='right')
    plt.yticks(rotation=0)
    plt.tight_layout()
    plt.savefig('特征相关性热力图.png', dpi=300)
    # plt.show()

    return correlations


# ----------------------------
# 4. 特征选择
# ----------------------------
def select_features(X, correlations):
    """基于相关系数和VIF值选择最佳特征集"""
    print("\n" + "=" * 50)
    print("开始特征选择")
    print("=" * 50)

    # 方法1：基于相关系数筛选（选择绝对值>0.5的特征）
    corr_threshold = 0.5
    selected_features = correlations[abs(correlations) > corr_threshold].index.tolist()
    print(f"基于相关系数筛选的特征（|corr| > {corr_threshold}）：{selected_features}")

    # 方法2：计算VIF剔除多重共线性特征
    def calculate_vif(X_df):
        """计算特征的方差膨胀因子"""
        vif_data = pd.DataFrame()
        vif_data["特征"] = X_df.columns
        vif_data["VIF"] = [variance_inflation_factor(X_df.values, i)
                           for i in range(X_df.shape[1])]
        return vif_data.sort_values("VIF", ascending=False)

    # 初始VIF计算
    vif_df = calculate_vif(X[selected_features])
    print("\n初始VIF值：")
    print(vif_df.round(2))

    # 剔除VIF>10的特征（通常认为VIF>10存在强共线性）
    while vif_df["VIF"].max() > 10:
        # 删除VIF最大的特征
        drop_feature = vif_df.iloc[0]["特征"]
        selected_features.remove(drop_feature)
        vif_df = calculate_vif(X[selected_features])
        print(f"\n剔除特征 {drop_feature} 后VIF值：")
        print(vif_df.round(2))

    # 更新特征矩阵
    X_selected = X[selected_features]
    print(f"\n最终筛选后的特征：{selected_features}")

    return X_selected, selected_features


# ----------------------------
# 5. 特征标准化与数据集划分
# ----------------------------
def preprocess_and_split(X_selected, y):
    """标准化特征并划分训练集和测试集"""
    print("\n" + "=" * 50)
    print("开始特征标准化与数据集划分")
    print("=" * 50)

    # 特征标准化
    scaler = StandardScaler()
    X_scaled = scaler.fit_transform(X_selected)

    # 转换为DataFrame便于查看
    X_scaled_df = pd.DataFrame(X_scaled, columns=X_selected.columns)
    print("\n标准化后的特征前5行：")
    print(X_scaled_df.head().round(4))
    print("\n标准化后特征的均值和标准差：")
    print(pd.DataFrame({
        "均值": X_scaled_df.mean().round(4),
        "标准差": X_scaled_df.std().round(4)
    }))

    # 划分训练集和测试集（测试集占20%）
    X_train, X_test, y_train, y_test = train_test_split(
        X_scaled,
        y.values,
        test_size=0.2,
        random_state=42  # 固定随机种子，保证结果可复现
    )

    # 查看划分后的数据形状
    print(f"\n训练集特征形状：{X_train.shape}，测试集特征形状：{X_test.shape}")
    print(f"训练集目标形状：{y_train.shape}，测试集目标形状：{y_test.shape}")

    return X_train, X_test, y_train, y_test, scaler


# ----------------------------
# 6. 模型训练与预测
# ----------------------------
def train_and_predict(X_train, X_test, y_train, selected_features):
    """训练线性回归模型并进行预测"""
    print("\n" + "=" * 50)
    print("开始模型训练与预测")
    print("=" * 50)

    # 初始化并训练线性回归模型
    lr_model = LinearRegression(fit_intercept=True)
    lr_model.fit(X_train, y_train)

    # 查看模型参数
    print("\n--- 线性回归模型参数 ---")
    print(f"截距项（w0）：{lr_model.intercept_:.4f}")
    print("特征系数（w1...wn）：")
    for feature, coef in zip(selected_features, lr_model.coef_):
        print(f"  {feature}: {coef:.4f} ({'正相关' if coef > 0 else '负相关'})")

    # 进行预测
    y_train_pred = lr_model.predict(X_train)
    y_test_pred = lr_model.predict(X_test)

    # 保存并查看部分预测结果
    print("\n--- 预测结果示例（前5条） ---")
    comparison = pd.DataFrame({
        "真实值": y_test[:5].round(2),
        "预测值": y_test_pred[:5].round(2),
        "误差": (y_test_pred[:5] - y_test[:5]).round(2)
    })
    comparison.to_csv("线性回归预测结果.csv", index=False)
    print(comparison)

    return lr_model, y_train_pred, y_test_pred


# ----------------------------
# 7. 模型评估
# ----------------------------
def evaluate_model(y_train, y_train_pred, y_test, y_test_pred):
    """评估模型性能并可视化结果"""
    print("\n" + "=" * 50)
    print("开始模型评估")
    print("=" * 50)

    # 评估指标计算函数
    def evaluate(y_true, y_pred, dataset_name):
        mse = mean_squared_error(y_true, y_pred)
        rmse = np.sqrt(mse)
        r2 = r2_score(y_true, y_pred)
        print(f"\n--- {dataset_name} 评估指标 ---")
        print(f"均方误差（MSE）：{mse:.4f}")
        print(f"均方根误差（RMSE）：{rmse:.4f}（千美元）")
        print(f"决定系数（R²）：{r2:.4f}")
        return mse, rmse, r2

    # 评估训练集和测试集
    train_mse, train_rmse, train_r2 = evaluate(y_train, y_train_pred, "训练集")
    test_mse, test_rmse, test_r2 = evaluate(y_test, y_test_pred, "测试集")

    # 分析过拟合情况
    if abs(train_r2 - test_r2) < 0.1:
        print("\n模型未出现明显过拟合（训练集与测试集R²差异较小）")
    else:
        print("\n警告：模型可能存在过拟合（训练集与测试集R²差异较大）")

    return train_r2, test_r2, test_rmse


# ----------------------------
# 8. 结果可视化
# ----------------------------
def visualize_results(y_test, y_test_pred, test_r2, test_rmse, lr_model, selected_features):
    """可视化模型结果"""
    print("\n" + "=" * 50)
    print("开始结果可视化")
    print("=" * 50)

    # 8.1 真实值 vs 预测值散点图
    plt.figure(figsize=(10, 6))
    plt.scatter(y_test, y_test_pred, alpha=0.7, color='blue', edgecolor='white', label='测试集')
    plt.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'r--', label='理想预测线')
    plt.title(f'真实房价 vs 预测房价 (R^2={test_r2:.4f})', fontsize=14)
    plt.xlabel('真实房价（千美元）', fontsize=12)
    plt.ylabel('预测房价（千美元）', fontsize=12)
    plt.legend()
    plt.grid(alpha=0.3)
    plt.tight_layout()
    plt.savefig('真实值vs预测值.png', dpi=300)
    # plt.show()

    # 8.2 预测误差分布直方图
    plt.figure(figsize=(10, 6))
    errors = y_test - y_test_pred  # 计算误差（真实值-预测值）
    plt.hist(errors, bins=20, alpha=0.7, color='orange', edgecolor='black')
    plt.axvline(x=0, color='red', linestyle='--', label='零误差线')
    plt.title(f'预测误差分布 (RMSE={test_rmse:.4f})', fontsize=14)
    plt.xlabel('误差（千美元）', fontsize=12)
    plt.ylabel('频数', fontsize=12)
    plt.legend()
    plt.grid(alpha=0.3)
    plt.tight_layout()
    plt.savefig('预测误差分布.png', dpi=300)
    # plt.show()

    # 8.3 特征重要性条形图（基于系数绝对值）
    plt.figure(figsize=(12, 6))
    feature_importance = np.abs(lr_model.coef_)
    sorted_idx = np.argsort(feature_importance)[::-1]

    plt.bar([selected_features[i] for i in sorted_idx],
            [feature_importance[i] for i in sorted_idx],
            color=['green' if lr_model.coef_[i] > 0 else 'red' for i in sorted_idx])
    plt.title('特征重要性（系数绝对值）', fontsize=14)
    plt.xlabel('特征', fontsize=12)
    plt.ylabel('系数绝对值（重要性）', fontsize=12)
    plt.xticks(rotation=45, ha='right')
    plt.grid(axis='y', alpha=0.3)
    plt.tight_layout()
    plt.savefig('特征重要性.png', dpi=300)
    # plt.show()


# 程序入口
if __name__ == "__main__":
    """主函数：执行波士顿房价分析的完整流程"""
    print("=" * 70)
    print("          波士顿房价线性回归分析          ")
    print("=" * 70)

    # 执行完整分析流程
    X, y = load_and_prepare_data()
    correlations = perform_eda(X, y)
    X_selected, selected_features = select_features(X, correlations)
    X_train, X_test, y_train, y_test, scaler = preprocess_and_split(X_selected, y)
    lr_model, y_train_pred, y_test_pred = train_and_predict(X_train, X_test, y_train, selected_features)
    train_r2, test_r2, test_rmse = evaluate_model(y_train, y_train_pred, y_test, y_test_pred)
    visualize_results(y_test, y_test_pred, test_r2, test_rmse, lr_model, selected_features)

    print("\n" + "=" * 70)
    print("          分析完成！所有结果已保存          ")
    print("=" * 70)
相关推荐
Dev7z7 小时前
基于ResNet50和PyTorch的猫狗图像分类系统设计与实现
人工智能·pytorch·分类
蒋星熠10 小时前
多模态技术深度探索：融合视觉与语言的AI新范式
人工智能·python·深度学习·机器学习·分类·数据挖掘·多分类
husterlichf1 天前
回归问题——相关误差指标数学概念详解以及sklearn.metrics相关方法
人工智能·机器学习·线性回归
渔舟渡简1 天前
机器学习-回归分析之一元线性回归
机器学习·线性回归
算法与编程之美1 天前
探索不同的优化器对分类精度的影响和卷积层的输入输出的shape的计算公式
人工智能·深度学习·机器学习·分类·数据挖掘
云茧1 天前
机器学习中的Hello World：线性回归（一）
人工智能·机器学习·线性回归
大数据魔法师2 天前
分类与回归算法（一）- 模型评价指标
分类·数据挖掘·回归
王哈哈^_^2 天前
【数据集】【YOLO】目标检测游泳数据集 4481 张，溺水数据集，YOLO河道、海滩游泳识别算法实战训练教程。
人工智能·算法·yolo·目标检测·计算机视觉·分类·视觉检测
极客数模2 天前
2025年（第六届）“大湾区杯”粤港澳金融数学建模竞赛准备！严格遵循要求，拿下大奖！
大数据·python·数学建模·金融·分类·图论·boosting
热门推荐
01GitHub 镜像站点02综合整理：pdf预览显示：你尝试预览的文件可能对你的计算机有害。如果你信任此文件以及其来源，请打开此文件以看其内容，如何解决以正常预览文件03UV安装并设置国内源04npm使用国内淘宝镜像的方法05Linux下V2Ray安装配置指南06BongoCat - 跨平台键盘猫动画工具07《大数据技术原理与应用》实验报告三 熟悉HBase常用操作08NVIDIA显卡驱动、CUDA、cuDNN 和 TensorRT 版本匹配指南09安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）10GitLab 零基础入门指南：从安装到项目管理全流程