文章目录
前言:
论文标题"Jointly Learning to Align and Translate"点明了其核心贡献:模型在一个统一的框架内,同时学习翻译任务和源语言与目标语言之间的词语对齐关系 。这种对齐是通过注意力权重 αij 隐式学习得到的,它量化了在生成目标词 yi 时,对源词 xj 的关注程度。
(1)编码器工作机制
【1】普通RNN的局限
一个标准的循环神经网络RNN会从第一个符号 x_1 到最后一个符号 x_{T_x} 顺序地 读取输入序列
h t = f ( x t , h t − 1 ) \quad h_t = f(x_t, h_{t-1}) ht=f(xt,ht−1)
这种单向结构导致每个隐藏状态 h_t 主要包含了到当前时刻为止的历史信息 ,无法获取未来时刻的上下文。
【2】双向RNN:获取完整上下文
为了克服这一局限,本文采用了双向RNN ,其核心思想是为每个词生成一个同时囊括了前文 和后文 信息的上下文表示。
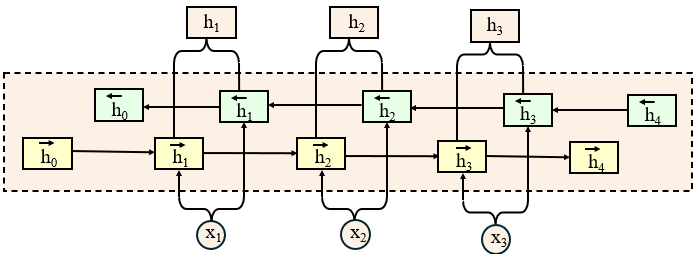
如图所示,双向RNN由两个独立的RNN组成:
- 前向RNN ( RNN → \overrightarrow{\text{RNN}} RNN ):从
x_1到x_{T_x}顺序读取输入,生成隐藏状态 h j → \overrightarrow{h_j} hj ,它总结了第j个词之前的所有上文信息。 - 反向RNN ( RNN ← \overleftarrow{\text{RNN}} RNN ):从
x_{T_x}到x_1逆序读取输入,生成隐藏状态 h j ← \overleftarrow{h_j} hj ,它总结了第j个词之后的所有下文信息。
最终,我们将每个位置 j 的前向与反向隐藏状态进行拼接 ,得到该词的最终注解向量 h_j:
(2)解码器工作机制
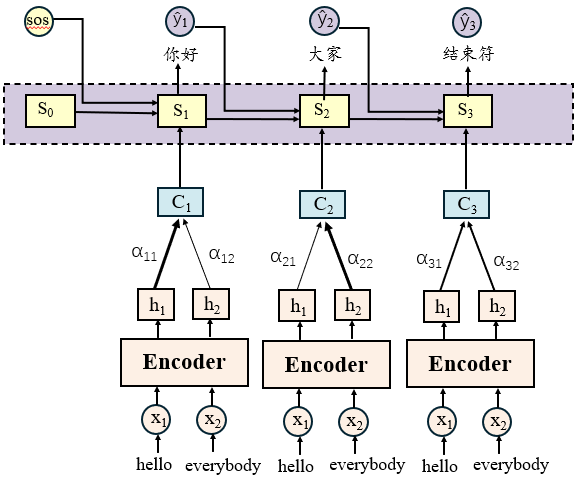
下面我将按照训练阶段的逻辑顺序来讲解解码器的完整工作流程,这样能更好地理解各个组件如何协同工作。整个流程如图所示:
【1】输入准备
训练阶段采用Teacher Forcing策略:
- 编码器输入:完整的源语言序列
x - 解码器输入:真实标签的前缀
y_1, ..., y_{i-1} - 目标输出:下一个真实标签
y_i
【2】能量分数计算
在生成目标词 y_i 时,计算解码器前一状态 s_{i−1} 与每个编码器标注 h_j 的匹配程度:
e i j = a ( s i − 1 , h j ) e_{ij} = a(s_{i-1}, h_j) eij=a(si−1,hj)
其中a是一个前馈神经网络,附录A.1.2补充了具体形式:
e i j = a ( s i − 1 , h j ) = v a T ⋅ t a n h ( W a ⋅ s i − 1 + U a ⋅ h j ) e_{ij} = a(s_{i-1}, h_j) = v_a^T · tanh(W_a · s_{i-1} + U_a · h_j) eij=a(si−1,hj)=vaT⋅tanh(Wa⋅si−1+Ua⋅hj)
其中:
-
W_a ∈ R^(d×d_s):解码器状态的权重矩阵(d_s为状态维度,d为对齐模型的隐藏层维度) -
U_a ∈ R^(d×d_h):编码器标注的权重矩阵(d_h为标注维度) -
v_a ∈ R^d:输出权重向量,将d维隐藏层映射到标量分数(一个值)理解:a作为一个对齐模型,里面有许多我们需要学习的参数,一旦学习到这个参数,我们就可以直接进行预测
【3】注意力权重计算
通过Softmax函数将能量分数转换为概率分布的注意力权重:
α i j = exp ( e i j ) ∑ k = 1 T x exp ( e i k ) \alpha_{ij} = \frac{\exp(e_{ij})}{\sum_{k=1}^{T_x} \exp(e_{ik})} αij=∑k=1Txexp(eik)exp(eij)
与能量分数意义相同,即在生成当前目标词 y_i时,编码器标注 h_j 相对于解码器状态 s_{i-1} 的重要性程度。
【4】注意力上下文向量计算
在获得注意力权重后,我们通过加权求和的方式生成上下文向量:
c i = α i 1 ⋅ h 1 + α i 2 ⋅ h 2 + . . . + α i T x ⋅ h T x ci = α_{i1}·h₁ + α_{i2}·h₂ + ... + α_{i{T_x}}·h_{T_x} ci=αi1⋅h1+αi2⋅h2+...+αiTx⋅hTx
对于当前输出 y_i ,编码器中重要的信息会被放大 ,不重要的被抑制
【5】解码器状态更新
整合三方面信息更新解码器状态:
s i = f ( s i − 1 , y i − 1 , c i ) s_i = f(s_{i-1}, y_{i-1}, c_i) si=f(si−1,yi−1,ci)
其中:
-
s_{i-1}:历史状态信息 -
y_{i-1}:前一个真实标签 -
c_i:注意力上下文理解:函数 f 通常实现为GRU或LSTM等RNN单元,同上面的a模型,f里面有许多我们需要学习的参数,一旦学习到这个参数,我们就可以直接进行预测
【6】目标词概率生成
基于所有可用信息生成目标词的概率分布:
p ( y i ∣ y 1 , ... , y i − 1 , x ) = g ( y i − 1 , s i , c i ) p(y_i | y_1, \ldots, y_{i-1}, \mathbf{x}) = g(y_{i-1}, s_i, c_i) p(yi∣y1,...,yi−1,x)=g(yi−1,si,ci)
函数 (g) 的典型实现流程:
python
输入 = [y_{i-1}的嵌入向量, s_i, c_i] # 向量拼接
隐藏层 = tanh(W_h · 输入 + b_h) # 非线性变换
logits = W_o · 隐藏层 + b_o # 输出层,得到词汇分数
p(y_i) = softmax(logits) # 转换为概率分布【7】损失计算与反向传播
- 计算交叉熵损失:
loss = -log(p(y_i)) - 累加所有时间步的损失
- 一次性反向传播更新所有参数
训练过程示例:
python
第1步:解码器输入<sos> → 预测"你好" (与真实标签"你好"计算交叉熵损失)
第2步:解码器输入真实标签"你好" → 预测"大家" (与真实标签"大家"计算交叉熵损失)
第3步:解码器输入真实标签"大家" → 预测<eos> (与真实标签<eos>计算交叉熵损失)
第4步:累加所有步骤损失 → 反向传播更新参数【8】从训练到预测
预测阶段采用自回归生成方式,与训练阶段的主要区别:
| 方面 | 训练阶段 | 预测阶段 |
|---|---|---|
| 输入来源 | 真实标签 y_{i-1} |
模型预测 ŷ_{i-1} |
| 目标 | 学习正确映射 | 生成完整序列 |
| 错误处理 | 避免错误累积 | 可能错误传播 |
预测过程示例:
python
第1步:解码器输入<sos> → 预测ŷ₁ = "你好"
第2步:解码器输入上一步的预测结果ŷ₁ → 预测ŷ₂ = "大家"
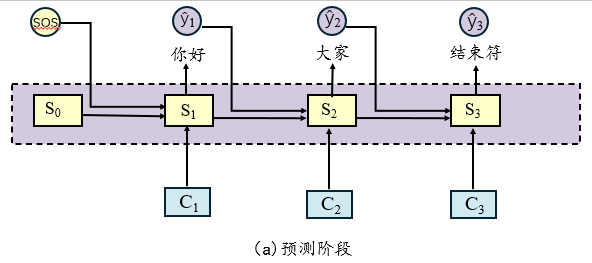
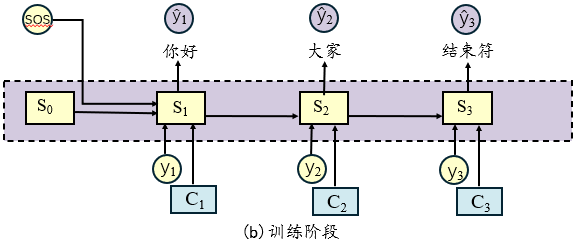
第3步:解码器输入上一步的预测结果ŷ₂ → 预测ŷ₃ = <eos> (停止生成)这两者的区别,如图所示:
、