LSTM门控结构：乘法设计的必然性分析

LSTM作者Hochreiter和Schmidhuber选择乘法门控 而非加法或卷积，是基于理论设计与实验验证的系统性决策，还是"灵光一现"？

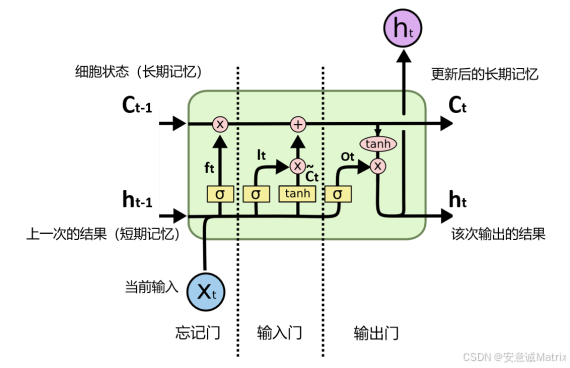
以下从三个维度解析这一选择：

一、理论设计：乘法是"门控"的数学本质

1. 门控的物理意义与乘法的完美契合

• sigmoid输出(0-1)的物理含义：0表示"完全阻断"，1表示"完全通过"，0.5表示"半开"

• 乘法操作的天然匹配 ：

  门控值 × 信息流 = 筛选后的信息流
  0 × 任何值 = 0 (信息完全丢弃)
  1 × 任何值 = 原值 (信息完全保留)
  0.5 × 信息流 = 保留50%信息 (精细调节)

• 加法的不匹配：加法是信息叠加而非筛选，无法实现"关闭"功能(0+信息流=信息流，无法阻断)

• 卷积的冗余 ：卷积用于空间特征提取，而LSTM处理的是时序信息流动，乘法更直接高效

2. 梯度控制：LSTM的核心使命

• 乘法门控实现梯度的"选择性传递"：门控值直接乘在梯度上，控制哪些信息的梯度能回传
• 误差流保护机制：作者在原文明确指出："LSTM使用乘法单元(MUs)来保护错误流免受不必要的扰动"
• 加法会破坏梯度稳定性：加法会导致梯度叠加而非选择性保留，无法解决传统RNN的梯度消失问题

二、原始论文的设计思路

1. 从"恒定误差循环"(CEC)理论推导出门控需求

LSTM的核心创新是细胞状态(cell state)的设计，它像"传送带"一样让信息在序列中稳定传递。作者发现：

• 若要实现长期依赖 (跨越1000+时间步)，必须让误差信号能恒定流动，不被权重矩阵放大或缩小
• 乘法门控能精确控制误差流：打开(1)时允许误差通过，关闭(0)时阻止扰动
• 这一设计直接解决了传统RNN因权重矩阵连乘导致的梯度消失/爆炸问题

2. 门控设计的演进过程

从原始论文的思路来看，乘法门控是系统性推导的结果：

设计目标	解决方案	为何选择乘法
控制旧记忆保留量	遗忘门(f_t)	乘法实现"保留部分旧信息"，加法会完全改变信息内容
控制新信息写入量	输入门(i_t)	乘法让新候选记忆(C̃_t)按比例融入，加法会导致信息混杂
控制输出信息筛选	输出门(o_t)	乘法让隐藏状态(h_t)只输出相关信息，加法会泄露无关内容

三、实验验证与对比分析

1. 原始论文中的实验验证

虽然论文未详细描述"尝试多种门控方式"的过程，但明确报告了LSTM在多项复杂任务上的突破性表现：

• 人工长期依赖任务：LSTM能学习跨越1000+时间步的依赖关系，这是当时其他RNN无法完成的
• 序列记忆任务：能在最小延迟T/2时间步内存储连续值而不显著退化
• 与传统RNN对比："LSTM outperforms them, and also learns to solve complex, artificial tasks no other recurrent net algorithm has solved"

2. 后续研究的验证与变体

学术界对LSTM门控机制的研究表明：

• GRU变体 ：将遗忘门和输入门合并为"更新门"，但仍保留乘法门控本质，证明乘法是门控机制的核心
• ConvLSTM ：在空间数据处理中用卷积替代全连接，但门控操作仍保留乘法，说明乘法是门控的最佳选择
• 减法门控等变体虽有研究，但性能普遍不如乘法门控，证明乘法的选择有其必然性

四、总结：乘法选择的必然性

LSTM作者选择乘法门控是理论设计+实验验证的结果，而非偶然灵感：

1. 数学本质契合 ：乘法是实现"门控"概念(0-1控制)的唯一自然选择，加法适合信息叠加，卷积适合空间特征提取，均不适用于时序信息筛选

2. 梯度控制必需：乘法直接作用于梯度流，实现LSTM的核心使命------解决长期依赖问题，这是加法等操作无法实现的

3. 效率与简洁：乘法运算在计算图中实现简单高效，适合时序模型的实时处理需求

实验证明：自1997年提出以来，LSTM的乘法门控结构经受住了时间和各种复杂任务的考验，成为序列建模领域的标准架构。即使后续出现GRU等变体，也都保留了乘法门控的核心思想，这是对原始设计正确性的最强证明。