线性代数 - 奇异值分解(SVD Singular Value Decomposition)- 计算顺序 旋转→拉伸→旋转
flyfish
线性代数 - 正交矩阵
线性代数 - 矩阵求逆
线性代数 - 奇异值分解(SVD Singular Value Decomposition)
线性代数 - 奇异值分解(SVD Singular Value Decomposition)- 奇异值在哪里
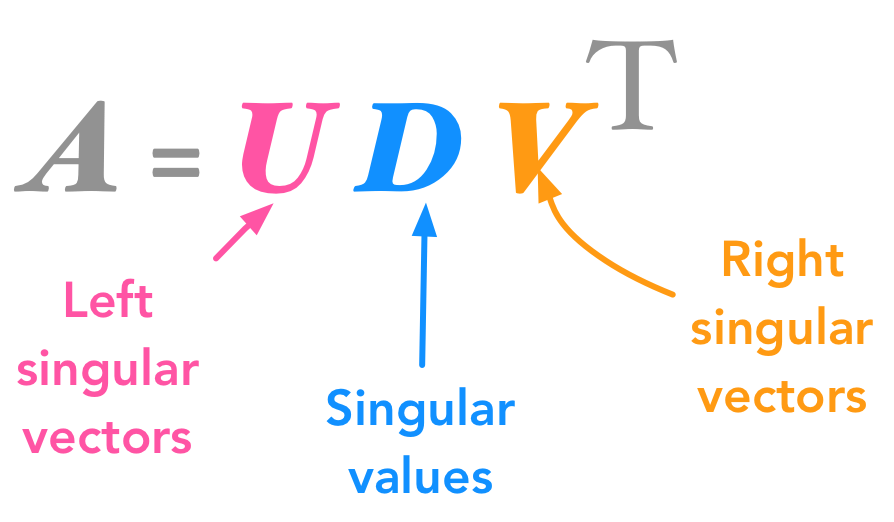
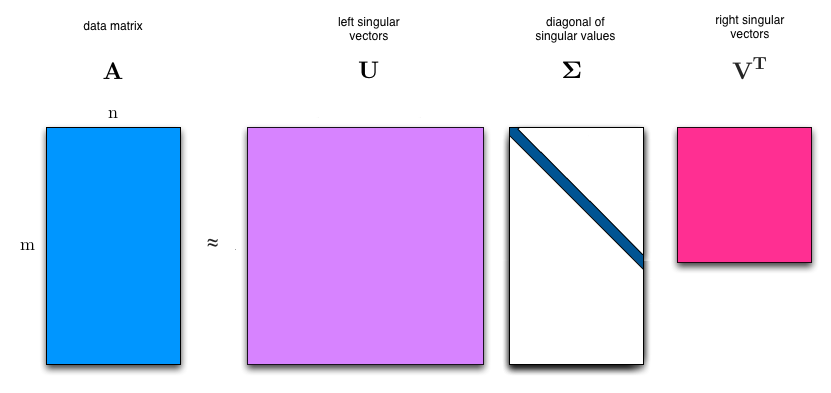
每一个矩阵都可以被视为一个线性变换。
矩阵是线性变换的载体,而线性变换的是对向量的操作,矩阵 A \mathbf{A} A 本身是"所有向量变换规则的集合"
当我们把矩阵 A \mathbf{A} A 看作线性变换 时,它的作用对象是向量(比如空间中的一个点、一条数据)。
输入向量 v \mathbf{v} v → 被 V T \mathbf{V}^T VT 旋转 → 被 Σ \boxed{\mathbf{\Sigma}} Σ 拉伸 → 被 U \mathbf{U} U 旋转 → 输出 A v \mathbf{A}\mathbf{v} Av。
对于公式 A = U Σ V T \mathbf{A} = \mathbf{U} \boxed{\mathbf{\Sigma}} \mathbf{V}^T A=UΣVT,当它作用于向量 v \mathbf{v} v 时,根据矩阵乘法的结合律 ,有:
A v = ( U Σ V T ) v = U ( Σ ( V T v ) ) \mathbf{A}\mathbf{v} = \left( \mathbf{U} \boxed{\mathbf{\Sigma}} \mathbf{V}^T \right) \mathbf{v} = \mathbf{U} \left( \boxed{\mathbf{\Sigma}} \left( \mathbf{V}^T \mathbf{v} \right) \right) Av=(UΣVT)v=U(Σ(VTv))
顺序是:
向量 v \mathbf{v} v 先被最右边的 V T \mathbf{V}^T VT 旋转 ;
再被中间的 Σ \boxed{\mathbf{\Sigma}} Σ 拉伸;
最后被最左边的 U \mathbf{U} U 旋转。
这种"从右到左作用于向量"的规则,和公式中" U \mathbf{U} U 在最左边"的书写顺序是完全一致的------因为矩阵乘法是右结合的(先算最右边的矩阵与向量的乘积,再依次向左结合)。
举个具体例子
A = [ 1 2 2 4 ] \mathbf{A} = \begin{bmatrix} 1 & 2 \\ 2 & 4 \end{bmatrix} A=[1224]:
设向量 v = [ 1 0 ] \mathbf{v} = \begin{bmatrix} 1 \\ 0 \end{bmatrix} v=[10],直接计算 A v \mathbf{A}\mathbf{v} Av:
A v = [ 1 2 2 4 ] [ 1 0 ] = [ 1 2 ] \mathbf{A}\mathbf{v} = \begin{bmatrix} 1 & 2 \\ 2 & 4 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 1 \\ 2 \end{bmatrix} Av=[1224][10]=[12]
用SVD分解步骤计算( U = 1 5 [ 1 2 2 − 1 ] \mathbf{U} = \frac{1}{\sqrt{5}} \begin{bmatrix} 1 & 2 \\ 2 & -1 \end{bmatrix} U=5 1[122−1], Σ = [ 5 0 0 0 ] \boxed{\mathbf{\Sigma}} = \begin{bmatrix} 5 & 0 \\ 0 & 0 \end{bmatrix} Σ=[5000], V T = 1 5 [ 1 2 2 − 1 ] \mathbf{V}^T = \frac{1}{\sqrt{5}} \begin{bmatrix} 1 & 2 \\ 2 & -1 \end{bmatrix} VT=5 1[122−1]):
- 先算 V T v \mathbf{V}^T \mathbf{v} VTv:
V T v = 1 5 [ 1 2 2 − 1 ] [ 1 0 ] = 1 5 [ 1 2 ] \mathbf{V}^T \mathbf{v} = \frac{1}{\sqrt{5}} \begin{bmatrix} 1 & 2 \\ 2 & -1 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \frac{1}{\sqrt{5}} \begin{bmatrix} 1 \\ 2 \end{bmatrix} VTv=5 1[122−1][10]=5 1[12] - 再算 Σ ( V T v ) \boxed{\mathbf{\Sigma}} \left( \mathbf{V}^T \mathbf{v} \right) Σ(VTv):
Σ ( V T v ) = [ 5 0 0 0 ] × 1 5 [ 1 2 ] = 5 5 [ 1 0 ] = 5 [ 1 0 ] \boxed{\mathbf{\Sigma}} \left( \mathbf{V}^T \mathbf{v} \right) = \begin{bmatrix} 5 & 0 \\ 0 & 0 \end{bmatrix} \times \frac{1}{\sqrt{5}} \begin{bmatrix} 1 \\ 2 \end{bmatrix} = \frac{5}{\sqrt{5}} \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \sqrt{5} \begin{bmatrix} 1 \\ 0 \end{bmatrix} Σ(VTv)=[5000]×5 1[12]=5 5[10]=5 [10] - 最后算 U × \mathbf{U} \times U× 上一步结果:
U × 5 [ 1 0 ] = 1 5 [ 1 2 2 − 1 ] × 5 [ 1 0 ] = [ 1 2 ] \mathbf{U} \times \sqrt{5} \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \frac{1}{\sqrt{5}} \begin{bmatrix} 1 & 2 \\ 2 & -1 \end{bmatrix} \times \sqrt{5} \begin{bmatrix} 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 1 \\ 2 \end{bmatrix} U×5 [10]=5 1[122−1]×5 [10]=[12]
结果和直接计算 A v \mathbf{A}\mathbf{v} Av 完全一致,U在最左边,向量先被 V T V^T VT作用的逻辑是自洽的------因为矩阵乘法的结合律保证了顺序的一致性。对任意矩阵 A、B、C(满足乘法维度要求),有 (A×B)×C = A×(B×C)。不管先算前两个矩阵的乘积,还是先算后两个,最终结果完全一样