图论专题(二十五)：最小生成树(MST)——用最少的钱，连通整个世界「连接所有点的最小费用」

哈喽各位，我是前端小L。

欢迎来到我们的图论专题第二十五篇！想象一下，你是城市的规划师，要在几座城市之间修建高速公路，或者在几个服务器之间铺设光纤。你的目标是：

连通性：任何两个点之间都要能到达。
最小成本：所有修建的路线总长度（费用）之和要最小。

这种结构，在图论中被称为**"最小生成树"**。它是一棵树（没有环，边数最少），且包含了所有顶点，且总权值最小。

今天，我们将用Kruskal 算法 来解决这个问题。它的核心逻辑简单得令人发指："只选最便宜的边，只要不形成环！"

力扣 1584. 连接所有点的最小费用

https://leetcode.cn/problems/min-cost-to-connect-all-points/

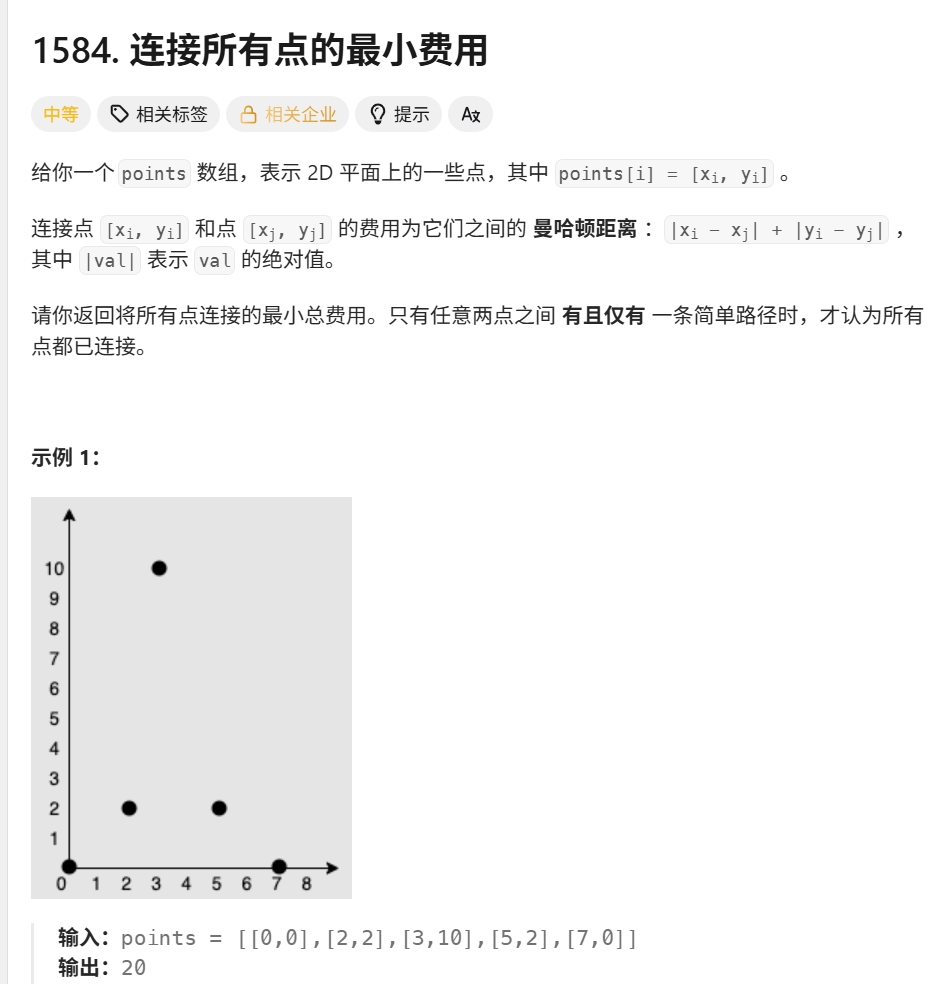
题目分析：

输入：points 数组，表示二维平面上点的坐标 [xi, yi]。
距离：两点之间的连接费用是它们的曼哈顿距离 |xi - xj| + |yi - yj|。
目标：连接所有点，使得总费用最小。

核心模型：

这是一个完全图（Complete Graph），任意两点之间都可以连线。我们需要从中选出 n-1 条边，构成一棵最小生成树。

解决方案：Kruskal 算法 (基于并查集)

Kruskal 算法是贪心思想的完美体现。

策略：我们把所有可能的边，按费用从低到高排序。然后依序尝试把这些边加入我们的网络。

核心判断：对于当前这条边 (u, v)，如果 u 和 v 已经在同一个连通分量里了（即它们已经通过之前的便宜边连通了），那这条边就是多余的（会形成环），我们跳过它。如果它们还不在一个分量里，我们就选用这条边，并把它们 Union 起来。

算法流程：

生成所有边：
- 计算任意两点 i 和 j 之间的曼哈顿距离。
- 将边存储为 (cost, i, j) 的三元组列表。
- (注意：对于 N 个点，会有 N*(N-1)/2 条边。本题 N <= 1000，边数约 50万，排序没问题。)
排序：
- 将所有边按 cost 从小到大排序。
Kruskal 主循环 (并查集登场)：
- 初始化并查集 uf。
- 遍历排序后的边：
  - 对于边 (cost, u, v)：
  - if (uf.find(u) != uf.find(v))：
    - 连通！ uf.union(u, v)。
    - totalCost += cost。
    - edgesCount++。
  - if (edgesCount == n - 1)：树已建成，提前结束。
返回 totalCost。

代码实现 (Kruskal)

C++

复制代码

#include <vector>
#include <cmath>
#include <algorithm>
#include <numeric>

using namespace std;

// --- 并查集模板 ---
class UnionFind {
public:
    vector<int> parent;
    UnionFind(int n) {
        parent.resize(n);
        iota(parent.begin(), parent.end(), 0);
    }
    int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }
    bool unite(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
            parent[rootX] = rootY;
            return true; // 合并成功
        }
        return false; // 已经在同一个集合，无需合并
    }
};

struct Edge {
    int u, v, cost;
    // 重载 < 运算符，方便排序
    bool operator<(const Edge& other) const {
        return cost < other.cost;
    }
};

class Solution {
public:
    int minCostConnectPoints(vector<vector<int>>& points) {
        int n = points.size();
        vector<Edge> edges;

        // 1. 生成所有边 (稠密图：任意两点都有边)
        for (int i = 0; i < n; ++i) {
            for (int j = i + 1; j < n; ++j) {
                int dist = abs(points[i][0] - points[j][0]) + 
                           abs(points[i][1] - points[j][1]);
                edges.push_back({i, j, dist});
            }
        }

        // 2. 排序 (贪心核心)
        sort(edges.begin(), edges.end());

        // 3. Kruskal 算法
        UnionFind uf(n);
        int totalCost = 0;
        int edgesConnected = 0;

        for (const auto& edge : edges) {
            // 尝试连接 u 和 v
            if (uf.unite(edge.u, edge.v)) {
                totalCost += edge.cost;
                edgesConnected++;
                // 优化：只需要 n-1 条边
                if (edgesConnected == n - 1) {
                    break;
                }
            }
        }

        return totalCost;
    }
};

进阶思考：稠密图的更优解 ------ Prim 算法

虽然 Kruskal 算法逻辑清晰，非常适合稀疏图（边少）。但本题是一个完全图（稠密图），边数 $E \\approx V\^2$ 。

Kruskal 的瓶颈在排序： $O(E \\log E) \\approx O(V\^2 \\log V)$ 。
Prim 算法 ：基于节点扩展，类似 Dijkstra。每次找离当前生成树最近的一个节点加入。如果不使用堆，直接用数组扫描，复杂度为 $O(V\^2)$ 。

在 $N=1000$ 的情况下，Prim ( $10\^6$ ) 会比 Kruskal ( $10\^6 \\times \\log 10\^6 \\approx 2 \\cdot 10\^7$ ) 快不少。

(虽然 Kruskal 能过，但 Prim 是更"专业"的选择。)

Prim 算法简述 (数组版)：

dist[i] 记录节点 i 到当前生成树 的最小距离。初始化为 $\\infty$ ，dist[0]=0。
循环 n 次：
- 找到当前未访问节点中 dist 最小的节点 u。
- 将 u 标记为已访问，加入生成树，累加 dist[u]。
- 松弛：用 u 去更新所有未访问邻居 v 的 dist[v]：dist[v] = min(dist[v], weight(u, v))。

总结：图论世界的"基建工程"

今天，我们攻克了图论中最经典的"最小生成树"问题。

并查集 是 Kruskal 算法的灵魂，它高效地帮我们判断了"是否形成环"。
贪心是 MST 的核心，无论是 Kruskal（选最小边）还是 Prim（选最近点），都在贯彻这一思想。

至此，我们结束了"并查集"篇章。从下一篇开始，我们将进入图论的终极篇章------经典算法 。我们将挑战 Dijkstra ，去解决比 MST 更复杂的"带权最短路径"问题。

下期见！