图论专题(十九)：DAG上的“关键路径”——极限规划「并行课程 III」

哈喽各位，我是前端小L。

欢迎来到我们的图论专题第十九篇！之前的课程表问题，每门课似乎只是一个"节点"，瞬间就能修完。但在现实中，每门课都有时长。

如果 A (3个月) 和 B (5个月) 都是 C (2个月) 的先修课。哪怕我们可以同时修 A 和 B，我们最早什么时候能修完 C？

A 修完：第3个月。
B 修完：第5个月。
必须等最慢的那门先修课（B）结束，C 才能开始。
所以 C 完成的时间 = max(3, 5) + 2 = 7 个月。

这个简单的逻辑告诉我们：一个节点的最早完成时间，取决于它所有前驱节点中，完成时间最晚的那个。

力扣 2050. 并行课程 III

https://leetcode.cn/problems/parallel-courses-iii/

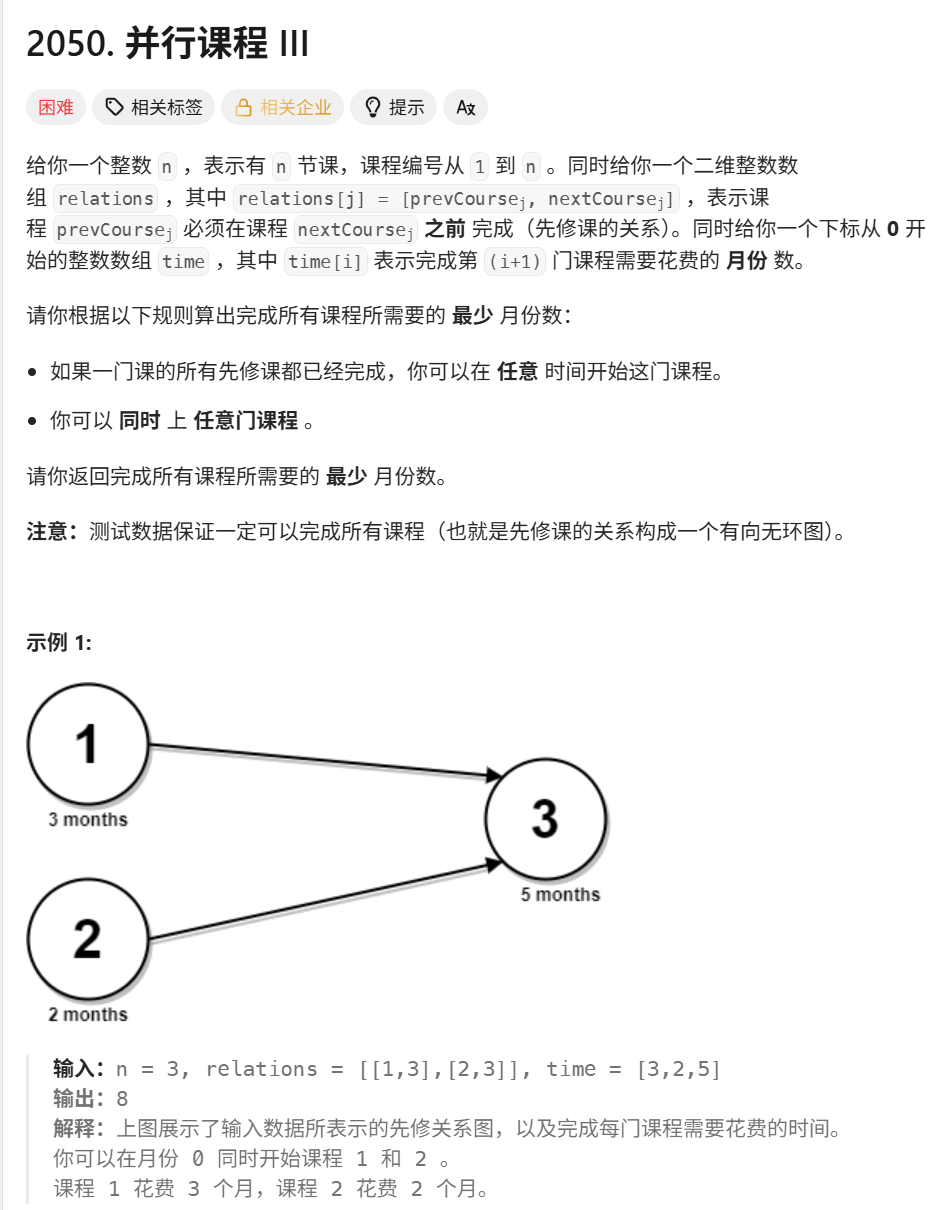
题目分析：

输入：整数 n，依赖关系 relations，每门课的耗时 time 数组。
规则：
1. prevCourse -> nextCourse：必须先修完 prev 才能修 next。
2. 并行：任意数量的无依赖课程可以同时进行。
目标：计算完成所有课程所需的最少月份数。

核心模型转化： 这个问题本质上是在求 DAG（有向无环图）中的最长路径 。为什么是"最长"？因为为了完成所有任务，我们受限于那条耗时最长的依赖链（关键路径）。只有那条链走完了，整个工程才算结束。

解决方案：带 DP 状态的 Kahn 算法

我们依然使用 Kahn 算法（BFS 拓扑排序）的框架，但在遍历过程中，我们需要维护一个状态数组 dist。

1. DP状态定义： dist[i] 表示：课程 i 最早能完成的时间。

2. 状态转移： 当我们要处理课程 u 指向的邻居 v (u -> v) 时：

我们知道 u 已经修完了，耗时 dist[u]。
v 的开始时间，至少要等到 u 结束。
v 完成的时间，至少是 dist[u] + time[v]。
因为 v 可能有多个先修课（x->v, y->v...），v 必须等所有先修课都结束。所以 dist[v] 取所有前驱带来的结果中的最大值 。 dist[v] = max(dist[v], dist[u] + time[v])

算法流程：

建图 & 统计入度：
- 邻接表 adj，入度数组 indegree。
初始化 DP 数组：
- vector<int> dist(n + 1, 0)。
- 对于所有课程 i，初始 dist[i] = time[i-1]。 (假设它没有先修课，完成时间就是它自身的时长)。
寻找起点：
- 将所有 indegree[i] == 0 的课程入队 q。
BFS (拓扑排序 + 状态更新)：
- while (!q.empty()):
  - u = q.front(); q.pop();
  - 遍历 u 的邻居 v：
    - 核心更新 ：dist[v] = max(dist[v], dist[u] + time[v-1])。
    - indegree[v]--。
    - if (indegree[v] == 0)，说明 v 的所有依赖都算完了，dist[v] 已经确定是最终的最早完成时间了，入队。
最终答案：
- 所有课程 dist 中的最大值，就是整个项目的完工时间。
- return *max_element(dist)。

代码实现 (Kahn + DP)

C++

复制代码

#include <vector>
#include <queue>
#include <algorithm>

using namespace std;

class Solution {
public:
    int minimumTime(int n, vector<vector<int>>& relations, vector<int>& time) {
        // 1. 建图 + 统计入度
        vector<vector<int>> adj(n + 1);
        vector<int> indegree(n + 1, 0);
        
        for (const auto& rel : relations) {
            int prev = rel[0];
            int next = rel[1];
            adj[prev].push_back(next);
            indegree[next]++;
        }

        // 2. 初始化 DP 数组
        // dist[i] 表示课程 i 完成的最早时间
        vector<int> dist(n + 1);
        queue<int> q;

        for (int i = 1; i <= n; ++i) {
            // 初始状态：只考虑自身时长
            dist[i] = time[i - 1]; 
            if (indegree[i] == 0) {
                q.push(i);
            }
        }

        // 3. BFS (拓扑排序)
        while (!q.empty()) {
            int u = q.front();
            q.pop();

            for (int v : adj[u]) {
                // 状态转移：v 必须等 u 完成
                dist[v] = max(dist[v], dist[u] + time[v - 1]);
                
                indegree[v]--;
                if (indegree[v] == 0) {
                    q.push(v);
                }
            }
        }

        // 4. 找到所有课程中最后完成的那个时间
        int maxTime = 0;
        for (int i = 1; i <= n; ++i) {
            maxTime = max(maxTime, dist[i]);
        }
        
        return maxTime;
    }
};

深度复杂度分析

V ：课程数 n。
E ：依赖关系数 relations.size()。
时间复杂度 O(V + E)：
- 标准的 Kahn 算法流程。建图 O(E)，每个节点入队出队一次 O(V)，每条边遍历一次 O(E)。
空间复杂度 O(V + E)：
- 邻接表 O(V + E)。
- 辅助数组 dist, indegree, q 均为 O(V)。

总结

今天这道题，展示了拓扑排序在"工程规划"中的核心作用。它不再仅仅是排一个先后顺序，而是结合了简单的动态规划思想，帮我们计算出了并行条件下的最短工期。

核心逻辑链：

并行 -> 互不影响，同时进行。
依赖 -> 必须等待。
等待 -> 取决于最晚结束的前驱 (max)。
总工期 -> 取决于关键路径（最长的那条依赖链）。

到这里，我们对 DAG（有向无环图）的处理能力已经相当成熟了。在下一篇中，我们将进入图论的第五个阶段------并查集 (Union-Find)。这将是一个处理"动态连通性"和"分组"问题的全新、强大的数据结构。准备好迎接"合并"与"查找"的魔法了吗？

下期见！