对于数据结构：堆的超详细保姆级解析—上

开篇介绍：

hello 各位，咱们又见面啦～相信大家看到 "堆" 这个标题，再联想到上一篇咱们刚 "啃完" 的二叉树，心里多少会有点小嘀咕：二叉树都学得晕头转向了，堆又是什么 "厉害角色"？别慌，先给大家吃颗定心丸 ------ 堆其实和二叉树关系紧密，它是完全二叉树的一种经典应用，掌握了二叉树的基础，再学堆，会顺畅很多～

在数据结构的星空中，堆如同一颗明亮的星辰，它的光芒不仅在于高效的操作特性，更在于教会我们以结构化思维剖析问题。掌握它，便是掌握了一种化繁为简的智慧，这种智慧将伴随我们在编程之路上不断探索，解锁更多复杂问题的解决方案，让每一行代码都更具深度与效率。

不过，也先提前打个招呼，堆虽依托于二叉树，但它有自己独特的 "脾气" 和 "玩法"。上一篇咱们从树的概念入手，逐步剖析到二叉树的形态、性质、存储结构，算是把二叉树的 "骨架" 搭好了；而这一篇的堆，就是要在这个 "骨架" 上，填充进 "排序""优先队列" 这些实用的 "血肉"。

回忆一下，上一篇咱们反复强调完全二叉树的顺序存储（用数组）很高效，因为能通过下标快速找到父、子节点。而堆，恰恰就是基于完全二叉树的顺序存储来实现的！它能在 O (log n) 时间复杂度内完成 "插入""删除（取最值）" 等操作，这让堆在 "求 Top K""堆排序""优先队列" 等场景中大放异彩 ------ 比如想从海量数据里找最大的几个数，用堆来做，效率会比普通遍历高得多。

可能有同学会问："堆具体是怎么工作的？和普通二叉树有啥不一样？" 别急，这篇 "超详细保姆级解析 --- 上"，咱们就从堆的定义 和基本性质入手，一步步拆解它的逻辑。咱们会先弄清楚 "大根堆""小根堆" 的区别，再去看堆是如何通过 "向上调整""向下调整" 这些操作，维持自身 "父节点始终大于（或小于）子节点" 的特性。

学习过程中，大家可以结合上一篇里完全二叉树的顺序存储知识，去思考 "堆的数组下标和节点关系"；也可以试着自己画一画堆的结构变化，感受每次调整操作后，堆是如何保持 "有序性" 的。相信我，只要跟着节奏，把堆的底层逻辑捋顺，你会发现它其实是个 "看起来抽象，实则规律很强" 的数据结构～

好啦，话不多说，咱们这就开启堆的学习之旅，一起去探索它的奥秘吧～

堆的介绍：

一般堆使用顺序结构的数组来存储数据，堆是一种特殊的二叉树，具有二叉树的特性的同时，还具备其他的特性。

堆的概念与结构：

如果有一个关键码的集合 K={k0​,k1​,k2​,...,kn−1​}，把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足：Ki​≤K2∗i+1​（Ki​≥K2∗i+1​ 且 Ki​≤K2∗i+2​），、、，则称为小堆（或大堆）。将根结点最大的堆叫做最大堆或大根堆，根结点最小的堆叫做最小堆或小根堆。

1. 堆的存储基础

堆的数据是基于完全二叉树的顺序存储方式 来组织的。也就是说，堆在物理上是一个一维数组，但从逻辑结构上看，它符合完全二叉树的形态，就像下图：

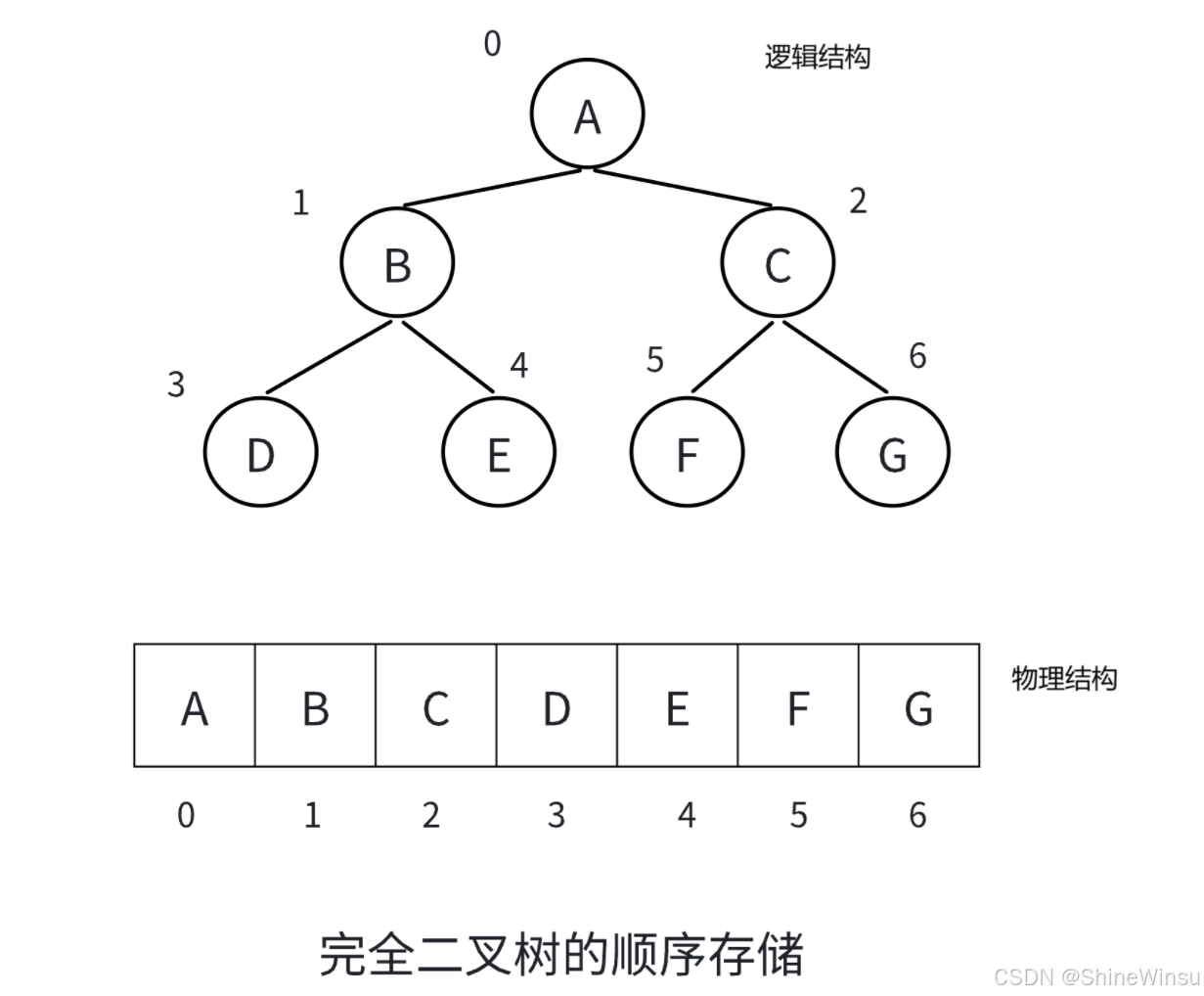
完全二叉树的特点是：除了最后一层，其他层的节点数都达到最大值，且最后一层的节点都集中在左侧连续的位置上。这种存储方式的好处是，不需要额外的指针来表示节点间的父子关系，仅通过数组下标就能快速确定父节点和子节点的位置。

2. 堆的核心规则（以数组下标 i 对应的节点为例）

• 对于小根堆：要求当前节点 Ki 的值小于等于它的左子节点 K2∗i+1 的值（如果左子节点存在）。
• 对于大根堆：要求当前节点 Ki 的值大于等于它的左子节点 K2∗i+1 的值，并且小于等于它的右子节点 K2∗i+2 的值（如果右子节点存在）。这里要注意，大根堆的规则描述里，"Ki≥K2∗i+1 且 Ki≤K2∗i+2" 可能存在表述偏差，更准确的大根堆规则是：父节点的值大于等于其左右子节点的值（即 Ki≥K2∗i+1 且 Ki≥K2∗i+2，当子节点存在时）；小根堆则是父节点的值小于等于其左右子节点的值（即 Ki≤K2∗i+1 且 Ki≤K2∗i+2，当子节点存在时）。

3. 大根堆与小根堆的区分

• 大根堆：整个堆的根节点（也就是数组中下标为 0 的元素，因为完全二叉树顺序存储时根节点对应数组首元素）的值是最大的。这意味着在大根堆中，每次要获取最大值时，直接取根节点即可，非常高效。
• 小根堆：整个堆的根节点的值是最小的。同理，每次要获取最小值时，直接取根节点就行。

这里稍微提个醒，对于大根堆而言，是要求父节点的数据大小大于子节点的数据大小就行，并不要求什么左边子节点数据大小大于右边子节点的数据大小等等，大家这点要注意一下，下面的小跟堆也是一样的道理。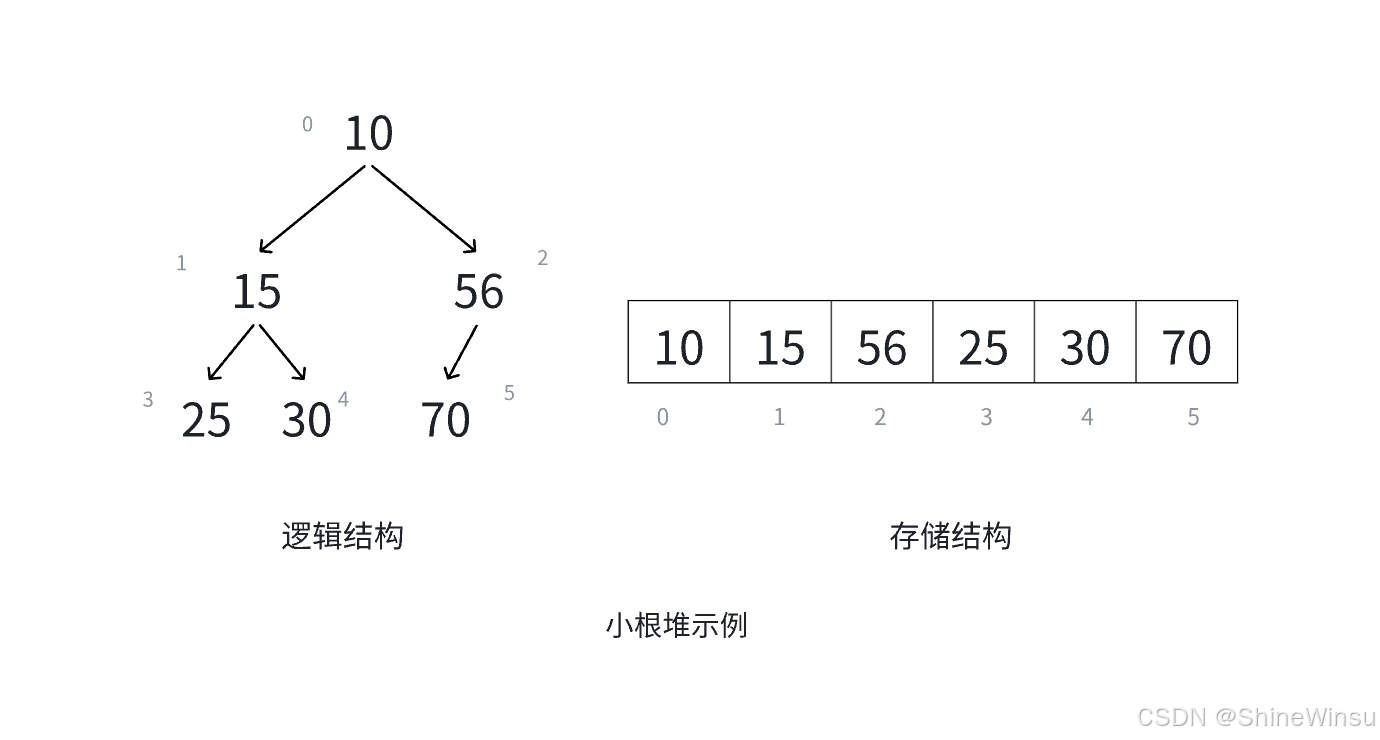

举个例子帮助理解

假设我们有一个小根堆，用数组存储为 [2,5,3,7,6,4]。从逻辑上看，它对应的完全二叉树结构中：

• 根节点是 2（下标 0），它的左子节点是 5（下标 2∗0+1=1），右子节点是 3（下标 2∗0+2=2），满足 2≤5 且 2≤3。
• 下标为 1 的节点 5，它的左子节点是 7（下标 2∗1+1=3），右子节点是 6（下标 2∗1+2=4），满足 5≤7 且 5≤6。
• 下标为 2 的节点 3，它的左子节点是 4（下标 2∗2+1=5），满足 3≤4。

这样的结构就符合小根堆的规则，根节点 2 是整个堆中的最小值。

堆的性质：

堆具有以下性质

• 堆中某个结点的值总是不大于或不小于其父结点的值；
• 堆总是一棵完全二叉树。

如何将堆（二叉树）的节点存储进一维数组的内容中

那么我们知道，堆的本质，其实是算是二叉树，只不过，我们是用一维数组，也就是顺序表的形式去存储数据，那么，也就代表着，我们要把二叉树的某个节点通过某种关系，存储进顺序表中某个下标所对应的小格子里，换句话来说就是，二叉树的每一个节点，都对应着顺序表中的一个下标，再次提醒，我们的这个二叉树，是完全二叉树，最好不要是不委屈二叉树，不难顺序表不能一个挨着一个的放置数据。

那么我们通过上面，可以知道，二叉树的某一个节点，和顺序表的下标，有着某种奇妙的关系，正是这个关系，让我们可以将二叉树的节点存储进顺序表中，换句话来说就是，我们可以同顺序表的下标，来将二叉树体现出来，那么具体要如何做到呢？这与数学有关;
• 对于具有n 个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有结点从0 开始编号，则对于序号为i 的结点有：

1. 若i>0 ， i 位置结点的双亲序号： (i-1)/2 ；
2. i=0 ， i 为根结点编号，无双亲结点
3. 若2i+1<n ，左孩子序号： 2i+1（为奇数 ），2i+1>=n 否则无左孩子
4. 若2i+2<n ，右孩子序号： 2i+2（为偶数）， 2i+2>=n 否则无右孩子

大家一定一定要牢牢记住这几点。

所以也就是，我们要按 从上至下、从左至右的数组顺序对所有结点从0 开始编号，然后依次将二叉树的节点存储进顺序表中所对应的下标（该节点的序号是多少，它所对应的小标就是多少）所对应的小格子。

图示就是这样：

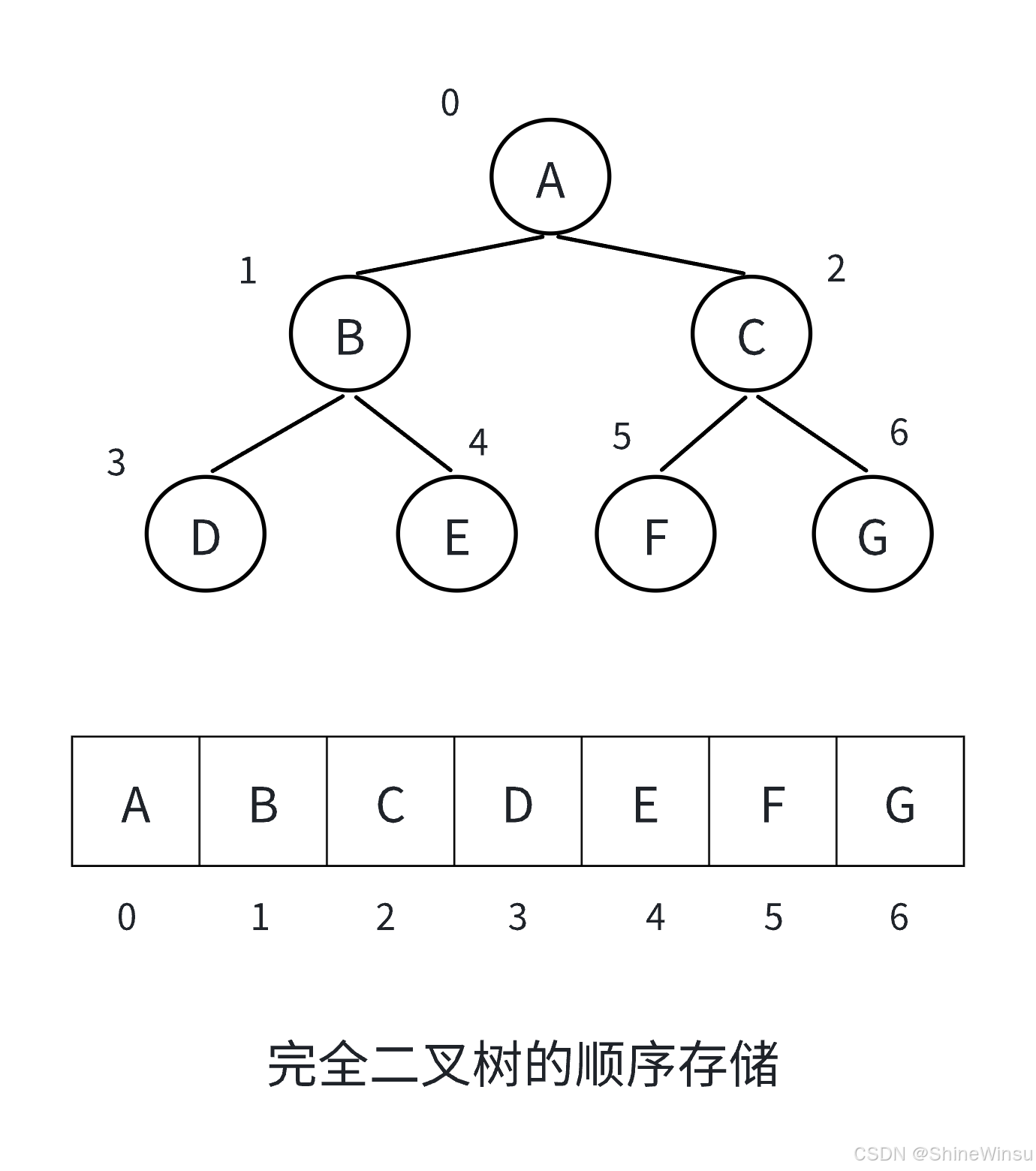
1. 父节点序号规则

完全二叉树顺序存储时，节点按 "从上到下、从左到右" 的顺序存入数组。对于数组中序号为 i 的节点，若 i>0，父节点序号通过 (i−1)/2（整数除法）计算。

• 以节点 B（数组下标 i=1）为例：计算 (1−1)/2=0，得到父节点在数组中的下标为 0，对应节点 A，与图中 B 的父节点是 A 完全一致。
• 再看节点 D（数组下标 i=3）：计算 (3−1)/2=1，父节点下标为 1，对应节点 B，和图中 D 的父节点是 B 相符。
• 当 i=0 时，比如节点 A，它是完全二叉树的根节点，没有父节点，这与图中根节点 A 不存在父节点的情况一致。

2. 左孩子序号规则

若 2i+1<n（n 是完全二叉树的节点总数，此图中 n=7），则序号为 i 的节点的左孩子序号为 2i+1；若 2i+1≥n，说明该节点没有左孩子。

• 节点 A（数组下标 i=0）：计算 2×0+1=1，1<7，所以左孩子序号为 1，对应节点 B，图中 A 的左孩子正是 B。
• 节点 C（数组下标 i=2）：计算 2×2+1=5，5<7，左孩子序号为 5，对应节点 F，与图中 C 的左孩子是 F 一致。

3. 右孩子序号规则

若 2i+2<n，则序号为 i 的节点的右孩子序号为 2i+2；若 2i+2≥n，该节点没有右孩子。

• 节点 A（数组下标 i=0）：计算 2×0+2=2，2<7，右孩子序号为 2，对应节点 C，图中 A 的右孩子为 C。
• 节点 C（数组下标 i=2）：计算 2×2+2=6，6<7，右孩子序号为 6，对应节点 G，和图中 C 的右孩子是 G 相符。

这三条规则的重要性在于，在完全二叉树的顺序存储结构中，不需要额外的指针（如链表中的左右指针）来记录节点间的父子关系，仅通过简单的数学计算，就能快速确定任意节点的父节点、左孩子和右孩子。这种特性使得完全二叉树的顺序存储非常高效，也为后续堆（一种基于完全二叉树的特殊数据结构）的实现和操作（如堆的调整）提供了便利的基础。

再次提醒大家，无论如何，都要把上面所说的规律给它吃透并熟记，一定一定。

那么接下来，我们就可以开始着手实现我们的堆了。

实现堆所需步骤：

一如既往，我们已经知道了，其实堆的本质就是数组，所以堆所用的结构，我在这里就不赘述，大家参考顺序表的结构创建即可，一模一样。

//堆底层结构为数组，因此定义堆的结构为
//因为堆是用来表示完全二叉树
//所以，我们是用顺序表，也就是数组结构去实现堆
//换句话来说就是，我们要把完全二叉树中的
//每一个节点（有对应的序号）存储进数组的对应的小标的格子中
//所以，我们依旧是需要定义一个顺序表，也就是数组结构
//和之前所学的顺序表结构类似

typedef int name1;

struct heap
{
	name1* arr;
	int size;
	int capacity;
};

typedef struct heap hp;

我们直接看实现堆所需要的步骤有哪些：

1. 堆的初始化

• 功能：初始化堆结构体，设置初始状态（空堆）。

2. 堆的销毁

• 功能：释放堆占用的内存，避免内存泄漏。

3. 核心调整算法

堆的核心是维护 "父节点值 ≤ 子节点值"（小堆）的特性，依赖两个调整算法：

（1）向上调整算法（adjustup）

• 适用场景：插入元素后，修复堆的特性（从新插入的叶子节点向上调整）。

（2）向下调整算法（adjustdown）

• 适用场景：删除堆顶元素后，修复堆的特性（从新的堆顶向下调整）。
• 前提：被调整节点的左右子树已满足堆特性。

4. 元素插入（hpinsert）

• 功能：在堆的末尾插入新元素，并通过向上调整维持堆特性。

5. 堆顶元素删除（hppop）

• 功能：删除堆顶元素（最小值），并通过向下调整维持堆特性。

6. 其他辅助操作

• 获取堆顶元素并删除（hptop） ：返回堆顶元素后，调用hppop删除。
• 判断堆是否为空（hpempty） ：通过size == 0判断。
• 获取堆大小（hpsize） ：直接返回size。
• 交换元素（swapdata）：通过指针交换两个元素的值（辅助调整算法）。

实现堆的核心是维护堆的特性，依赖向上 / 向下调整算法。关键步骤可概括为：

1. 定义堆结构（数组、大小、容量）。
2. 实现初始化与销毁，管理内存。
3. 实现向上 / 向下调整算法，确保堆特性。
4. 基于调整算法实现插入、删除等操作。

通过这些步骤，我们便可完整实现一个功能完善的小堆，支持元素的插入、删除、获取堆顶等操作。

那么接下来，就让我们逐步拆解实现堆所需的各个步骤吧。

对堆的初始化和销毁

简单，真的简单，我们知道，其实堆的物理结构就是数组，只是我们脑子里要想成二叉树结构，但是归根结底来说，堆的各个数据，还是存储在数组中，我们上面的堆的结构和顺序表的结构一样也可以说明这一点。

那么同样的道理，对于堆的初始化和销毁，不就相当于也是对数组（顺序表）的初始化和销毁吗，那么这一部分，我们的顺序表中可是讲的不能再清楚了，大家可以移步这里：对于数据结构：顺序表的超详细保姆级解析_链表的内容对应的地址越界-CSDN博客

我这边就直接给出代码供大家参考：

//对堆的初始化
void hpinit(hp* php)
{
	assert(php);
	php->arr = NULL;
	php->size = 0;
	php->capacity = 0;
}

//对堆的销毁
void hpbreak(hp* php)
{
	assert(php);
	free(php->arr);
	php->arr = NULL;
	php->size = 0;
	php->capacity = 0;
}

判断堆是否为空以及统计堆的数据个数：

easy，really easy，各位，这不还是和我们的顺序表息息相关吗，甚至我们之前的栈，不就讲到了这一部分吗，我滴妈，太简单了诸位，我直接甩出一个完整代码，大家要是不知道的，欢迎移步讲解栈的那一篇博客。

//求堆中数据的个数
int hpsize(hp* php)
{
	assert(php);
	//和顺序表差不多，我们直接返回size就行
	return php->size;
}

//判断堆是否为空
bool hpempty(hp* php)
{
	if (php->size == 0)
	{
		return true;
	}
	else
	{
		return false;
	}
}

OK，轻松而无趣的部分到这里就差不多结束了，接下来，才是我们堆真正的难点所在~~~~~，前方高能，请大家抓好扶手。

对于堆的插入数据

OK，作为一个合格的数据结构，怎么可能能少了插入数据这么一个不可或缺的功能呢？

那么，对于堆的插入数据，我们又要如何实现呢？

大家可千万不要搁那，啊我想，我想，我想想想，得了吧，除非天赋异禀，不难想个蛋蛋出来~。

我在这边就直接告诉大家方法。

首先，我们肯定知道的是，我们的堆，本质就是数组结构，那么大家不妨想一想，我们数组结构的一个巨大无比的优势是什么嘞？就比如说，是什么让我们实现栈的时候，不用单向链表，而是去使用顺序表，也就是数组结构呢？大家快回忆回忆。

诶对了，聪明的你很快就能想到，数组的一个天然的巨大优势就是，它的尾插数据，非常的方便以及高效。

那么知道了这一点，其实我们对堆（数组）的插入数据这一个步骤，有了方法，既然数组的尾插无比好使，而我们的堆本质又是数组，那么那么，我们对堆的数据插入，也用尾插呗，是的各位，就是这样子，我们对堆的数据插入，也是用尾插进去，就是和顺序表的尾插一模一样 如出一辙～

大家可以看下图进行理解，其实是很简单的

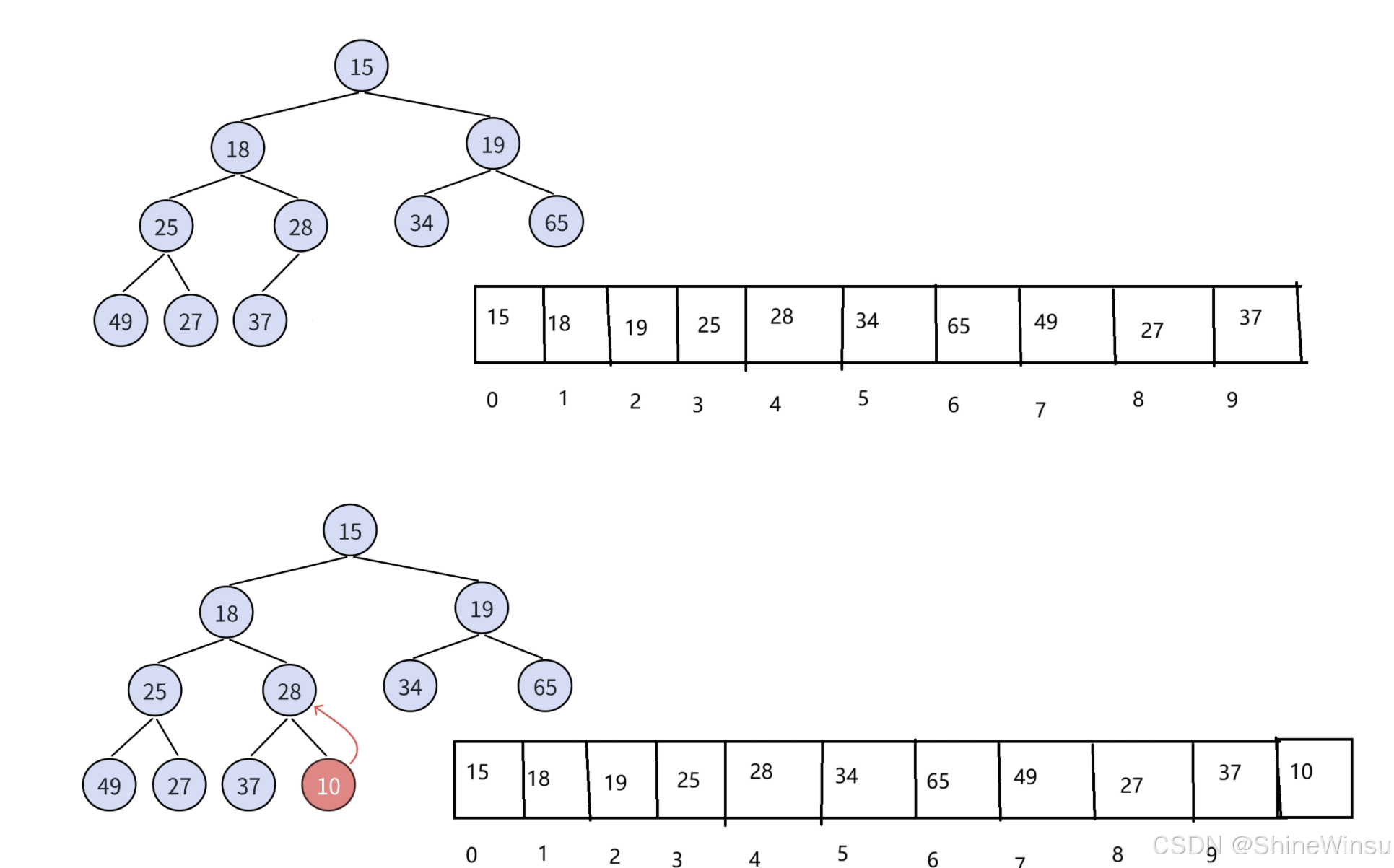
详细代码如下：

//对堆的插入数据
void hpinsert(hp* php, name1 x)
{
	assert(php);

	//其实就是我们直接把数据插进数组（堆）的最后
	//换句话来说就是对数组的尾插
	//但是呢，在尾插之后
	//我们是需要通过向上调整算法去将堆的数据结构安排好
	//比如小堆就是要满足父节点小于等于子节点

	//老样子，先判断数组剩余空间够不够
	if (php->size == php->capacity)
	{
		int newcapacity = php->capacity == 0 ? 2 : 2 * php->capacity;
		name1* temp = (name1*)realloc(php->arr, sizeof(name1) * newcapacity);
		if (temp == NULL)
		{
			perror("malloc false:");
			exit(1);
		}
		//记得有借有还
		php->arr = temp;
		php->capacity = newcapacity;
	}
	//进行尾插：
	php->arr[php->size] = x;
	php->size++;

	//进行向上调整算法
	adjustup(php->arr, php->size - 1);
}

那么，用类似顺序表尾插的方式，对我们的堆插入了数据之后，就这么结束了吗？nonono，用头发想都知道，堆诶，二叉树诶，怎么可能就这么简单，所以呢，在我们利用尾插，去对堆插入了数据之后，我们接着就要对堆，进行数据顺序的改正。

为什么要进行顺序改正呢？因为我们知道，我们对于小堆和大堆，父节点和子节点的数据大小，是有严格要求的，那么这里我们假设是我们要实现小堆，那么大家看看上图，插入了10这个子节点之后，这个堆（二叉树），还符合小堆的要求吗？肯定不符合的。

所以，我们就要进行顺序修正，而对于插入数据的堆的顺序修正，就要用到，向上调整算法，也就是上面代码的adjustup函数。

向上调整算法：

OiOi大家，竖起耳朵，睁大眼睛，堆的第一个小难点来了。

就是我们的向上调整算法，三十年经验，三秒教给大家。

向上调整算法，就是针对我们对堆插入时，也就是插入二叉树中最下面的一个子节点，因为有可能加入了这个新的子节点之后，新堆的数据就不符合我们的小堆or大堆的概念，所以，我们就得通过向上调整算法去进行将新形成的堆变为符合小堆or大堆的要求的堆。

那么，向上调整法，究竟是个什么东西，我们又要如何实现呢？

💡 向上调整算法
• 先将元素插入到堆的末尾,即最后一个孩子之后
• 插入之后如果堆的性质遭到破坏，将新插入结点顺着其双双亲往上调整到合适位置即可

向上调整算法是堆插入操作的核心支撑，其设计完全围绕 "修复堆特性" 展开。以下从原理、执行流程、细节设计和示例验证四个维度进行极致详细的解析：

一、算法本质与适用场景

本质 ：通过 "自底向上" 的比较交换，将破坏堆特性的节点移动到正确位置，最终恢复 "父节点值 ≤ 子节点值"（小堆）的核心性质。适用场景 ：仅用于堆的插入操作------ 当新元素被添加到堆的末尾（数组最后一位）后，可能破坏堆的层级关系，此时需通过该算法修复。

二、核心原理：完全二叉树的父子关系

堆的底层是完全二叉树，其节点在数组中的存储具有严格的数学关系：

• 若子节点下标为 child，则其父节点下标为 parent = (child - 1) // 2（整数除法）。例：子节点下标为 5 → 父节点下标 (5-1)/2=2；子节点下标为 4 → 父节点下标 (4-1)/2=1。
• 这种关系是向上调整的 "导航系统"，确保每次都能准确定位父节点。

三、执行流程（以小堆为例）

假设新元素插入到数组下标 child 处，算法执行步骤如下：

1. 循环条件：child > 0

• 当 child = 0 时，该节点已是根节点（无父节点），调整终止。
• 循环的目的：持续向上追溯，直到找到新元素的正确位置。

2. 定位父节点

计算当前子节点的父节点下标：parent = (child - 1) // 2。

3. 比较与交换

• 若父节点值 > 子节点值 （违反小堆特性）：
  • 交换父子节点的值（swapdata），此时新元素移动到父节点位置。
  • 更新 child = parent（新元素的位置上移，继续向上比较）。
• 若父节点值 ≤ 子节点值 （符合小堆特性）：
  • 无需继续调整，直接退出循环。

四、关键细节设计

1. **为什么从子节点向上调整？**新元素插入在堆的末尾（叶子节点），仅可能影响其祖先节点的堆特性，无需检查其他分支，效率更高。

2. 为什么循环条件是 child > 0？ 根节点（child=0）没有父节点，此时调整已无意义，必须终止。

3. 交换后为何更新 child = parent？ 新元素通过交换移动到了父节点位置，下一步需要与新的父节点（即原父节点的父节点）比较，因此子节点的位置需要同步上移。

4. 时间复杂度：O (log n) 最多需要调整的次数等于树的高度，对于包含 n 个节点的完全二叉树，高度为 log₂n（向上取整），因此时间复杂度为对数级。

   //向上调整算法：
   //先将元素插入到堆的末尾, 即最后一个孩子之后
   //插入之后如果堆的性质遭到破坏，将新插入结点顺着其双双亲往上调整到合适位置即可

   //我们肯定要借助循环去不断将最后插入的子节点
   //去与它的祖先一一比较
   //而且由于我们是实现小堆
   //所以就要求父节点的数据要小于子节点的数据大小
   //所以我们就要比较
   //一旦子节点小于父节点
   //就要把这两个节点给交换
   //这边注意，我们不仅要将这两个节点数据进行交换
   //我们还要把parent和child进行交换，看到下面的代码就能理解
   //就相当于是儿子和父亲互换了
   //原本的儿子成了爸爸，而原来的爸爸成了儿子

   //那么我们的循环条件是什么呢？
   //其实就是当我们的child大于0的时候，就进行循环
   //而一旦child到了0，我们知道，0其实就代表是根节点
   //是所有节点的祖先
   //那么child都干到了祖先，还能和什么父节点进行比较呢？

大家可以根据上面这段话理解理解，其实就是我们要将新插入的子节点，去和它的祖先不断比较，看一模一符合我们的小堆or大堆的特征，祖先就是这些：

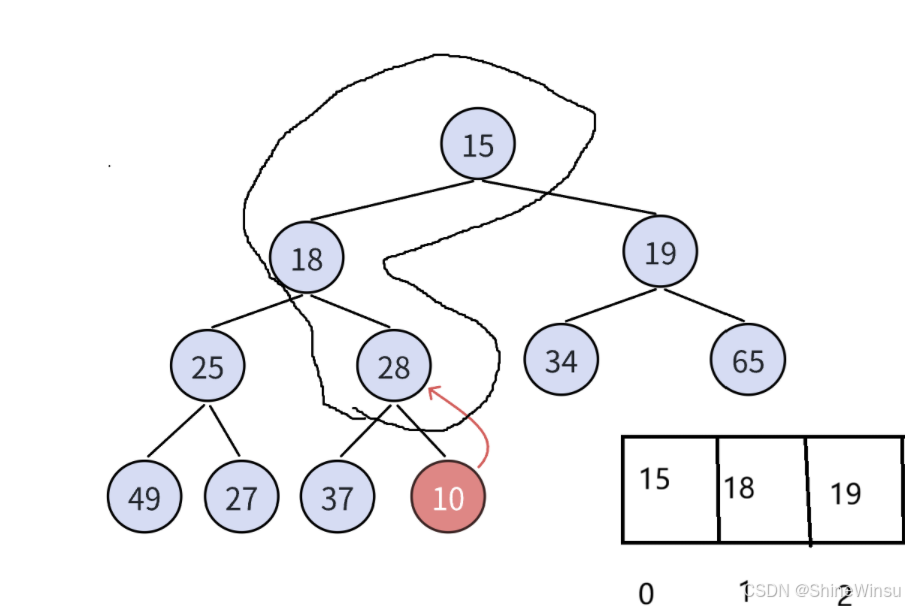
我们就是要不断进行比较，拿小堆来说，如果有儿子比爸爸小的，就得把这两个进行交换，不仅是数据交换，也是各自下标的交换哦。

然后再去比较原本的儿子的爷爷，也就是新的节点的父节点，直到移动到了根节点，那就得停止了，因为根节点可没有父节点。

下面就是我们循环的详细代码：

	while (child > 0)
	{
		//先通过数学关系找到子节点的父节点
		int parent = (child - 1) / 2;
		
		//比较子节点和父节点的数据大小
		//因为是小堆，所以就要求父节点数据小于子节点的数据
		
		//所以当我们发现子节点数据大小小于父节点数据
		//我们就得对调身份
		if (arr[parent] > arr[child])
		{
			//将子节点和父节点的数据进行交换
			swapdata(&arr[parent], &arr[child]);

			//child和parent二者本身也得交换
			//毕竟是原本的儿子成了爸爸，而原来的爸爸成了儿子
			child = parent;

			//接下来就得去和最开始的子节点的下一个祖先进行比较
			//所以这也是我们什么为什么要让child = parent
			//就是为了能不断找到子节点的祖先
			parent = (child - 1) / 2;
		}
		else//当子节点和其父节点数据大小满足小堆的要求时，我们就直接退出循环
		{
			break;
		}
	}

下面是详细解析：

我先说明一下向上调整算法函数的两个参数，有什么意义：

//针对向上调整算法的两个参数
//第一个参数自然就得得是我们的堆的数组
//而第二个参数，由于我们是尾插，那么就代表其实前面的数据的顺序都是OK的
//就这最后一个插入的数据需要与前面的父节点（祖先）进行比较
//并根据是小堆还是大堆来进行数据的交换

//这边也需要知道，我们的数组的最后一个有效数据
//在数组中所对应的下标是php->size - 1
//因为我们知道，数组是从0开始存储的
void adjustup(name1* a,int child);

这段代码是小堆向上调整算法的核心实现，每一行都围绕 "修复堆特性" 展开，需要结合 "完全二叉树的父子关系" 和 "小堆的定义" 来理解。下面逐行拆解逻辑，结合原理和示例讲清每一步的作用：

一、整体逻辑前提

先明确两个关键背景，这是理解代码的基础：

1. 小堆的定义：任意父节点的值 ≤ 其左右子节点的值（核心是 "父小，子大"）。
2. 完全二叉树的父子下标关系 ：若子节点下标为 child，则父节点下标必为 (child - 1) / 2（整数除法，无论左 / 右子节点都适用）。例：左子节点下标 = 3 → 父节点 =(3-1)/2=1；右子节点下标 = 4 → 父节点 =(4-1)/2=1（和左子节点同父）。

二、逐句详细解释

1. 循环条件：while (child > 0)

while (child > 0)

• 作用：控制调整的终止时机，决定 "是否还要继续向上比较"。
• 逻辑推导 ：
  • 数组下标从 0 开始，child=0 代表当前节点是根节点（完全二叉树的顶层，没有父节点）。
  • 若 child > 0，说明当前节点还有父节点，需要继续向上比较；若 child=0，没有父节点可比，调整终止。
• 反例 ：如果写成 child >= 0，会导致根节点还去计算父节点（(0-1)/2 = -0.5 → 整数除法后为-0，但数组没有负下标，会越界）。

2. 计算父节点下标：int parent = (child - 1) / 2

int parent = (child - 1) / 2;

• 作用：根据当前子节点的位置，找到它的父节点在数组中的位置（这是向上调整的 "导航核心"）。
• 为什么是这个公式？ 完全二叉树中，父节点 parent 的左子节点是 2*parent + 1，右子节点是 2*parent + 2。反过来推导：
  • 若子节点是左孩子（child = 2*parent + 1）→ 父节点 parent = (child - 1)/2；
  • 若子节点是右孩子（child = 2*parent + 2）→ 父节点 parent = (child - 2)/2？错！实际用 (child - 1)/2 也能得到正确结果：例：右子节点 child=4 → (4-1)/2=1.5 → 整数除法后为1（和左子节点 child=3 的父节点一致）。结论：(child - 1)/2 是 "通式"，无论左 / 右子节点，都能正确找到父节点。

3. 小堆特性判断：if (arr[parent] > arr[child])

if (arr[parent] > arr[child])

• 作用：检查当前父子节点是否违反小堆特性，决定 "是否需要交换"。
• 逻辑推导 ：
  • 小堆要求 "父 ≤ 子"，若 arr[parent] > arr[child]，说明当前父子节点违反了小堆特性（父太大，子太小），必须交换才能修复。
  • 若 arr[parent] ≤ arr[child]，说明当前父子节点符合小堆特性，且上层所有节点（更往上的祖先）原本就是符合的（因为插入前堆是合法的），所以直接退出循环。

4. 交换父子节点的值：swapdata(&arr[parent], &arr[child])

swapdata(&arr[parent], &arr[child]);

• 作用：修复当前违反小堆特性的父子节点（把 "大的父节点" 和 "小的子节点" 交换，让父节点变小，子节点变大）。
• 为什么要传地址（&arr[parent]）？ C 语言中函数参数是 "值传递"，若直接传 arr[parent]（值），函数内部交换的是副本，原数组不会变。传地址才能真正修改原数组中父子节点的值。
• 交换后的效果：当前父子节点满足 "父 ≤ 子"，但交换后的子节点（原父节点）可能和它的父节点（原祖父节点）又违反特性，所以需要继续向上调整。

5. 更新子节点位置：child = parent

child = parent;

• 作用：让 "被交换后的子节点" 成为新的 "待检查子节点"，继续向上比较。
• 逻辑类比 ：假设原子节点是 "儿子"，父节点是 "爸爸"。交换后，"儿子" 跑到了 "爸爸" 的位置，接下来需要检查这个 "新爸爸" 是否比它的 "爷爷"（原父节点的父节点）大 ------ 所以要把 child 更新为原父节点的下标（parent），下一轮循环就会检查 "新爸爸" 和 "爷爷" 的关系。
• 反例 ：如果不更新 child，下一轮循环还是检查原来的 child（已经交换到父节点位置的旧值），会导致调整中断，堆特性无法完全修复。

6. （可选）更新父节点位置：parent = (child - 1) / 2

parent = (child - 1) / 2;

• 作用 ：提前计算下一轮循环的父节点下标（但其实这行代码可以省略）。
• 为什么可选？ 因为下一轮循环会重新执行 int parent = (child - 1) / 2，会根据更新后的 child 计算新的父节点。这行代码只是提前算了一次，不影响最终结果（属于 "冗余但无害" 的代码）。

7. 终止调整：else { break; }

else//当子节点和其父节点数据大小满足小堆的要求时，我们就直接退出循环
{
    break;
}

• 作用：当当前父子节点符合小堆特性时，直接终止循环，避免无效的后续操作。
• 关键逻辑：插入新元素前，堆本身是合法的（所有节点都满足小堆特性）。新元素只可能影响 "自己→父→祖父→...→根" 这条路径上的节点，其他路径不受影响。若当前父子节点符合 "父 ≤ 子"，则这条路径上更上层的节点（祖父、曾祖父等）必然也符合（因为原堆是合法的），所以无需继续向上，直接退出即可。

三、完整执行流程示例（结合代码走一遍）

假设现有小堆数组 [3, 5, 8, 7, 6]（符合小堆特性），现在插入新元素 2，插入后数组为 [3, 5, 8, 7, 6, 2]，新元素在 child=5 位置。

第一轮循环（child=5）

1. 循环条件：5 > 0 → 成立。
2. 计算父节点：parent=(5-1)/2=2（数组中 arr[2]=8）。
3. 比较：arr[2]=8 > arr[5]=2 → 违反小堆特性，进入 if。
4. 交换：arr[2] 和 arr[5] 交换，数组变为 [3, 5, 2, 7, 6, 8]。
5. 更新 child：child=2（现在检查位置 2 的节点）。
6. （可选）更新 parent：parent=(2-1)/2=0。

第二轮循环（child=2）

1. 循环条件：2 > 0 → 成立。
2. 计算父节点：parent=(2-1)/2=0（数组中 arr[0]=3）。
3. 比较：arr[0]=3 > arr[2]=2 → 违反小堆特性，进入 if。
4. 交换：arr[0] 和 arr[2] 交换，数组变为 [2, 5, 3, 7, 6, 8]。
5. 更新 child：child=0（现在检查位置 0 的节点）。
6. （可选）更新 parent：parent=(0-1)/2=-0（无意义，下轮循环会终止）。

第三轮循环（child=0）

1. 循环条件：0 > 0 → 不成立，循环终止。

最终数组 [2, 5, 3, 7, 6, 8] 符合小堆特性，调整完成。

四、关键注意点

1. **为什么只调整 "新元素的祖先路径"？**插入前堆是合法的，新元素只可能破坏 "自己→父→祖父" 这条路径的特性（其他路径的父子关系没被改动），所以无需检查其他节点，效率高（时间复杂度 O (log n)）。
2. 代码中的冗余行 ：parent = (child - 1) / 2 写在 if 内部是冗余的，因为下一轮循环会重新计算 parent。但保留它不影响正确性，只是多一次计算。
3. 越界风险 ：循环条件 child > 0 是防止越界的关键 ------ 若 child=0 还继续计算 parent，会得到负下标，访问数组时会崩溃。

通过以上拆解，能明确代码中每一步的 "目的" 和 "逻辑依据"，而不是单纯记代码。核心是抓住 "小堆特性" 和 "父子下标关系" 这两个关键点，就能理解向上调整的本质是 "让新元素找到自己的正确位置，保证堆不违规"。

大家可以根据下面这个图来辅助理解：

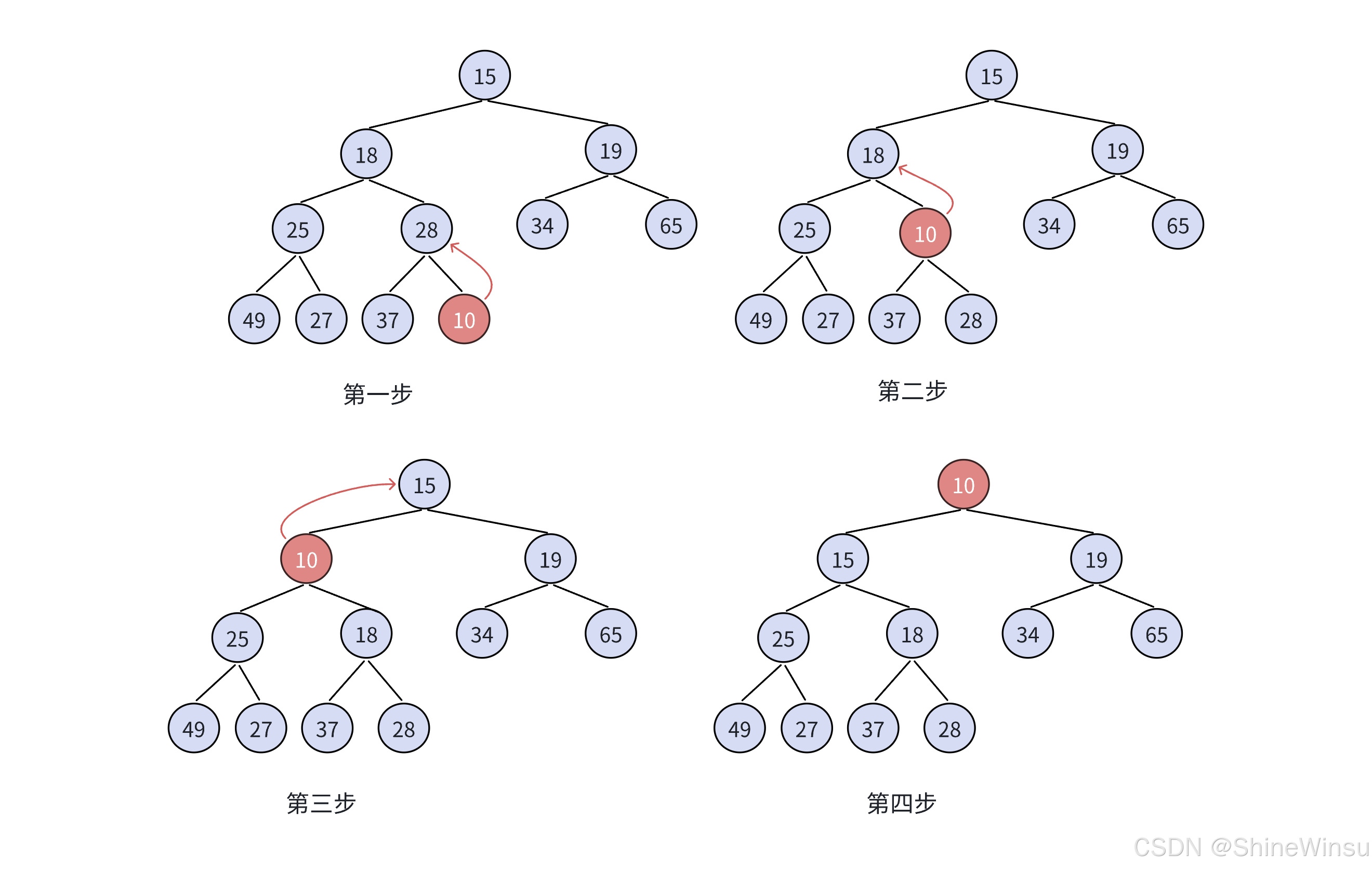
到这里，我们的向上调整算法，就解析的大差不差了，下面我就给出对堆插入数据的完整代码：

//两个数据的交换
//要用传址调用
void swapdata(name1* p1, name1* p2)
{
	name1 temp = *p1;
	*p1 = *p2;
	*p2 = temp;
}

//向上调整算法
void adjustup(name1* arr, int child)
{
	//向上调整算法：
	//先将元素插入到堆的末尾, 即最后一个孩子之后
	//插入之后如果堆的性质遭到破坏，将新插入结点顺着其双双亲往上调整到合适位置即可

	//我们肯定要借助循环去不断将最后插入的子节点
	//去与它的祖先一一比较
	//而且由于我们是实现小堆
	//所以就要求父节点的数据要小于子节点的数据大小
	//所以我们就要比较
	//一旦子节点小于父节点
	//就要把这两个节点给交换
	//这边注意，我们不仅要将这两个节点数据进行交换
	//我们还要把parent和child进行交换，看到下面的代码就能理解
	//就相当于是儿子和父亲互换了
	//原本的儿子成了爸爸，而原来的爸爸成了儿子

	//那么我们的循环条件是什么呢？
	//其实就是当我们的child大于0的时候，就进行循环
	//而一旦child到了0，我们知道，0其实就代表是根节点
	//是所有节点的祖先
	//那么child都干到了祖先，还能和什么父节点进行比较呢？

	while (child > 0)
	{
		//先通过数学关系找到子节点的父节点
		int parent = (child - 1) / 2;
		
		//比较子节点和父节点的数据大小
		//因为是小堆，所以就要求父节点数据小于子节点的数据
		
		//所以当我们发现子节点数据大小小于父节点数据
		//我们就得对调身份
		if (arr[parent] > arr[child])
		{
			//将子节点和父节点的数据进行交换
			swapdata(&arr[parent], &arr[child]);

			//child和parent二者本身也得交换
			//毕竟是原本的儿子成了爸爸，而原来的爸爸成了儿子
			child = parent;

			//接下来就得去和最开始的子节点的下一个祖先进行比较
			//所以这也是我们什么为什么要让child = parent
			//就是为了能不断找到子节点的祖先
			parent = (child - 1) / 2;
		}
		else//当子节点和其父节点数据大小满足小堆的要求时，我们就直接退出循环
		{
			break;
		}
	}
}


//对堆的插入数据
void hpinsert(hp* php, name1 x)
{
	assert(php);

	//其实就是我们直接把数据插进数组（堆）的最后
	//换句话来说就是对数组的尾插
	//但是呢，在尾插之后
	//我们是需要通过向上调整算法去将堆的数据结构安排好
	//比如小堆就是要满足父节点小于等于子节点

	//老样子，先判断数组剩余空间够不够
	if (php->size == php->capacity)
	{
		int newcapacity = php->capacity == 0 ? 2 : 2 * php->capacity;
		name1* temp = (name1*)realloc(php->arr, sizeof(name1) * newcapacity);
		if (temp == NULL)
		{
			perror("malloc false:");
			exit(1);
		}
		//记得有借有还
		php->arr = temp;
		php->capacity = newcapacity;
	}
	//进行尾插：
	php->arr[php->size] = x;
	php->size++;

	//进行向上调整算法

	//针对向上调整算法的两个参数
	//第一个参数自然就得得是我们的堆的数组
	//而第二个参数，由于我们是尾插，那么就代表其实前面的数据的顺序都是OK的
	//就这最后一个插入的数据需要与前面的父节点（祖先）进行比较
	//并根据是小堆还是大堆来进行数据的交换

	//这边也需要知道，我们的数组的最后一个有效数据
	//在数组中所对应的下标是php->size - 1
	//因为我们知道，数组是从0开始存储的
	adjustup(php->arr, php->size - 1);
}

对堆（堆顶）（根节点）的删除数据：

各位，解决了对堆的插入数据之后，怎么能少了对堆的删除数据呢？OiOi，那么对堆删除数据，我们又要怎么实现呢？

其实和对堆插入数据差不多，我们依旧是利用数组的高效性，毕竟我们要知道，数组除了尾插方便，尾删那也是嘎嘎滴方便哇。

那么问题来了，我们是要对堆顶，也就是根节点删除数据，而堆顶的数据是存储在数组的下标为0的地方的，而我们尾删又只能删除数组的最后面，那还怎么把这二者联系起来呢？

难道我们要用头删？nonono，这个绝对不可能，大家不要想，至于原因是什么？我不多说，大家没必要知道，只需要知道很麻烦就对了，没意义，相对于尾删来说，头删差劲极了。

那么我们前面说到，我们既要对栈顶数据进行删除，又要利用数组的尾删，那么，有什么办法，能够将这二者串联起来呢？其实很简单，我们将数组的最后一个数据和数组的第一个数据进行交换不就行了，这么一来堆顶的数据不就变成了数组的最后一个数据，那么这个时候，不就可以进行尾删了？perfect。

就像下图：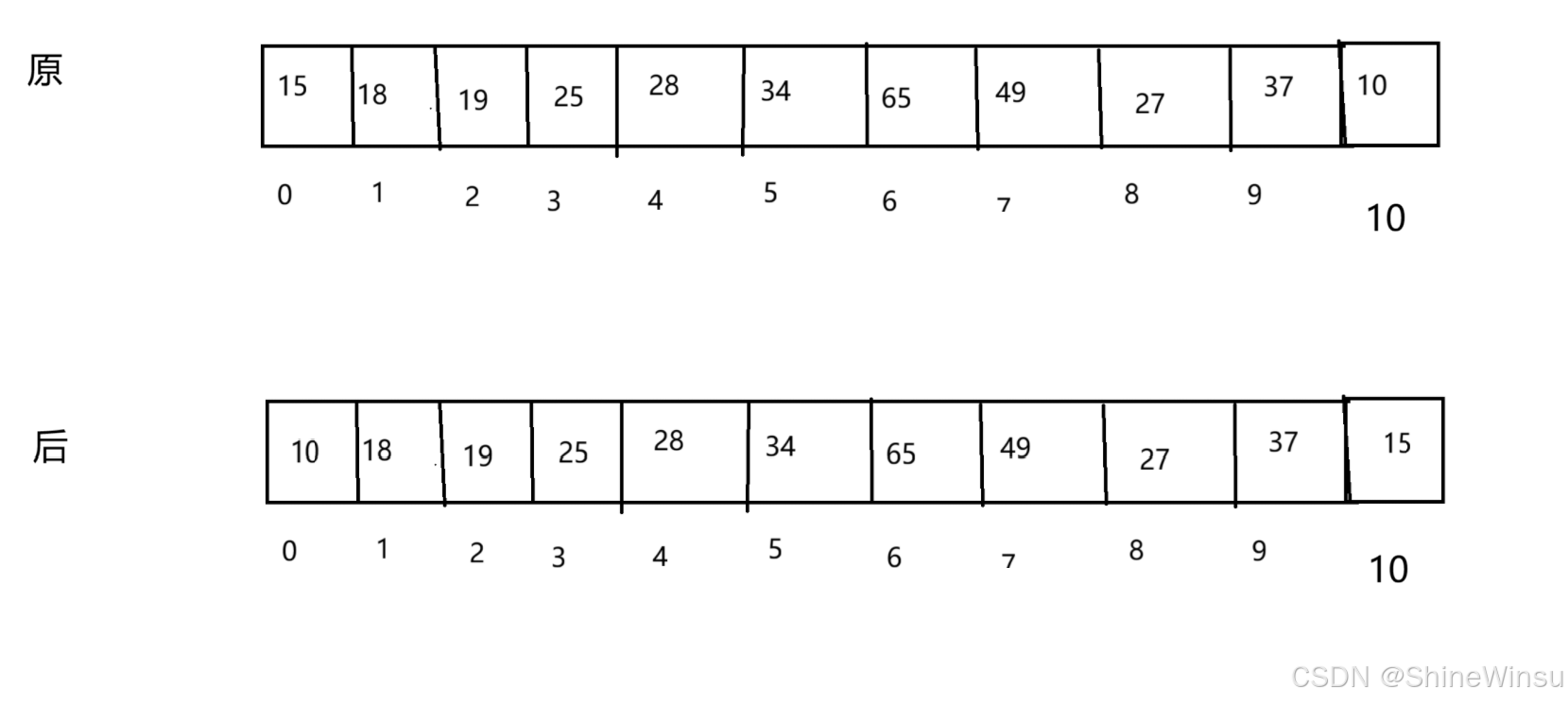

大家应该能够理解，下面是一个新例子：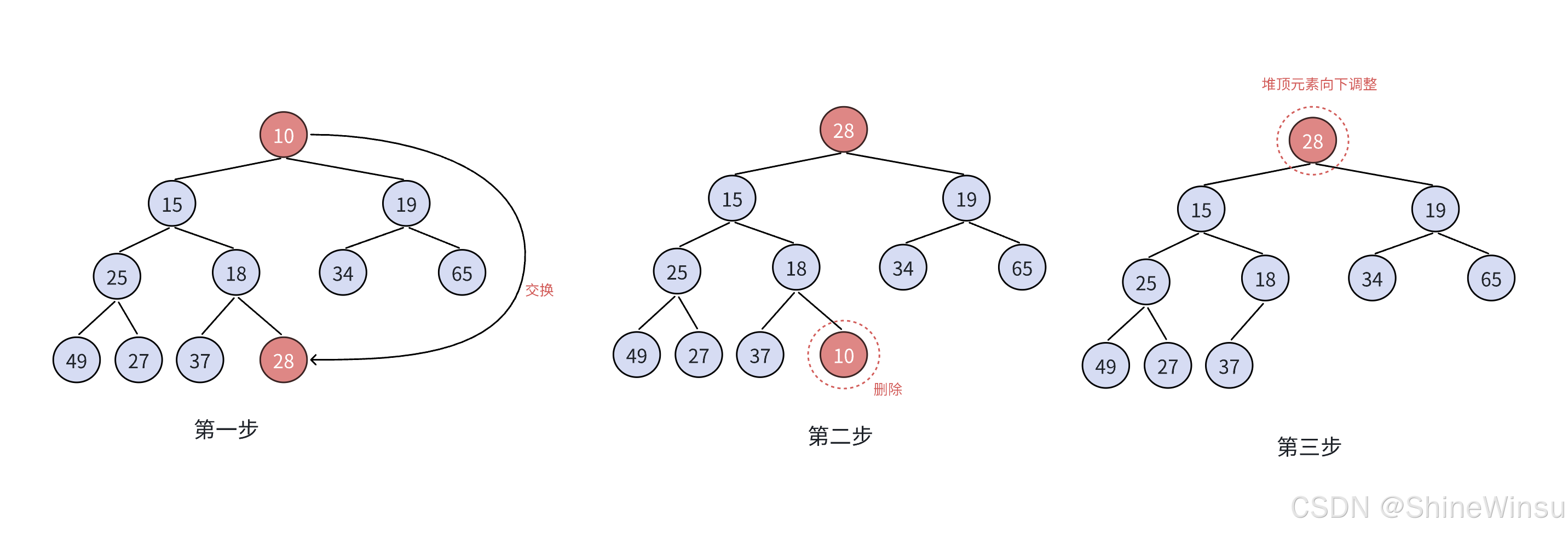

当我们将头尾数据交换之后，我们就可以进行尾删，那么对于顺序表的尾删，大家肯定不陌生，我这里就直接给出完整代码：

//对堆的删除数据
void hppop(hp* php)
{
	assert(php);
	//判断堆是否为空
	//为空删个蛋蛋
	assert(hpempty(php));

	//删除堆是删除堆顶的数据，将堆顶的数据跟最后一个数据一换，
	//然后删除数组最后一个数据，再进行向下调整算法

	//所以，我们首先要将堆（数组）的第一个数据和最后一个数据进行交换
	swapdata(&(php->arr[0]), &(php->arr[php->size - 1]));

	//接着通过数组尾删去把数组的最后一个数据给删除掉
	php->size--;

	//最后就要通过向下调整算法去将堆（数组）的顺序安排好
	//比如小堆就是要满足父节点小于等于子节点

	adjustdown(php->arr, php->size,0);
}

那么接下来就肯定又有问题了，在进行了首尾交换数据以及尾删之后，我们用头发想都知道，这之后形成的新堆，肯定是不符小堆的要求的，那么这个时候，毋庸置疑，我们又要通过算法去将这个新堆给调整好，那么是什么算法呢？

既然我们让原本的倒数第一个当了第一个，是不是就相当于是把下面的较大的数据给放到应该是最小的数据所在的地方上了（因为小堆要求父节点<=子节点，那么根节点肯定就是数据最小的地方），那么我们肯定就要从上开始，往下进行安排了，所以，这个算法就叫------向下调整算法，也就是上面代码的adjustdow函数。

向下调整算法：

向下调整算法有一个前提：左右子树必须是一个堆，才能调整。

💡 向下调整算法

• 将堆顶元素与堆中最后一个元素进行交换
• 删除堆中最后一个元素
• 将堆顶元素向下调整到满足堆特性为止

大家看下面这段话：细细理解一番

//毋庸置疑，我们肯定也要用到循环
//那么在向上调整算法中，我们循环的条件是什么呢？
//这就和我们传入的堆数组的数据个数有关了
//因为我们知道，是向下不断调整，那么就代表着是和向上调整算法反着来了
//要让原本的儿子变成爸爸，原本的爸爸变成儿子（注意，是往下的移动）
//那么在向上调整算法中，我们是循环到了孩子干到了根节点后，就停止
//那么我们向下，就让孩子干到最后没有孩子了不就行了
//意思就是说，当我们的child移动到了最后一个数据时
//就停止循环，因为此时它是没有孩子的
//那么循环条件就是，当child小于数据个数的时候进行循环
//因为我们知道，数组的最后一个有效数据的下标是size-1

与向上调整算法不同，向上调整算法是比较祖先，而向下调整算法是比较孩子，那么循环自然也就是到了某个节点没有孩子了结束。

下面是向下调整法的详细代码：

int child = parent * 2 + 1;

while (child < size)
{	
	//我们要先找到父节点所对应的子节点
    //这里注意，我们是要找父节点中较小的那一个子节点
    //因为我们知道，堆的本质是完全二叉树
    //所以，基本每个父节点都有两个孩子
    //那么我们要对父节点和子节点进行数据大小的比较
    //那我们就肯定得去找到更小的那一个子节点（因为是小堆，大堆的话就是去找更大的那一个子节点）

    //那么我们又怎么知道两个孩子中是哪个孩子的数据更小呢？
    //诶，可以使用假设法
    //我们先假设是左孩子较小
    //即如上所说的
	//int child = parent * 2 + 1;
	//接着我们去判断
	//如果右孩子的数据小于左孩子的数据
	//我们就让上面的child去+1，也就是从左孩子变为右孩子
	//对于这个if条件，我们还得注意，因为我们上面的循环条件是设置
	//child<size
	//但是我们可以看到下面有child+1的出现
	//那么这么一来，就有可能出现，child<size,但是child+1>=size的情况
	//所以，我们应该再加一个条件判断
	if (child + 1 < size && arr[child] > arr[child + 1])
	{
		child = child + 1;
	}

	//接下来我们就可以开始进行比较了
	//因为是小堆，所以当我们的子节点的数据小于我们的父节点的话
	//我们就得染让它们两个进行交换
	if (arr[child] < arr[parent])
	{
		//进行数据交换
		swapdata(&arr[child], &arr[parent]);
		
		//parent和child两个也得进行交换
		parent = child;
	
		//接着我们再次修改child，让它能进行下一个子节点进行判断
		//不用担心会不会找不到较小数据的那一个子节点
		//我们的假设法可是在循环中的
		//而也正是因为我们的假设法就在循环中
		//所以我们的child也只能先更新为左孩子
		child = parent * 2 + 1;
	}
	else//如果没有出现子节点的数据小于我们的父节点，我们就直接循环终止
	{
		break;
	}
}

下面是向下调整法的详细解释：

下面对向下调整算法（小堆）进行极致详细的解析，从原理到代码逐行拆解，结合实例说明每一步的设计逻辑：

一、算法本质与适用场景

本质 ：当堆顶元素被移除或修改后，通过 "自上而下" 的比较交换，将异常节点（通常是新堆顶）移动到合适位置，恢复 "父节点值 ≤ 子节点值" 的小堆特性。前提 ：被调整节点的左右子树必须已是合法的堆 （这是算法能生效的核心条件）。适用场景：

1. 堆顶元素删除后（如 hppop 操作）；
2. 从数组初始化堆时（从最后一个非叶子节点向前调整）。

二、函数参数详解

函数原型：void adjustdown(name1* arr, int size, int parent)

• arr：堆的底层数组（完全二叉树的顺序存储，通过下标访问节点）。
• size：堆中有效元素的数量（用于判断子节点是否越界，避免访问无效内存）。
• parent：需要调整的起始父节点下标（删除操作中初始为 0，即堆顶）。

三、代码逐行深度解析

1. 初始化子节点：int child = parent * 2 + 1

int child = parent * 2 + 1;

• 作用 ：计算当前父节点的左子节点下标，这是向下调整的起点。
• 数学依据 ：完全二叉树中，父节点 parent 的左子节点固定为 2*parent + 1，右子节点为 2*parent + 2。
• 设计逻辑：采用 "假设法"，先默认左子节点是两个子节点中较小的那个（小堆需要与更小的子节点比较），后续通过比较修正。

2. 循环条件：while (child < size)

while (child < size)

• 作用：控制调整的终止时机，确保只在有效节点范围内操作。
• 逻辑推导 ：
  • 数组下标范围是 [0, size-1]，若 child < size：子节点存在（下标合法），需要继续调整。
  • 若 child >= size：子节点不存在（当前父节点是叶子节点，无子女），调整终止。
• 与向上调整的区别 ：向上调整终止于 "无父节点"（child > 0），向下调整终止于 "无子女节点"（child < size），方向完全相反。

3. 选择更小的子节点：if (child + 1 < size && arr[child] > arr[child + 1])

if (child + 1 < size && arr[child] > arr[child + 1])
{
    child = child + 1;
}

• 作用：在左右子节点中，找到值更小的那个子节点（小堆要求父节点与更小的子节点比较交换）。
• 条件拆解 ：
  • child + 1 < size：确保右子节点存在（避免访问 arr[child+1] 时越界）。
  • arr[child] > arr[child + 1]：若右子节点值 < 左子节点值，则更新 child 为右子节点下标。
• 反例 ：若省略 child + 1 < size，当父节点只有左子节点时（如最后一个非叶子节点），child+1 可能等于 size，导致访问越界。

4. 比较父子节点：if (arr[child] < arr[parent])

if (arr[child] < arr[parent])

• 作用：检查当前父子节点是否违反小堆特性，决定是否需要交换。
• 小堆特性 ：父节点值必须 ≤ 子节点值。若 arr[child] < arr[parent]，说明父节点值过大，违反特性，需要交换；否则无需调整。

5. 交换父子节点的值：swapdata(&arr[child], &arr[parent])

swapdata(&arr[child], &arr[parent]);

• 作用：通过交换修复当前层级的小堆特性（父节点值变小，子节点值变大）。
• 为什么传地址：C 语言是值传递，只有传指针（地址）才能真正修改原数组中的值。
• 交换后的影响：原父节点的值被移到子节点位置，可能破坏该子节点与其后代的堆特性，因此需要继续向下调整。

6. 更新父节点位置：parent = child

parent = child;

• 作用：将父节点的位置 "下移" 到被交换的子节点位置，准备检查下一层的父子关系。
• 类比：原父节点 "降级" 为子节点后，需要以它为新的父节点，继续检查它与它的子节点是否符合堆特性。

7. 更新子节点位置：child = parent * 2 + 1

child = parent * 2 + 1;

• 作用：计算新父节点的左子节点下标，为下一轮循环做准备（继续向下比较）。
• 设计逻辑：无论上一轮是左子还是右子节点，新一轮都先默认左子节点为较小值（后续会通过步骤 3 修正）。

8. 终止调整：else { break; }

else//如果没有出现子节点的数据小于我们的父节点，我们就直接循环终止
{
    break;
}

• 作用：当当前父子节点满足小堆特性时，立即终止循环，避免无效操作。
• 深层逻辑：由于左右子树原本就是合法的堆，若当前父节点无需交换，则其所有后代节点也必然满足堆特性（无需继续向下检查）。

四、完整执行实例（可视化过程）

假设小堆数组为 [2, 5, 3, 7, 6, 8]（size=6），删除堆顶元素 2 后：

1. 交换堆顶与末尾元素：数组变为 [8, 5, 3, 7, 6]（size=5），需对新堆顶 parent=0（值 8）执行向下调整。

第一轮循环（parent=0）

• 初始化子节点：child = 0*2 + 1 = 1（左子节点，值 5）。
• 循环条件：1 < 5 → 成立。
• 检查右子节点：child+1=2 < 5 且 arr[1]=5 > arr[2]=3 → 更新 child=2（右子节点，值 3）。
• 比较父子：arr[2]=3 < arr[0]=8 → 违反特性，交换后数组变为 [3, 5, 8, 7, 6]。
• 更新父节点：parent=2（原子节点位置）。
• 更新子节点：child=2*2 + 1 = 5（新父节点的左子节点）。

第二轮循环（parent=2）

• 循环条件：5 < 5 → 不成立（child=5 等于 size=5，子节点不存在）。
• 循环终止，调整完成。

最终数组 [3, 5, 8, 7, 6] 符合小堆特性：

        3（0）
      /   \
    5（1）  8（2）
   /  \
7（3） 6（4）

五、关键细节与注意事项

1. **为什么必须 "左右子树已是堆"？**若子树不是堆，即使当前父子节点交换，也无法保证整体堆特性。例如：若右子树本身违反小堆特性，仅调整当前父节点无法修复。
2. 时间复杂度为何是 O (log n)？ 最多调整次数等于树的高度，对于 n 个节点的完全二叉树，高度为 log₂n（向上取整），因此时间复杂度为对数级。
3. 如何改为大堆？ 只需修改两个比较条件：
   • 选择子节点时：arr[child] < arr[child + 1]（找更大的子节点）。
   • 父子比较时：arr[child] > arr[parent]（子节点更大则交换）。

通过上述解析可见，向下调整算法的每一步都围绕 "修复堆特性" 设计，利用完全二叉树的数学关系精准定位节点，以最小的比较交换次数完成调整，是堆操作中不可或缺的核心算法。

大家可以看下面这幅图进行理解：

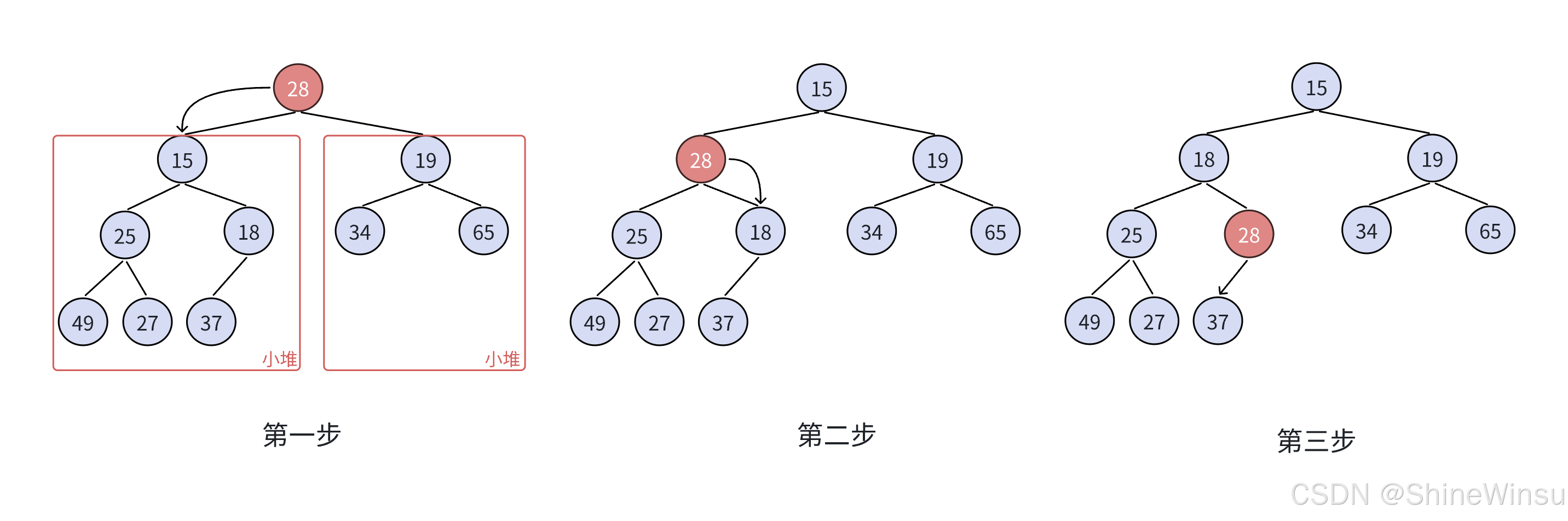
到这里，我们的向下调整算法，就解析的大差不差了，下面我就给出对堆删除数据的完整代码：

//两个数据的交换
//要用传址调用
void swapdata(name1* p1, name1* p2)
{
	name1 temp = *p1;
	*p1 = *p2;
	*p2 = temp;
}


//向下调整算法
void adjustdown(name1* arr, int size, int parent)
{
	//向下调整算法有一个前提：左右子树必须是一个堆，才能调整。
	//💡 向下调整算法
	//• 将堆顶元素向下调整到满足堆特性为止

	//毋庸置疑，我们肯定也要用到循环
	//那么在向上调整算法中，我们循环的条件是什么呢？
	//这就和我们传入的堆数组的数据个数有关了
	//因为我们知道，是向下不断调整，那么就代表着是和向上调整算法反着来了
	//要让原本的儿子变成爸爸，原本的爸爸变成儿子（注意，是往下的移动）
	//那么在向上调整算法中，我们是循环到了孩子干到了根节点后，就停止
	//那么我们向下，就让孩子干到最后没有孩子了不就行了
	//意思就是说，当我们的child移动到了最后一个数据时
	//就停止循环，因为此时它是没有孩子的
	//那么循环条件就是，当child小于数据个数的时候进行循环
	//因为我们知道，数组的最后一个有效数据的下标是size-1
	
	int child = parent * 2 + 1;

	while (child < size)
	{	
		//我们要先找到父节点所对应的子节点
	    //这里注意，我们是要找父节点中较小的那一个子节点
	    //因为我们知道，堆的本质是完全二叉树
	    //所以，基本每个父节点都有两个孩子
	    //那么我们要对父节点和子节点进行数据大小的比较
	    //那我们就肯定得去找到更小的那一个子节点（因为是小堆，大堆的话就是去找更大的那一个子节点）

	    //那么我们又怎么知道两个孩子中是哪个孩子的数据更小呢？
	    //诶，可以使用假设法
	    //我们先假设是左孩子较小
	    //即如上所说的
		//int child = parent * 2 + 1;
		//接着我们去判断
		//如果右孩子的数据小于左孩子的数据
		//我们就让上面的child去+1，也就是从左孩子变为右孩子
		//对于这个if条件，我们还得注意，因为我们上面的循环条件是设置
		//child<size
		//但是我们可以看到下面有child+1的出现
		//那么这么一来，就有可能出现，child<size,但是child+1>=size的情况
		//所以，我们应该再加一个条件判断
		if (child + 1 < size && arr[child] > arr[child + 1])
		{
			child = child + 1;
		}

		//接下来我们就可以开始进行比较了
		//因为是小堆，所以当我们的子节点的数据小于我们的父节点的话
		//我们就得染让它们两个进行交换
		if (arr[child] < arr[parent])
		{
			//进行数据交换
			swapdata(&arr[child], &arr[parent]);
			
			//parent和child两个也得进行交换
			parent = child;
		
			//接着我们再次修改child，让它能进行下一个子节点进行判断
			//不用担心会不会找不到较小数据的那一个子节点
			//我们的假设法可是在循环中的
			//而也正是因为我们的假设法就在循环中
			//所以我们的child也只能先更新为左孩子
			child = parent * 2 + 1;
		}
		else//如果没有出现子节点的数据小于我们的父节点，我们就直接循环终止
		{
			break;
		}
	}

}



//对堆的删除数据
void hppop(hp* php)
{
	assert(php);
	//判断堆是否为空
	//为空删个蛋蛋
	assert(hpempty(php));

	//删除堆是删除堆顶的数据，将堆顶的数据跟最后一个数据一换，
	//然后删除数组最后一个数据，再进行向下调整算法

	//所以，我们首先要将堆（数组）的第一个数据和最后一个数据进行交换
	swapdata(&(php->arr[0]), &(php->arr[php->size - 1]));

	//接着通过数组尾删去把数组的最后一个数据给删除掉
	php->size--;

	//最后就要通过向下调整算法去将堆（数组）的顺序安排好
	//比如小堆就是要满足父节点小于等于子节点

	//那么对于向下调整算法的三个参数，我们依旧需要知道
	//第一个参数和向上调整算法一样，要传入我们的堆数组
	//而第二个参数，则是要传入我们堆数组的数据个数
	//这个参数是用于我们在向下调整算法中的循环条件
	//那么第三个参数，其实就是父节点（祖先）的下标
	////又因为是向下调整算法，所以我们自然要从二叉树的根节点开始
	//我们的堆的根节点的所对应的下标又是0
	//所以，我们一开始就是传0进去
	//后续在函数中，我们再不断更新父节点
	adjustdown(php->arr, php->size,0);
}

对于向下调整算法和向上调整算法循环条件的一个总结：

OK大家，当我写这一段话的时候，是已经离我写完这篇博客有一个多月的时间了，哈哈，主要是我也没想到，当我时隔一个多月去再写向下调整算法和向上调整算法的时候，竟然发现自己对循环条件有些不太清晰明了，那么其实这是很可怕的，毕竟向下调整算法和向上调整算法都是由循环撑起来的，所以呢，我必须去再加一些关于这个循环条件的解释：

那么我们可以关注到，其实向下调整算法和向上调整算法的循环条件都是和child，子节点有关，额，这是为什么呢，其实是有原因的，我们先看向上调整算法，

while (child > 0)//当孩子滚到根节点去了，那它哪里还有父母呢，所以也就无意义了
{
	//因为下面会有parent = (child - 1) / 2;，所以child不能到0，不难就会越界
	if (con[parent] < con[child])//创建大堆
	{
		std::swap(con[parent], con[child]);
		child = parent;
		parent = (child - 1) / 2;
	}  
    ......
}

可以发现，是child>0的时候才能继续进行循环，那么这是为什么呢？其实这是为了不越界，我们必须要明确一点，循环条件的设置，就是为了不让下面的循环体内出现越界的情况，尤其是对于数组而言，那么对于向上调整算法，我们可以看到，下面是有parent = (child - 1) / 2;的，那么这个就很危险了，为什么呢，因为如果当child移动到最上面的根节点的时候，那是不是就意味着parent就跑到负数去了，那么这个时候我们不做限制的话，时不时就会出现con[parent]越界的情况了，那么这个时候有人可能会说，那为什么不设置parent>0为循环条件呢？那这样子的话，当parent为0的时候，其实是child为1或者2，也就是最上面根节点的下面两个孩子，那么这个时候我们直接退出循环了，那么最上面的根节点和它的孩子不就没有进行比较了吗，那么这个时候就会有问题了，所以我们是不能设置parent>0为循环条件，而设置child>0为限制条件是完全没问题的，毕竟当child移动到最上面的根节点的时候，不就代表都所有父节点和子节点都比较完了吗，所以其实大家还是要依靠例子去进行理解，或者也可以强行记忆，孩子是最调皮的，所以我们得严格控制孩子。

我们再看向下调整算法：

while (child < con.size())
{
	//因为下面有child = parent * 2 + 1;，那么如果计算，child越界了，那就肯定不能再循环了
	//而如果是parent< con.size()，那么其实很有可能会孩子越界而不自知
	//而要是child < con.size()，我们能确保child和parent都不越界
	if (child + 1 < con.size() && con[child] < con[child + 1])
	{
		child = child + 1;//如果是右孩子比较大的话，就把child替换为右孩子
	}
	if (con[parent] < con[child])
	{
		std::swap(con[parent], con[child]);
		parent = child;
		child = parent * 2 + 1;
	}
	else
	{
		break;//同样的，没达到条件那不是直接滚蛋吗		
    }
}

我们可以看到，是把循环条件设置为child<堆中的数据个数，即数组中最后一个有效数据的下标，那么这个又是为什么呢？其实是因为下面有个child = parent * 2 + 1;，那么大家看这个，这个是不是有非常大的越界的风险呢？如果我们没有对child进行管控的话，那么child跑到多后面去都不知道，说白了其实还是为了避免越界，要是我们是设置parent为循环条件的话，那么大家，当parent到了数组倒二个数据或者倒一个数据的时候，想想，child跑到哪里去了，早就跑飞了，那么这个时候我们是还没退出循环的，那么child是不是就越界了，就是这么个道理，大家一定要结合例子好好思考极端情况。

OK划重点，最关键最核心的总结来了家人们，三十年经验，三十秒教给大家，我们只需要记住一点，孩子是最调皮的，我们为了它的安全，我们必须管控他，既不能让它跑到最后一个数据去，也不能让它跑到第一个数据去，不难孩子就有可能会起飞了，哈哈哈哈哈 ，希望大家牢记。

对堆顶元素的取用以及删除：

这个其实就很简单了，这个主要是和我们下篇博客要讲的堆排序有关。

那么我们要如何取用堆顶元素呢？其实很简单，我们直接设置一个变量保存堆顶元素，然后再删除堆顶元素，最后把那个变量传回即可，是不是很简单，我们只接看详细代码：

//对堆顶的数据的取用以及删除
name1 hptop(hp* php)
{
	assert(php);
	//判断堆是否为空
	//为空删个蛋蛋
	assert(hpempty(php));

	if (hpempty(php))
	{
		return -1;
	}
	//其实这个很简单
	//我们先设置变量去保存堆顶的数据
	//其实也就是数组的第一个数据
	name1 ret = php->arr[0];
	//调用删除函数
	hppop(php);

	return ret;
}

OK诸位，到这里，我们的堆的实现，也就差不多了，下面我就给出实现堆的头文件，源文件以及测试源文件：

堆的头文件：

#pragma once
#include<stdio.h>
#include<assert.h>
#include<ctype.h>
#include<errno.h>
#include<float.h>
#include<iso646.h>
#include<limits.h>
#include<locale.h>
#include<math.h>
#include<stdarg.h>
#include<stddef.h>
#include<stdlib.h>
#include<string.h>
#include<time.h>
#include<complex.h>
#include<stdbool.h>
#include<tgmath.h>
#include<signal.h>
#include<setjmp.h>
#include<inttypes.h>

//堆底层结构为数组，因此定义堆的结构为
//因为堆是用来表示完全二叉树
//所以，我们是用顺序表，也就是数组结构去实现堆
//换句话来说就是，我们要把完全二叉树中的
//每一个节点（有对应的序号）存储进数组的对应的小标的格子中
//所以，我们依旧是需要定义一个顺序表，也就是数组结构
//和之前所学的顺序表结构类似

typedef int name1;

struct heap
{
	name1* arr;
	int size;
	int capacity;
};

typedef struct heap hp;

//对堆的初始化
void hpinit(hp* php);

//对堆的销毁
void hpbreak(hp* php);

//利用给定数组初始化堆
void hpinitfromarr(hp* php, name1* inputarr,int n);

//对堆的插入数据
void hpinsert(hp* php, name1 x);

//对堆的删除数据
void hppop(hp* php);

//对堆顶的数据的取用以及删除
name1 hptop(hp* php);

//判断堆是否为空
bool hpempty(hp* php);

//求堆中数据的个数
int hpsize(hp* php);

//向上调整算法
//针对向上调整算法的两个参数
//第一个参数自然就得得是我们的堆的数组
//而第二个参数，由于我们是尾插，那么就代表其实前面的数据的顺序都是OK的
//就这最后一个插入的数据需要与前面的父节点（祖先）进行比较
//并根据是小堆还是大堆来进行数据的交换
//而之所以我们要把第二个参数命名为child
//是因为最后插入的数据
//肯定是子节点，毕竟我们又不是直接插个父节点进去
void adjustup(name1* a,int child);

//向下调整算法
//那么对于向下调整算法的三个参数，我们依旧需要知道
//第一个参数和向上调整算法一样，要传入我们的堆数组
//而第二个参数，则是要传入我们堆数组的数据个数
//这个参数是用于我们在向下调整算法中的循环条件
//那么第三个参数，其实就是父节点（祖先）的下标
//又因为是向下调整算法，所以我们自然要从二叉树的根节点开始
//我们的堆的根节点的所对应的下标又是0
//所以，我们一开始就是传0进去
//后续在函数中，我们再不断更新父节点
void adjustdown(name1* a,int size,int parent);

//两个数据的交换
//要用传址调用
void swapdata(name1* p1,name1* p2);

堆的源文件：

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<assert.h>
#include<ctype.h>
#include<errno.h>
#include<float.h>
#include<iso646.h>
#include<limits.h>
#include<locale.h>
#include<math.h>
#include<stdarg.h>
#include<stddef.h>
#include<stdlib.h>
#include<string.h>
#include<time.h>
#include<complex.h>
#include<stdbool.h>
#include<tgmath.h>
#include<signal.h>
#include<setjmp.h>
#include<inttypes.h>

#include"smallheap.h"

//对堆的初始化
void hpinit(hp* php)
{
	assert(php);
	php->arr = NULL;
	php->size = 0;
	php->capacity = 0;
}

//对堆的销毁
void hpbreak(hp* php)
{
	assert(php);
	free(php->arr);
	php->arr = NULL;
	php->size = 0;
	php->capacity = 0;
}

//两个数据的交换
//要用传址调用
void swapdata(name1* p1, name1* p2)
{
	name1 temp = *p1;
	*p1 = *p2;
	*p2 = temp;
}

//求堆中数据的个数
int hpsize(hp* php)
{
	assert(php);
	//和顺序表差不多，我们直接返回size就行
	return php->size;
}

//向上调整算法
void adjustup(name1* arr, int child)
{
	//向上调整算法：
	//先将元素插入到堆的末尾, 即最后一个孩子之后
	//插入之后如果堆的性质遭到破坏，将新插入结点顺着其双双亲往上调整到合适位置即可

	//我们肯定要借助循环去不断将最后插入的子节点
	//去与它的祖先一一比较
	//而且由于我们是实现小堆
	//所以就要求父节点的数据要小于子节点的数据大小
	//所以我们就要比较
	//一旦子节点小于父节点
	//就要把这两个节点给交换
	//这边注意，我们不仅要将这两个节点数据进行交换
	//我们还要把parent和child进行交换，看到下面的代码就能理解
	//就相当于是儿子和父亲互换了
	//原本的儿子成了爸爸，而原来的爸爸成了儿子

	//那么我们的循环条件是什么呢？
	//其实就是当我们的child大于0的时候，就进行循环
	//而一旦child到了0，我们知道，0其实就代表是根节点
	//是所有节点的祖先
	//那么child都干到了祖先，还能和什么父节点进行比较呢？

	while (child > 0)
	{
		//先通过数学关系找到子节点的父节点
		int parent = (child - 1) / 2;
		
		//比较子节点和父节点的数据大小
		//因为是小堆，所以就要求父节点数据小于子节点的数据
		
		//所以当我们发现子节点数据大小小于父节点数据
		//我们就得对调身份
		if (arr[parent] > arr[child])
		{
			//将子节点和父节点的数据进行交换
			swapdata(&arr[parent], &arr[child]);

			//child和parent二者本身也得交换
			//毕竟是原本的儿子成了爸爸，而原来的爸爸成了儿子
			child = parent;

			//接下来就得去和最开始的子节点的下一个祖先进行比较
			//所以这也是我们什么为什么要让child = parent
			//就是为了能不断找到子节点的祖先
			parent = (child - 1) / 2;
		}
		else//当子节点和其父节点数据大小满足小堆的要求时，我们就直接退出循环
		{
			break;
		}
	}
}


//对堆的插入数据
void hpinsert(hp* php, name1 x)
{
	assert(php);

	//其实就是我们直接把数据插进数组（堆）的最后
	//换句话来说就是对数组的尾插
	//但是呢，在尾插之后
	//我们是需要通过向上调整算法去将堆的数据结构安排好
	//比如小堆就是要满足父节点小于等于子节点

	//老样子，先判断数组剩余空间够不够
	if (php->size == php->capacity)
	{
		int newcapacity = php->capacity == 0 ? 2 : 2 * php->capacity;
		name1* temp = (name1*)realloc(php->arr, sizeof(name1) * newcapacity);
		if (temp == NULL)
		{
			perror("malloc false:");
			exit(1);
		}
		//记得有借有还
		php->arr = temp;
		php->capacity = newcapacity;
	}
	//进行尾插：
	php->arr[php->size] = x;
	php->size++;

	//进行向上调整算法

	//针对向上调整算法的两个参数
	//第一个参数自然就得得是我们的堆的数组
	//而第二个参数，由于我们是尾插，那么就代表其实前面的数据的顺序都是OK的
	//就这最后一个插入的数据需要与前面的父节点（祖先）进行比较
	//并根据是小堆还是大堆来进行数据的交换

	//这边也需要知道，我们的数组的最后一个有效数据
	//在数组中所对应的下标是php->size - 1
	//因为我们知道，数组是从0开始存储的
	adjustup(php->arr, php->size - 1);
}

//向下调整算法
void adjustdown(name1* arr, int size, int parent)
{
	//向下调整算法有一个前提：左右子树必须是一个堆，才能调整。
	//💡 向下调整算法
	//• 将堆顶元素向下调整到满足堆特性为止

	//毋庸置疑，我们肯定也要用到循环
	//那么在向上调整算法中，我们循环的条件是什么呢？
	//这就和我们传入的堆数组的数据个数有关了
	//因为我们知道，是向下不断调整，那么就代表着是和向上调整算法反着来了
	//要让原本的儿子变成爸爸，原本的爸爸变成儿子（注意，是往下的移动）
	//那么在向上调整算法中，我们是循环到了孩子干到了根节点后，就停止
	//那么我们向下，就让孩子干到最后没有孩子了不就行了
	//意思就是说，当我们的child移动到了最后一个数据时
	//就停止循环，因为此时它是没有孩子的
	//那么循环条件就是，当child小于数据个数的时候进行循环
	//因为我们知道，数组的最后一个有效数据的下标是size-1
	
	int child = parent * 2 + 1;

	while (child < size)
	{	
		//我们要先找到父节点所对应的子节点
	    //这里注意，我们是要找父节点中较小的那一个子节点
	    //因为我们知道，堆的本质是完全二叉树
	    //所以，基本每个父节点都有两个孩子
	    //那么我们要对父节点和子节点进行数据大小的比较
	    //那我们就肯定得去找到更小的那一个子节点（因为是小堆，大堆的话就是去找更大的那一个子节点）

	    //那么我们又怎么知道两个孩子中是哪个孩子的数据更小呢？
	    //诶，可以使用假设法
	    //我们先假设是左孩子较小
	    //即如上所说的
		//int child = parent * 2 + 1;
		//接着我们去判断
		//如果右孩子的数据小于左孩子的数据
		//我们就让上面的child去+1，也就是从左孩子变为右孩子
		//对于这个if条件，我们还得注意，因为我们上面的循环条件是设置
		//child<size
		//但是我们可以看到下面有child+1的出现
		//那么这么一来，就有可能出现，child<size,但是child+1>=size的情况
		//所以，我们应该再加一个条件判断
		if (child + 1 < size && arr[child] > arr[child + 1])
		{
			child = child + 1;
		}

		//接下来我们就可以开始进行比较了
		//因为是小堆，所以当我们的子节点的数据小于我们的父节点的话
		//我们就得染让它们两个进行交换
		if (arr[child] < arr[parent])
		{
			//进行数据交换
			swapdata(&arr[child], &arr[parent]);
			
			//parent和child两个也得进行交换
			parent = child;
		
			//接着我们再次修改child，让它能进行下一个子节点进行判断
			//不用担心会不会找不到较小数据的那一个子节点
			//我们的假设法可是在循环中的
			//而也正是因为我们的假设法就在循环中
			//所以我们的child也只能先更新为左孩子
			child = parent * 2 + 1;
		}
		else//如果没有出现子节点的数据小于我们的父节点，我们就直接循环终止
		{
			break;
		}
	}

}



//对堆的删除数据
void hppop(hp* php)
{
	assert(php);
	//判断堆是否为空
	//为空删个蛋蛋
	assert(hpempty(php));

	//删除堆是删除堆顶的数据，将堆顶的数据跟最后一个数据一换，
	//然后删除数组最后一个数据，再进行向下调整算法

	//所以，我们首先要将堆（数组）的第一个数据和最后一个数据进行交换
	swapdata(&(php->arr[0]), &(php->arr[php->size - 1]));

	//接着通过数组尾删去把数组的最后一个数据给删除掉
	php->size--;

	//最后就要通过向下调整算法去将堆（数组）的顺序安排好
	//比如小堆就是要满足父节点小于等于子节点

	//那么对于向下调整算法的三个参数，我们依旧需要知道
	//第一个参数和向上调整算法一样，要传入我们的堆数组
	//而第二个参数，则是要传入我们堆数组的数据个数
	//这个参数是用于我们在向下调整算法中的循环条件
	//那么第三个参数，其实就是父节点（祖先）的下标
	////又因为是向下调整算法，所以我们自然要从二叉树的根节点开始
	//我们的堆的根节点的所对应的下标又是0
	//所以，我们一开始就是传0进去
	//后续在函数中，我们再不断更新父节点
	adjustdown(php->arr, php->size,0);
}

//对堆顶的数据的取用以及删除
name1 hptop(hp* php)
{
	assert(php);
	//判断堆是否为空
	//为空删个蛋蛋
	assert(hpempty(php));

	if (hpempty(php))
	{
		return -1;
	}
	//其实这个很简单
	//我们先设置变量去保存堆顶的数据
	//其实也就是数组的第一个数据
	name1 ret = php->arr[0];
	//调用删除函数
	hppop(php);

	return ret;
}


//判断堆是否为空
bool hpempty(hp* php)
{
	if (php->size == 0)
	{
		return true;
	}
	else
	{
		return false;
	}
}

//利用给定数组初始化堆
void hpinitfromarr(hp* php, name1* inputarr, int n)
{
	//其实就是把用户所给的数据数组丢到堆里面
	//而堆其实就是我们之前床架创建的数组
	//n是被传入数组的数据个数

	//先开辟空间
	name1* temp = (name1*)malloc(n * sizeof(name1));
	if (temp == NULL)
	{
		perror("malloc false");
		exit(1);
	}
	php->arr = temp;
	for (int i = 0; i < n; i++)
	{
		//借助循环传入我们的堆
		php->arr[php->size++] = inputarr[i];
	}

	//那么经过上面只是初步把数组的数据转移了
	//还没有达到我们堆的排列方式
	//我们要将其修改为我们正确的堆的排列方式
	//借助我们的向上调整算法即可
	for (int i = (php->size - 1 - 1) / 2; i >= 0; i--)
	{
		adjustup(php->arr, i);
	}
}

堆的测试源文件：

#include "smallheap.h"  // 包含你实现的小堆头文件

// 打印堆的当前元素（用于观察堆的结构）
void PrintHeap(hp* php) {
    assert(php);
    if (hpempty(php)) {  // 先判断堆是否为空
        printf("堆为空！\n");
        return;
    }
    printf("当前堆元素（共%d个）：", hpsize(php));
    for (int i = 0; i < php->size; i++) {
        printf("%d ", php->arr[i]);
    }
    printf("\n");
}

// 测试1：堆的初始化、插入、取堆顶、删除操作
void TestHeapBasic() {
    printf("==================== 测试1：基础操作（初始化+插入+删除+取堆顶） ====================\n");
    hp hp1;
    // 1. 初始化堆
    hpinit(&hp1);
    printf("初始化后：");
    PrintHeap(&hp1);  // 预期：堆为空

    // 2. 插入元素（随机顺序插入，验证小堆特性）
    int insertData[] = { 5, 3, 8, 2, 7, 1, 6 };
    int insertSize = sizeof(insertData) / sizeof(insertData[0]);
    for (int i = 0; i < insertSize; i++) {
        hpinsert(&hp1, insertData[i]);
        printf("插入%d后：", insertData[i]);
        PrintHeap(&hp1);  // 每次插入后，堆顶应为当前最小值
    }

    // 3. 取堆顶并删除（验证小堆排序特性：每次取到的是最小值）
    printf("\n依次取堆顶并删除：");
    int heapSize = hpsize(&hp1);
    for (int i = 0; i < heapSize; i++) {
        name1 top = hptop(&hp1);  // 取堆顶（最小值）并删除
        printf("%d ", top);       // 预期输出：1 2 3 5 6 7 8（升序）
    }
    printf("\n删除所有元素后：");
    PrintHeap(&hp1);  // 预期：堆为空

    // 4. 销毁堆（避免内存泄漏）
    hpbreak(&hp1);
    printf("===============================================================================\n\n");
}

// 测试2：通过数组初始化堆
void TestHeapInitFromArr() {
    printf("==================== 测试2：通过数组初始化堆 ====================\n");
    hp hp2;
    hpinit(&hp2);  // 先初始化空堆

    // 待初始化的数组（随机顺序）
    int initData[] = { 9, 4, 10, 1, 5, 3 };
    int initSize = sizeof(initData) / sizeof(initData[0]);
    printf("原始数组：");
    for (int i = 0; i < initSize; i++) {
        printf("%d ", initData[i]);
    }
    printf("\n");

    // 用数组初始化堆
    hpinitfromarr(&hp2, initData, initSize);
    printf("数组初始化后的堆：");
    PrintHeap(&hp2);  // 预期：堆顶为1，整体满足小堆特性（如[1,4,3,9,5,10]）

    // 验证：依次取堆顶，应得到升序序列
    printf("依次取堆顶并删除：");
    int heapSize = hpsize(&hp2);
    for (int i = 0; i < heapSize; i++) {
        name1 top = hptop(&hp2);
        printf("%d ", top);  // 预期输出：1 3 4 5 9 10
    }
    printf("\n");

    hpbreak(&hp2);  // 销毁堆
    printf("==================================================================\n\n");
}

// 测试3：边界场景（空堆、单个元素、重复元素）
void TestHeapEdgeCases() {
    printf("==================== 测试3：边界场景 ====================\n");
    hp hp3;
    hpinit(&hp3);

    // 场景1：空堆取堆顶/删除（验证断言是否生效，需注释断言观察崩溃，默认断言会阻止非法操作）
    printf("场景1：空堆操作（断言保护，不会崩溃）\n");
    // 若取消下面两行注释，运行时会触发assert报错（提示堆为空）
    // hptop(&hp3);  
    // hppop(&hp3);  

    // 场景2：单个元素的堆
    printf("场景2：单个元素堆\n");
    hpinsert(&hp3, 100);
    printf("插入100后：");
    PrintHeap(&hp3);  // 预期：[100]
    name1 top = hptop(&hp3);
    printf("取堆顶后：%d，堆状态：", top);  // 预期：100，堆为空
    PrintHeap(&hp3);

    // 场景3：重复元素的堆
    printf("场景3：重复元素堆\n");
    int repeatData[] = { 5, 3, 5, 2, 3, 2 };
    int repeatSize = sizeof(repeatData) / sizeof(repeatData[0]);
    for (int i = 0; i < repeatSize; i++) {
        hpinsert(&hp3, repeatData[i]);
    }
    printf("插入重复元素后：");
    PrintHeap(&hp3);  // 预期：堆顶为2，整体满足小堆特性
    printf("依次取堆顶并删除：");
    int heapSize = hpsize(&hp3);
    for (int i = 0; i < heapSize; i++) {
        name1 top = hptop(&hp3);
        printf("%d ", top);  // 预期输出：2 2 3 3 5 5
    }
    printf("\n");

    hpbreak(&hp3);  // 销毁堆
    printf("============================================================\n\n");
}

// 主函数：执行所有测试
int main() {
    TestHeapBasic();        // 测试基础操作
    TestHeapInitFromArr();  // 测试数组初始化堆
    TestHeapEdgeCases();    // 测试边界场景
    return 0;
}

如何实现大堆：

因为我们上面讲的其实主要是实现小堆，那么如果大家要实现大堆，又要怎么办呢？

其实很简单，其他的都不用调整，只需要调整我们的向上调整算法和向下调整算法就OK啦，至于如何实现，下面是详细代码：

要实现大堆，核心是调整向上调整算法 和向下调整算法，其他堆的结构定义、初始化、销毁、插入删除的整体流程无需改变。

向上调整算法（大堆版）

void adjustup_max(name1* arr, int child)
{
    while (child > 0)
    {
        int parent = (child - 1) / 2;
        // 大堆要求父节点大于子节点，若子节点大于父节点则交换
        if (arr[child] > arr[parent])
        {
            swapdata(&arr[child], &arr[parent]);
            child = parent;
        }
        else
        {
            break;
        }
    }
}

向下调整算法（大堆版）

void adjustdown_max(name1* arr, int size, int parent)
{
    int child = parent * 2 + 1;
    while (child < size)
    {
        // 找较大的子节点
        if (child + 1 < size && arr[child] < arr[child + 1])
        {
            child++;
        }
        // 大堆要求父节点大于子节点，若子节点大于父节点则交换
        if (arr[child] > arr[parent])
        {
            swapdata(&arr[child], &arr[parent]);
            parent = child;
            child = parent * 2 + 1;
        }
        else
        {
            break;
        }
    }
}

其他函数适配

• 插入操作（hpinsert）：调用adjustup_max而非adjustup。
• 删除操作（hppop）、数组建堆（hpinitfromarr）：调用adjustdown_max而非adjustdown。

这样，就能将小堆的逻辑修改为大堆，保证堆顶元素始终是最大值。

结语：

当我们合上堆的代码文件，回顾这段从 "陌生" 到 "熟悉" 的学习历程，不难发现，堆绝不仅仅是 "完全二叉树 + 数组存储" 的简单组合，它更像是数据结构设计思想的浓缩 ------ 用最简洁的物理结构（数组）承载最精准的逻辑规则（父子节点大小关系），最终实现高效的核心操作（O (log n) 的插入与删除）。这段学习不仅让我们掌握了一种实用的数据结构，更在潜移默化中培养了 "如何用数学规律优化数据操作""如何用边界条件保障代码健壮性" 的思维能力，而这些，正是从 "会用代码" 到 "懂数据结构" 的关键跨越。

一、堆的 "本质"：不止是代码，更是逻辑的精妙设计

回想最初接触堆时，我们或许会困惑："为什么堆一定要基于完全二叉树？用普通二叉树不行吗？" 如今再看，答案早已清晰 ------ 完全二叉树的 "层序排列、左满右缺" 特性，恰好与数组的 "连续存储、下标有序" 特性完美契合。正是这种契合，让堆无需像链表那样用指针维护节点关系，只需通过parent = (child - 1) / 2"左孩子 = 2parent+1""右孩子 = 2parent+2" 这三个简单的数学公式，就能瞬间定位任意节点的父子关系。这种 "用数学规律替代指针存储" 的设计，既节省了空间（无需额外存储指针），又提升了效率（避免指针跳转的开销），堪称数据结构中 "空间与时间平衡" 的经典案例。

而堆的 "大根堆 / 小根堆" 规则，更体现了 "按需设计" 的思维。当我们需要频繁获取最大值时，大根堆让根节点直接存储最大值，避免了遍历整个数据集的低效；当需要频繁获取最小值时，小根堆则同理。这种 "将核心需求映射到结构设计" 的思路，在实际开发中尤为重要 ------ 比如优先级队列中，任务的紧急程度（优先级）可以直接对应堆中节点的大小，让高优先级任务始终处于堆顶，实现 "随取随用" 的高效调度。

我们在代码中实现的adjustup（向上调整）与adjustdown（向下调整）算法，更是堆逻辑设计的 "灵魂"。向上调整算法针对 "尾插元素破坏堆特性" 的场景，通过 "子节点与父节点逐层比较、交换"，让新元素 "找到自己的位置"------ 它的核心是 "只调整被破坏的路径"（新元素到根节点的路径），而非整个堆，这才保证了 O (log n) 的时间复杂度。而向下调整算法则针对 "堆顶元素删除后堆特性破坏" 的场景，通过 "父节点与较小子节点（小堆）逐层比较、交换"，让新堆顶 "下沉到正确位置"------ 它的前提 "左右子树已为堆" 看似苛刻，实则是算法高效的保障，因为它避免了对无关子树的冗余检查。

这两个算法的实现细节，更藏着 "边界条件" 的严谨性。比如向上调整中child > 0的循环条件，避免了根节点继续寻找父节点导致的下标越界；向下调整中child + 1 < size的判断，防止了右子节点不存在时的非法访问。这些看似微小的细节，恰恰是代码从 "能运行" 到 "能稳定运行" 的关键 ------ 正如我们在测试hpempty（判断堆空）时，若忽略size == 0的判断直接访问arr[0]，就会导致空堆取堆顶的崩溃；在hpinsert（插入元素）时，若忘记size == capacity时的扩容逻辑，就会出现数组越界的严重错误。这些经历让我们深刻明白：数据结构的代码实现，从来不是 "写对逻辑" 就够了，更要 "考虑所有边界"，而堆的学习，正是培养这种严谨性的绝佳载体。

二、堆的 "应用"：从代码到场景，解决问题的高效工具

当我们掌握了堆的基础操作后，再回头看它的应用场景，会发现堆的价值远不止 "存储数据"。比如 "Top K 问题"（从海量数据中找最大 / 最小的 K 个元素），若用普通数组实现，需要先排序（O (n log n)）再取前 K 个元素，而用堆实现，只需维护一个大小为 K 的小堆（找最大 K 个元素）或大堆（找最小 K 个元素），遍历数据时与堆顶比较，符合条件则替换堆顶并调整 ------ 整个过程的时间复杂度仅为 O (n log K)，当 K 远小于 n（如从 100 万数据中找前 100 名）时，效率提升堪称 "量级跨越"。

再比如堆排序，它将堆的特性与排序需求完美结合：先将无序数组构建为大根堆（O (n) 时间），再依次将堆顶（当前最大值）与堆尾元素交换，然后调整堆（O (log n) 时间），重复 n 次后得到升序数组。整个过程无需额外空间（原地排序），时间复杂度稳定为 O (n log n)，且避免了快速排序在极端情况下（如有序数组）退化为 O (n²) 的问题。这些应用让我们意识到：学习数据结构，不能只停留在 "会写结构本身的代码"，更要学会 "将实际问题转化为数据结构能解决的模型"------ 而堆，正是这种 "转化能力" 的优秀训练素材。

我们在测试代码中设计的 "基础操作测试""数组初始化堆测试""边界场景测试"，也暗合了实际开发中 "验证数据结构正确性" 的思路。比如 "基础操作测试" 中，我们通过插入随机数据、观察每次插入后堆顶是否为最小值，验证了hpinsert与adjustup的正确性；"边界场景测试" 中，我们测试空堆、单个元素堆、重复元素堆，覆盖了实际使用中可能遇到的极端情况。这种 "从正常场景到边界场景" 的测试思维，不仅能保障堆的代码正确，更能迁移到其他数据结构的学习中 ------ 比如链表的空链表、单节点链表、循环链表测试，栈的空栈、满栈测试等，成为我们学习数据结构的 "通用方法论"。

三、堆的 "启示"：数据结构学习的 "通用路径"

回顾堆的学习过程，我们其实无意中遵循了一条 "数据结构学习的通用路径"：先理解 "是什么"（堆的定义、结构），再探究 "为什么"（为什么用完全二叉树、为什么用数组存储），然后实践 "怎么做"（实现初始化、插入、删除等操作），最后思考 "用在哪"（Top K、堆排序、优先级队列）。这条路径看似简单，却能帮我们避开 "死记硬背代码" 的误区，真正理解数据结构的本质。

比如在学习hpinitfromarr（用数组初始化堆）时，我们最初可能会想："直接把数组元素复制到堆的数组里，再逐个调用hpinsert不就行了？" 但深入思考后会发现，这种方式的时间复杂度是 O (n log n)（每个元素插入需 O (log n)），而通过 "从最后一个非叶子节点（下标为 (n-2)/2）向前调用adjustdown" 的方式，时间复杂度仅为 O (n)。这种 "不同实现方式的效率对比"，让我们明白：数据结构的学习不仅要 "实现功能"，更要 "优化效率"，而效率的优化，往往源于对数据结构本质的深刻理解 ------ 正是因为我们知道 "adjustdown` 的前提是左右子树已为堆"，所以从非叶子节点向前调整，能让每个节点的调整次数降到最低，最终实现 O (n) 的建堆效率。

再比如我们将小堆修改为大堆时，只需调整adjustup与adjustdown中的比较条件（将arr[parent] > arr[child]改为arr[parent] < arr[child]，将arr[child] > arr[child+1]改为arr[child] < arr[child+1]），其他代码完全复用。这种 "核心逻辑与辅助代码分离" 的设计，体现了 "高内聚、低耦合" 的编程思想 ------ 辅助代码（初始化、销毁、交换、判空）负责 "维护堆的物理结构"，核心算法（调整算法）负责 "维护堆的逻辑规则"，二者互不干扰，既便于修改（如切换大堆 / 小堆），又便于维护（如修复扩容逻辑时无需改动调整算法）。

这些学习中的思考与实践，最终会内化为我们的 "数据结构思维"------ 当我们遇到一个新问题时，不再是 "先想怎么写代码"，而是 "先想数据的特点是什么？核心操作是什么？哪种数据结构能高效支持这些操作？" 比如当遇到 "需要频繁添加任务，并优先处理紧急任务" 的需求时，我们会立刻想到 "优先级队列 = 堆"，因为堆的 "堆顶优先" 特性恰好匹配 "紧急任务优先处理" 的需求；当遇到 "需要从 100 万条日志中找出访问量最高的 10 个 IP" 时，我们会想到 "用大小为 10 的小堆，遍历日志时动态替换堆顶"，因为这种方式比排序整个日志集更高效。

四、堆的 "延伸"：数据结构学习的 "长期价值"

或许有同学会问："在 Python、Java 等高级语言中，已经有现成的堆类（如 Python 的heapq、Java 的PriorityQueue），我们为什么还要亲手实现堆？" 答案其实藏在 "亲手实现" 的过程中 ------ 当我们手动编写hpinit时，会理解 "堆的初始状态为什么要将arr设为NULL、size和capacity设为 0"；当我们调试adjustdown时，会明白 "为什么要先找较小的子节点（小堆），再与父节点比较"；当我们处理realloc扩容失败的perror时，会懂得 "内存分配失败的异常处理对程序稳定性的重要性"。这些细节，是使用现成类库时永远无法触及的，而正是这些细节，构成了 "数据结构素养" 的核心。

更重要的是，堆的学习为我们后续学习更复杂的数据结构（如平衡二叉树、红黑树、图）打下了基础。比如堆的 "调整算法" 与平衡二叉树的 "旋转算法"，本质上都是 "当结构被破坏时，通过局部调整恢复整体特性"；堆的 "父子节点大小关系" 与红黑树的 "颜色规则"，本质上都是 "用明确的规则约束结构，保障操作效率"。可以说，堆的学习，是我们理解 "如何用规则保障效率""如何用局部调整修复全局结构" 的第一堂课，而这些思维能力，会贯穿整个数据结构学习的始终。

回顾这段学习之旅，我们从 "看到堆的代码觉得复杂"，到 "能独立写出堆的初始化、插入、删除"，再到 "能根据需求修改为大堆、能分析堆的应用场景"，每一步都是对 "数据结构思维" 的重塑。我们不再把代码看作 "一行行的指令"，而是看作 "对数据逻辑的描述"；不再把算法看作 "固定的步骤"，而是看作 "解决问题的策略"。这种思维的转变，比 "会用堆" 本身更有价值 ------ 它会让我们在未来学习任何数据结构时，都能快速抓住核心逻辑，理解设计思想，而不是停留在 "死记硬背 API" 的层面。

五、数据结构的世界，永远值得探索

堆的学习告一段落，但数据结构的探索之路才刚刚开始。从简单的数组、链表，到今天的堆，再到未来的平衡二叉树、哈希表、图，每一种数据结构都有其独特的设计思想和应用场景，每一次学习都是对 "如何高效处理数据" 这一核心问题的深入思考。

或许在未来的开发中，我们不会频繁手动实现堆，但这段学习经历留给我们的，是 "用数学规律优化效率""用边界条件保障健壮性""用场景需求选择结构" 的思维习惯。当我们面对复杂问题时，这些习惯会帮助我们快速找到最优解；当我们阅读开源项目的源码时，这些习惯会帮助我们理解底层数据结构的设计逻辑；当我们需要优化系统性能时，这些习惯会帮助我们定位 "数据操作效率低下" 的根源。

最后，想对每一位正在学习数据结构的同学说：不要害怕代码中的细节，不要畏惧算法中的逻辑，因为每一次调试错误、每一次理解规则、每一次优化效率，都是在为自己的 "技术基石" 添砖加瓦。堆只是数据结构世界中的一小步，但只要我们保持这份 "探究本质、精益求精" 的态度，就能在未来的学习中走得更稳、更远。相信终有一天，当我们再看这些数据结构时，看到的不仅是代码，更是解决问题的智慧，是计算机科学中 "简洁与高效" 的永恒追求。

计算机没有眼泪，诸君，共勉！！！！！！