前言
排序算法还是很重要的,虽然有sort() 和 stable_sort(), 但是具体的实现也是数据结构中很重要的一环。
一、排序的一些知识点
排序本身的意义没有什么可以讲的,就是按照关键字的大小,递增或者递减来排列起来的操作。
稳定性:!!! 排完序之后元素的相对次序保持不变,比如原来a[i] == a[j] 并且 a[i]在a[j]之前,那在排序之后a[i]仍然在a[j]之前,这种就是稳定的,否则就是不稳定的。
内部排序:数据放在内存中的排序,学的很多排序都是内部排序
外部排序:数据元素太多不能同时放在内存中,时间集中于磁盘I/O操作,比如多路归并排序。
排序在现实中见的也很多,筛选的时候选项一般也有一个从小到大或者从大到小。
二、常见排序算法
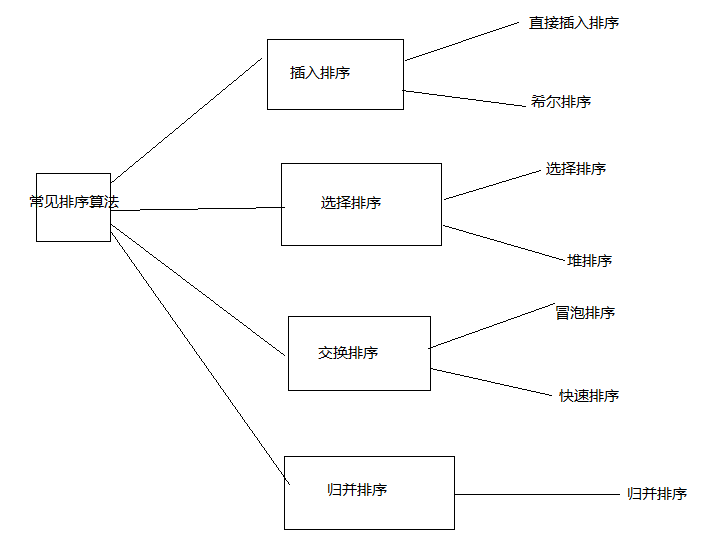
还有一些排序没写在里面,比如桶排序,计数排序,基数排序,也就这十个比较常见的算法,还有一些花里胡哨的比如猴子排序(。后面会简单提一下这三个排序。图里的这七个都是比较排序算法,都有元素的比较,后面介绍的三个就没有比较了。
一、插入排序
1.直接插入排序
a.直接插入排序思路
顾名思义,就是在插入的过程中来排序,当插入第i个元素时,前面的i - 1个已经排好序,此时用arr[i]来跟前面的做比较,找到合适位置插入,之前位置上的元素后移。

(上面这张图片里面演示的是升序,打错了)
b.直接插入排序代码
vector<int> v = {3,1,5,4,2};
//排成降序
void InsertSort(vector<int>& v)
{
for(int i = 1;i < v.size();++i)
{
int data = v[i]; //要插入的数据
int pos = i - 1; // 要比较的元素的位置
while(pos >= 0)
{
if(v[pos] < data)
{
v[pos + 1] = v[pos];
pos--;
}
else break;
}
//这里循环退出表示v[pos] > data 或者 pos = -1,pos + 1就是要插入的位置
v[pos + 1] = data;
}
}c.直接插入排序特点
时间复杂度: O(N ^ 2)
空间复杂度:O(1)
稳定性: 稳定,因为我们写的代码是v[pos] < data就交换,否则就退出
数组如果越接近有序,插入的效率越高。
2.希尔排序
a.希尔排序思路
希尔排序是对直接插入排序的优化,它的思想是:直接插入的数据越接近有序效率越高???那我直接先进行几次预排序让其部分有序怎么样,它的思路是先选取一个gap,将a[0],a[0 + gap],a[0 + 2 * gap]直到下标大于n为止,先将这一部分进行直接插入排序,然后gap - - ,我们发现当gap == 1的时候这就是直接插入排序!!!!
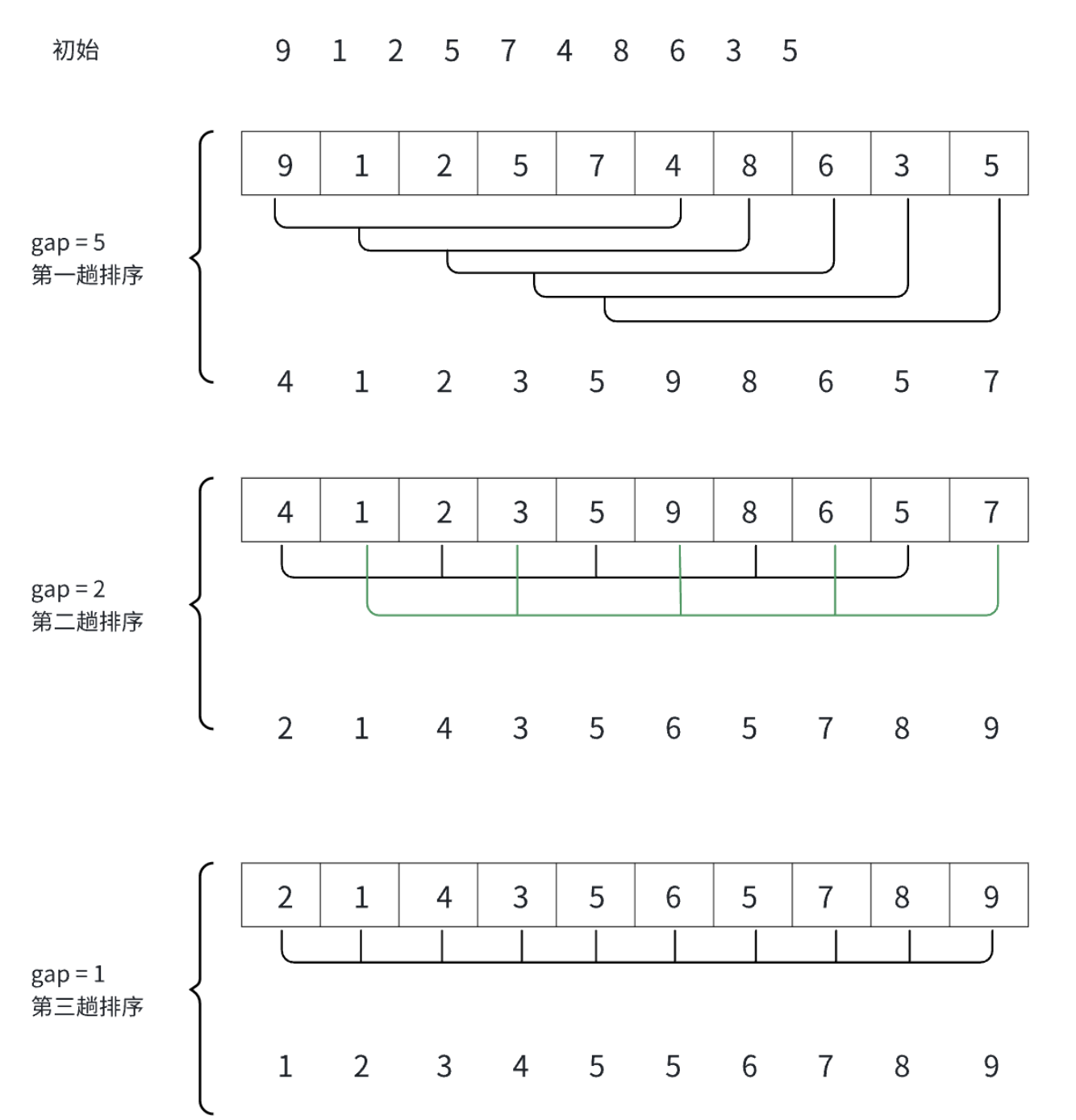
gap越大,跳的越快,越不接近有序
gap越小,跳的越慢,越接近有序
gap也可以这样选取,gap = n,每次让gap / 3 + 1,直到gap <= 1为止,这样gap也一定会到1
b.希尔排序代码
void InsertSort(vector<int>& v)
{
for(int gap = 3;gap >= 1;gap--)
{
for(int i = 0;i + gap < v.size();++i)
{
int data = v[i + gap];
int pos = i;
while(pos >= 0)
{
if(v[pos] < data)
{
v[pos + gap] = v[pos];
pos -= gap;
}
else break;
}
v[pos + gap] = data;
}
}
}c.希尔排序特点:
1.希尔排序是对直接插入排序的优化
2.gap > 1都是预排序,让数组接近有序,gap == 1才是真正的排序,这样整体到达优化的效果
3.稳定性:不稳定,由于分组排序,相对位置完全会变。
时间复杂度:这个是一个复杂的问题,暂时没有定论,gap = [gap /3 ] + 1,这么取的时间复杂度应该是n ^ 1.25 到 1.6 * n ^ 1.25, 希尔的暂时定为n ^ 1.3
二、选择排序
基本思想:顾名思义,就是每一次选择最大或者最小的元素,放在数组首位,其他依次放置,直到数组有序为止。
1.直接选择排序
a.直接选择排序思路
1.每一次从arr[i]到arr[n - 1]中选择关键码最大或者最小的元素
2.如果他不是这组元素的最后一个或者第一个元素,则交换
3.在剩下的元素中,重复上述步骤,直到集合剩余一个元素为止。
b.直接选择排序代码
因为我们要操作的是下标,所以这里的maxi代表的就是下标i。 当然下面这个代码可以优化,一次循环找出最大和最小的元素,分别放在左边和右边,然后往中间收缩。
//降序
void SelectSort(vector<int>& v)
{
int n = v.size();
int l = 0,r = n;
int maxi = 0;
while(l < n)
{
maxi = l;
for(int i = l + 1;i < n;++i) if(v[maxi] < v[i]) maxi = i;
swap(v[l++],v[maxi]);
}
}优化:
void SelectSort(vector<int>& v)
{
int n = v.size();
int l = 0,r = n - 1;
int maxi = 0,mini = n - 1;
while(l < r)
{
maxi = l,mini = l;
for(int i = l + 1;i <= r;++i)
{
if(v[maxi] < v[i]) maxi = i;
if(v[mini] > v[i]) mini = i;
}
if(l == mini) mini = maxi;
swap(v[l],v[maxi]);
swap(v[r],v[mini]);
l++,r--;
}
}这里判断l == mini的意义是什么? ? ?
如果要排的是降序,你找到的最小在l处,但是v[l]要和v[maxi]交换!
不做这个处理下面交换代码的意义就可能变成: 第一次swap: l 处变成了最大的,第二次swap: v[r]要和最小的交换,但是mini的位置已经变成了最大的了! 这样就会出问题,所以这个就是做判断的理由。
c.直接选择排序特点
1.直接排序算法是非常差的算法,因为时间复杂度稳定在O(N ^ 2),即使是排好序的数组也是这样。
2.时间复杂度稳定在O(N ^ 2)
3.空间复杂度O(1)
4.稳定性:不稳定,因为要选择出来并且去交换。
2.堆排序
a.堆排序思路
堆排序是基于堆的基础上进行的排序。
思路:如果要排成降序,建立小堆,升序建立大堆。第一次:将堆顶元素和最后一个元素交换,然后将堆顶元素向下调整,第二次:堆顶元素和倒数第二个元素交换 ... ... ... ... . ...直到堆顶元素交换到自身为止。
这样为什么可以排序? 比如升序建立的大堆,堆顶元素一定是最大的,那他和最后一个元素交换之后就一定是最大的,其余同理。为什么不能建立小堆?想一想就知道了,无法控制大小关系。
所以就是需要先建堆再排序。只需要向下调整就可以了。
注意:这里需要控制堆的大小,因为排序的过程中每次排好一个元素他都不需要参与建堆了,如果最后一个元素还参与的话就会导致这个元素又调整上去了,所以:建堆的时候大小就是数组长度,排序的时候大小就是最后一个元素的下标了。
b.堆排序代码
void Adjustdown(vector<int>& v,int parent,int HeapSize)
{
int child = parent * 2 + 1, n = v.size();
while(child < HeapSize)
{
if(child + 1 < HeapSize && v[child + 1] < v[child]) child++;
if(v[child] < v[parent])
{
swap(v[child],v[parent]);
parent = child;
child = parent * 2 + 1;
}
else break;
}
}
void HeapSort(vector<int>& v)
{
//先进行建堆
int n = v.size();
for(int i = (n - 1 - 1) / 2;i >= 0;--i) Adjustdown(v,i,n);
Print(v);
//然后进行选择排序
int end = n - 1;
while(end)
{
swap(v[0],v[end]);
Adjustdown(v,0,end);
--end;
}
}c.堆排序特点
1.时间复杂度:O(N * logN)
2.空间复杂度:O(1)
3.稳定性: 不稳定
三、交换排序
基本思想就是交换,根据两个元素的键值的比较大小来进行交换,比如排升序,就是键值较大的向尾部移动,键值较小的向首部移动。
1.冒泡排序
a.冒泡排序思路
冒泡排序的思路比较简单也好理解,就是一次排完之后排好一个元素的位置,每趟排好的元素是当前未排序部分的最后一个元素。这里不过多介绍了,应该都会。
b.冒泡排序代码
这里注意控制好i和j的取值范围,外层的i表示趟数,n - 1次即可排好,内层的i表示具体两个元素的比较,由于每一次都排好了一个元素,所以只需要比较前n - i个元素就可以。
下面写的代码都是降序排列的
cpp
void Bubble_Sort(vector<int>&v)
{
int n = v.size();
for(int i = 0; i < n - 1;++i)
{
for(int j = 0;j < n - 1 - i;++j)
{
if(v[j] < v[j + 1]) swap(v[j],v[j + 1]);
}
}
for(int i = 0;i < n;++i)
{
cout << v[i] << ' ';
}
}当然,在cstdlib这个头文件中也有qsort,指的就是冒泡排序。
cpp
int compare(const void* p1,const void* p2)
{
return (*(int*)p1) < (*(int*)p2);
}
int main()
{
qsort(arr,sizeof(arr) / sizeof(int),sizeof(int),compare);
for(int i = 0;i < 5;++i) cout << arr[i] << endl;
return 0;
}compare是个函数指针,给void*的原因就是这样适配所有类型,因为C语言没有模板。
优化:上述代码有一个问题,如果说我的数组已经有序了但是竟然又发生了一趟比较,这样就是浪费时间了。所以我可以记录一个bool a,如果一次交换都没发生说明已经排好序了,就直接break.
优化代码:
cpp
void Bubble_Sort(vector<int>&v)
{
int n = v.size();
bool a = false;
for(int i = 0; i < n - 1;++i)
{
a = true;
for(int j = 0;j < n - 1 - i;++j)
{
if(v[j] < v[j + 1]) swap(v[j],v[j + 1]),a = false;
}
if(a) break;
}
}c.冒泡排序特点
1.时间复杂度: 最差情况:O(n ^ 2),最好情况:O(N),平均情况:O(N ^ 2)
2.空间复杂度:O(1)
3.稳定性:稳定
冒泡排序不如直接插入排序,直接插入排序是越来越接近有序,效率更高。
2.快速排序
由于快速排序东西较多,所以额外写一篇文章来介绍了。
个人文章:
四、归并排序
a.归并排序思路
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 其中还有多路归并排序,这里介绍一下二路归并排序。
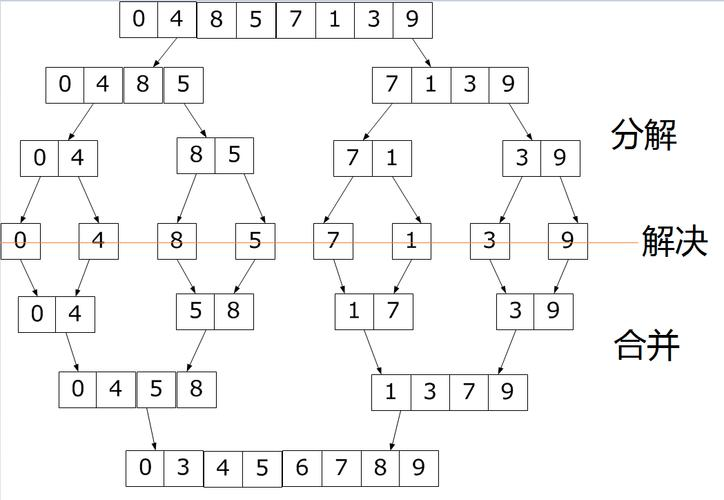
b.归并排序代码 ---递归版
思路:
写代码的思路是什么? 快速排序是先用partion得到div,再去递归左右区间,而归并呢?归并是先细分到0,4再一层一层返回,比如细分到17 39怎么合成???这里有个细节:每个小区间都已经是有序的了!!!那我能在原数组上操作吗?当然不能!没法操作下标,所以需要一个数组,每一次都写在数组里然后拷贝回去!
代码:
不太懂的可以看一看我代码的注释加深一下理解
cpp
void Memcpy(vector<int>&dest,vector<int>&src,int begin,int size)
{
for(int i = begin;i <= begin + size - 1;++i)
{
dest[i] = src[i];
}
}
void _MergeSort(vector<int>&v,int left,int right,vector<int>&v1)
{
if(left >= right) return ;
int mid = (left + right) / 2;
_MergeSort(v,left,mid,v1);
_MergeSort(v,mid + 1,right,v1);
//不断细分区间,细分到这说明该进行归并排序了,要处理[left,right]的元素
int begin1 = left,end1 = mid;
int begin2 = mid + 1,end2 = right;
//细分好了每一个区间,有序拷贝到v1里,哪个区间??? [left,mid] [mid + 1,right]
//又因为无法对left,right直接操作,所以定义变量
int i = left;
while(begin1 <= end1 && begin2 <= end2)
{
if(v[begin1] < v[begin2]) v1[i++] = v[begin1++];
else v1[i++] = v[begin2++];
}
//剩了元素怎么办? ?填进去
//下面这两个while循环只会执行一次,因为上面的while退出来就需要一个不满足条件
while(begin1 <= end1) v1[i++] = v[begin1++];
while(begin2 <= end2) v1[i++] = v[begin2++];
//拷贝给原数组
Memcpy(v,v1,left,right - left + 1);
}
void MergeSort(vector<int>&v)
{
vector<int> v1;
v1.resize(v.size());
_MergeSort(v,0,v.size() - 1,v1);
}这个代码确实是所有排序里比较不好写的了,还有个非递归更有点难写,但是理解过程了递归的写法还是可以想出来的。
b.归并排序代码---非递归版
所有的递归都能改成非递归,这个怎么改呢? ? ?
思路:
既然要先分解成小区间再合并回去,这次同样需要begin1,end1,begin2,end2
,但是这里不是递归,没法用mid控制,所以需要定义一个gap,gap的含义: 一个区间的长度是gap,最开始gap = 1,直到gap >= n退出循环,相当于最开始[begin1,end1] 是第一个元素,这样就可以处理区间了,那我们怎么处理其他区间呢,用i来控制,一次处理了2 * gap个区间,每次让i += 2 * gap即可,一次完成后gap *= 2,代表区间长度乘2。
清晰思路:1. 定义gap, gap = 1,直到gap >= n 跳出循环 while(gap < n)
2.内部定义,i --for(int i = 0;i < n;i += gap * 2)
3.begin1 = i,end1 = i + gap - 1,begin2 = i + gap,end2 = i + gap * 2 - 1,这样确保了每个区间的长度都是gap----这里有问题要处理
4.和递归的思路一样,排序给v1
5.拷贝回原数组
ps:对于拷贝,可以在for循环内部拷贝,也可以在while循环内部拷贝,只不过拷贝的size不一样,对于for循环内部拷贝,每一次相当于处理了2 * gap个区间拷贝回去,也就是end2 - i + 1,起点是i,对于while循环内部,相当于每次处理了整个数组,分成了每个区间长度都是gap,理解这个就好写了。
下面解决第三条的问题,这里end1,begin2,end2有可能>= n啊,需要处理
1.如果end1 >= n怎么办,说明begin2 和end2早就大于等于n了,后面没有处理的必要,begin2和end2设置成不存在的区间即可,而end1自然设计成n - 1
2.begin2 >= n,与1类似,begin2和end2设计成不存在的区间即可
3.end2 >= n说明此时begin2 < n,end2 设计成n - 1即可。
代码 (一次拷贝2 * gap个长度)
cpp
void MergeSortNoneRe(vector<int> &v)
{
int gap = 1, n = v.size();
vector<int> v1;
v1.resize(n);
// i i + gap - 1, i + gap,i + 2 *gap - 1
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap,end2 = i + 2 * gap - 1;
//确认区间是否在范围内
if(end1 >= n)
{
end1 = n - 1;
begin2 = n,end2 = n - 1;
}
else if(begin2 >= n)
{
begin2 = n,end2 = n - 1;
}
else if(end2 >= n)
{
end2 = n - 1;
}
//开始拷贝
int j = i;
while(begin1 <= end1 && begin2 <= end2)
{
if(v[begin1] < v[begin2]) v1[j++] = v[begin1++];
else v1[j++] = v[begin2++];
}
//begin1 或者 begin2未完
while(begin1 <= end1) v1[j++] = v[begin1++];
while(begin2 <= end2) v1[j++] = v[begin2++];
//拷贝回去
//这里不能使用begin,因为begin是++了的.
Memcpy(v,v1,i,(end2 - i + 1));
}
gap *= 2;
}
}一次拷贝整个数组
在gap *= 2下面加上这个就可以了.
cpp
Memcpy(v,v1,0,n);优化
我们发现,当end1>=n和begin2>=n的时候对原数组没有进行任何的操作,因为第二个区间不存在,没有需要合并的区间,所以直接break即可
cpp
if(end1 >= n || begin2 >= n) break;c.归并排序特点
- 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决磁盘中的外排序问题。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定--stable_sort()
非比较排序算法
一、计数排序
a.计数排序思路
计数排序本质是对哈希直接定址法的应用,思想就是哈希
将数组最小值到最大值的范围映射到另一个数组下标中,再对另一个数组依次统计即可。比较简单和好想
b.计数排序代码
cpp
void CountSort(vector<int>&v)
{
int maxi = *max_element(v.begin(),v.end());
int mini = *min_element(v.begin(),v.end());
vector<int> v1;
v1.resize(maxi - mini + 1);
for(int i = 0;i < v.size();++i)
{
v1[v[i] - mini] ++; //映射
}
int j = 0; //下标
//这里的v1[i]代表的是出现次数,i + mini才是本来的值
for(int i = 0;i < v1.size();++i)
{
while(v1[i]--) v[j++] = i + mini;
}
}c.计数排序特点
1.时间复杂度: O(max(N,maxi- mini + 1)),这个就决定了计数排序更加使用于小范围数据,且小范围数据效率很高。
2.空间复杂度O(maxi - mini + 1)
3.稳定性:稳定
二、桶排序
a.桶排序思路
桶排序的思路也是一种哈希,类似拉链法,将N个数,映射到十个桶内(数量自己定),再对每一个桶进行排序,最后组合起来,有点像计数但是不太一样。 怎么映射? num / 10 即可,这样可以初步分出大小,再进行排序组合就完成了。
ps:有负数怎么办?好办,求出数组中的最小值,小于0就让所有数加一个,让所有数大于等于0再排,最后再减回来。
b.桶排序代码
cpp
void BucketSort(vector<int>& v)
{
const int cnt = 10; // 桶的个数
int mini = *min_element(v.begin(),v.end());
if(mini < 0){
for(auto&e:v) e -= mini;
}
vector<vector<int>> vv(cnt);
for(int i = 0;i < v.size();++i)
{
int num = v[i] / 10;
vv[num].push_back(v[i]);
}
for(int i = 0;i < vv.size();++i)
{
sort(vv[i].begin(),vv[i].end());
//小数据也可以用插入排序
}
int j = 0;
for(int i = 0;i < vv.size();++i)
{
for(int num: vv[i])
{
v[j++] = num + mini;
}
}
}c.桶排序特点
1.时间复杂度: O(N + K),最坏N ^ 2,最好N,这么认为就可以,K为基数
2.空间复杂度:O(N)
3,稳定性:稳定
三、基数排序
a.基数排序思路
基数排序是基于桶排序的一种排序,基数排序是开十个桶,也只能开十个桶,代表0到9,依次对个位、十位...进行排序,直到超过了最大数,统计数目,负数和上面同理。
b.基数排序代码
cpp
void CardinalSort(vector<int>&v)
{
int mini = *min_element(v.begin(),v.end());
if(mini < 0) for(auto&e:v) e -= mini;
int maxi = *max_element(v.begin(),v.end());
int d = 1;
while(d < maxi)
{
vector<vector<int>> vv(10);
for(int i = 0;i < v.size();++i)
{
int num = (v[i] / d) % 10;
vv[num].push_back(v[i]);
}
//将这些数据拷贝给原数组
int j = 0;
for(int i = 0;i < vv.size();++i)
{
for(auto &e:vv[i]) v[j++] = e;
}
d *= 10;
}
if(mini < 0) for(auto&e:v) e += mini;
}c.基数排序特点
1.时间复杂度:O(d * (n + k)),d是数组中最大数的位数,k是基数,十进制下为10,2进制下为2
2.空间复杂度:O(n + k)
3.稳定性:稳定
总结
这些算法中后三个了解即可,快速和归并比较重要,前七个算法需要能准确的知道时间复杂度、空间复杂度、稳定性、原理。
数据结构终于告一段落了,准备开始写操作系统的博客。