引入
在算法刷题的广阔领域中，数组类问题始终占据着重要地位，它们常常围绕"元素选择""条件筛选"等核心逻辑展开。这类问题不仅考察开发者对数组遍历、排序、条件判断等基础操作的掌握程度，更注重解题思路的合理性与效率的最优化。本文将聚焦 LeetCode 上两个典型的数组问题------"2500. 删除每行中的最大值"与"2951. 找出峰值"，从问题本质出发，细致拆解解题逻辑，深入解析代码实现的每一处细节，并拓展相关的知识点与进阶应用场景。无论你是刚踏入算法领域的初学者，还是希望巩固数组操作基础的开发者，通过本文的学习，都能进一步提升对数组类问题的掌控力，掌握"排序优化"与"条件筛选"的核心思想，为攻克更复杂的算法难题积累宝贵经验。
一、2500. 删除每行中的最大值
1.1 问题描述与分析
1.1.1 问题描述
给你一个 m x n 大小的矩阵 grid，由若干正整数组成。执行下述操作，直到 grid 变为空矩阵：
从每一行删除值最大的元素。如果存在多个这样的值，删除其中任何一个。
将删除元素中的最大值与答案相加。
注意每执行一次操作，矩阵中列的数据就会减 1。返回执行上述操作后的答案。
1.1.2 示例与分析
示例（假设输入）
grid = [[1,2,4],[3,3,1]]
操作过程：
第一次操作：每行删除最大值（第一行删 4，第二行删 3），删除元素的最大值是 4，sum = 4；矩阵变为 [[1,2],[3,1]]。
第二次操作：每行删除最大值（第一行删 2，第二行删 3），删除元素的最大值是 3，sum = 4 + 3 = 7；矩阵变为 [[1],[1]]。
第三次操作：每行删除最大值（两行都删 1），删除元素的最大值是 1，sum = 7 + 1 = 8；矩阵变为空。
最终返回 8。
1.1.3 核心需求与约束
核心需求：通过多次"每行删最大值，累加删除元素的最大值"的操作，直到矩阵为空，最终得到累加和。
关键观察：每次操作需要获取每行的当前最大值，再从这些最大值中取最大的进行累加。若对每行进行排序，每行的最大值会处于固定位置（如升序排序后每行的最后一位），后续按列遍历可高效获取每行当前最大值。
约束条件：矩阵由正整数组成，操作次数等于矩阵的列数（每次操作列数减 1，直到列数为 0）。
1.2 解题思路演进
1.2.1 排序 + 按列遍历策略
核心思路：先对矩阵的每一行进行升序排序，使每行的最大值位于行的末尾。之后按列遍历矩阵，每一列中取各行的元素（即每行当前的最大值），将这些元素的最大值累加到结果中。
java
class Solution {
public int deleteGreatestValue(int[][] grid) {
for (int i = 0; i < grid.length; i++) {
Arrays.sort(grid[i]);
}
int sum = 0;
for (int c = 0; c < grid[0].length; c++) {
int currentMax = 0;
for (int r = 0; r < grid.length; r++) {
currentMax = Math.max(currentMax, grid[r][c]);
}
sum += currentMax;
}
return sum;
}
}1.2.2 复杂度分析
时间复杂度：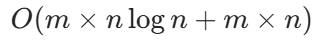
，其中 m是矩阵的行数，n 是矩阵的列数。对每一行排序的时间复杂度为 O(n log n)，共 m 行，排序总时间为
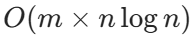；按列遍历矩阵，外层循环n次，内层循环m次，时间复杂度是 
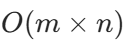。整体由排序操作主导。
空间复杂度O(log n)，源于排序过程的辅助空间开销（Java 中 Arrays.sort 对基本类型数组采用双轴快速排序，空间复杂度为 O(log n)）。
该方法逻辑清晰高效，通过排序将"每行找最大值"的操作从 O(n) 优化为 O(1)，大幅降低时间开销。
1.3 代码逐句解析
java
class Solution {
public int deleteGreatestValue(int[][] grid) {
// 遍历每一行，对行内元素进行升序排序
for (int i = 0; i < grid.length; i++) {
Arrays.sort(grid[i]);
}
// 初始化累加和 sum
int sum = 0;
// 按列遍历，c 表示当前列索引
for (int c = 0; c < grid[0].length; c++) {
// 初始化当前列的最大值 currentMax
int currentMax = 0;
// 遍历每一行，r 表示当前行索引
for (int r = 0; r < grid.length; r++) {
// 更新当前列的最大值
currentMax = Math.max(currentMax, grid[r][c]);
}
// 将当前列的最大值累加到 sum
sum += currentMax;
}
// 返回最终累加和
return sum;
}
}1.3.1 关键细节说明
Arrays.sort(grid[i])：对每行升序排序，确保每行最大值位于行的最后一位（grid[i][n-1]），后续按列遍历时，grid[r][c] 即为第 r 行第 c 次操作时的最大值。
按列遍历次数：等于矩阵的列数 grid[0].length，因每次操作删除一列元素，操作次数与列数一致。
列内最大值获取：通过内层循环遍历每一行的当前列元素，用 Math.max 逐步更新得到该列最大值，此值为本次操作需累加的数值。
1.4 排序与数组遍历知识拓展
1.4.1 排序算法的选择与适用场景
本题使用 Java 内置的 Arrays.sort（底层双轴快速排序）对每行排序。快速排序平均时间复杂度 O(n log n)，空间复杂度 O(log n)，在多数场景下是数组排序的最优选择之一。
适用场景：需对数组全排序且数据规模适中（如本题每行的列数 n）时，快速排序性能高效。
其他排序算法对比：
冒泡、插入排序：时间复杂度 O(n^2)，n 较大时性能极差，不适用于本题。
归并排序：时间复杂度 O(nlog n)，但空间复杂度 O(n)，相比快速排序空间开销更大，本题无需额外空间优化，故快速排序更优。
1.4.2 二维数组的遍历方式
本题采用"按列遍历"方式，需确保每一行长度相同（矩阵规整）。按列遍历外层循环控制列，内层循环控制行，虽缓存友好性稍差，但逻辑上贴合"每次操作处理一列"的需求。
按行遍历 vs 按列遍历：
按行遍历：外层循环控制行，内层循环控制列，缓存友好性更好（数组在内存中按行连续存储）。
按列遍历：外层循环控制列，内层循环控制行，本题因逻辑需要采用，需保证矩阵规整。
1.5 测试用例分析
测试用例输入 grid |
输出 | 说明 |
|---|---|---|
[[1,2,4],[3,3,1]] |
8 | 三次操作累加 4、3、1 |
[[5]] |
5 | 只有一行一列，一次操作直接累加 5 |
[[1,1,1],[1,1,1],[1,1,1]] |
3 | 每次操作删除的最大值都是 1，共三列，累加 1+1+1=3 |
[[10,8,6],[5,4,3],[2,1,0]] |
24 | 排序后每行升序为 [6,8,10]、[3,4,5]、[0,1,2]；按列累加 10+5+2=24 |
二、2951. 找出峰值
2.1 问题描述与分析
2.1.1 问题描述
给你一个下标从 0 开始的数组 mountain。你的任务是找出数组 mountain 中的所有峰值。以数组形式返回给定数组中峰值的下标，顺序不限。
注意：
峰值是指一个严格大于其相邻元素的元素。
数组的第一个和最后一个元素不是峰值。
2.1.2 示例与分析
示例：
输入：mountain = [2,4,1,5,3]
输出：[1,3]
解释：下标 1（元素 4，左右是 2 和 1，严格大于）、下标 3（元素 5，左右是 1 和 3，严格大于）是峰值。
2.1.3 核心需求与约束
核心需求：筛选出数组中所有"严格大于左右相邻元素"的元素下标，且排除数组首尾元素。
关键观察：对于下标 i（1 ≤ i ≤ mountain.length - 2`），只需判断 mountain[i] > mountain[i-1] 且 mountain[i] > mountain[i+1] 即可确定是否为峰值。
约束条件：数组长度至少为 3 才可能存在峰值（否则首尾占满，无中间元素），若数组长度小于 3，直接返回空数组。
2.2 解题思路演进
2.2.1 线性遍历筛选策略
核心思路：遍历数组中所有可能的下标（从 1 到 mountain.length - 2），对每个下标 i 判断是否满足"严格大于左右相邻元素"的条件，若满足则将下标加入结果列表。
java
class Solution {
public List findPeaks(int[] mountain) {
ArrayList peaks = new ArrayList<>();
for (int i = 1; i < mountain.length - 1; i++) {
if (mountain[i] > mountain[i-1] && mountain[i] > mountain[i+1]) {
peaks.add(i);
}
}
return peaks;
}
}2.2.2 复杂度分析
时间复杂度：O(n)，其中 n 是数组 mountain 的长度。只需遍历一次数组的中间元素（从下标 1 到 n-2），每次判断为 O(1)操作，总时间复杂度为线性级别。
空间复杂度：O(1)（不考虑结果列表的存储，若考虑则为 O(p)，其中 p 是峰值的数量p ≤ n/2）。
该方法逻辑直观、实现简单，且时间复杂度最优，因要判断每个中间元素是否为峰值，必须至少遍历一次所有中间元素，线性时间复杂度是该问题的下限。
2.3 代码逐句解析
java
class Solution {
public List findPeaks(int[] mountain) {
ArrayList peaks = new ArrayList<>();
for (int i = 1; i < mountain.length - 1; i++) {
if (mountain[i] > mountain[i-1] && mountain[i] > mountain[i+1]) {
peaks.add(i);
}
}
return peaks;
}
}2.3.1 关键细节说明
循环范围：i 的取值范围是 [1, mountain.length - 2]，确保只判断中间元素，排除首尾元素（题目规定首尾不是峰值）。
严格大于的条件：必须同时满足 mountain[i] > mountain[i-1] 和 mountain[i] > mountain[i+1]，"严格大于"是题目明确要求，若写成"大于等于"会错误包含非峰值元素。
结果列表的顺序：题目允许返回顺序不限，直接按遍历顺序添加即可，无需额外排序。
2.4 条件筛选与数组边界知识拓展
2.4.1 边界条件的重要性
在数组类问题中，边界条件的处理是出错高频点。本题中：
若数组长度小于 3（如 mountain.length < 3），循环不会执行，直接返回空列表，符合"首尾不是峰值，无中间元素"的逻辑。
若数组长度等于 3（如 [1,3,2]），只需判断下标 1 的元素是否为峰值，逻辑正确。
实际开发中处理数组时需时刻关注"索引越界"问题，确保循环的起始和终止条件严格符合逻辑需求。
2.4.2 类似问题的条件变种
本题核心是"严格大于左右"的条件，实际场景中存在多种变种，需根据需求调整判断逻辑：
大于等于左，严格大于右：适用于"山脉数组"中找峰顶的场景（如 LeetCode 852. 山脉数组的峰顶索引）。
严格大于左，大于等于右：可用于某些"下降沿"前的峰值判断。
大于左右其中一个：适用于找"局部极大值"（不要求严格大于两者）的场景。
2.5 测试用例分析
测试用例输入 mountain |
输出 | 说明 |
|---|---|---|
[2,4,1,5,3] |
[1,3] |
下标 1（4>2 且 4>1）、下标 3（5>1 且 5>3）是峰值 |
[1,2,3,4,5] |
[] |
无元素严格大于右邻居，无峰值 |
[5,4,3,2,1] |
[] |
无元素严格大于左邻居，无峰值 |
[1,5,3,6,4,7,2] |
[1,3,5] |
下标 1（5>1 且 5>3）、下标 3（6>3 且 6>4）、下标 5（7>4 且 7>2）是峰值 |
[3] |
[] |
数组长度小于 3，无峰值 |
三、两个问题的异同与总结
3.1 相同点分析
数组操作核心：均以数组（或二维数组）为基础数据结构，解题依赖数组的遍历操作，体现了数组作为线性结构在算法问题中的通用性。
条件判断关键：都需要通过明确的条件判断来筛选元素或确定操作逻辑（"每行最大值的列最大值""严格大于左右元素"），条件判断的准确性直接影响代码正确性。
时间复杂度优化：均通过合理的遍历策略或预处理（如排序）将时间复杂度优化至线性或线性对数级别，避免了低效的嵌套循环（如 O(n^2) 复杂度）。
3.2 不同点分析
| 特征 | 删除每行中的最大值（2500） | 找出峰值（2951） |
|---|---|---|
| 数据结构维度 | 二维数组（矩阵） | 一维数组 |
| 核心算法思想 | 排序优化 + 按列遍历 | 线性筛选 + 条件判断 |
| 时间复杂度主导因素 | 排序操作（\(O(m \times n \log n)\)） | 线性遍历（\(O(n)\)） |
| 空间复杂度 | \(O(\log n)\)（排序辅助空间） | \(O(1)\)（或 \(O(p)\)，p 为峰值数量） |
| 适用场景拓展 | 矩阵元素的批量筛选与累加 | 一维序列的特征点（峰值）识别 |
3.3 编程思想提炼
排序的价值：在"删除每行中的最大值"问题中，排序将"动态找最大值"转化为"静态取固定位置元素"，大幅降低后续遍历的时间开销，体现了"预处理优化后续操作"的编程思想。
条件筛选的严谨性：在"找出峰值"问题中，严格的条件判断（`mountain[i] > mountain[i-1] && mountain[i] > mountain[i+1]`）是确保结果正确的关键，要求开发者精准理解题目定义（如"严格大于""首尾排除"）。
问题抽象能力：将实际问题抽象为数组的遍历、排序、条件判断等基础操作，是解决算法问题的核心能力。例如，将"矩阵操作"抽象为"每行排序后按列取最大值累加"，将"找峰值"抽象为"遍历中间元素并判断左右大小"。
3.4 拓展练习与进阶思考
3.4.1 2500. 删除每行中的最大值 拓展
进阶问题：若矩阵中的元素可能为负数，且操作改为"删除每行中的最小值，累加删除元素中的最小值"，如何调整解法？
思路：将"升序排序"改为"降序排序"（或升序排序后取行的首位元素），之后按列遍历取每行的当前最小值（即排序后行的首位元素），再累加这些最小值中的最小值。
代码示例：
java
class Solution {
public int deleteSmallestValue(int[][] grid) {
for (int i = 0; i < grid.length; i++) {
Arrays.sort(grid[i]);
reverse(grid[i]);
}
int sum = 0;
for (int c = 0; c < grid[0].length; c++) {
int currentMin = Integer.MAX_VALUE;
for (int r = 0; r < grid.length; r++) {
currentMin = Math.min(currentMin, grid[r][c]);
}
sum += currentMin;
}
return sum;
}
private void reverse(int[] arr) {
int left = 0, right = arr.length - 1;
while (left < right) {
int temp = arr[left];
arr[left] = arr[right];
arr[right] = temp;
left++;
right--;
}
}
}3.4.2 2951. 找出峰值 拓展
进阶问题：若数组是环形的（即第一个元素的左邻居是最后一个元素，最后一个元素的右邻居是第一个元素），如何找出所有峰值？
思路：调整边界条件，对于下标 0，其左邻居是 mountain.length - 1，右邻居是 1；对于下标 mountain.length - 1，其左邻居是 mountain.length - 2，右邻居是 0；中间下标仍判断左右相邻元素。
代码示例：
java
class Solution {
public List findCircularPeaks(int[] mountain) {
ArrayList peaks = new ArrayList<>();
int n = mountain.length;
for (int i = 0; i < n; i++) {
int left = (i - 1 + n) % n;
int right = (i + 1) % n;
if (mountain[i] > mountain[left] && mountain[i] > mountain[right]) {
peaks.add(i);
}
}
return peaks;
}
}3.4.3 进阶思考
数据规模与算法选择：当二维数组的行数m和列数n都达到 10^4 时，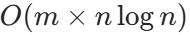
的排序操作是否可行？若不可行，是否有更高效的方法？
分析：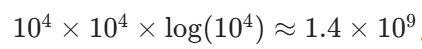
，在时间限制严格的场景下可能超时。若数据规模极大，需结合问题其他特性（如元素范围）进行优化。
多条件峰值判断：若峰值的定义改为"大于左邻居或大于右邻居"，如何高效统计此类"局部极大值"的数量？
思路：遍历数组时，对每个元素（除首尾外）判断 mountain[i] > mountain[i-1] || mountain[i] > mountain[i+1]，统计满足条件的元素数量，时间复杂度仍为 O(n)。
3.5 总结
本文对"2500. 删除每行中的最大值"与"2951. 找出峰值"两个 LeetCode 数组问题从问题描述、思路演进、代码细节到知识拓展进行了全方位解析。
"删除每行中的最大值"展示了**排序优化**在数组操作中的强大作用，通过排序将动态操作转化为静态操作，大幅提升算法效率。"找出峰值"体现了线性筛选与条件判断的核心思想，通过遍历和严格条件判断精准筛选峰值元素。
两个问题均强调**问题本质拆解**与**边界条件处理**的重要性。只有准确理解问题核心需求与约束条件，才能选择最适合的算法，写出高效且健壮的代码。
希望读者通过本文学习，不仅掌握这两个问题的解题方法，更能培养"从问题到算法"的思维链路，在面对其他算法问题时能逐步推进，提升解决实际问题的能力。