神经网络 - 循环神经网络

01 序列数据

时间序列数据指在不同时间点收集的数据，反映某一事物或现象随时间变化的状态或程度。

序列数据不一定随时间变化（如文本序列），但所有序列数据都有一个共同特征：后序数据与前序数据存在关联。

序列数据的应用场景

语音识别
音乐生成
情感分类
DNA序列分析
机器翻译
视频动作识别
命名实体识别

序列顺序的重要性 ：

"我""去""购物中心""打车"四个词，不同顺序表达不同含义：

正确语义："我打车去购物中心"
语义偏差："我去购物中心打车"

02 循环神经网络（RNN）

发展历程

感知机（1958）→ 长短期记忆网络（LSTM，1997）→ 深度游走（Deepwalk，2014）、序列到序列模型（Seq2Seq，2017）→ 注意力机制（2017）→ Transformer（2017）→ BERT/GPT（2018）

核心思想

通过"循环连接"让网络保留历史信息，即当前时刻的隐藏状态不仅依赖当前输入，还依赖上一时刻的隐藏状态，从而处理序列数据。

关键公式

隐藏状态更新 ：
ht=fW(ht−1,xt)h_{t}=f_{W}\left(h_{t-1}, x_{t}\right)ht=fW(ht−1,xt)

其中，hth_tht 为 ttt 时刻的隐藏状态（记忆），ht−1h_{t-1}ht−1 为 t−1t-1t−1 时刻的隐藏状态，xtx_txt 为 ttt 时刻的输入，fWf_WfW 为带参数 WWW 的非线性函数（如tanh）。
具体计算（tanh激活） ：
ht=tanh⁡(Whhht−1+Wxhxt)h_{t}=\tanh \left(W_{hh} h_{t-1}+W_{xh} x_{t}\right)ht=tanh(Whhht−1+Wxhxt)

其中，WhhW_{hh}Whh 为隐藏状态间的权重矩阵，WxhW_{xh}Wxh 为输入到隐藏状态的权重矩阵。
输出计算 ：
yt=Whyhty_{t}=W_{hy}h_tyt=Whyht

其中，yty_tyt 为 ttt 时刻的输出，WhyW_{hy}Why 为隐藏状态到输出的权重矩阵。

RNN的处理是逐时刻迭代 的，每个时刻ttt的计算遵循以下公式：

{ht=tanh⁡(Wxhxt+Whhht−1+bh)yt=softmax(Whyht+by) \begin{cases} h_t = \tanh\left( W_{xh} x_t + W_{hh} h_{t-1} + b_h \right) \\ y_t = \text{softmax}\left( W_{hy} h_t + b_y \right) \end{cases} {ht=tanh(Wxhxt+Whhht−1+bh)yt=softmax(Whyht+by)

WxhW_{xh}Wxh：输入到隐藏层的权重矩阵；
WhhW_{hh}Whh：隐藏层到隐藏层的权重矩阵（循环连接的核心，实现"历史状态传递"）；
WhyW_{hy}Why：隐藏层到输出层的权重矩阵；
bh,byb_h, b_ybh,by：偏置项；
tanh⁡\tanhtanh：隐藏层的激活函数（也可使用ReLU、sigmoid等）；
softmax\text{softmax}softmax：输出层的激活函数（用于分类任务，如语言模型的词概率预测）。

步骤1：初始隐藏状态（h0h_0h0）

在处理序列的第一个元素（t=1t=1t=1）时，需要初始化隐藏状态h0h_0h0。通常初始化为全0向量，表示"无历史信息"。

步骤2：时刻t=1t=1t=1的计算

输入：x1x_1x1（序列的第一个元素）
隐藏状态：h1=tanh⁡(Wxhx1+Whhh0+bh)h_1 = \tanh\left( W_{xh} x_1 + W_{hh} h_0 + b_h \right)h1=tanh(Wxhx1+Whhh0+bh)（融合当前输入和初始状态）
输出：y1=softmax(Whyh1+by)y_1 = \text{softmax}\left( W_{hy} h_1 + b_y \right)y1=softmax(Whyh1+by)（根据当前隐藏状态预测结果）

步骤3：时刻t=2t=2t=2的计算

输入：x2x_2x2（序列的第二个元素）
隐藏状态：h2=tanh⁡(Wxhx2+Whhh1+bh)h_2 = \tanh\left( W_{xh} x_2 + W_{hh} h_1 + b_h \right)h2=tanh(Wxhx2+Whhh1+bh)（融合当前输入和上一时刻的隐藏状态h1h_1h1）
输出：y2=softmax(Whyh2+by)y_2 = \text{softmax}\left( W_{hy} h_2 + b_y \right)y2=softmax(Whyh2+by)

步骤4：迭代至序列结束

重复上述过程，直到处理完序列的所有元素（t=Tt=Tt=T，TTT为序列长度）。最终，隐藏状态hTh_ThT包含了整个序列的信息 ，输出yTy_TyT是对整个序列的最终预测（如情感分析的"正面/负面"）或对最后一个元素的预测（如语言模型的下一个词）。

栗子

输入序列（input sequence）：

11\]\[11\]\[22\] \\left\[ \\begin{array}{c} 1 \\\\ 1 \\end{array} \\right\] \\left\[ \\begin{array}{c} 1 \\\\ 1 \\end{array} \\right\] \\left\[ \\begin{array}{c} 2 \\\\ 2 \\end{array} \\right\] \[11\]\[11\]\[22

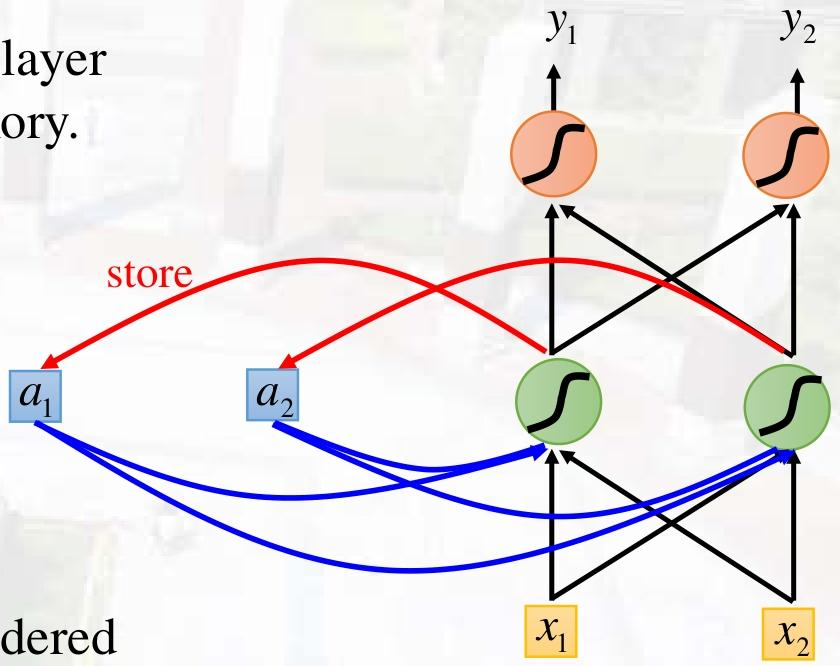
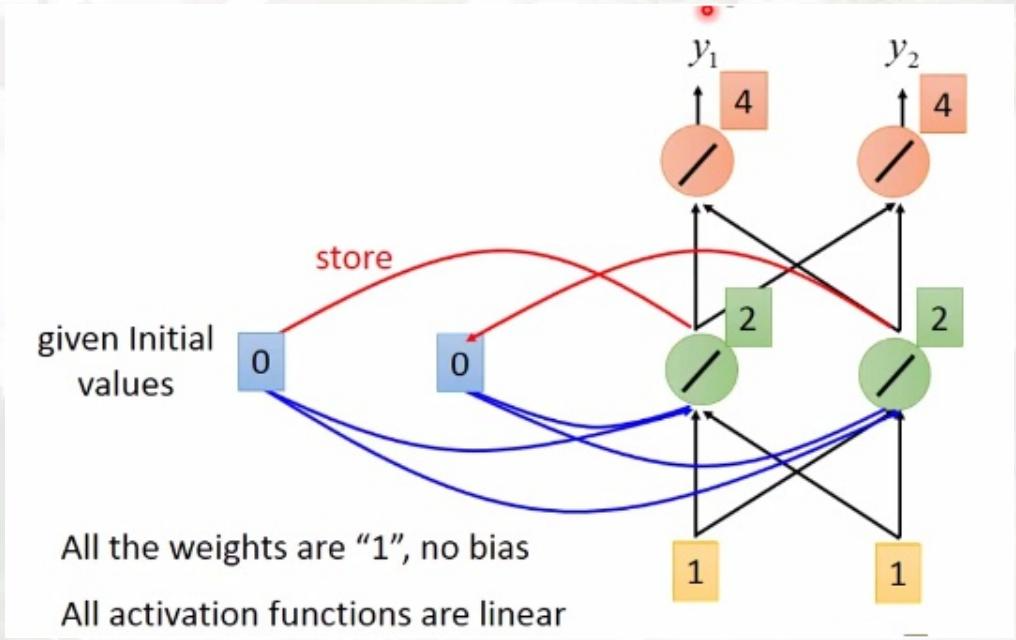
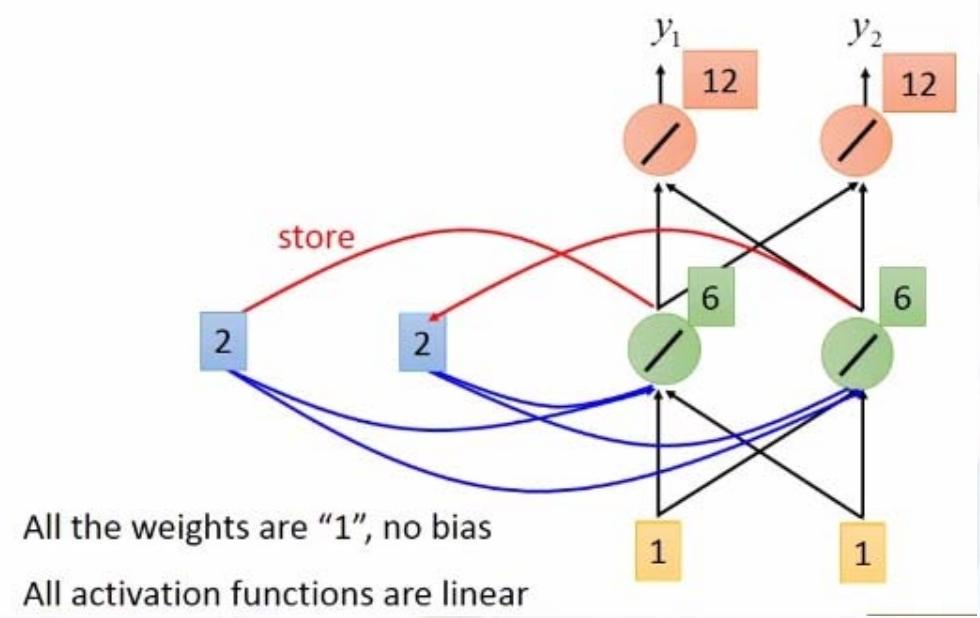
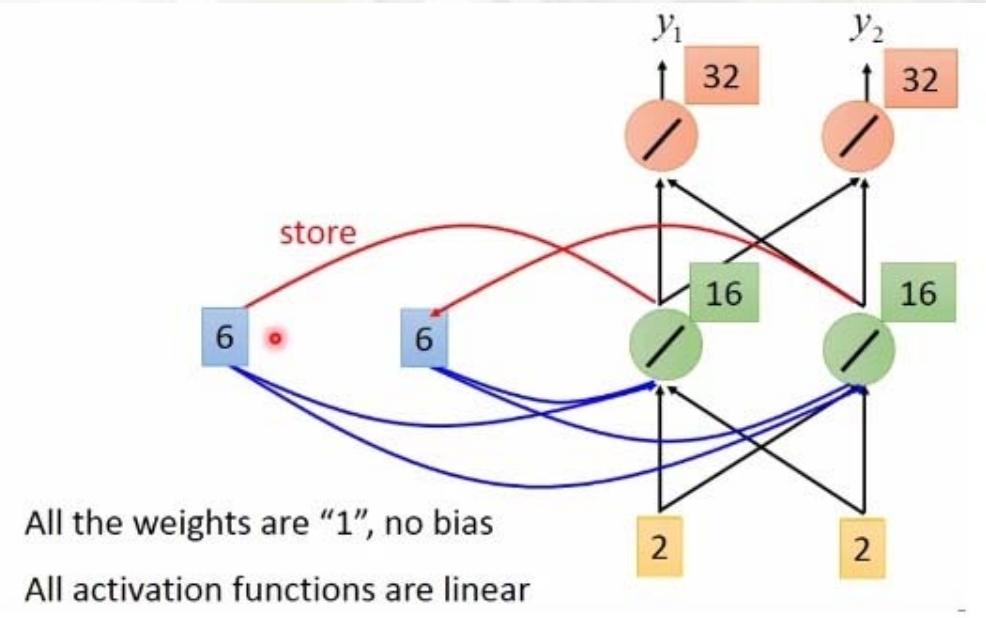
输出序列（Output sequence）：

44\]\[1212\]\[3232\] \\left\[ \\begin{array}{c} 4 \\\\ 4 \\end{array} \\right\] \\left\[ \\begin{array}{c} 12 \\\\ 12 \\end{array} \\right\] \\left\[ \\begin{array}{c} 32 \\\\ 32 \\end{array} \\right\] \[44\]\[1212\]\[3232

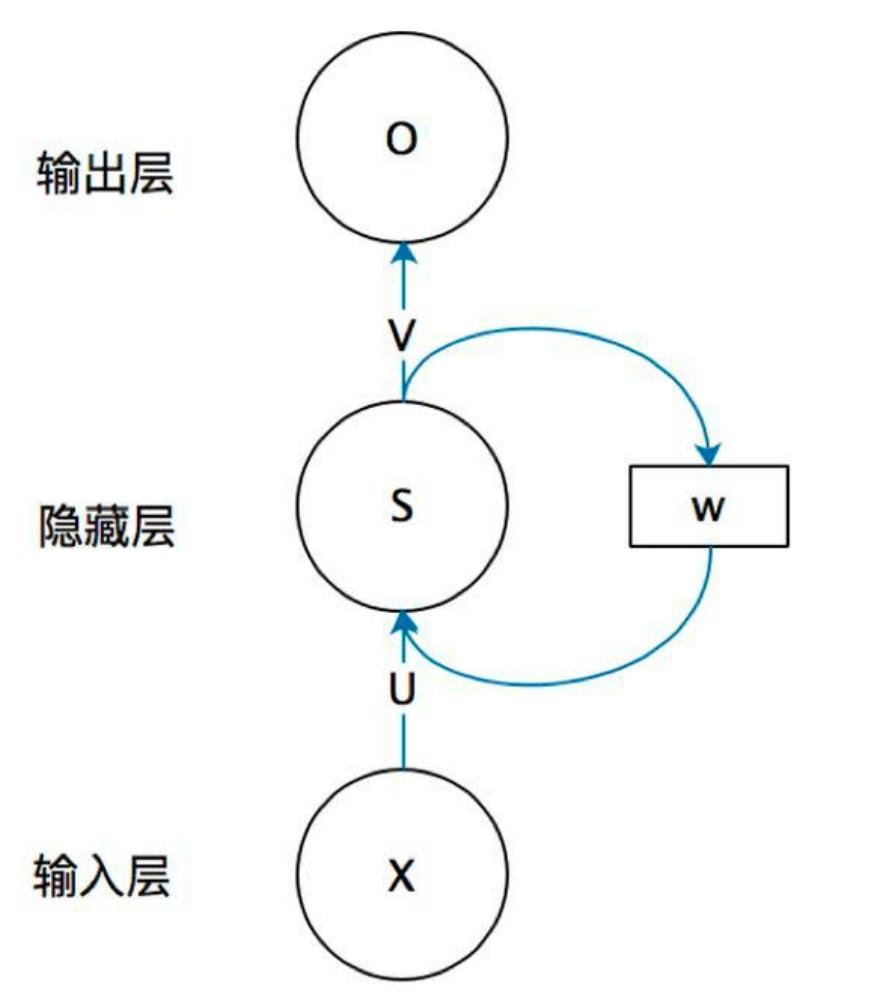
网络结构（按时间展开）

层级	符号与含义
输入层	XXX：输入层神经元值（如 XtX_tXt 为 ttt 时刻输入）
隐藏层	SSS：隐藏层神经元值（St=f(U⋅Xt+W⋅St−1)S_t = f(U \cdot X_t + W \cdot S_{t-1})St=f(U⋅Xt+W⋅St−1)，UUU 为输入到隐藏层权重）
循环层	WWW：隐藏层到自身的循环权重（实现历史信息传递）
输出层	OOO：输出层神经元值（Ot=g(V⋅St)O_t = g(V \cdot S_t)Ot=g(V⋅St)，VVV 为隐藏层到输出层权重）

核心特点 ：不同时间步共享同一套参数（U、W、VU、W、VU、W、V），减少参数数量，提升泛化能力。

计算图与序列处理模式

RNN通过"时间展开"将循环结构转化为链式结构，支持4种序列处理模式：

模式	输入输出关系	应用场景示例
一对一（One-to-One）	单个输入→单个输出	图像分类（非序列任务）
一对多（One-to-Many）	单个输入→序列输出	图像描述生成（图→文字序列）、音乐生成
多对一（Many-to-One）	序列输入→单个输出	情感分类（文字序列→情感标签）、视频动作识别
多对多（Many-to-Many）	序列输入→序列输出	机器翻译（文字序列→文字序列）、帧级视频分类

字符级语言模型示例（以"hello"为例）

词汇表 ：[h,e,l,o][h, e, l, o][h,e,l,o]（共4个字符）。
输入序列 ："h""e""l""l""o"（每个字符用独热向量表示，如"h"为[1,0,0,0][1,0,0,0][1,0,0,0]）。
隐藏状态计算 ：
每个时间步根据上一时刻隐藏状态（初始为0）和当前输入更新隐藏状态，如：
h1=tanh⁡(Whh⋅0+Wxh⋅x1)h_1=\tanh \left(W_{hh} \cdot 0 + W_{xh} \cdot x_1\right)h1=tanh(Whh⋅0+Wxh⋅x1)（x1x_1x1 为"h"的独热向量）。
输出与预测 ：
输出层通过 yt=Whyhty_t = W_{hy}h_tyt=Whyht 计算每个字符的预测概率（经Softmax归一化），训练目标是让预测字符与真实目标字符（如输入"h"时，目标为"e"）一致。
测试阶段采样 ：
从第一个字符（如"h"）开始，将模型预测的字符作为下一时刻输入，循环生成序列（如"h"→"e"→"l"→"l"→"o"）。

03 时间反向传播算法（BPTT）

核心问题：长程依赖

当序列较长时，RNN难以利用早期时间步的信息（如句子"I grew up in France... I speak fluent ()"中，括号处应填"French"，但早期"France"的信息易被后续信息"冲淡"），根源是梯度消失/爆炸问题。

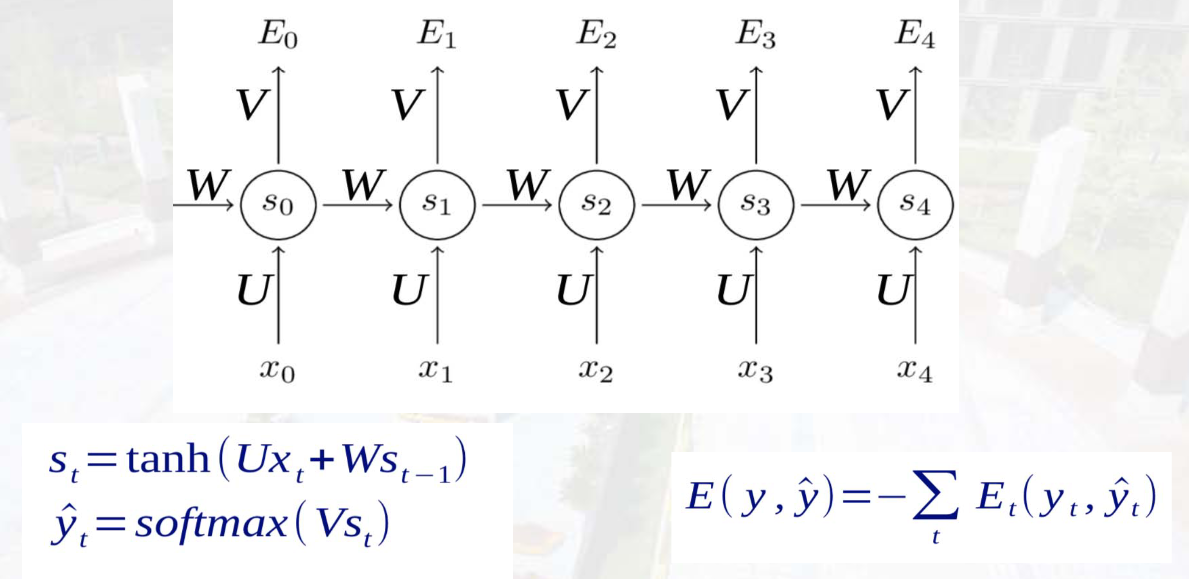
梯度计算与问题推导

损失函数 ：

总损失为各时间步损失之和：E(y,y^)=−∑tEt(yt,y^t)E(y, \hat{y})=-\sum_{t} E_{t}\left(y_{t}, \hat{y}_{t}\right)E(y,y^)=−∑tEt(yt,y^t)，其中 EtE_tEt 为 ttt 时刻的损失（如交叉熵损失），y^t=softmax(Vst)\hat{y}_t = \text{softmax}(V s_t)y^t=softmax(Vst)（sts_tst 为隐藏状态）。
权重梯度计算 ：

以权重 WWW（隐藏层循环权重）为例，t=3t=3t=3 时刻损失对 WWW 的梯度为：
∂E3∂W=∑k=03∂E3∂y^3∂y^3∂s3(∏j=k+13∂sj∂sj−1)∂sk∂W\frac{\partial E_{3}}{\partial W}=\sum_{k=0}^{3} \frac{\partial E_{3}}{\partial \hat{y}{3}} \frac{\partial \hat{y}{3}}{\partial s_{3}} \left(\prod_{j=k+1}^{3} \frac{\partial s_{j}}{\partial s_{j-1}}\right) \frac{\partial s_{k}}{\partial W}∂W∂E3=k=0∑3∂y^3∂E3∂s3∂y^3 j=k+1∏3∂sj−1∂sj ∂W∂sk

其中，∏j=k+13∂sj∂sj−1\prod_{j=k+1}^{3} \frac{\partial s_{j}}{\partial s_{j-1}}∏j=k+13∂sj−1∂sj 为梯度传递中的"连乘项"。

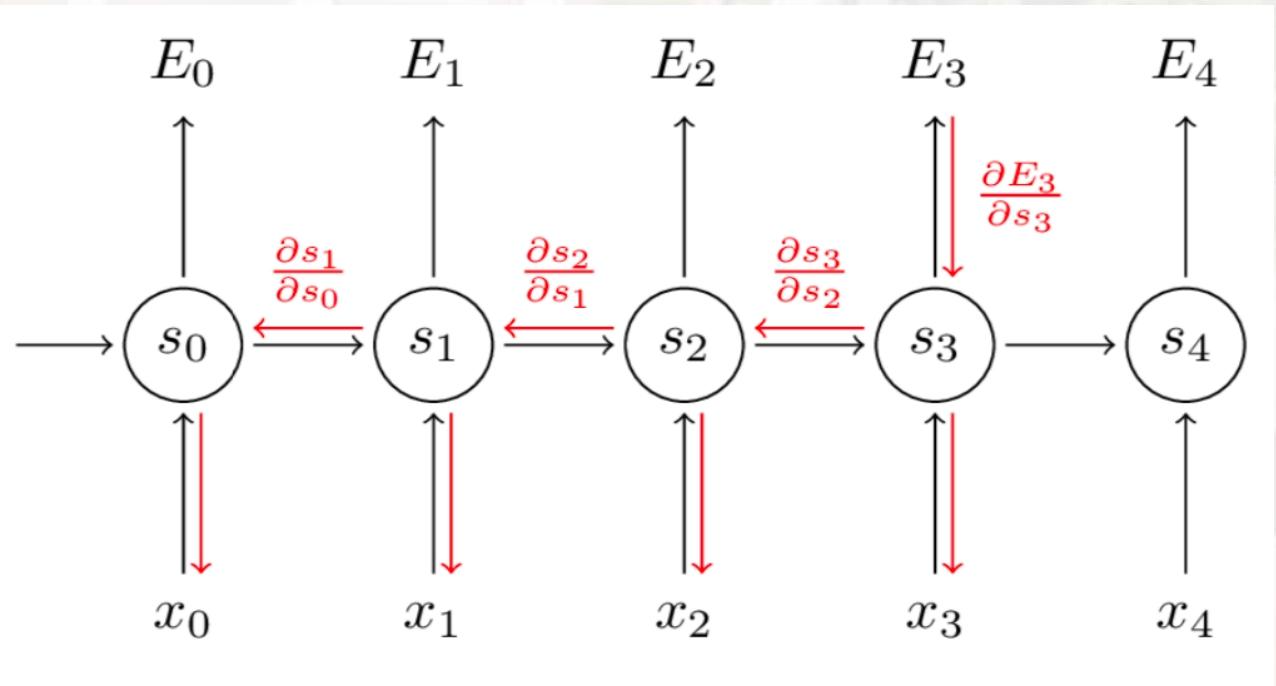
要推导这个梯度公式，我们需要结合**时间反向传播（BPTT）**的链式法则，逐步分析损失对循环权重 WWW 的依赖关系。以下是详细推导过程：

步骤1：明确符号与依赖关系

E3E_3E3：第3时刻的损失（如交叉熵损失）；
y^3\hat{y}_3y^3：第3时刻的模型输出；
sjs_jsj：第 jjj 时刻的隐藏状态（由前一时刻隐藏状态 sj−1s_{j-1}sj−1 和当前输入 xjx_jxj 计算得到）；
WWW：循环权重（隐藏层到自身的权重矩阵，控制历史隐藏状态的传递）。

我们的目标是计算 ∂E3∂W\frac{\partial E_3}{\partial W}∂W∂E3，即第3时刻的损失对循环权重 WWW 的梯度。

步骤2：应用链式法则分解梯度

根据链式法则，损失 E3E_3E3 对 WWW 的梯度可分解为：
∂E3∂W=∂E3∂y^3⋅∂y^3∂s3⋅∂s3∂W+∂E3∂y^3⋅∂y^3∂s3⋅∂s3∂s2⋅∂s2∂W+∂E3∂y^3⋅∂y^3∂s3⋅∂s3∂s2⋅∂s2∂s1⋅∂s1∂W+∂E3∂y^3⋅∂y^3∂s3⋅∂s3∂s2⋅∂s2∂s1⋅∂s1∂s0⋅∂s0∂W \frac{\partial E_3}{\partial W} = \frac{\partial E_3}{\partial \hat{y}_3} \cdot \frac{\partial \hat{y}_3}{\partial s_3} \cdot \frac{\partial s_3}{\partial W} + \frac{\partial E_3}{\partial \hat{y}_3} \cdot \frac{\partial \hat{y}_3}{\partial s_3} \cdot \frac{\partial s_3}{\partial s_2} \cdot \frac{\partial s_2}{\partial W} + \frac{\partial E_3}{\partial \hat{y}_3} \cdot \frac{\partial \hat{y}_3}{\partial s_3} \cdot \frac{\partial s_3}{\partial s_2} \cdot \frac{\partial s_2}{\partial s_1} \cdot \frac{\partial s_1}{\partial W} + \frac{\partial E_3}{\partial \hat{y}_3} \cdot \frac{\partial \hat{y}_3}{\partial s_3} \cdot \frac{\partial s_3}{\partial s_2} \cdot \frac{\partial s_2}{\partial s_1} \cdot \frac{\partial s_1}{\partial s_0} \cdot \frac{\partial s_0}{\partial W} ∂W∂E3=∂y^3∂E3⋅∂s3∂y^3⋅∂W∂s3+∂y^3∂E3⋅∂s3∂y^3⋅∂s2∂s3⋅∂W∂s2+∂y^3∂E3⋅∂s3∂y^3⋅∂s2∂s3⋅∂s1∂s2⋅∂W∂s1+∂y^3∂E3⋅∂s3∂y^3⋅∂s2∂s3⋅∂s1∂s2⋅∂s0∂s1⋅∂W∂s0

这个分解的核心逻辑是：损失 E3E_3E3 依赖 s3s_3s3，而 s3s_3s3 又依赖 s2s_2s2、s1s_1s1、s0s_0s0（每个时刻的隐藏状态都由前一时刻隐藏状态和循环权重 WWW 计算）。因此，梯度需要沿着时间反向传播，考虑所有历史时刻对当前损失的影响。

步骤3：合并同类项并引入求和与连乘符号

观察上述分解式，我们可以将其整理为求和形式 ，其中每一项对应"从时刻 kkk 开始，反向传播到时刻3"的梯度贡献：

∂E3∂W=∑k=03(∂E3∂y^3⋅∂y^3∂s3⋅∏j=k+13∂sj∂sj−1⋅∂sk∂W) \frac{\partial E_3}{\partial W} = \sum_{k=0}^{3} \left( \frac{\partial E_3}{\partial \hat{y}3} \cdot \frac{\partial \hat{y}3}{\partial s_3} \cdot \prod{j=k+1}^{3} \frac{\partial s_j}{\partial s{j-1}} \cdot \frac{\partial s_k}{\partial W} \right) ∂W∂E3=k=0∑3 ∂y^3∂E3⋅∂s3∂y^3⋅j=k+1∏3∂sj−1∂sj⋅∂W∂sk

求和项 ∑k=03\sum_{k=0}^{3}∑k=03 ：表示对所有可能的"起始时刻 kkk"（从0到3）进行累加；
连乘项 ∏j=k+13∂sj∂sj−1\prod_{j=k+1}^{3} \frac{\partial s_j}{\partial s_{j-1}}∏j=k+13∂sj−1∂sj ：表示从时刻 k+1k+1k+1 到时刻3，隐藏状态对前一时刻隐藏状态的偏导数的连乘（即梯度在时间上的传递）；
剩余项 ∂E3∂y^3⋅∂y^3∂s3⋅∂sk∂W\frac{\partial E_3}{\partial \hat{y}_3} \cdot \frac{\partial \hat{y}_3}{\partial s_3} \cdot \frac{\partial s_k}{\partial W}∂y^3∂E3⋅∂s3∂y^3⋅∂W∂sk ：分别对应"损失对输出的梯度""输出对当前隐藏状态的梯度""时刻 kkk 隐藏状态对循环权重 WWW 的梯度"。

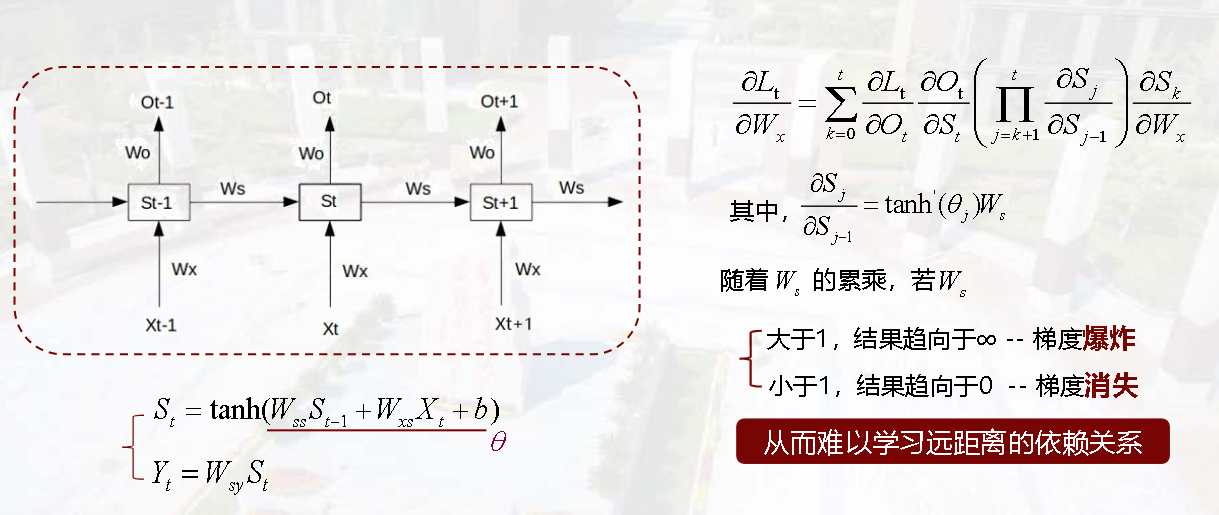
步骤4：解释梯度消失/爆炸的根源

在RNN中，隐藏状态的更新通常使用tanh激活函数，即 sj=tanh⁡(Wsj−1+Uxj)s_j = \tanh(W s_{j-1} + U x_j)sj=tanh(Wsj−1+Uxj)（UUU 是输入到隐藏层的权重）。此时，∂sj∂sj−1=tanh⁡′(Wsj−1+Uxj)⋅W\frac{\partial s_j}{\partial s_{j-1}} = \tanh'(W s_{j-1} + U x_j) \cdot W∂sj−1∂sj=tanh′(Wsj−1+Uxj)⋅W。

若 tanh⁡′(⋅)\tanh'(\cdot)tanh′(⋅) 的绝对值小于1，且 WWW 的谱范数（最大特征值）也小于1，那么连乘项 ∏j=k+13∂sj∂sj−1\prod_{j=k+1}^{3} \frac{\partial s_j}{\partial s_{j-1}}∏j=k+13∂sj−1∂sj 会指数级衰减 ，导致早期时刻（如 k=0k=0k=0）的梯度贡献几乎为0，即梯度消失；
若 WWW 的谱范数大于1，连乘项会指数级增长，导致梯度爆炸。

梯度消失/爆炸原因 ：
- 若使用tanh激活函数，∂sj∂sj−1=tanh⁡′(⋅)⋅W\frac{\partial s_j}{\partial s_{j-1}} = \tanh'(\cdot) \cdot W∂sj−1∂sj=tanh′(⋅)⋅W，tanh导数的绝对值≤1，多次连乘后梯度会"指数级缩小"（梯度消失）；
- 若权重矩阵 WWW 的特征值大于1，连乘后梯度会"指数级增大"（梯度爆炸）。

04 长短期记忆网络（LSTM）

核心改进：解决长程依赖

通过引入记忆单元（Cell State） 和三门结构（遗忘门、输入门、输出门） ，实现对信息的"选择性遗忘"和"选择性存储"，缓解梯度消失问题。

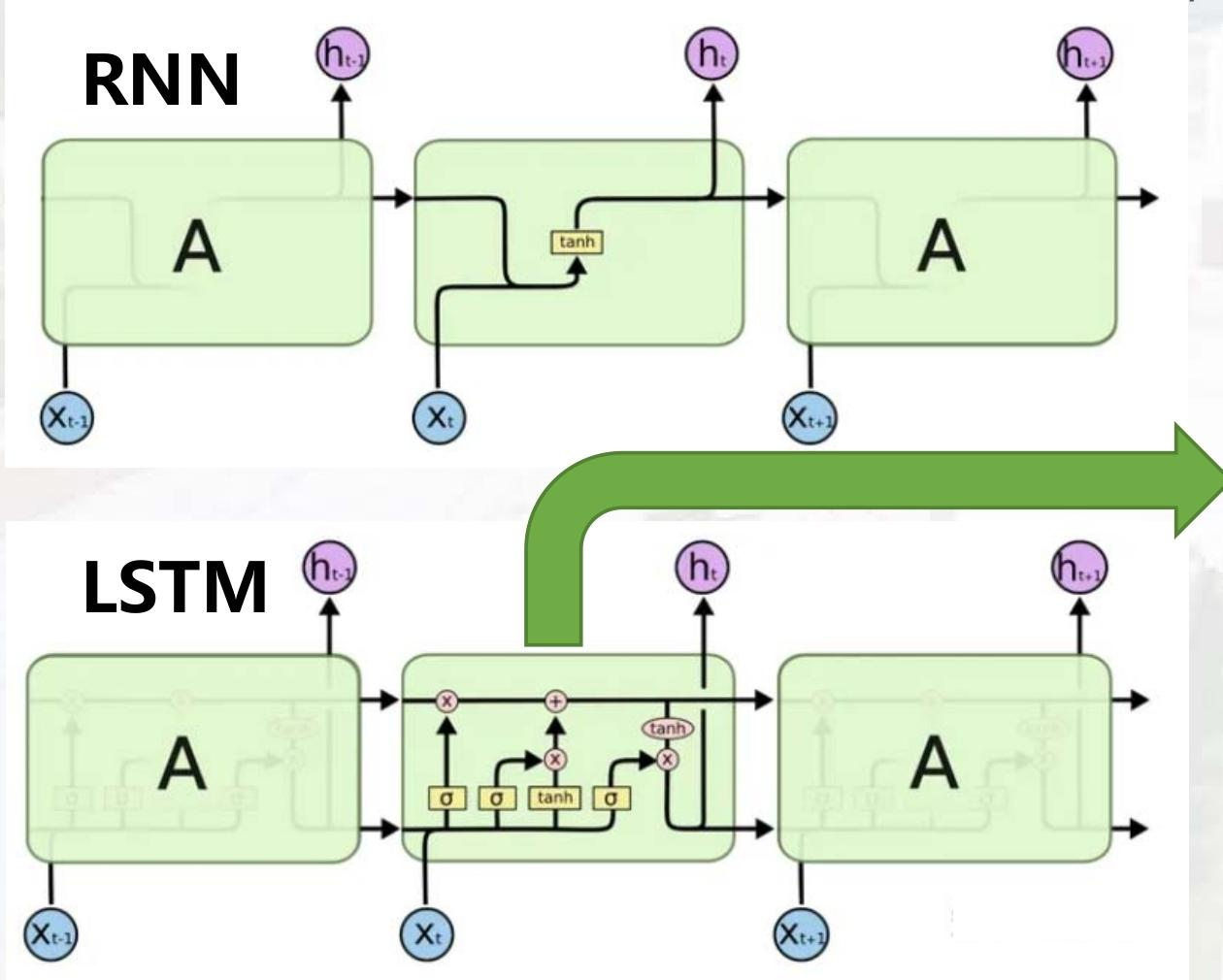
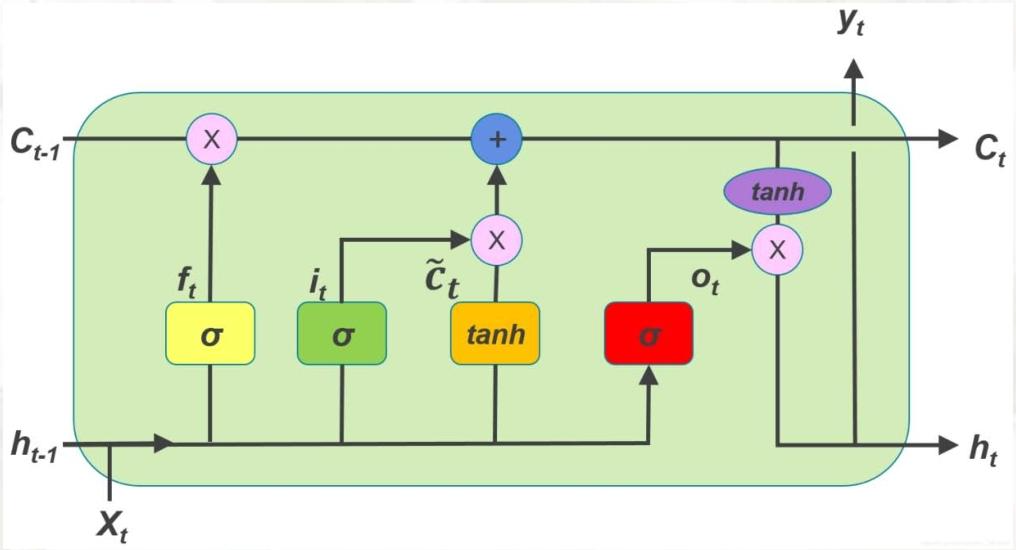
关键结构与公式

1. 遗忘门（Forget Gate）

作用：决定从记忆单元中丢弃哪些信息。
计算：ft=σ(Wf⋅[ht−1,xt]+bf)f_{t}=\sigma\left(W_{f} \cdot\left[h_{t-1}, x_{t}\right]+b_{f}\right)ft=σ(Wf⋅[ht−1,xt]+bf)
其中，σ\sigmaσ 为sigmoid函数（输出0-1，0表示完全丢弃，1表示完全保留），[ht−1,xt][h_{t-1}, x_t][ht−1,xt] 表示将 ht−1h_{t-1}ht−1 与 xtx_txt 拼接，WfW_fWf 为遗忘门权重，bfb_fbf 为偏置。

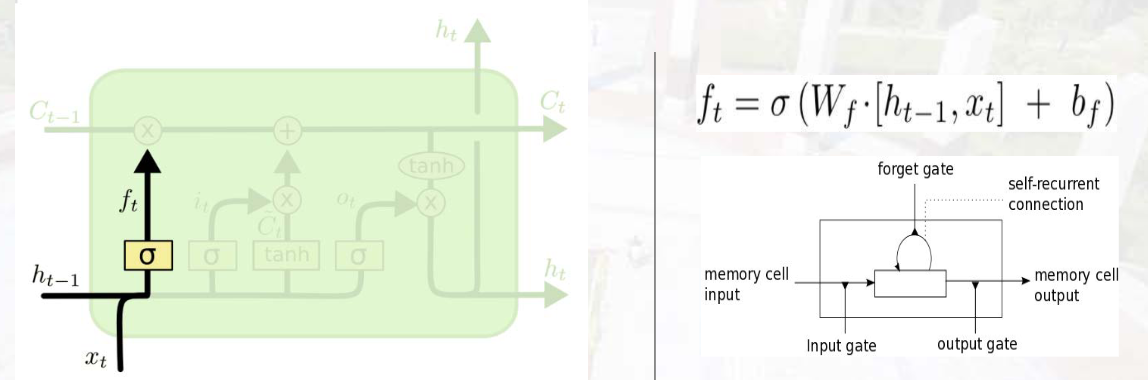
遗忘门计算短时记忆信息与当前信息的关系，用sigmoid映射到[0,1]，得到抛弃短时记忆的程度。

2. 输入门（Input Gate）

作用：决定哪些新信息存入记忆单元。
计算：
① 筛选更新信息：it=σ(Wi⋅[ht−1,xt]+bi)i_{t}=\sigma\left(W_{i} \cdot\left[h_{t-1}, x_{t}\right]+b_{i}\right)it=σ(Wi⋅[ht−1,xt]+bi)
② 生成候选记忆：C~t=tanh⁡(WC⋅[ht−1,xt]+bC)\tilde{C}{t}=\tanh \left(W{C} \cdot\left[h_{t-1}, x_{t}\right]+b_{C}\right)C~t=tanh(WC⋅[ht−1,xt]+bC)（tanh输出-1~1，调节信息增减）

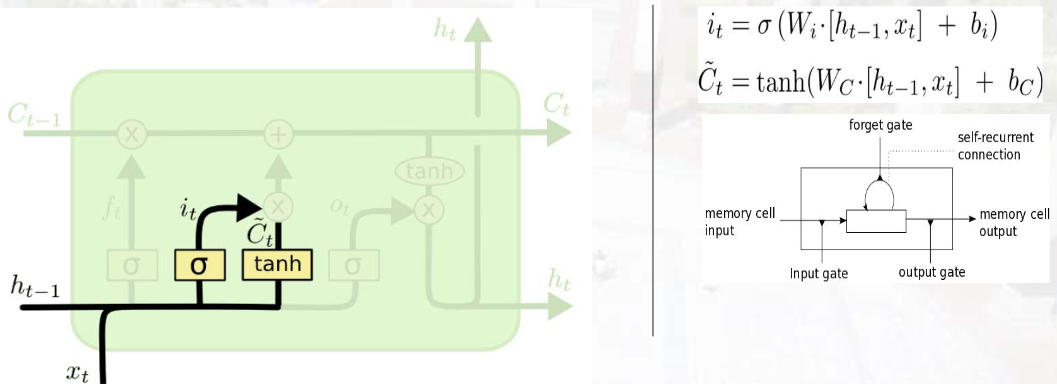
输入门计算，计算iti_tit查看短时记忆和当前输入的关系，用sigmoid映射到[0,1]，判断添加输入到长时记忆中。计算C^t\hat{C}_tC^t 计算一个此次要被添加的长时记忆值。tanh只是一个激活函数，和sigmoid作用不一样。

3. 记忆单元更新（Cell State Update）

作用：结合遗忘门和输入门，更新长期记忆。
计算：Ct=ft⊙Ct−1+it⊙C~tC_{t}=f_{t} \odot C_{t-1}+i_{t} \odot \tilde{C}{t}Ct=ft⊙Ct−1+it⊙C~t
其中，⊙\odot⊙ 为元素级乘法，Ct−1C{t-1}Ct−1 为上一时刻记忆单元，CtC_tCt 为当前时刻记忆单元。

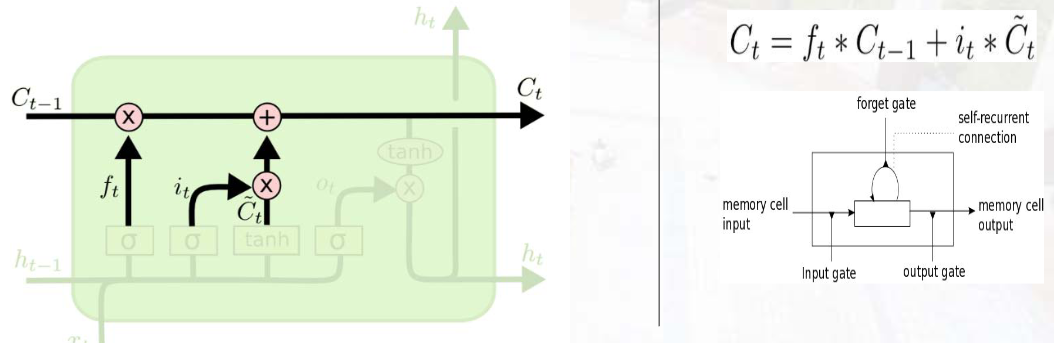
更新长时记忆。求出短时记忆被遗忘后的剩余，以及此次要被添加的输入，相加得到更新后的当前时刻的长时记忆。

4. 输出门（Output Gate）

作用：决定从记忆单元中输出哪些信息到隐藏状态。
计算：
① 筛选输出信息：ot=σ(Wo[ht−1,xt]+bo)o_{t}=\sigma\left(W_{o}\left[h_{t-1}, x_{t}\right]+b_{o}\right)ot=σ(Wo[ht−1,xt]+bo)
② 更新隐藏状态：ht=ot⊙tanh⁡(Ct)h_t = o_t \odot \tanh(C_t)ht=ot⊙tanh(Ct)（tanh将记忆单元值归一化到-1~1，再与输出门结果相乘）

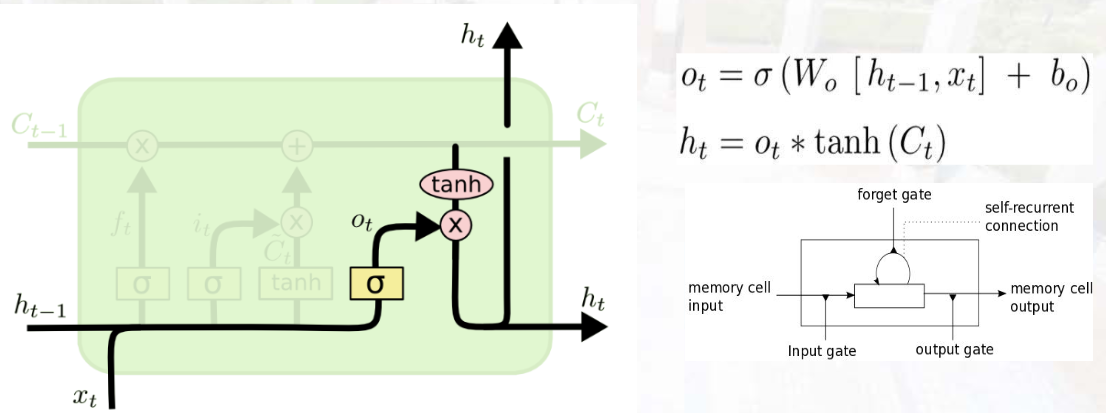
更新短时记忆。根据当前时刻的输入值，更新下一时刻的短时记忆。

激活函数作用

sigmoid：用于三门结构，输出0-1，模拟"门的开关"；
tanh：用于生成候选记忆和归一化记忆单元，输出-1~1，增强信息表达能力并维持数值稳定。

LSTM与GRU对比

门控循环单元（GRU）是LSTM的简化版，减少门数量和参数，计算效率更高：

对比维度	GRU（门控循环单元）	LSTM（长短期记忆网络）
门数量	2个（重置门、更新门）	3个（遗忘门、输入门、输出门）
记忆单元	无独立记忆单元（隐藏状态兼顾）	有独立记忆单元（Cell State）
参数数量	更少（计算更快）	更多（建模能力更强）
长序列处理能力	较好	更优（尤其长程依赖）

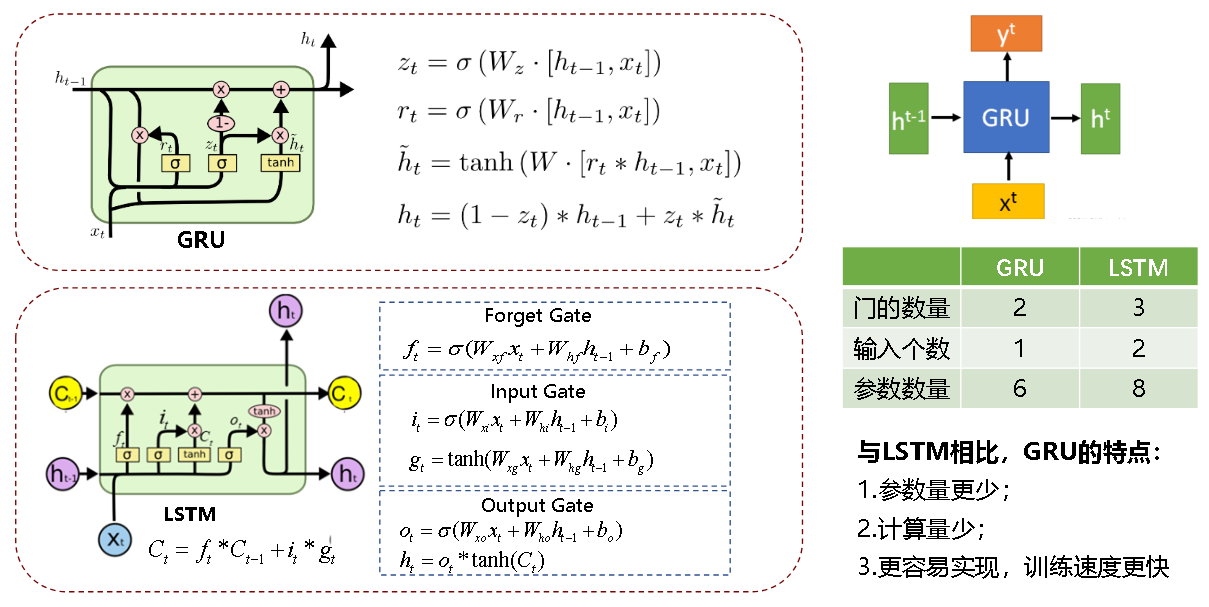
GRU讲解

在 GRU（门控循环单元）中，重置门（Reset Gate） 和 更新门（Update Gate） 是实现"记忆管理"的核心组件------通过简单的结构替代了 LSTM 的三大门控，却能高效平衡"短期依赖捕捉"与"长期记忆保留"，下面结合你的描述拆解两者的逻辑：

一、重置门（Reset Gate）："遗忘机制"------筛选要丢弃的过去信息

1. 核心作用：判断"过去信息中哪些该丢"

重置门的本质是对"上一时刻的隐藏状态 ht−1h_{t-1}ht−1（过去记忆）"做"筛选丢弃"：它会生成一个 [0,1] 区间的门控向量，向量中每个元素的数值大小，决定了"过去记忆对应位置的信息是否该被保留"。

若重置门某位置值 接近 0 ：表示"该位置的过去信息几乎全部丢弃"，此时模型更依赖"当前输入 xtx_txt"生成新信息，适合捕捉序列中的短期依赖（比如句子中相邻词的关联、时间序列的近期波动）；
若重置门某位置值 接近 1：表示"该位置的过去信息大部分保留"，模型会结合更多历史记忆生成新信息。

2. 计算逻辑（附公式）

重置门 rtr_trt 的计算需结合"当前输入 xtx_txt"和"上一时刻隐藏状态 ht−1h_{t-1}ht−1"，通过 sigmoid 激活映射到 [0,1] 区间：
rt=σ(Wxrxt+Whrht−1+br) r_t = \sigma\left( W_{xr} x_t + W_{hr} h_{t-1} + b_r \right) rt=σ(Wxrxt+Whrht−1+br)

Wxr、WhrW_{xr}、W_{hr}Wxr、Whr 是权重矩阵，brb_rbr 是偏置项，用于学习"输入与过去记忆的关联模式"；
σ\sigmaσ（sigmoid）是关键：确保输出在 [0,1] 区间，直接对应"信息保留/丢弃的比例"。

3. 对记忆的影响：参与生成"候选隐藏状态"

重置门的筛选结果，会直接作用于"候选隐藏状态 h~t\tilde{h}th~t"的计算（h~t\tilde{h}th~t 是"当前输入与筛选后过去记忆融合的新信息"）：
h~t=tanh⁡(Wxhxt+Whh(rt⊙ht−1)+bh) \tilde{h}t = \tanh\left( W{xh} x_t + W{hh} (r_t \odot h{t-1}) + b_h \right) h~t=tanh(Wxhxt+Whh(rt⊙ht−1)+bh)

其中 rt⊙ht−1r_t \odot h_{t-1}rt⊙ht−1 是元素级乘法 ------重置门 rtr_trt 像"过滤器"，逐元素控制 ht−1h_{t-1}ht−1 中信息的流入量：rtr_trt 越小，流入 h~t\tilde{h}_th~t 的过去信息越少，模型对"近期输入"的响应越敏感。

二、更新门（Update Gate）："关注机制"------决定要记住的过去信息

1. 核心作用：判断"过去信息中哪些该留，以及如何结合新信息"

更新门是 GRU 的"核心管理者"，它同时负责两件事：

保留过去记忆 ：决定"上一时刻隐藏状态 ht−1h_{t-1}ht−1 中有多少信息要传递到当前时刻 hth_tht"；
融入新信息 ：决定"候选隐藏状态 h~t\tilde{h}_th~t（当前新信息）中有多少要加入到当前时刻 hth_tht"。
这种"双向控制"让更新门能高效捕捉长期依赖（比如句子的主题、时间序列的整体趋势）：
若更新门某位置值 接近 1：表示"该位置的过去记忆几乎全部保留"，新信息融入少，适合传递长期稳定的记忆；
若更新门某位置值 接近 0：表示"该位置的过去记忆几乎全部替换为新信息"，适合响应序列中的新变化。

2. 计算逻辑（附公式）

更新门 ztz_tzt 的计算与重置门类似，同样通过 sigmoid 映射到 [0,1] 区间：
zt=σ(Wxzxt+Whzht−1+bz) z_t = \sigma\left( W_{xz} x_t + W_{hz} h_{t-1} + b_z \right) zt=σ(Wxzxt+Whzht−1+bz)

Wxz、WhzW_{xz}、W_{hz}Wxz、Whz 是权重矩阵，bzb_zbz 是偏置项，用于学习"长期记忆保留与新信息融入的平衡模式"。

3. 对记忆的影响：生成"最终隐藏状态"

更新门通过"加权融合"生成当前时刻的隐藏状态 hth_tht，公式如下：
ht=(1−zt)⊙h~t+zt⊙ht−1 h_t = (1 - z_t) \odot \tilde{h}t + z_t \odot h{t-1} ht=(1−zt)⊙h~t+zt⊙ht−1

zt⊙ht−1z_t \odot h_{t-1}zt⊙ht−1：保留的"过去记忆部分"------更新门值越大，保留的过去信息越多；
(1−zt)⊙h~t(1 - z_t) \odot \tilde{h}_t(1−zt)⊙h~t：融入的"新信息部分"------更新门值越小，融入的新信息越多；
两者相加后，hth_tht 既包含了筛选后的过去记忆，也融入了当前新信息，实现"记忆的动态更新"。

三、重置门 vs 更新门：核心差异与协同作用

维度	重置门（Reset Gate）rtr_trt	更新门（Update Gate）ztz_tzt
核心功能	筛选"要丢弃的过去信息"（遗忘机制）	平衡"保留的过去信息"与"融入的新信息"（关注机制）
作用对象	仅作用于"候选隐藏状态 h~t\tilde{h}_th~t"的计算	直接作用于"最终隐藏状态 hth_tht"的生成
依赖捕捉优势	擅长捕捉短期依赖（近期输入关联）	擅长捕捉长期依赖（长期记忆传递）
数值含义	值越小 → 丢弃的过去信息越多	值越大 → 保留的过去信息越多

05 序列到序列模型（Seq2Seq）

核心框架：编码器-解码器（Encoder-Decoder）

将序列处理分为"编码"和"解码"两步，解决输入输出序列长度不一致的问题（如机器翻译、文本摘要）。

1. 编码器（Encoder）

作用：将输入序列（如法语句子）编码为固定长度的"上下文向量（Context Vector, C）"，捕捉序列全局信息。
结构：通常由RNN/LSTM/Transformer编码器构成，将最后一个时间步的隐藏状态作为上下文向量 CCC。

2. 解码器（Decoder）

作用：根据上下文向量 CCC 和上一时刻输出，生成目标序列（如英语句子）。
结构：通常由RNN/LSTM/Transformer解码器构成，初始隐藏状态为 CCC，每个时间步生成一个输出（如单词），直到生成"结束标记（EOS）"。

关键符号

BOS（Begin-of-Sentence）：句子开始标记（如翻译任务中，解码器输入以BOS开头）；
EOS（End-of-Sentence）：句子结束标记（解码器生成EOS时停止输出）。

示例：机器翻译

输入（法语）："Je suis etudiant"（我是学生）→ 编码器编码为 CCC → 解码器生成输出（英语）："I am a student"（以BOS开头，EOS结尾）。

06 注意力机制（Attention）

核心问题：Seq2Seq的局限性

Seq2Seq中，编码器仅用一个固定长度的上下文向量 CCC 传递信息，当输入序列较长时，易丢失早期细节（如长句翻译中，前面的单词信息被稀释）。

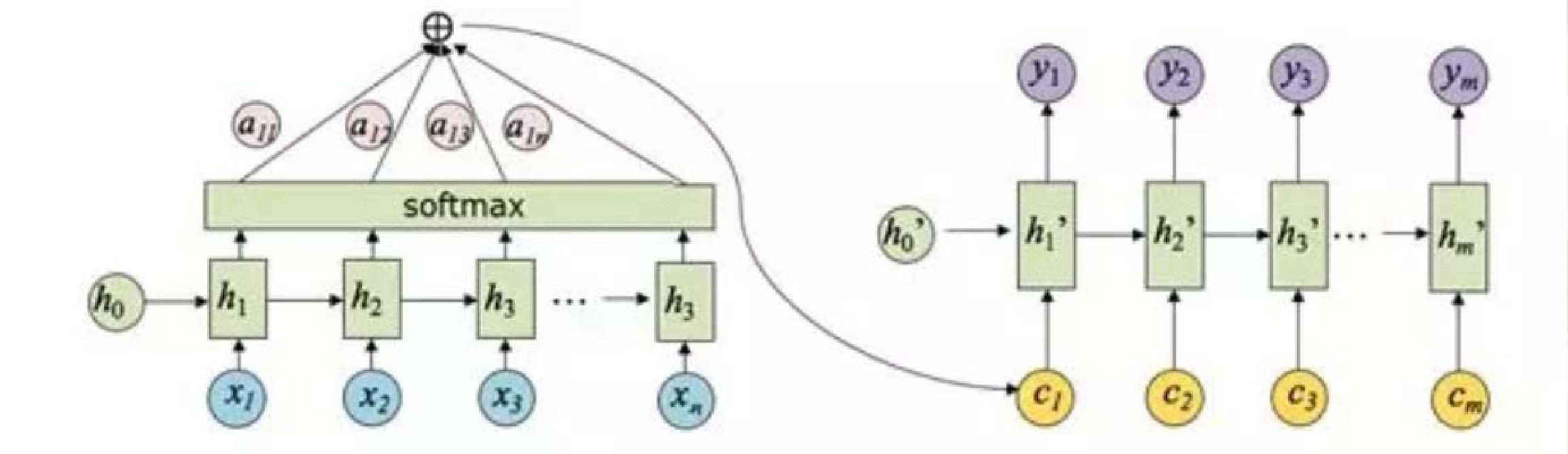
核心思想：动态上下文向量

decoder每个时间步生成输出时，"关注"编码器输入序列中与当前输出相关的部分，生成动态上下文向量 cic_ici （而非固定 CCC），提升长序列建模能力。

关键公式

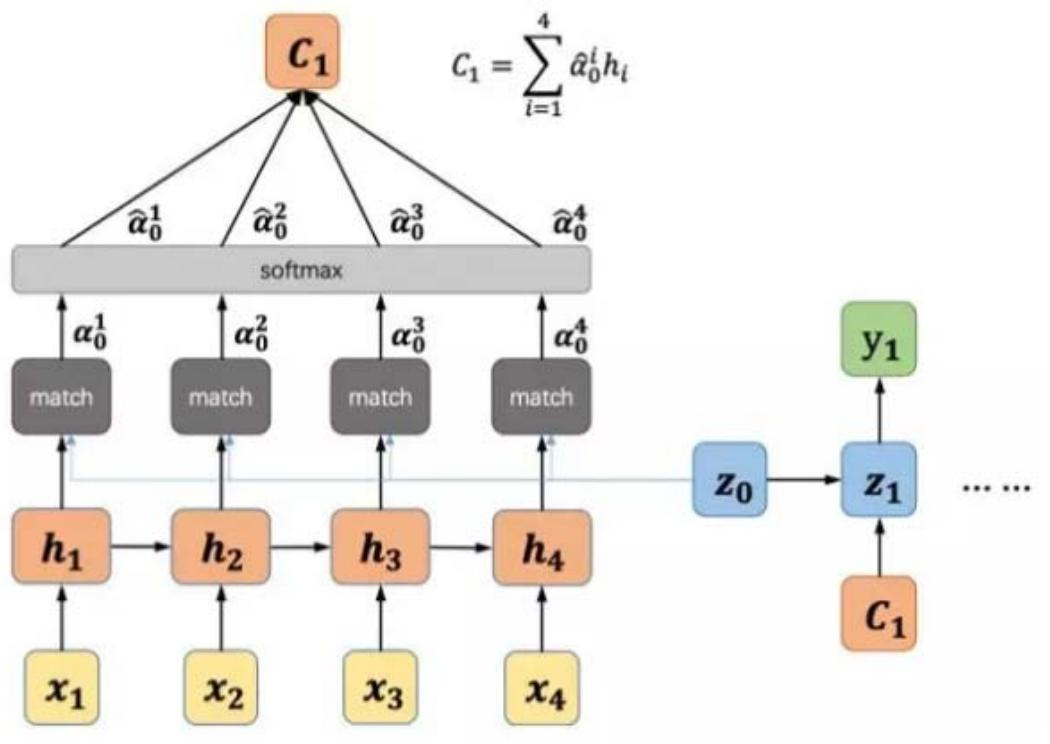
注意力权重计算 ：

① 计算匹配度（相似度）：eij=a(si−1,hj)e_{ij} = a(s_{i-1}, h_j)eij=a(si−1,hj)，其中 si−1s_{i-1}si−1 为解码器 i−1i-1i−1 时刻隐藏状态，hjh_jhj 为编码器 jjj 时刻隐藏状态，a(⋅)a(\cdot)a(⋅) 为相似度函数（如点积、余弦相似度）；

② 归一化权重：αij=exp⁡(eij)∑k=1Txexp⁡(eik)\alpha_{ij}=\frac{\exp \left(e_{ij}\right)}{\sum_{k=1}^{T_x} \exp \left(e_{ik}\right)}αij=∑k=1Txexp(eik)exp(eij)（Softmax归一化，αij\alpha_{ij}αij 表示解码器第 iii 步对编码器第 jjj 步的注意力权重）。
动态上下文向量 ：
ci=∑j=1Txαijhjc_i=\sum_{j=1}^{T_x} \alpha_{ij} h_jci=∑j=1Txαijhj（对编码器隐藏状态按注意力权重加权求和，聚焦相关信息）。
解码器输出 ：
p(yi∣y1,...,yi−1,x)=g(yi−1,si,ci)p\left(y_i | y_1, ..., y_{i-1}, x\right)=g\left(y_{i-1}, s_i, c_i\right)p(yi∣y1,...,yi−1,x)=g(yi−1,si,ci)

其中，g(⋅)g(\cdot)g(⋅) 为输出函数（如Softmax），yi−1y_{i-1}yi−1 为解码器上一时刻输出，sis_isi 为解码器当前隐藏状态。

07 Transformer模型（2017）

核心突破：完全基于注意力机制

摒弃RNN的循环结构，完全依赖自注意力（Self-Attention） 机制捕捉序列全局依赖，支持并行计算（RNN需按时间步串行计算），大幅提升训练效率。

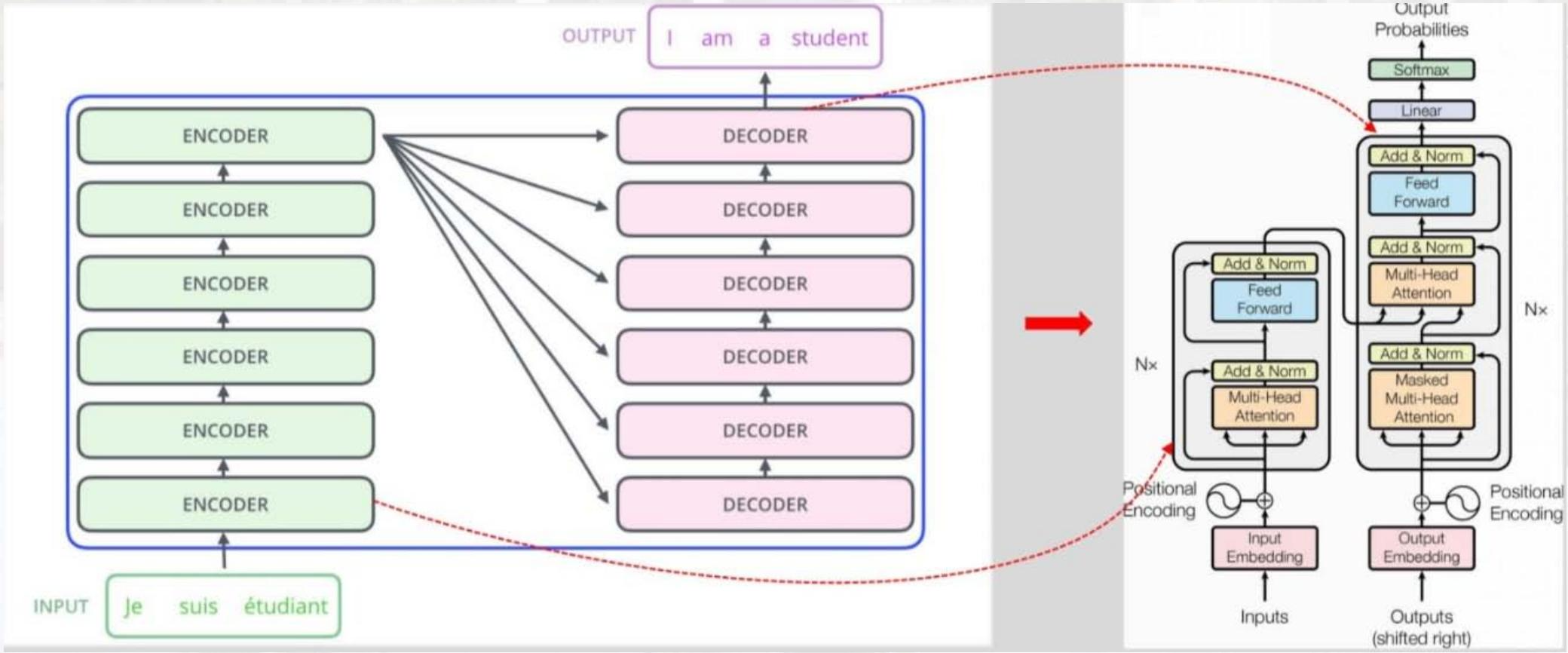
关键结构：编码器与解码器

1. 编码器（Encoder）

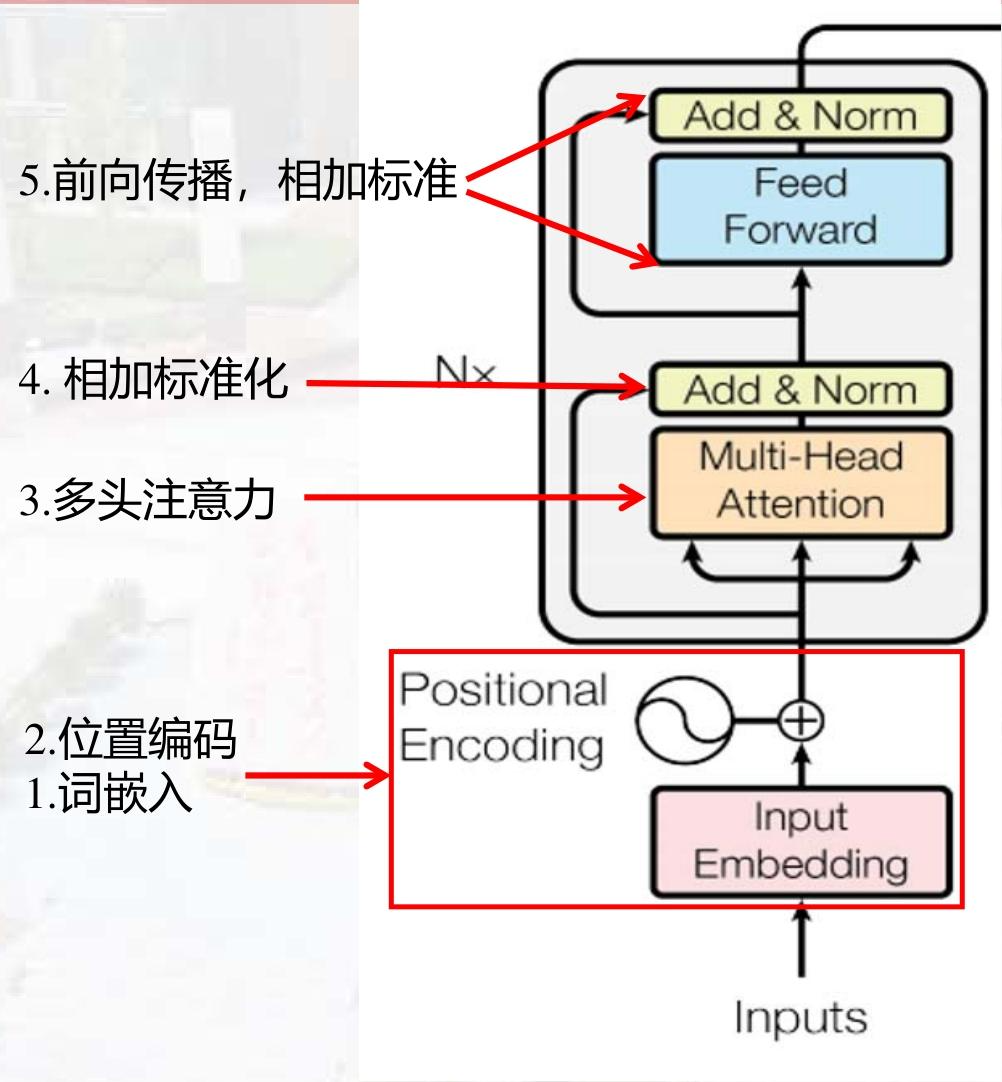
输入处理 ：

① 词嵌入（Token Embedding）：将单词映射为向量；

② 位置编码（Positional Encoding）：加入位置信息（因自注意力无时间顺序，需显式编码位置），公式为：
PE(pos,2i)=sin⁡(pos/100002i/dmodel)PE_{(pos, 2i)}=\sin \left(pos / 10000^{2i/d_{model}}\right)PE(pos,2i)=sin(pos/100002i/dmodel)
PE(pos,2i+1)=cos⁡(pos/100002i/dmodel)PE_{(pos, 2i+1)}=\cos \left(pos / 10000^{2i/d_{model}}\right)PE(pos,2i+1)=cos(pos/100002i/dmodel)

其中，pospospos 为位置，iii 为向量维度索引，dmodeld_{model}dmodel 为词嵌入维度。
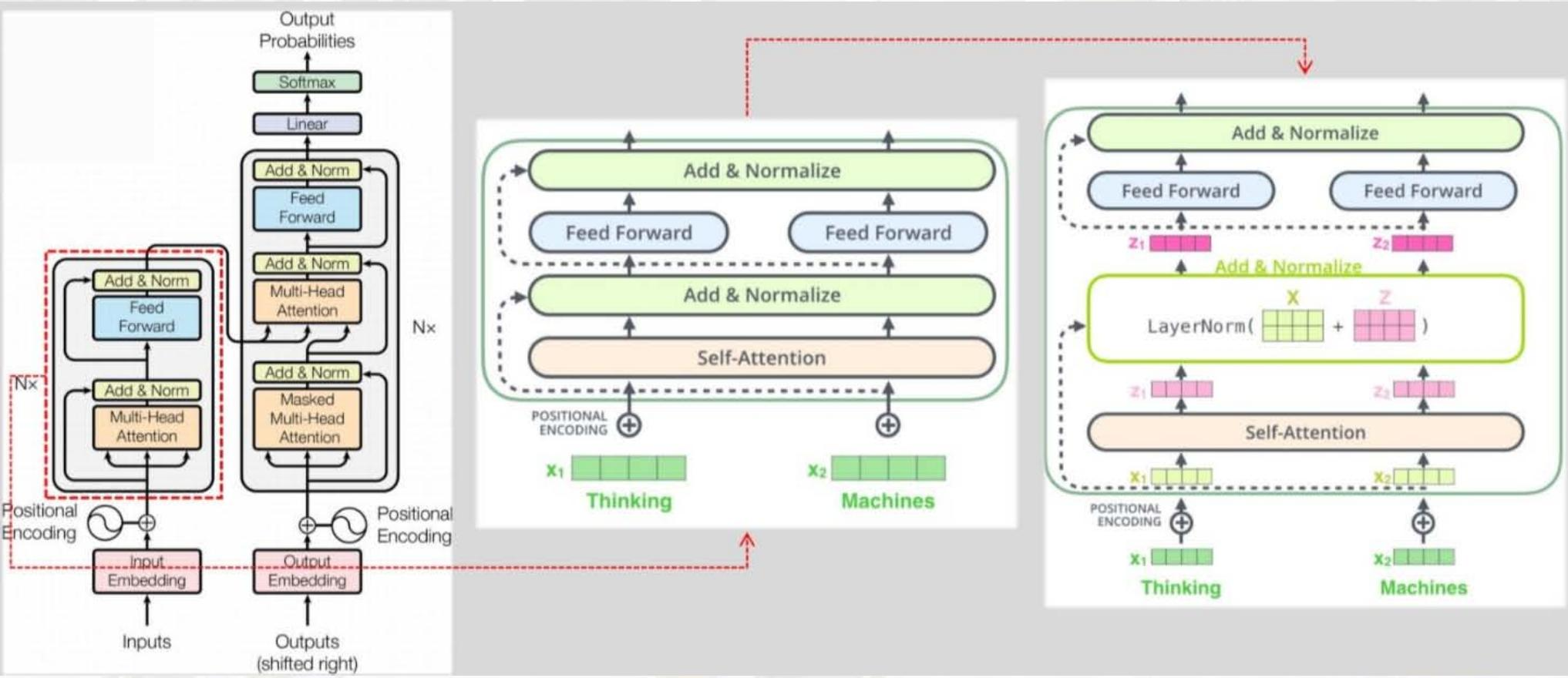
编码器块（重复N次） ：

① 多头自注意力（Multi-Head Self-Attention）：将自注意力拆分为多个"头"，并行捕捉不同类型的依赖（如语法依赖、语义依赖）；

② 前馈网络（Feed-Forward Network, FFN）：对每个位置的向量独立进行线性变换，公式为：
FFN(x)=max⁡(0,xW1+b1)W2+b2FFN(x) = \max \left(0, x W_1 + b_1\right) W_2 + b_2FFN(x)=max(0,xW1+b1)W2+b2（ReLU激活）；

③ 残差连接与层归一化（Add & Norm）：缓解梯度消失，加速训练。

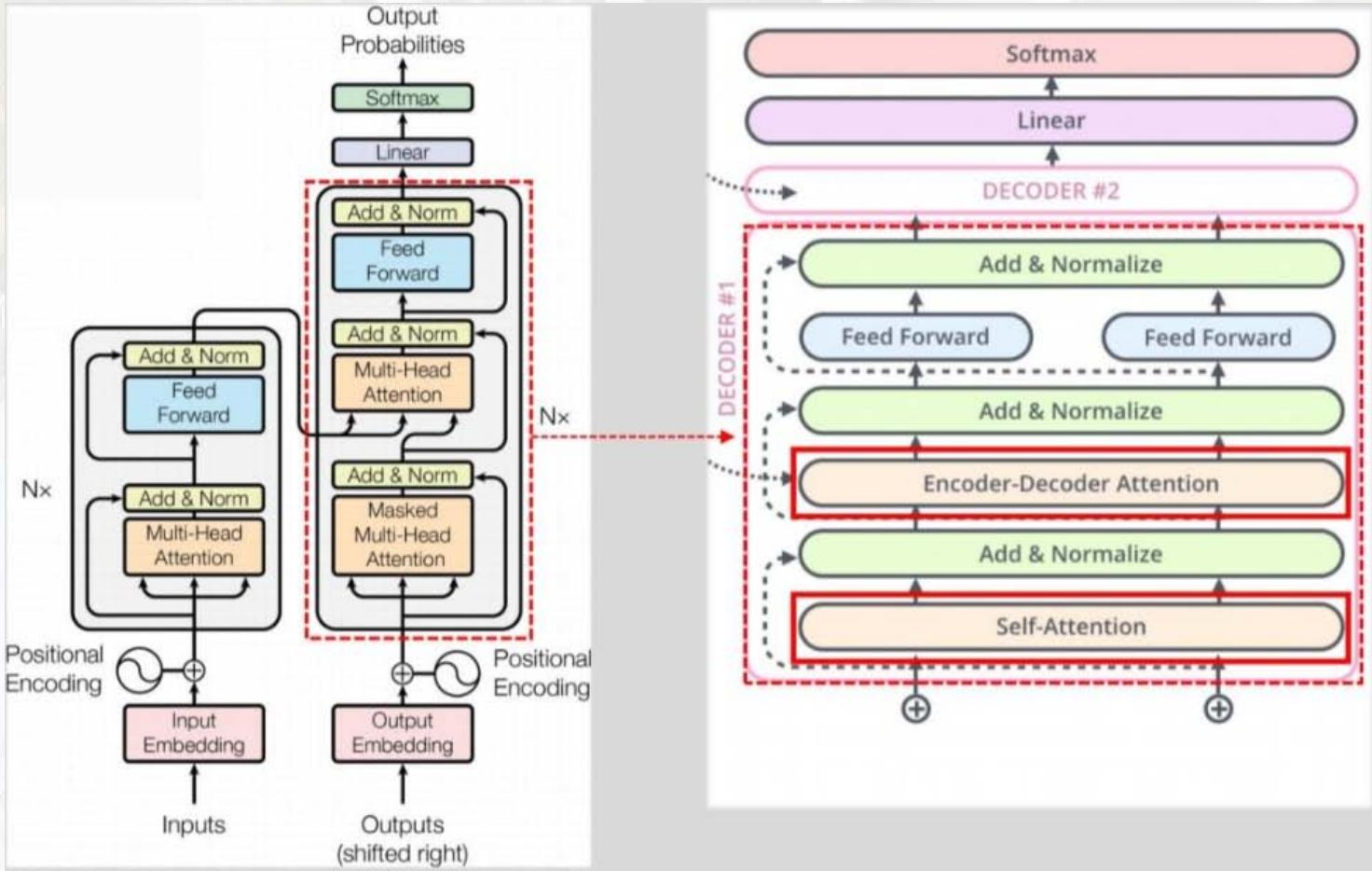
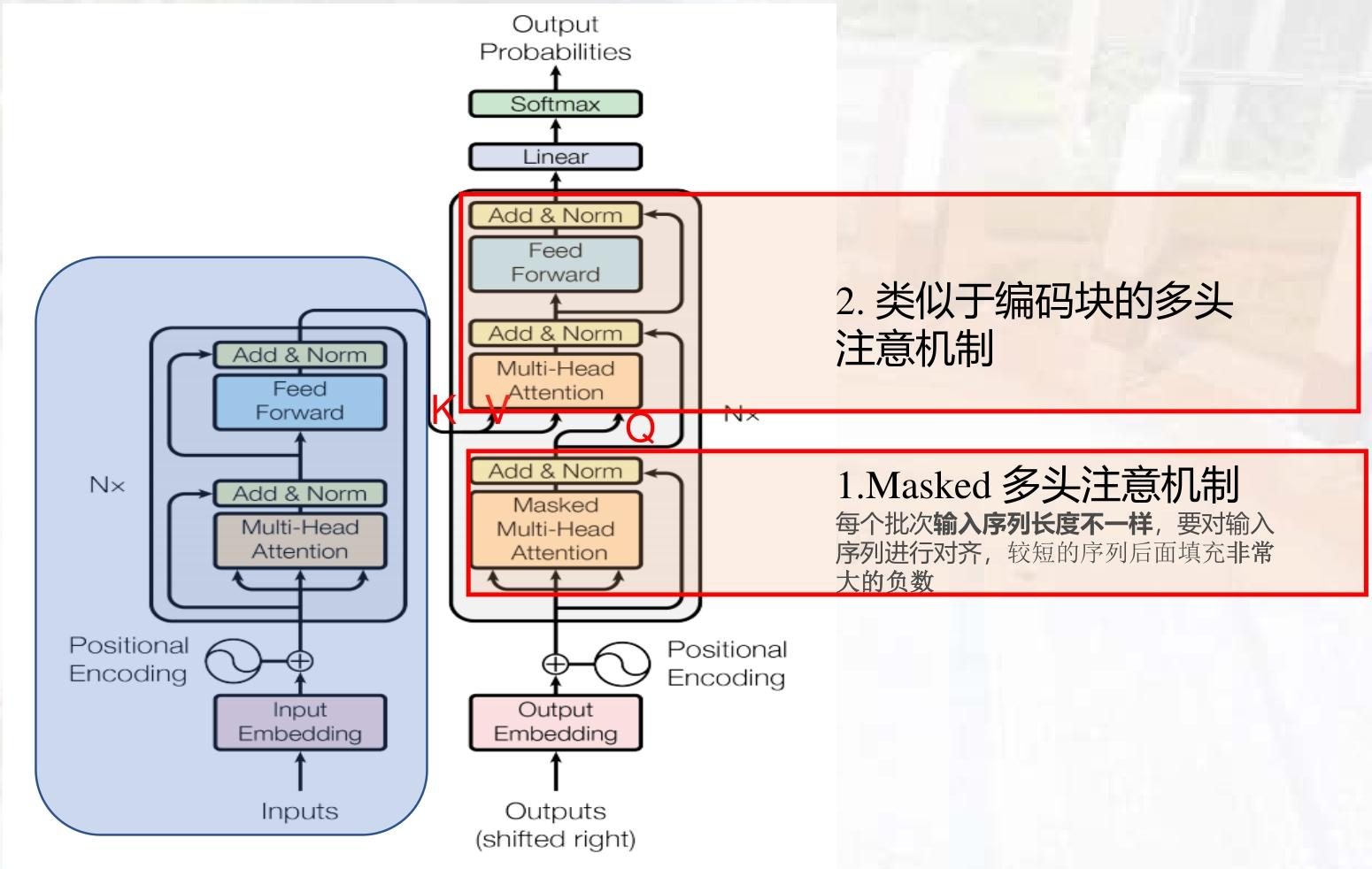
2. 解码器（Decoder）

额外结构 ：
① 掩码多头自注意力（Masked Multi-Head Self-Attention）：防止解码器"看到"未来时刻的输出（如生成第 iii 个单词时，仅能利用前 i−1i-1i−1 个单词）；
② 编码器-解码器注意力（Encoder-Decoder Attention）：解码器关注编码器输出的相关信息（类似Seq2Seq的注意力机制）。

自注意力机制（Self-Attention）

1. 核心概念：Q、K、V

查询（Query, Q）：当前位置的向量，用于"查询"其他位置的相关性；
键（Key, K）：其他位置的向量，用于"匹配"查询；
值（Value, V）：其他位置的向量，用于"生成"注意力输出。

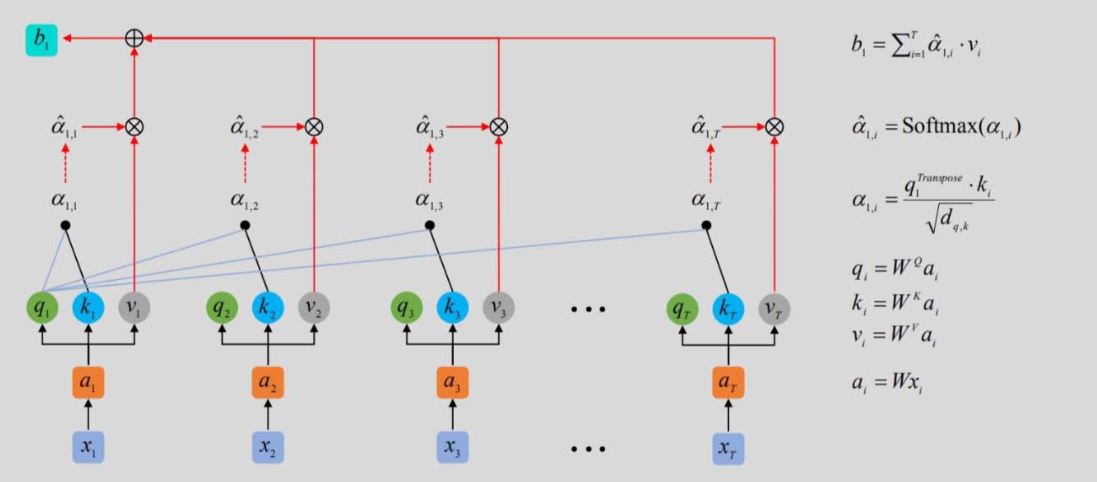
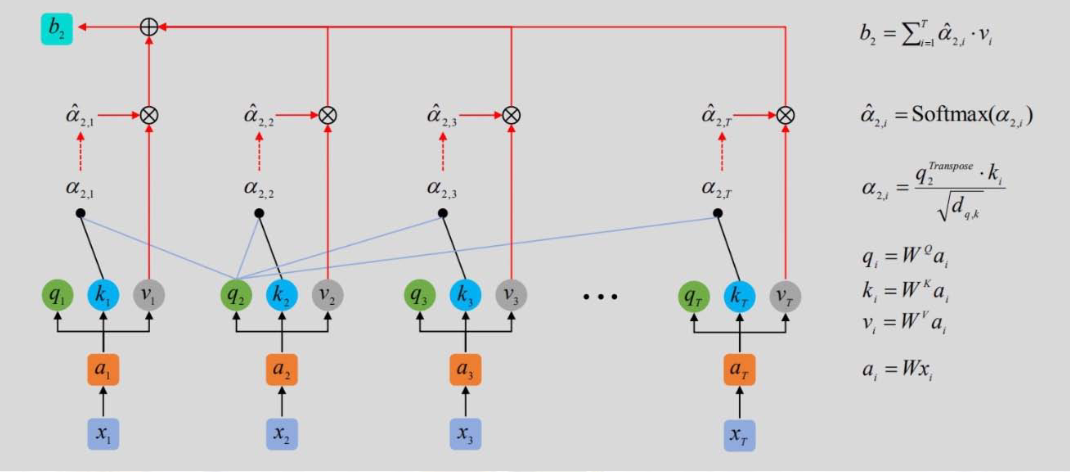
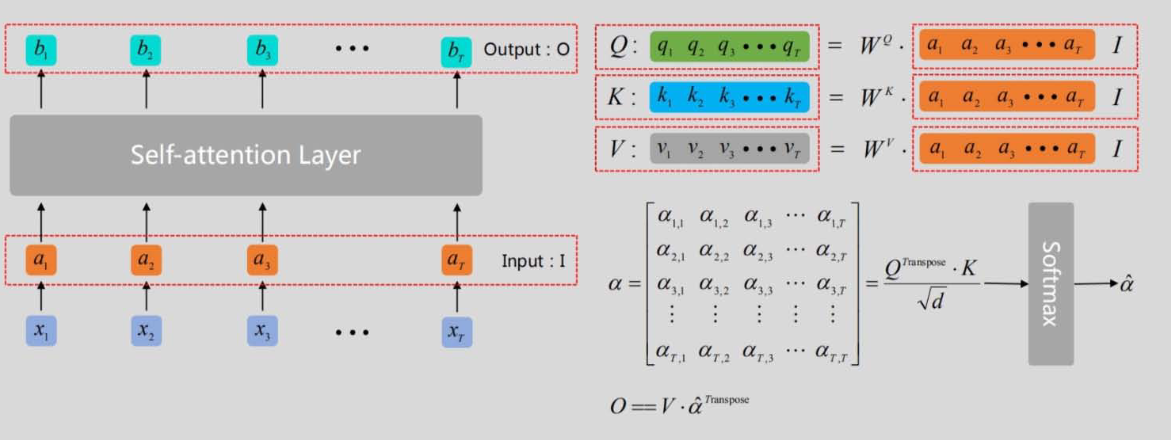
2. 计算步骤

线性变换：Q=XWQQ = X W_QQ=XWQ，K=XWKK = X W_KK=XWK，V=XWVV = X W_VV=XWV（WQ、WK、WVW_Q、W_K、W_VWQ、WK、WV 为可训练权重）；
计算相似度：scores=QKTdk\text{scores} = \frac{Q K^T}{\sqrt{d_k}}scores=dk QKT（dk\sqrt{d_k}dk 为缩放因子，避免维度过高导致Softmax梯度消失，dkd_kdk 为Q/K的维度）；
掩码（可选）：对解码器，掩盖未来位置的得分（设为-∞）；
归一化：α=Softmax(scores)\alpha = \text{Softmax}(\text{scores})α=Softmax(scores)（注意力权重）；
加权求和：Attention(Q,K,V)=αV\text{Attention}(Q,K,V) = \alpha VAttention(Q,K,V)=αV（自注意力输出）。

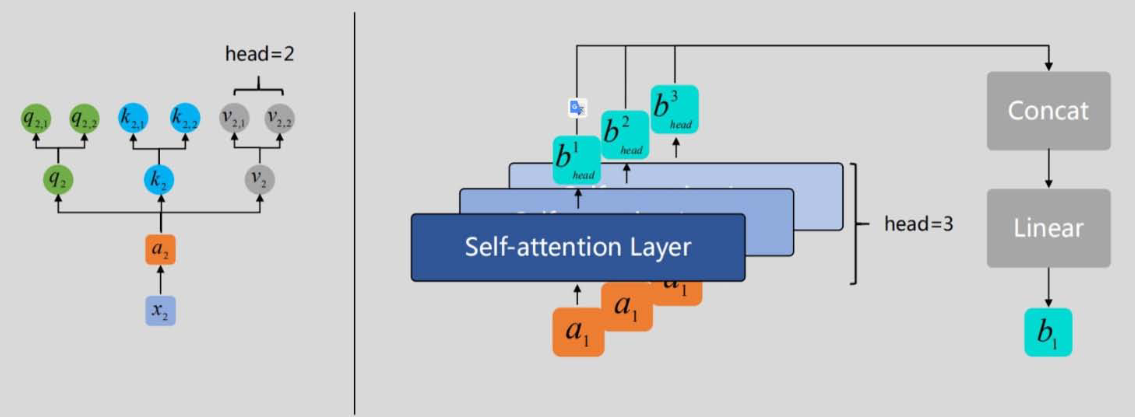
3. 多头自注意力（Multi-Head Attention）

将Q、K、V拆分为 hhh 个"头"，分别计算自注意力后拼接，再通过线性变换融合：
MultiHead(Q,K,V)=Concat(head1,head2,...,headh)WOMultiHead(Q,K,V) = \text{Concat}(head_1, head_2, ..., head_h) W_OMultiHead(Q,K,V)=Concat(head1,head2,...,headh)WO

其中，headi=Attention(QWQi,KWKi,VWVi)head_i = \text{Attention}(Q W_{Q_i}, K W_{K_i}, V W_{V_i})headi=Attention(QWQi,KWKi,VWVi)，WOW_OWO 为融合权重。

08 BERT模型（2018）

核心定位：基于Transformer的预训练语言模型

通过"预训练+微调"模式，在海量文本上预训练通用语言表示，再针对具体任务（如情感分类、问答）微调，大幅提升NLP任务性能。

模型结构

基础架构 ：仅使用Transformer编码器（无解码器），分为两种规模：

① BERT-BASE：12层Transformer编码器，768维隐藏层，12个自注意力头，1.1亿参数；

② BERT-LARGE：24层Transformer编码器，1024维隐藏层，16个自注意力头，3.4亿参数。
输入表示 ：

输入向量 = 词嵌入（Token Embedding） + 段落嵌入（Segment Embedding，区分两个句子） + 位置嵌入（Positional Embedding），示例：

输入文本："[CLS] my dog is cute [SEP] he likes play ##ing [SEP]"
- $CLS\]：分类标记，用于句子级任务（如情感分类），其输出作为句子表示；$
- ##ing：词片段标记（BERT使用WordPiece分词，将未登录词拆分为子词）。

预训练任务

通过两个无监督任务让模型学习语言规律：

1. 掩码语言模型（Masked Language Modeling, MLM）

任务：随机掩盖输入中15%的单词，让模型预测被掩盖的单词。
- 80%概率替换为[MASK]（如"my dog is [MASK]"）；
- 10%概率替换为随机单词（如"my dog is cat"）；
- 10%概率保留原单词（如"my dog is cute"）。
目的：让模型学习上下文依赖（如通过"my dog"预测"cute"）。

2. 下一句预测（Next Sentence Prediction, NSP）

任务：给定两个句子A和B，判断B是否为A的下一句（标签为"isNext"或"NotNext"）。
- 50%概率为真实下一句（如A："She cooked pasta"，B："It was delicious" → "isNext"）；
- 50%概率为随机句子（如A："She cooked pasta"，B："Birds fly in the sky" → "NotNext"）。
目的：让模型学习句子间的逻辑关系（如因果、转折）。

微调任务与性能

在GLUE（通用语言理解评估）任务集（含情感分类、文本蕴含、语义相似度等9个任务）上，BERT-LARGE模型的平均准确率达82.1%，超过传统模型（如BiLSTM+ELMo）；在SQuAD问答任务中，BERT-LARGE的F1分数达91.8%，接近人类水平（91.2%）。

09 视觉Transformer（ViT，Vision Transformer）

核心思想：将图像转化为序列，用Transformer处理

打破CNN在计算机视觉领域的垄断，将图像分割为"图像块（Patch）"，视为类似文本单词的序列，用Transformer编码器进行分类或回归。

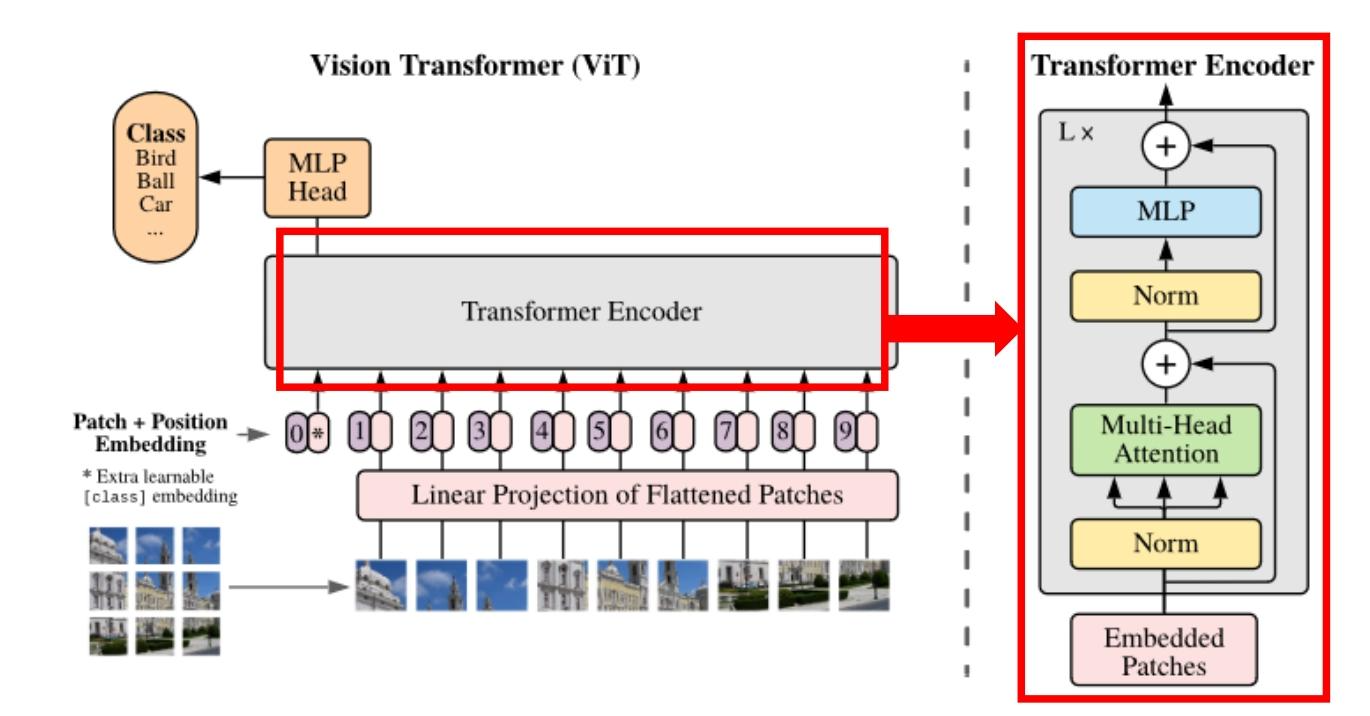
模型流程

1. 图像块分割与嵌入（Patch Embedding）

步骤：
① 将输入图像（如224×224×3，H×W×C）分割为大小为P×P的图像块（如P=16），共生成 N=H×WP×PN = \frac{H \times W}{P \times P}N=P×PH×W 个块（224×224图像分割为16×16块，得 N=196N=196N=196 个块）；
② 将每个图像块展平（如16×16×3=768维），通过线性投影映射到D维特征空间（如D=768），得到"图像块嵌入"（Patch Embedding）。

2. 加入类别标记与位置编码

类别标记（[class]）：类似BERT的[CLS]，在图像块嵌入序列前添加一个可学习的向量，其最终输出作为图像的全局表示，用于分类；
位置编码（Positional Embedding）：与Transformer类似，使用可学习的1D位置向量，与图像块嵌入相加（而非拼接），保留空间位置信息。

最终输入序列维度：(N+1)×D(N+1) \times D(N+1)×D（如196+1=197个向量，每个768维）。

3. Transformer编码器处理

结构：重复L层Transformer编码器块（与BERT编码器一致），每层包含：
① 多头自注意力（捕捉图像块间的空间依赖，如"猫的眼睛"与"猫的耳朵"的关联）；
② 前馈网络（FFN）；
③ 残差连接与层归一化。

4. 分类头（Classification Head）

取Transformer编码器输出的"类别标记（[class]）"向量，通过一个简单的MLP（或线性层）输出类别概率（如ImageNet的1000类）。

关键公式

输入序列构建 ：
z0=[xclass;xp1E;xp2E;⋯ ;xpNE]+Eposz_{0}=\left[x_{class} ; x_{p}^{1} E ; x_{p}^{2} E ; \cdots ; x_{p}^{N} E\right]+E_{pos}z0=[xclass;xp1E;xp2E;⋯;xpNE]+Epos

其中，xclassx_{class}xclass 为类别标记，xpix_p^ixpi 为第 iii 个图像块，EEE 为线性投影权重（R(P2⋅C)×D\mathbb{R}^{(P^2 \cdot C) \times D}R(P2⋅C)×D），EposE_{pos}Epos 为位置编码（R(N+1)×D\mathbb{R}^{(N+1) \times D}R(N+1)×D）。
编码器块更新 ：
zℓ′=MSA(LN(zℓ−1))+zℓ−1z_{\ell}' = \text{MSA}\left(\text{LN}(z_{\ell-1})\right) + z_{\ell-1}zℓ′=MSA(LN(zℓ−1))+zℓ−1（多头自注意力+残差连接）
zℓ=MLP(LN(zℓ′))+zℓ′z_{\ell} = \text{MLP}\left(\text{LN}(z_{\ell}')\right) + z_{\ell}'zℓ=MLP(LN(zℓ′))+zℓ′（前馈网络+残差连接）

其中，ℓ=1,2,...,L\ell=1,2,...,Lℓ=1,2,...,L 为编码器层数，zL0z_L^0zL0 为类别标记的最终输出。
分类输出 ：
y=LN(zL0)y = \text{LN}(z_L^0)y=LN(zL0)（类别标记输出经层归一化后，输入分类头）。

实验性能

预训练数据影响：ViT在小数据集（如ImageNet-1k，120万样本）上性能略逊于CNN（如ResNet），但在大数据集（如JFT-300M，3亿样本）上性能超越CNN，证明其"数据饥渴"特性；
图像分类结果：在ImageNet-21k（1400万样本）预训练后，ViT-L/16（大模型，16×16图像块）在ImageNet-1k上的Top-1准确率达85.9%，超过ResNet等传统CNN模型。

核心优势

并行计算：无CNN的卷积操作，图像块处理可完全并行，训练效率高；
全局依赖：自注意力机制可直接捕捉图像全局依赖（如CNN需通过多层卷积间接捕捉）；
跨模态迁移：与NLP的Transformer结构统一，便于跨模态任务（如图文生成）的模型设计。