【OPENGL ES 3.0 学习笔记】第十七天：模型矩阵、视图矩阵与投影矩阵

模型矩阵、视图矩阵与投影矩阵

在3D图形渲染中，将虚拟三维世界的顶点最终投射到二维屏幕上，需要经过三次关键的坐标变换：模型变换（Model Transformation） 、视图变换（View Transformation） 和投影变换（Projection Transformation）。

对应的三个矩阵------模型矩阵（Model Matrix） 、视图矩阵（View Matrix） 和投影矩阵（Projection Matrix）（合称MVP矩阵），是连接3D空间与2D屏幕的"数学桥梁"。

本文将从坐标变换的本质出发，详细拆解这三个矩阵的数学原理、构建方法与工程实践，揭示它们如何协同完成"3D顶点→2D像素"的精准映射。

从"局部"到"屏幕"的链路

在3D渲染流水线中，一个顶点从被定义到最终显示在屏幕上，需要经历5个坐标系 的转换。而模型、视图、投影矩阵正是这一转换链路的核心驱动者：

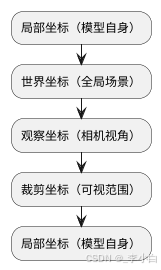
模型矩阵（M）：负责"局部坐标→世界坐标"的转换，决定模型在全局场景中的位置、姿态和大小；
视图矩阵（V）：负责"世界坐标→观察坐标"的转换，模拟相机的"视角"（位置和朝向）；
投影矩阵（P）：负责"观察坐标→裁剪坐标"的转换，定义相机的"可视范围"和"透视效果"。

这三个矩阵的组合（MVP = P×V×M）是3D渲染的"黄金公式"，所有3D引擎（如OpenGL、Unity、Unreal）的底层渲染逻辑都基于此。

模型矩阵（Model Matrix）

模型矩阵的核心作用是将模型的局部坐标（模型自身坐标系下的顶点）转换为世界坐标（全局场景坐标系下的顶点） 。它通过组合缩放（Scale） 、旋转（Rotation） 、平移（Translation） 三种基础变换，描述模型在世界中的大小、朝向和位置。

1. 局部坐标与世界坐标：为什么需要模型矩阵？

局部坐标 ：模型在自身坐标系下的顶点坐标，原点通常位于模型几何中心（如立方体的中心、人物的重心），与世界无关。例如，一个立方体的局部坐标可能是(-1,-1,-1)到(1,1,1)，无论它在世界中如何移动，这些坐标始终不变。
世界坐标：全局场景的统一坐标系，原点是场景的"中心"，所有模型的位置都通过世界坐标描述。例如，"玩家在(5,0,-3)，敌人在(10,0,2)"，通过世界坐标可确定模型间的相对位置。

模型矩阵的作用，就是将每个顶点的局部坐标"映射"到世界坐标，让分散的模型在全局场景中形成正确的空间关系。

2. 模型矩阵的组成：缩放→旋转→平移的组合

模型矩阵是缩放矩阵 、旋转矩阵 、平移矩阵 的乘积。由于矩阵乘法不满足交换律，变换顺序必须严格遵循"缩放→旋转→平移"（否则会导致非预期的扭曲，如平移后旋转会让模型绕世界原点而非自身中心旋转）。

（1）缩放矩阵（Scale Matrix）：调整模型大小

缩放矩阵用于沿x、y、z轴按比例放大或缩小模型，公式如下（顶点以齐次坐标(x,y,z,1)表示，矩阵为4×4以便与平移矩阵兼容）：

Mscale(sx,sy,sz)=[sx0000sy0000sz00001]M_{scale}(s_x, s_y, s_z) = \begin{bmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}Mscale(sx,sy,sz)= sx0000sy0000sz00001

s_x, s_y, s_z 分别为x、y、z轴的缩放因子（s=1表示不缩放，s>1放大，0<s<1缩小）；
示例：将局部坐标(1,2,3)沿x轴缩放2倍、y轴缩放0.5倍，结果为(2,1,3)：
[200000.50000100001]×[1231]=[2131]\begin{bmatrix}2&0&0&0\\0&0.5&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix} \times \begin{bmatrix}1\\2\\3\\1\end{bmatrix} = \begin{bmatrix}2\\1\\3\\1\end{bmatrix} 200000.50000100001 × 1231 = 2131

（2）旋转矩阵（Rotation Matrix）：调整模型朝向

旋转矩阵用于让模型绕坐标轴旋转指定角度（右手定则：四指沿旋转方向，拇指指向轴正方向），常见的三个旋转矩阵如下：

绕x轴旋转θ角 （y、z分量变化）：
MrotateX(θ)=[10000cos⁡θ−sin⁡θ00sin⁡θcos⁡θ00001]M_{rotateX}(θ) = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cosθ & -\sinθ & 0 \\ 0 & \sinθ & \cosθ & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}MrotateX(θ)= 10000cosθsinθ00−sinθcosθ00001
绕y轴旋转θ角 （x、z分量变化）：
MrotateY(θ)=[cos⁡θ0sin⁡θ00100−sin⁡θ0cos⁡θ00001]M_{rotateY}(θ) = \begin{bmatrix} \cosθ & 0 & \sinθ & 0 \\ 0 & 1 & 0 & 0 \\ -\sinθ & 0 & \cosθ & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}MrotateY(θ)= cosθ0−sinθ00100sinθ0cosθ00001
绕z轴旋转θ角 （x、y分量变化）：
MrotateZ(θ)=[cos⁡θ−sin⁡θ00sin⁡θcos⁡θ0000100001]M_{rotateZ}(θ) = \begin{bmatrix} \cosθ & -\sinθ & 0 & 0 \\ \sinθ & \cosθ & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}MrotateZ(θ)= cosθsinθ00−sinθcosθ0000100001
示例：将顶点(1,0,0)绕z轴旋转90°（θ=π/2，cosθ=0，sinθ=1），结果为(0,1,0)：

**[0−100100000100001]×[1001]=[0101]∗∗\begin{bmatrix}0&-1&0&0\\1&0&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix} \times \begin{bmatrix}1\\0\\0\\1\end{bmatrix} = \begin{bmatrix}0\\1\\0\\1\end{bmatrix}** 0100−100000100001 × 1001 = 0101 ∗∗
复合旋转：若需绕多个轴旋转（如先绕x轴再绕y轴），需将对应旋转矩阵相乘（M = M_{rotateY} × M_{rotateX}），顺序不同结果不同（通常遵循"Z-X-Y"或"Y-X-Z"顺序，避免万向锁问题）。

（3）平移矩阵（Translation Matrix）：调整模型位置

平移矩阵用于将模型沿x、y、z轴移动指定距离，公式如下：

Mtranslate(tx,ty,tz)=[100tx010ty001tz0001]M_{translate}(t_x, t_y, t_z) = \begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}Mtranslate(tx,ty,tz)= 100001000010txtytz1

t_x, t_y, t_z 分别为x、y、z轴的平移距离；
示例：将顶点(1,2,3)沿x轴平移5、z轴平移-2，结果为(6,2,1)：
[10050100001−20001]×[1231]=[6211]\begin{bmatrix}1&0&0&5\\0&1&0&0\\0&0&1&-2\\0&0&0&1\end{bmatrix} \times \begin{bmatrix}1\\2\\3\\1\end{bmatrix} = \begin{bmatrix}6\\2\\1\\1\end{bmatrix} 10000100001050−21 × 1231 = 6211

（4）模型矩阵的组合：严格遵循"缩放→旋转→平移"

模型矩阵的完整构建公式为：
M = M_{translate} × M_{rotate} × M_{scale}

计算逻辑：顶点先经过缩放，再旋转，最后平移（矩阵乘法从右向左执行）；

示例：一个模型先沿各轴缩放0.5倍，再绕y轴旋转90°，最后平移到(10,0,5)，其模型矩阵为：

java 复制代码

// 伪代码：使用GLM库构建模型矩阵
glm::mat4 model = glm::mat4(1.0f); // 单位矩阵（初始状态）
model = glm::translate(model, glm::vec3(10, 0, 5)); // 平移（最后执行）
model = model * glm::rotate(glm::radians(90.0f), glm::vec3(0, 1, 0)); // 旋转（中间执行）
model = model * glm::scale(glm::vec3(0.5f, 0.5f, 0.5f)); // 缩放（最先执行）

3. 模型矩阵的工程意义：让场景"活"起来

静态模型：模型矩阵固定（如地面、建筑）；
动态模型：通过实时更新模型矩阵实现动画（如人物移动、物体旋转）；
实例化渲染：多个相同模型（如树木、敌人）可通过不同模型矩阵实现"一模多态"，大幅提升渲染效率。

视图矩阵（View Matrix）

视图矩阵的核心作用是将世界坐标转换为观察坐标（以相机为中心的坐标）。

它本质是"将相机移动到世界原点，并调整朝向为默认方向（沿-z轴）"的逆变换------因为在3D渲染中，我们通常不"移动相机"，而是通过"移动整个世界"来模拟相机视角的变化。

1. 观察坐标：以相机为中心的"主观视角"

观察坐标系的原点是相机的位置，z轴负方向为相机的"视线方向"（OpenGL默认），x轴向右，y轴向上。在观察坐标中：

相机前方的物体z值为负（在视线方向上）；
相机后方的物体z值为正（会被后续裁剪剔除）；
所有顶点的坐标都表示"相对于相机的位置"。

2. 相机参数：定义视图矩阵的三要素

构建视图矩阵需要三个关键参数（相机的"三要素"）：

eye：相机在世界坐标系中的位置（(x_e, y_e, z_e)）；
center：相机的目标点（看向的位置，(x_c, y_c, z_c)）；
up：相机的上方向向量（通常为(0,1,0)，即"头顶朝上"）。

基于这三个参数，视图矩阵的构建分为两步：相机旋转 （调整朝向）和相机平移（移动到原点）。

3. 视图矩阵的数学构建：旋转+平移的逆变换

（1）第一步：计算相机的三个正交轴

首先根据相机参数计算观察坐标系的三个正交轴（确保x、y、z轴两两垂直）：

视线方向（z轴） ：z_axis = normalize(eye - center)（指向相机后方，与视线方向相反）；
水平右方向（x轴） ：x_axis = normalize(cross(up, z_axis))（与视线方向垂直）；
垂直上方向（y轴） ：y_axis = cross(z_axis, x_axis)（确保与x、z轴正交）。

（normalize为归一化函数，cross为叉积运算）

（2）第二步：构建视图矩阵

视图矩阵是"旋转矩阵"与"平移矩阵"的乘积，公式如下：

mathV=[xaxis.xyaxis.xzaxis.x−dot(xaxis,eye)xaxis.yyaxis.yzaxis.y−dot(yaxis,eye)xaxis.zyaxis.zzaxis.z−dot(zaxis,eye)0001]math V = \begin{bmatrix} x_axis.x & y_axis.x & z_axis.x & -dot(x_axis, eye) \\ x_axis.y & y_axis.y & z_axis.y & -dot(y_axis, eye) \\ x_axis.z & y_axis.z & z_axis.z & -dot(z_axis, eye) \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}mathV= xaxis.xxaxis.yxaxis.z0yaxis.xyaxis.yyaxis.z0zaxis.xzaxis.yzaxis.z0−dot(xaxis,eye)−dot(yaxis,eye)−dot(zaxis,eye)1

前3列是旋转矩阵：将世界坐标系旋转至与相机朝向一致；
第4列是平移矩阵：-dot(x_axis, eye)等表示将相机位置平移到原点（抵消相机的世界坐标）；
dot为点积运算，用于计算平移距离。

4. 工程实践：用库函数快速构建视图矩阵

实际开发中无需手动计算矩阵，可使用图形库（如GLM、Unity的Matrix4x4.LookAt）直接构建：

java 复制代码

// GLM库示例：构建视图矩阵
glm::vec3 eye(0.0f, 2.0f, 5.0f);    // 相机位置：(0,2,5)
glm::vec3 center(0.0f, 0.0f, 0.0f); // 目标点：原点
glm::vec3 up(0.0f, 1.0f, 0.0f);     // 上方向：y轴
glm::mat4 view = glm::lookAt(eye, center, up); // 直接生成视图矩阵

效果：所有世界坐标的顶点会被"转换"为以eye为原点、朝向center的观察坐标。

投影矩阵（Projection Matrix）：定义相机的"可视范围"

投影矩阵的核心作用是将观察坐标转换为裁剪坐标，它定义了相机的"可视范围"（裁剪体）和"投影方式"（透视或正交），是实现"近大远小"等3D视觉效果的关键。

1. 裁剪坐标与NDC：投影矩阵的输出目标

裁剪坐标 ：投影矩阵的输出，是齐次坐标(x,y,z,w)，需满足-w ≤ x ≤ w、-w ≤ y ≤ w、-w ≤ z ≤ w（超出范围的顶点会被裁剪）；
规范化设备坐标（NDC） ：裁剪坐标经"透视除法"（x/w, y/w, z/w）后得到，范围固定为[-1,1]×[-1,1]×[-1,1]，是设备无关的标准化坐标。

投影矩阵的本质是"将观察坐标中的可视区域"映射到NDC范围。

2. 透视投影矩阵（Perspective Projection）：模拟人眼视觉

透视投影会产生"近大远小"的效果（符合人眼视觉），适用于3D游戏、AR/VR等场景。其裁剪体是一个"视锥体"（frustum），由近裁剪面、远裁剪面和四个侧面组成。

（1）透视投影的参数

构建透视投影矩阵需要四个参数：

fov：垂直视场角（如60°，视野越广，能看到的范围越大）；
aspect：屏幕宽高比（width/height，避免画面拉伸）；
near：近裁剪面距离（相机前方最近可视距离，必须>0）；
far：远裁剪面距离（相机前方最远可视距离）。

（2）透视投影矩阵的公式

Ppersp=[1tan⁡(fov/2)×aspect00001tan⁡(fov/2)0000−far+nearfar−near−2×far×nearfar−near00−10]P_{persp} = \begin{bmatrix} \frac{1}{\tan(fov/2) \times aspect} & 0 & 0 & 0 \\ 0 & \frac{1}{\tan(fov/2)} & 0 & 0 \\ 0 & 0 & -\frac{far + near}{far - near} & -\frac{2 \times far \times near}{far - near} \\ 0 & 0 & -1 & 0 \\ \end{bmatrix}Ppersp= tan(fov/2)×aspect10000tan(fov/2)10000−far−nearfar+near−100−far−near2×far×near0

关键特性：
- x、y分量的变换：将视锥体横向、纵向范围映射到[-1,1]，aspect确保宽高比正确；
- z分量的变换：将[near, far]映射到NDC的[-1,1]（注意负号，因观察坐标z轴负方向为视线）；
- w分量：等于-z（观察坐标的z值），透视除法后，远处顶点的x、y会被缩小（实现近大远小）。

3. 正交投影矩阵（Orthographic Projection）：无透视效果

正交投影不会产生近大远小，物体大小与距离无关，适用于2D UI、工程图纸、CAD等场景。其裁剪体是一个"轴对齐的长方体"。

（1）正交投影的参数

构建正交投影矩阵需要六个参数（定义长方体的边界）：

left、right：x轴方向的左右边界；
bottom、top：y轴方向的上下边界；
near、far：z轴方向的近远边界。

（2）正交投影矩阵的公式

Portho=[2right−left00−right+leftright−left02top−bottom0−top+bottomtop−bottom00−2far−near−far+nearfar−near0001]P_{ortho} = \begin{bmatrix} \frac{2}{right - left} & 0 & 0 & -\frac{right + left}{right - left} \\ 0 & \frac{2}{top - bottom} & 0 & -\frac{top + bottom}{top - bottom} \\ 0 & 0 & -\frac{2}{far - near} & -\frac{far + near}{far - near} \\ 0 & 0 & 0 & 1 \\ \end{bmatrix}Portho= right−left20000top−bottom20000−far−near20−right−leftright+left−top−bottomtop+bottom−far−nearfar+near1

关键特性：
- x、y、z分量均为线性变换，直接将长方体范围映射到NDC的[-1,1]；
- w分量恒为1，透视除法后坐标不变，无透视效果。

4. 工程实践：构建投影矩阵的库函数

java 复制代码

// GLM库示例：构建透视投影矩阵
float fov = glm::radians(60.0f);    // 垂直视场角60°（转换为弧度）
float aspect = 16.0f / 9.0f;        // 16:9宽高比
float near = 0.1f;                  // 近裁剪面0.1
float far = 1000.0f;                // 远裁剪面1000
glm::mat4 projection = glm::perspective(fov, aspect, near, far);

// 构建正交投影矩阵（如2D UI，范围x:[-10,10], y:[-10,10], z:[-1,1]）
glm::mat4 orthoProjection = glm::ortho(-10.0f, 10.0f, -10.0f, 10.0f, -1.0f, 1.0f);

MVP矩阵的组合与渲染流水线中的应用

模型、视图、投影矩阵并非孤立存在，它们的组合（MVP矩阵）是3D渲染流水线的核心输入，决定了顶点从局部坐标到裁剪坐标的完整转换。

1. MVP矩阵的组合规则：P×V×M

由于矩阵乘法的"右结合性"，顶点的转换公式为：
裁剪坐标 = P × V × M × 局部坐标

计算顺序：局部坐标先乘M（到世界坐标），再乘V（到观察坐标），最后乘P（到裁剪坐标）；
矩阵组合顺序：MVP = P × V × M（先构建M，再V，最后P，按P×V×M顺序相乘）。

2. 在顶点着色器中的应用

在OpenGL/GLSL中，MVP矩阵通常作为uniform变量传入顶点着色器，直接用于转换顶点：

glsl 复制代码

// 顶点着色器（GLSL 300 es）
#version 300 es
uniform mat4 u_MVPMatrix;      // MVP矩阵（外部传入）
in vec4 a_Position;            // 局部坐标顶点（输入）

void main() {
    gl_Position = u_MVPMatrix * a_Position; // 计算裁剪坐标（内置输出）
}

gl_Position是顶点着色器的内置输出变量，存储裁剪坐标，后续会经透视除法转换为NDC。

3. MVP矩阵的工程意义

性能优化：CPU端预计算MVP矩阵，避免在顶点着色器中执行多次矩阵乘法（GPU更擅长并行处理顶点，而非复杂矩阵运算）；
渲染控制：通过修改MVP矩阵的组成，可实现丰富的视觉效果（如缩放场景、旋转相机、切换透视/正交模式）。

常见问题与避坑指南

1. 模型位置异常（偏移、缩放错误）

可能原因 ：
- 模型矩阵变换顺序错误（如先平移后旋转，导致模型绕世界原点旋转）；
- 缩放因子为0或负数（导致模型消失或镜像翻转）。
解决方案 ：严格遵循"缩放→旋转→平移"的顺序；确保缩放因子为正数且合理（如0.1~10）。

2. 相机视角异常（模型颠倒、视野过窄）

可能原因 ：
- 视图矩阵的up向量设置错误（如(0,-1,0)导致画面颠倒）；
- fov过大（如180°导致鱼眼效果）或过小（如10°导致视野过窄）。
解决方案 ：up向量通常设为(0,1,0)；fov建议在45°~60°（人眼舒适范围）。

3. 透视效果异常（模型拉伸、近大远小不明显）

可能原因 ：
- 透视投影的aspect与屏幕宽高比不匹配（如屏幕16:9，aspect设为4:3导致拉伸）；
- near与far差距过大（如near=0.1, far=10000导致远裁剪面附近精度不足，z-fighting）。
解决方案 ：aspect严格等于screenWidth/screenHeight；far不宜过大（根据场景需求设置，如室内场景设为100）。

4. 矩阵乘法顺序错误（最常见的坑）

错误示例 ：将MVP矩阵写为M×V×P，导致顶点先经投影变换，再视图变换，最后模型变换，完全违背坐标转换逻辑；
正确逻辑 ：MVP = P×V×M，顶点变换顺序为"局部→世界→观察→裁剪"。

总结

模型矩阵、视图矩阵、投影矩阵是3D渲染的"三大支柱"：

模型矩阵定义了模型在世界中的"姿态"（大小、朝向、位置），是场景构建的基础；
视图矩阵模拟了相机的"视角"，让3D世界有了"主观观察点"；
投影矩阵 决定了"可视范围"和"透视效果"，是连接3D空间与2D屏幕的最后一步。