分类与回归算法（三）- 逻辑回归

文章目录

一、逻辑回归相关理论
- [1. 为什么需要逻辑回归？](#1. 为什么需要逻辑回归？)
- - （1）输出值超出概率合理范围
  - （2）难以刻画分类边界的非线性特性
- [2. 逻辑回归的核心原理](#2. 逻辑回归的核心原理)
- - [2.1 Sigmoid 函数：从实数到概率的桥梁](#2.1 Sigmoid 函数：从实数到概率的桥梁)
  - [2.2 模型定义：从概率到分类](#2.2 模型定义：从概率到分类)
  - [2.3 损失函数](#2.3 损失函数)
二、逻辑回归的应用场景
- [1. 金融风控：风险预测的"守门人"](#1. 金融风控：风险预测的“守门人”)
- [2. 医疗诊断：辅助疾病筛查与预后](#2. 医疗诊断：辅助疾病筛查与预后)
- [3. 互联网运营：用户行为预测](#3. 互联网运营：用户行为预测)
- [4. 社会科学：基于数据的因果推断](#4. 社会科学：基于数据的因果推断)
三、逻辑回归实现步骤
- [1. 数据收集与加载](#1. 数据收集与加载)
- - [1.1 数据集介绍](#1.1 数据集介绍)
  - - [1.1.1 数据集基本信息](#1.1.1 数据集基本信息)
    - [1.1.2 数据集字段说明](#1.1.2 数据集字段说明)
  - [1.2 数据加载](#1.2 数据加载)
- [2. 数据探索与可视化（EDA）](#2. 数据探索与可视化（EDA）)
- - [2.1 数据基本信息](#2.1 数据基本信息)
  - - [2.1.1 查看数据前5行](#2.1.1 查看数据前5行)
    - [2.1.2 查看数据摘要信息](#2.1.2 查看数据摘要信息)
    - [2.1.3 描述性统计分析](#2.1.3 描述性统计分析)
    - [2.1.4 类别分布分析](#2.1.4 类别分布分析)
  - [2.2 单特征分布分析](#2.2 单特征分布分析)
  - [2.3 特征间关系分析](#2.3 特征间关系分析)
  - [2.4 特征相关性分析](#2.4 特征相关性分析)
- [3. 数据预处理](#3. 数据预处理)
- - [3.1 数据清洗](#3.1 数据清洗)
  - - [3.1.1 缺失值检测及处理](#3.1.1 缺失值检测及处理)
    - [3.1.2 异常值检测及处理](#3.1.2 异常值检测及处理)
  - [3.2 特征标准化](#3.2 特征标准化)
  - [3.3 数据集划分（训练集/测试集）](#3.3 数据集划分（训练集/测试集）)
- [4. 构建逻辑回归模型](#4. 构建逻辑回归模型)
- - [4.1 相关方法说明](#4.1 相关方法说明)
  - [4.2 构建逻辑回归模型](#4.2 构建逻辑回归模型)
- [5. 模型预测](#5. 模型预测)
- - [5.1 预测类别标签](#5.1 预测类别标签)
  - [5.2 预测类别概率](#5.2 预测类别概率)
- [6. 模型评估](#6. 模型评估)
- - [6.1 核心评估指标计算](#6.1 核心评估指标计算)
- [7. 结果可视化](#7. 结果可视化)
- - [7.1 混淆矩阵可视化](#7.1 混淆矩阵可视化)
  - [7.2 多分类ROC曲线与AUC](#7.2 多分类ROC曲线与AUC)
  - [7.3 特征权重可视化](#7.3 特征权重可视化)
- [8. 模型解释](#8. 模型解释)
- - [8.1 模型参数回顾](#8.1 模型参数回顾)
  - [8.2 特征权重的物理意义](#8.2 特征权重的物理意义)
  - [8.3 分类别解释模型决策逻辑](#8.3 分类别解释模型决策逻辑)
  - - [8.3.1 山鸢尾（setosa）](#8.3.1 山鸢尾（setosa）)
    - [8.3.2 变色鸢尾（versicolor）](#8.3.2 变色鸢尾（versicolor）)
    - [8.3.3 维吉尼亚鸢尾（virginica）](#8.3.3 维吉尼亚鸢尾（virginica）)
  - [8.4 核心结论](#8.4 核心结论)

一、逻辑回归相关理论

在机器学习领域，逻辑回归（Logistic Regression）虽名为"回归"，实则是一种结构简洁却功能强大的监督学习分类算法 ，尤其擅长处理二分类问题 ，例如：判断邮件是否为垃圾邮件、预测用户是否会点击广告、诊断患者是否患病等。尽管名称易引误解，它凭借模型可解释性强、训练效率高、预测结果稳定可靠等优势，广泛应用于金融风控、医疗诊断、用户流失预警等关键场景，成为数据科学家和工程师的首选工具之一。

1. 为什么需要逻辑回归？

理解逻辑回归，首先要明确它解决了什么问题。以一个典型场景为例：预测用户是否会点击某条广告（点击 = 1，不点击 = 0）。

若直接使用线性回归建模，会面临两个根本性问题：

（1）输出值超出概率合理范围

线性回归的输出是连续实数，例如：根据"用户年龄""浏览时长"等特征预测出"点击得分 = 1.2"或"-0.3"，但点击概率必须落在 [0, 1] 区间内。显然，线性回归无法满足这一基本要求。

（2）难以刻画分类边界的非线性特性

用户点击行为与特征之间的关系往往并非严格线性。例如，年轻用户点击率可能随浏览时长快速上升，而中年用户则增长缓慢。线性回归拟合的直线难以准确划分"点击"与"不点击"的决策边界。

为解决上述问题，逻辑回归应运而生------它在保留线性模型简洁性的同时，通过引入一个非线性映射函数 ，将线性输出转换为 [0,1] 区间内的概率值，从而完美适配分类任务。

2. 逻辑回归的核心原理

逻辑回归的本质是在线性模型基础上，通过非线性变换函数来实现二分类 。其核心围绕三个关键概念展开：Sigmoid 函数、线性组合、概率判定。

2.1 Sigmoid 函数：从实数到概率的桥梁

Sigmoid 函数（又称 Logistic 函数）是逻辑回归的"灵魂"。它将线性模型输出的任意实数 z ∈ ( − ∞ , + ∞ ) z \in (-\infty, +\infty) z∈(−∞,+∞)，压缩映射到 [0,1] 区间，赋予其概率解释。

其数学表达式为：
σ ( z ) = 1 1 + e − z \sigma(z) = \frac{1}{1 + e^{-z}} σ(z)=1+e−z1

其中 e ≈ 2.718 e \approx 2.718 e≈2.718 为自然常数， z z z 通常由线性组合给出：
z = w 1 x 1 + w 2 x 2 + ⋯ + w n x n + b = w ⊤ x + b z = w_1x_1 + w_2x_2 + \cdots + w_nx_n + b = \mathbf{w}^\top \mathbf{x} + b z=w1x1+w2x2+⋯+wnxn+b=w⊤x+b

这里：

x = [ x 1 , x 2 , ... , x n ] ⊤ \mathbf{x} = [x_1, x_2, \dots, x_n]^\top x=[x1,x2,...,xn]⊤ 是输入特征向量（如用户年龄、浏览时长等），
w = [ w 1 , w 2 , ... , w n ] ⊤ \mathbf{w} = [w_1, w_2, \dots, w_n]^\top w=[w1,w2,...,wn]⊤ 是对应特征的权重（反映特征对结果的影响程度），
b b b 是偏置项（截距），用于调整决策边界的位置。

Sigmoid 函数的特性：

Sigmoid函数的图像是一条平滑的"S型曲线"，有3个关键特性：

当 z → + ∞ z \to +\infty z→+∞ 时， σ ( z ) → 1 \sigma(z) \to 1 σ(z)→1：特征组合得分越高，属于正类的概率越接近 1；
当 z → − ∞ z \to -\infty z→−∞ 时， σ ( z ) → 0 \sigma(z) \to 0 σ(z)→0：得分越低，正类概率趋近于 0；
当 z = 0 z = 0 z=0 时， σ ( z ) = 0.5 \sigma(z) = 0.5 σ(z)=0.5：此时正负类概率相等。

例如：判断广告点击时，若Sigmoid输出=0.8，说明用户点击的概率是80%；若输出=0.2，则点击概率是20%。

2.2 模型定义：从概率到分类

结合 Sigmoid 函数，逻辑回归的完整概率模型如下：

正类（如"点击"）的概率： P ( y = 1 ∣ x ) = σ ( w T x + b ) = 1 1 + e − ( w T x + b ) P(y=1|x) = \sigma(w^Tx + b) = \frac{1}{1 + e^{-(w^Tx + b)}} P(y=1∣x)=σ(wTx+b)=1+e−(wTx+b)1
负类（如"不点击"）的概率： P ( y = 0 ∣ x ) = 1 − P ( y = 1 ∣ x ) P(y=0|x) = 1 - P(y=1|x) P(y=0∣x)=1−P(y=1∣x)

其中 w T x w^Tx wTx是特征与权重的内积（即 w T x = w 1 x 1 + w 2 x 2 + . . . + w n x n w^Tx=w_1x_1 + w_2x_2 + ... + w_nx_n wTx=w1x1+w2x2+...+wnxn）。

最终的分类规则： 设定一个阈值（默认0.5），若 P ( y = 1 ∣ x ) ≥ 阈值 P(y=1|x)≥阈值 P(y=1∣x)≥阈值，预测为正类；否则为负类。阈值可根据业务需求调整，比如在疾病诊断中，为避免漏诊（把患病判为健康），可将阈值调低（如0.3），让更多样本被判定为正类。

2.3 损失函数

和所有机器学习模型一样，逻辑回归需要通过最小化损失 来求解最优的权重 w w w 和截距 b b b 。损失是指模型预测概率与真实标签的差距。

（1）为什么不用均方误差（MSE）？

线性回归用MSE作为损失函数，但逻辑回归若用MSE，会导致损失函数变成非凸函数（图像有多个"小山峰"和"小山谷"），梯度下降容易陷入局部最小值，无法找到全局最优解。

（2）交叉熵损失

逻辑回归采用交叉熵损失（Cross-Entropy Loss） ，它是凸函数，能保证梯度下降找到全局最优解。其数学表达式为：
L o s s ( w , b ) = − 1 m ∑ i = 1 m [ y i log ⁡ ( P ( y i = 1 ∣ x i ) ) + ( 1 − y i ) log ⁡ ( 1 − P ( y i = 1 ∣ x i ) ) ] Loss(w,b) = -\frac{1}{m}\sum_{i=1}^m \left[ y_i\log(P(y_i=1|x_i)) + (1-y_i)\log(1-P(y_i=1|x_i)) \right] Loss(w,b)=−m1i=1∑m[yilog(P(yi=1∣xi))+(1−yi)log(1−P(yi=1∣xi))]其中 m m m是样本数， y i y_i yi是第 i i i个样本的真实标签（0或1）。

从直观上理解这个公式：

当 y i = 1 y_i=1 yi=1（真实是正类）：若模型预测 P = 1 P=1 P=1，则 log ⁡ ( P ) = 0 \log(P)=0 log(P)=0，损失为0；若 P → 0 P→0 P→0，则 log ⁡ ( P ) → − ∞ \log(P)→-∞ log(P)→−∞，损失急剧增大（惩罚错误预测）；
当 y i = 0 y_i=0 yi=0（真实是负类）：若模型预测 P = 0 P=0 P=0，则 log ⁡ ( 1 − P ) = 0 \log(1-P)=0 log(1−P)=0，损失为0；若 P → 1 P→1 P→1，则 log ⁡ ( 1 − P ) → − ∞ \log(1-P)→-∞ log(1−P)→−∞，损失急剧增大。

这种对错误预测严惩、对正确预测奖励的特性，正是逻辑回归能精准学习的关键。

"对错误预测严惩、对正确预测奖励" 通常出现在机器学习损失函数（Loss Function）设计 或模型优化目标 的语境中。它的核心思想是：通过设计合适的损失函数，引导模型更重视预测准确性，尤其在犯错时付出更大代价。

从损失函数的角度理解： 在监督学习中，模型通过最小化损失函数来学习参数。损失函数衡量的是预测值与真实值之间的差距。

"对错误预测严惩" ：当预测错误（比如分类错误、回归偏差大）时，损失函数值会显著增大，迫使模型在训练中"感受到痛"，从而调整参数避免再犯。
"对正确预测奖励" ：当预测准确（比如分类正确、回归误差小）时，损失函数值很小甚至为零，相当于模型"得到奖励"（即无需大幅调整参数）。

二、逻辑回归的应用场景

逻辑回归凭借可解释性强、训练高效、输出概率直观的特性，在工业界和学术界均有广泛应用。尤其在需要"明确决策依据"或"大规模数据快速部署"的场景中，它的优势远胜于黑盒模型（如深度学习）。以下是几个典型应用领域：

1. 金融风控：风险预测的"守门人"

金融领域对模型的可靠性和可解释性要求极高，逻辑回归是风控系统的核心工具：

信用评分：银行通过用户的收入、负债、征信记录等特征，用逻辑回归预测"用户违约概率"（1=违约，0=正常），据此决定是否放贷及贷款利率。例如：若模型输出违约概率=0.03（3%），则判定为低风险客户；若概率=0.7（70%），则拒绝放贷。
欺诈检测：信用卡公司实时分析交易金额、地点、时间等特征，用逻辑回归识别"欺诈交易概率"。当概率超过阈值（如0.8）时，立即冻结卡片并提醒用户，有效降低盗刷损失。

逻辑回归的参数（权重）可直接解释风险因素：例如"近期异地大额交易"的权重为正且绝对值大，说明该特征会显著提高欺诈概率，为风控规则制定提供明确依据。

2. 医疗诊断：辅助疾病筛查与预后

在医疗场景中，逻辑回归帮助医生将"症状数据"转化为"患病概率"，辅助决策：

疾病筛查：通过患者的年龄、血压、血糖、家族病史等特征，预测"患糖尿病/心脏病的概率"。例如：模型输出某患者患病概率=0.65，结合临床经验，医生可建议进一步检查。
预后分析：对癌症患者，根据肿瘤大小、分期、治疗方案等特征，预测"术后复发概率"，为后续治疗方案调整提供参考（如复发概率高则需加强随访）。

医疗场景对"错误预测的代价"敏感（如漏诊比误诊更危险），逻辑回归可灵活调整分类阈值（如将默认0.5调低至0.3），优先保证"真实患者被检出"（高召回率）。

3. 互联网运营：用户行为预测

互联网公司依赖用户行为数据优化产品策略，逻辑回归是用户分析的"利器"：

用户增长：预测"新用户7天内留存概率"（1=留存，0=流失），结合"注册渠道""首屏停留时间"等特征，识别高留存潜力用户，针对性推送福利。
精准营销：在电商平台中，根据用户的浏览记录、加购行为、历史购买金额等，预测"对某商品的点击/购买概率"，实现广告或优惠券的精准投放（如向购买概率＞0.4的用户推送折扣）。

逻辑回归训练速度快（毫秒级），可实时处理亿级用户数据，满足互联网场景的高并发需求。

4. 社会科学：基于数据的因果推断

在社会学、经济学等领域，逻辑回归常用于分析"影响因素与结果的关系"：

教育领域：研究"家庭收入、父母学历"等特征对"学生考上大学的概率"的影响，权重为正的特征（如父母学历高）说明其对结果有促进作用。
公共政策：分析"就业政策、地区经济水平"等因素与"居民脱贫概率"的关联，为政策调整提供数据支持（如某政策的权重显著为正，说明其有效提升脱贫概率）。

逻辑回归的参数可量化特征的影响程度（如"每增加1万元家庭收入，考上大学的概率提升2%"），这是黑盒模型难以替代的优势。

三、逻辑回归实现步骤

1. 数据收集与加载

1.1 数据集介绍

1.1.1 数据集基本信息

本示例使用的鸢尾花数据集（Iris Dataset） 是机器学习领域最经典的数据集之一，由英国统计学家和生物学家罗纳德·费希尔（Ronald Fisher）于1936年提出。该数据集包含3种鸢尾花亚种的特征数据，适合用于多分类任务的逻辑回归模型演示，具体信息如下：

样本数量：共150个样本，3个类别（每种鸢尾花各50个样本）。
类别标签 ：
- 0：山鸢尾（setosa）
- 1：变色鸢尾（versicolor）
- 2：维吉尼亚鸢尾（virginica）
特征变量 ：4个数值型特征（单位：厘米），均为鸢尾花的形态学测量数据：
- 花萼长度（sepal length）
- 花萼宽度（sepal width）
- 花瓣长度（petal length）
- 花瓣宽度（petal width）
数据特点 ：特征均为连续数值型，无缺失值，噪声小，类别间区分度较高（尤其 setosa 与其他两类线性可分）

注：虽然逻辑回归原生适用于二分类，但通过 One-vs-Rest（OvR） 策略可自然扩展至多分类，Scikit-learn 中的 LogisticRegression 默认支持多分类。

1.1.2 数据集字段说明

字段名称（英文）	中文含义	数据类型	单位	说明
`sepal length (cm)`	花萼长度	浮点数	厘米	花朵最外层保护结构的长度
`sepal width (cm)`	花萼宽度	浮点数	厘米	花萼的横向宽度
`petal length (cm)`	花瓣长度	浮点数	厘米	花朵内层显眼部分的长度
`petal width (cm)`	花瓣宽度	浮点数	厘米	花瓣的横向宽度
`species`	类别标签	对象	---	0 = setosa, 1 = versicolor, 2 = virginica

所有特征均为形态学测量值，具有明确的生物学意义，且数值范围相近，适合直接用于建模（必要时可标准化）。

1.2 数据加载

在 Python 中，可通过 scikit-learn 库直接加载鸢尾花数据集，无需手动下载或解析文件：

python 复制代码

import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from sklearn.datasets import load_iris

# 设置matplotlib的中文字体为SimHei（黑体），以确保中文标签可以正常显示。
plt.rcParams['font.sans-serif'] = ['SimHei']
# 解决负号'-'显示为方块的问题，通过设置'axes.unicode_minus'为False来实现。
plt.rcParams['axes.unicode_minus'] = False

# 设置全局选项
pd.set_option('display.max_columns', None)  # 显示所有列
pd.set_option('display.width', None)  # 自动检测宽度
pd.set_option('display.max_colwidth', 50)  # 列内容最多显示50字符
pd.set_option('display.expand_frame_repr', False)  # 禁用多行表示（可选）

# 加载数据集
iris = load_iris()
# 特征矩阵 X：150 行 × 4 列
X = iris.data  
# 目标标签 y：150 个整数（0, 1, 2）
y = iris.target  
# 特征名称和类别名称（用于后续分析）
feature_names = iris.feature_names
target_names = iris.target_names

2. 数据探索与可视化（EDA）

数据探索与可视化（Exploratory Data Analysis, EDA）是建模前的关键步骤，通过分析数据分布、特征关系和类别差异，可帮助理解数据规律，为后续模型优化提供依据。

2.1 数据基本信息

数据基本信息分析旨在快速了解数据集的结构、特征类型、统计分布及类别平衡情况，为后续处理奠定基础。

2.1.1 查看数据前5行

通过查看数据集前几行，可直观了解特征的数值范围、数据格式及样本结构。代码如下：

python 复制代码

import pandas as pd

# 将特征、标签转换为DataFrame（结合特征名称和类别名称）
iris_df = pd.DataFrame(
    data=X,  # 特征数据（花萼长度、宽度等）
    columns=feature_names  # 特征名称列表
)
iris_df['species'] = [target_names[i] for i in y]  # 添加类别名称列

# 查看前5行数据
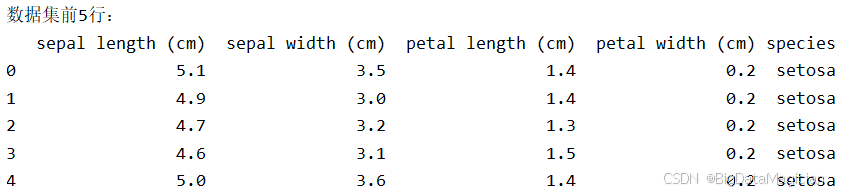
print("数据集前5行：")
print(iris_df.head())

输入结果如下图所示，数据集中每个样本包含4个数值型特征（单位为厘米）和1个类别标签（物种名称）。前5行样本均为setosa（山鸢尾），特征值在较小范围内波动（如花瓣长度集中在1.3-1.5cm）。

2.1.2 查看数据摘要信息

通过info()方法可获取数据集的基本结构信息，包括样本数量、特征类型、是否存在缺失值等。代码如下：

python 复制代码

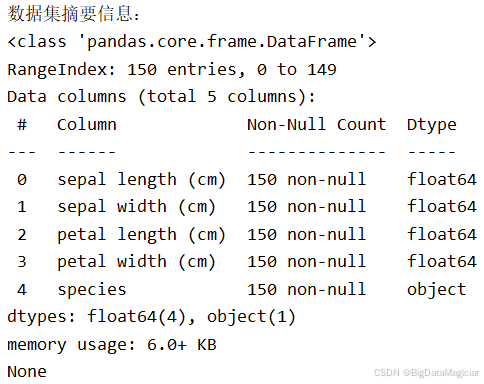
print("\n数据集摘要信息：")
print(iris_df.info())

输入结果如下图所示，数据集共150个样本，5列数据（4个特征+1个类别）。所有特征均为float64类型（数值型），类别列species为object类型（字符串）。无缺失值（Non-Null Count均为150），无需进行缺失值处理。

2.1.3 描述性统计分析

通过describe()方法可计算数值型特征的统计量（如均值、标准差、分位数等），反映特征的分布特征。代码如下：

python 复制代码

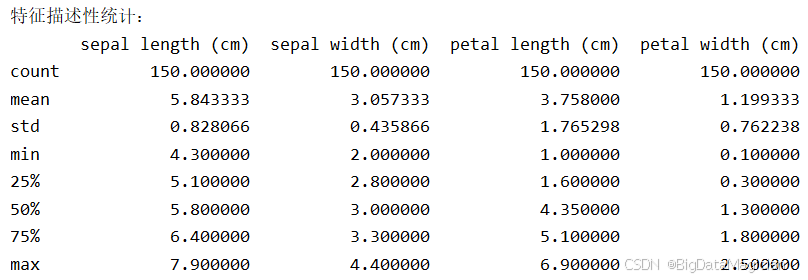
print("\n特征描述性统计：")
print(iris_df.describe())

输入结果如下图所示，每个特征均包含150个样本，其中花萼长度平均值为5.84 cm，标准差0.83 cm，范围4.3 cm--7.9 cm；花萼宽度平均值为3.06 cm，标准差0.44 cm，范围2.0--4.4 cm；花瓣长度平均值为3.75 cm，标准差1.77 cm，范围1.0--6.9 cm；花瓣宽度平均值为1.19 cm，标准差0.76 cm，范围0.1--2.5 cm。中位数（50%分位数）与均值接近，说明特征分布较对称，无严重偏态。从标准差来看，花瓣长度相对其他特征较大，说明其数值变化更大。从四分位数来看，各特征分布较为集中，无明显异常值，且花瓣长度变异程度相对较大，表明其在不同类别间可能具有更强的区分能力，适合用于分类建模。

小知识：

均值（Mean）和中位数（Median）的定义

均值：所有数据的算术平均值，对极端值（异常值）敏感。

中位数 ：将数据从小到大排序后，处于中间位置的值，对极端值不敏感，只反映"位置中心"。

对称分布 vs 偏态分布
对称分布（如正态分布）: 数据在中心两侧均匀分布，均值 = 中位数 = 众数 。例如：[1, 2, 3, 4, 5] → 均值 = 3，中位数 = 3。
右偏（正偏态）分布： 尾部向右拉长（存在较大的极端值），均值 > 中位数 （因为大值把均值"拉高"了）。例如：[1, 2, 3, 4, 20] → 均值 = 6，中位数 = 3。
左偏（负偏态）分布： 尾部向左拉长（存在较小的极端值），均值 < 中位数。例如：[-10, 1, 2, 3, 4] → 均值 = 0，中位数 = 2。

2.1.4 类别分布分析

分析类别分布可判断数据集是否均衡（类别样本数量差异过大可能影响模型性能）。代码如下：

python 复制代码

print("\n类别分布：")
print(iris_df['species'].value_counts())

plt.figure(figsize=(6, 4))
# 使用 seaborn 绘制类别计数柱状图，展示鸢尾花三个物种的样本数量分布
sns.countplot(x='species', data=iris_df, palette='Set3')
plt.title('Distribution of Iris Species')
plt.xlabel('Species')
plt.ylabel('Count')
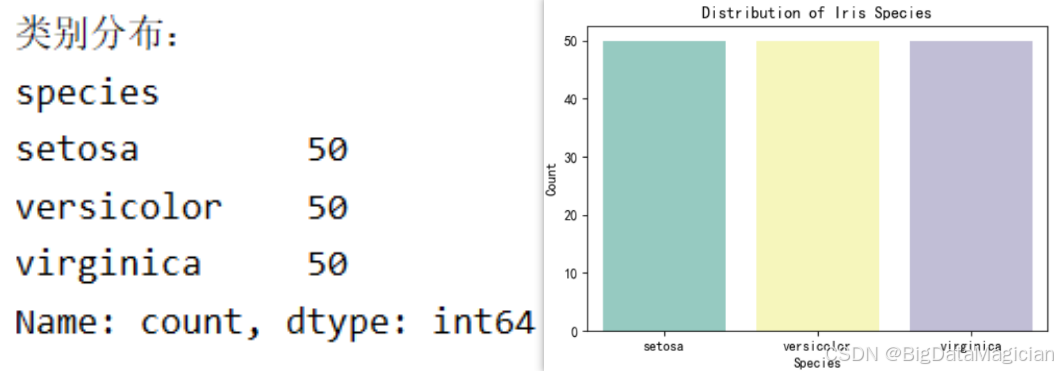
plt.show()

输入结果如下图所示，鸢尾花数据集包含3个类别，每个类别均有50个样本，属于完全均衡的数据集，无需进行类别平衡处理（如过采样、欠采样）。均衡的类别分布可保证模型训练时不会因某类样本过多而偏向该类，有利于提高模型的泛化能力。

2.2 单特征分布分析

使用 Seaborn 的 kdeplot 函数绘制鸢尾花数据集中四个特征（花萼长度、花萼宽度、花瓣长度、花瓣宽度）的核密度估计图（KDE），并按物种（species）进行分组着色。通过设置 hue='species'、fill=True 和 alpha=0.5，每类物种的密度曲线以半透明填充形式叠加显示；common_norm=False 确保每个物种的密度曲线独立归一化（即每条曲线下的面积均为1），从而公平比较各类别内部的分布形态而非受样本量影响。四个子图以 2×2 网格布局呈现，最终图像保存为 iris_kde_distribution.png，便于后续分析各特征在不同类别间的分布差异。

python 复制代码

# 绘制核密度图，KDE：核密度估计
plt.figure(figsize=(15, 10))
feature = iris_df.columns[:-1]
for i in range(len(feature)):
    plt.subplot(2, 2, i + 1)
    sns.kdeplot(
        data=iris_df,
        x=feature[i],
        hue='species',
        fill=True,
        common_norm=False,  # 每个类别单独归一化
        alpha=0.5
    )
    plt.title(f'KDE Distribution of {feature[i]} by Species')
    plt.xlabel(feature[i])
# plt.show()
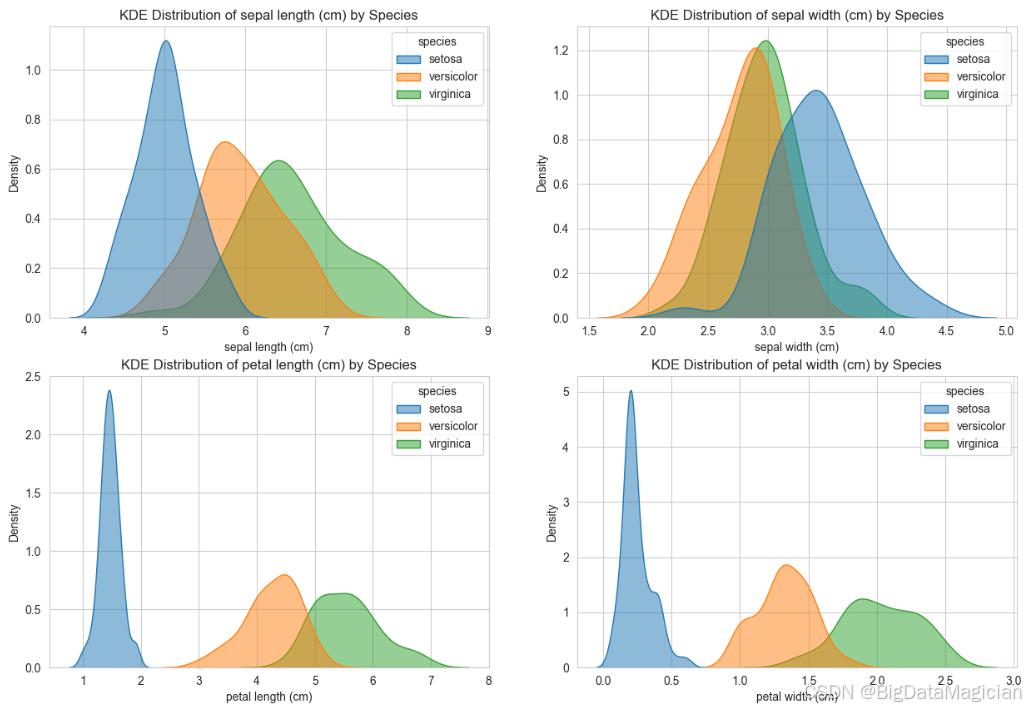
plt.savefig('iris_kde_distribution.png')

运行结果如下图所示，从图中可以得出：

花瓣长度（Petal Length） 特征展现出极强的类别区分能力。Setosa 物种的分布高度集中于 1.0--2.0 cm 区间，形成一个尖锐且孤立的峰值；Versicolor 主要分布在 3.5--5.0 cm，而 Virginica 则集中在 4.7--6.2 cm。三者之间重叠较少，尤其是 Setosa 与其他两类完全分离，表明花瓣长度是识别鸢尾花种类的强有力指标。

花瓣宽度（Petal Width） 同样具有优异的判别性能。Setosa 的分布集中在 0.1--0.5 cm，明显区别于其他两类；Versicolor 位于 1.0--1.6 cm，Virginica 则在 1.5--2.5 cm。尽管 Versicolor 与 Virginica 在 1.5--1.8 cm 区间存在轻微重叠，但整体分布仍清晰可辨，适合用于分类建模。

花萼长度（Sepal Length） 三类物种的分布存在显著重叠。Setosa 峰值在 4.8--5.2 cm，Versicolor 在 5.5--6.5 cm，Virginica 在 6.0--7.0 cm。后两者在 6.0--6.5 cm 区间高度交叉，导致仅凭花萼长度难以准确区分 Versicolor 与 Virginica，其分类价值相对有限。

花萼宽度（Sepal Width） 该特征的区分能力最弱。Setosa 分布于 3.0--3.8 cm，Versicolor 在 2.3--3.2 cm，Virginica 覆盖 2.5--3.4 cm，三者在 3.0--3.5 cm 区域严重重叠。密度曲线形状相近且峰值接近，表明花萼宽度单独使用时难以有效分离不同物种，需结合其他特征提升判别效果。

2.3 特征间关系分析

使用 Seaborn 的 pairplot 函数绘制鸢尾花数据集的散点图矩阵 ，用于全面分析四个数值特征之间的两两关系及其与物种分类的关联。通过设置 hue='species'，将不同物种以不同颜色标记（setosa: 蓝色，versicolor: 橙色，virginica: 绿色），直观展示类别在多维空间中的分布模式；corner=True 避免对称重复，仅显示下三角区域的散点图，提升可读性；diag_kind='kde' 在对角线位置用核密度估计图（KDE）展示各特征的单变量分布，增强整体信息密度。最终生成的图表综合呈现了特征间的相关性、聚类趋势和分类边界，是探索性数据分析（EDA）中高效的可视化工具。

python 复制代码

# 绘制所有特征的散点图矩阵（快速查看多特征关系）
sns.pairplot(
    iris_df,
    hue='species',
    corner=True,  # 只显示下三角，避免重复
    diag_kind='kde'  # 对角线用核密度图
)
plt.suptitle('Pairwise Relationships Between Features', y=1.02)
plt.savefig('iris_pairplot.png')

运行结果如下图所示，从图中可以得出：

花瓣长度与花瓣宽度 两个特征高度正相关，且三类物种形成明显分离的簇。Setosa 集中在左下角（花瓣短小），与其他两类无重叠；Versicolor 分布在中间区域；Virginica ：位于右上角（花瓣长宽均较大）。这表明花瓣长度与宽度组合能极好地区分所有物种，是构建分类模型的关键特征对。

花萼长度与花瓣长度： Setosa 在花瓣长度较小（<2 cm）时，花萼长度集中在 4.5--6 cm；Versicolor 和 Virginica 的花瓣长度显著更大，且随花瓣长度增加，花萼长度也呈上升趋势；但 Versicolor 与 Virginica 在花萼长度上仍有部分重叠，说明仅凭此组合无法完全区分两者。

花萼长度与花萼宽度： 三类物种在此平面上分布较密集，尤其 Versicolor 与 Virginica 存在明显重叠；Setosa 倾向于较小的花萼宽度（约 3.0--3.5 cm），而 Virginica 的花萼宽度更宽；整体来看，该特征组合的分类能力较弱，难以实现清晰划分。

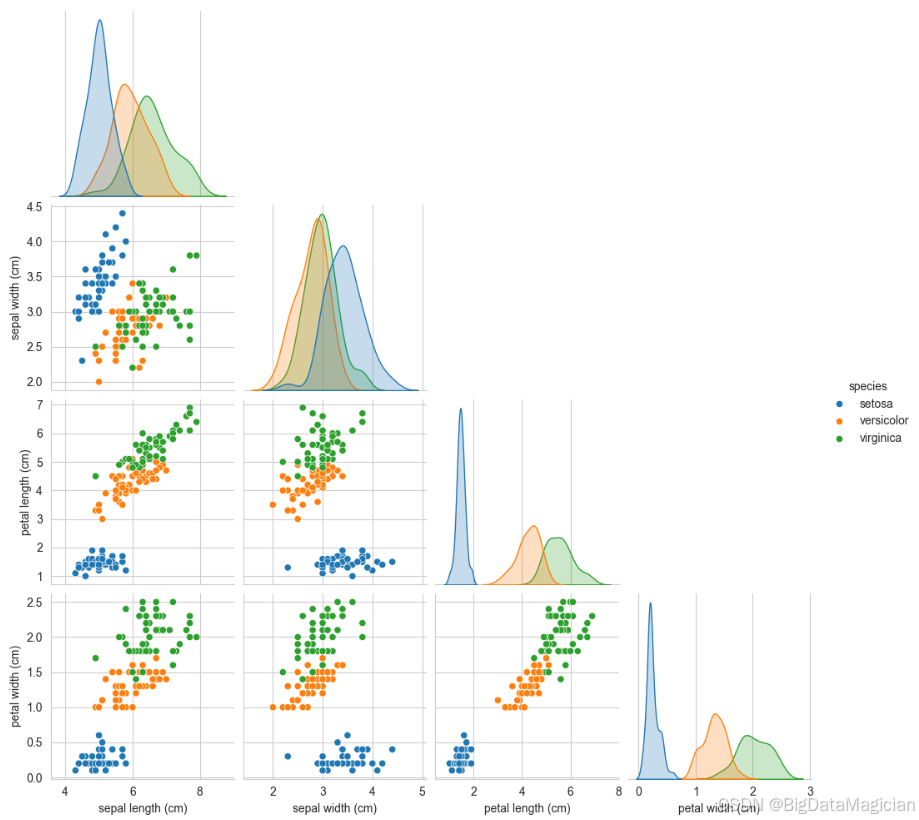
从图中可以得出花瓣长度与花瓣宽度呈强正相关，且两类特征结合可清晰区分山鸢尾与其他两类；变色鸢尾和维吉尼亚鸢尾在花瓣特征上有少量重叠，是模型可能出错的主要区域。花萼特征（长度、宽度）的区分能力较弱，但花萼宽度在山鸢尾中普遍更大（可作为辅助区分特征）。

2.4 特征相关性分析

该代码用于计算鸢尾花数据集中四个数值特征之间的皮尔逊相关系数矩阵 ，并使用热力图进行可视化。通过 iris_df.iloc[:, :-1] 提取除类别列外的所有特征，调用 .corr() 方法计算两两特征间的线性相关性；随后利用 sns.heatmap() 绘制热力图，其中 annot=True 显示具体数值，cmap='coolwarm' 以红蓝渐变表示正负相关，vmin=-1, vmax=1 确保颜色范围完整覆盖相关系数区间，square=True 使每个单元格为正方形，提升可读性。最终生成的热力图直观展示了各特征之间的线性关联强度，有助于识别冗余特征和构建更高效的模型。

python 复制代码

# 计算特征间的相关系数（皮尔逊系数）
corr_matrix = iris_df.iloc[:, :-1].corr()  # 排除类别列

# 绘制热力图
plt.figure(figsize=(8, 6))
sns.heatmap(
    corr_matrix,
    annot=True,  # 显示相关系数值
    cmap='coolwarm',
    vmin=-1, vmax=1,  # 颜色范围
    square=True
)
plt.title('Correlation Matrix of Features')
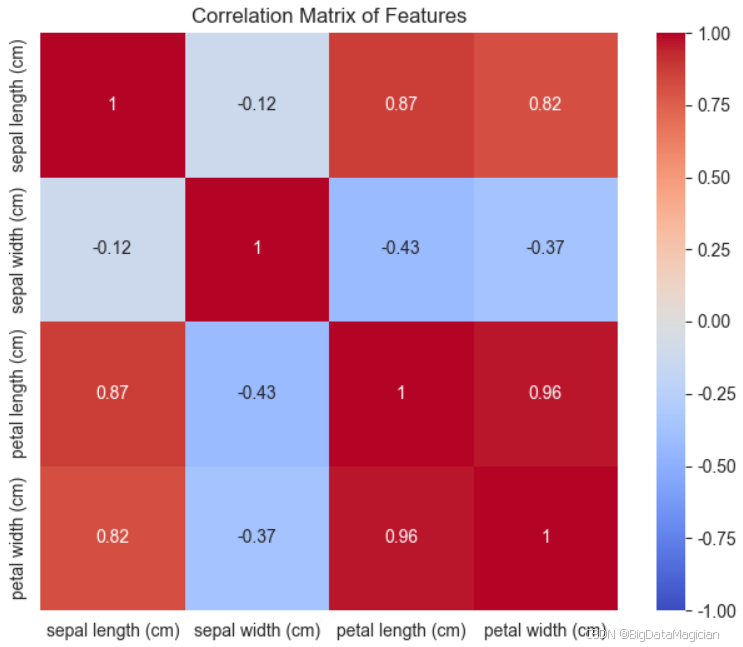
plt.savefig('iris_correlation_matrix.png')

运行结果如下图所示，从图中可以得出：

花瓣长度与花瓣宽度高度正相关（0.96）

两者之间存在极强的正线性关系，表明花瓣的长度和宽度通常同步变化；
这说明这两个特征携带的信息高度重叠，在建模时若同时使用可能导致多重共线性问题；
可考虑仅保留其中一个作为代表特征，或通过主成分分析（PCA）降维处理；
但因特征维度低，对逻辑回归模型影响较小（逻辑回归对轻度共线性不敏感）。

花瓣长度与花萼长度正相关（0.87）

花瓣长度越大，花萼长度也趋于增加，但相关性略低于花瓣自身组合；
表明植物整体尺寸存在一致性趋势，但仍有一定独立性；
二者可共同用于分类，但需注意其协同效应可能影响模型解释性。

花瓣宽度与花萼长度正相关（0.82）

同样呈现较强的正相关，进一步验证了"大花"整体结构的一致性；
说明花萼长度虽非主导特征，但在一定程度上反映了花朵大小信息。

花萼长度与花萼宽度弱相关（-0.12）

两者几乎不相关，甚至轻微负相关，说明花萼的长短与宽窄无明显线性依赖；
表明这两个特征提供了相对独立的信息，可以同时保留用于建模。

花瓣长度与花萼宽度弱负相关（-0.43）

存在中等程度的负相关，即花瓣越长，花萼宽度可能越小；
反映出某些物种（如 setosa）具有短花瓣、宽花萼的特点，而其他物种则相反；
虽非强相关，但仍提示存在一定的生物形态规律。

花瓣宽度与花萼宽度弱负相关（-0.37）

类似地，花瓣宽度越大，花萼宽度越小，但相关性较弱；
进一步支持不同物种在形态上的差异性分布。

3. 数据预处理

数据预处理是建模的核心步骤之一，目的是将原始数据转换为适合模型训练的格式，减少噪声、消除冗余，提升模型的训练效率和预测精度。

3.1 数据清洗

在机器学习与数据分析流程中，数据清洗是确保模型性能和结果可靠性的关键前置步骤。原始数据往往存在缺失值、异常值、重复记录或格式不一致等问题，若未加以处理，将直接影响后续特征工程、建模及预测的准确性。因此，在开展任何分析之前，必须对数据进行全面的清洗与预处理。

3.1.1 缺失值检测及处理

缺失值是指数据集中某些变量在特定样本上缺少观测值的情况。其存在可能导致统计偏差、降低模型泛化能力，甚至引发算法报错（如某些模型无法处理空值）。为保障数据完整性，首先进行系统性缺失值检测。此处采用 Python 中的 pandas 库对鸢尾花数据集（Iris Dataset）执行缺失值检查。实现代码如下：

python 复制代码

# 1. 缺失值检查（再次确认，避免遗漏）
print("缺失值统计：")
print(iris_df.isnull().sum())

运行结果如下图所示，所有特征列（包括花萼长度、花萼宽度、花瓣长度、花瓣宽度）以及目标变量（species）的缺失值均为 0，表明该数据集无任何缺失值，数据完整且结构良好，无需进行缺失值填充或删除等处理。

3.1.2 异常值检测及处理

在数据清洗过程中，异常值（Outliers）是指与大多数观测值显著偏离的数据点。它们可能是由测量误差、录入错误或真实但极端的自然变异引起的。异常值若未被合理处理，可能对模型训练造成干扰，导致模型过拟合或预测偏差。因此，在建模前进行系统性的异常值检测与处理至关重要。

本研究采用箱线图（Boxplot）对鸢尾花数据集中的四个数值特征进行可视化分析，以识别潜在的异常值。箱线图基于五数概括法（最小值、第一四分位数 Q1、中位数 Q2、第三四分位数 Q3、最大值），并通过"四分位距"（IQR = Q3 - Q1）定义异常值边界。实现代码如下所示，使用 Seaborn 的 boxplot 函数生成所有特征的箱线图。

python 复制代码

plt.figure(figsize=(10, 6))
sns.boxplot(data=iris_df.iloc[:, :-1])  # 排除类别列，展示所有特征的箱线图
plt.title('Boxplot of Iris Features (Outlier Detection)')
plt.xticks(rotation=45)
plt.tight_layout()
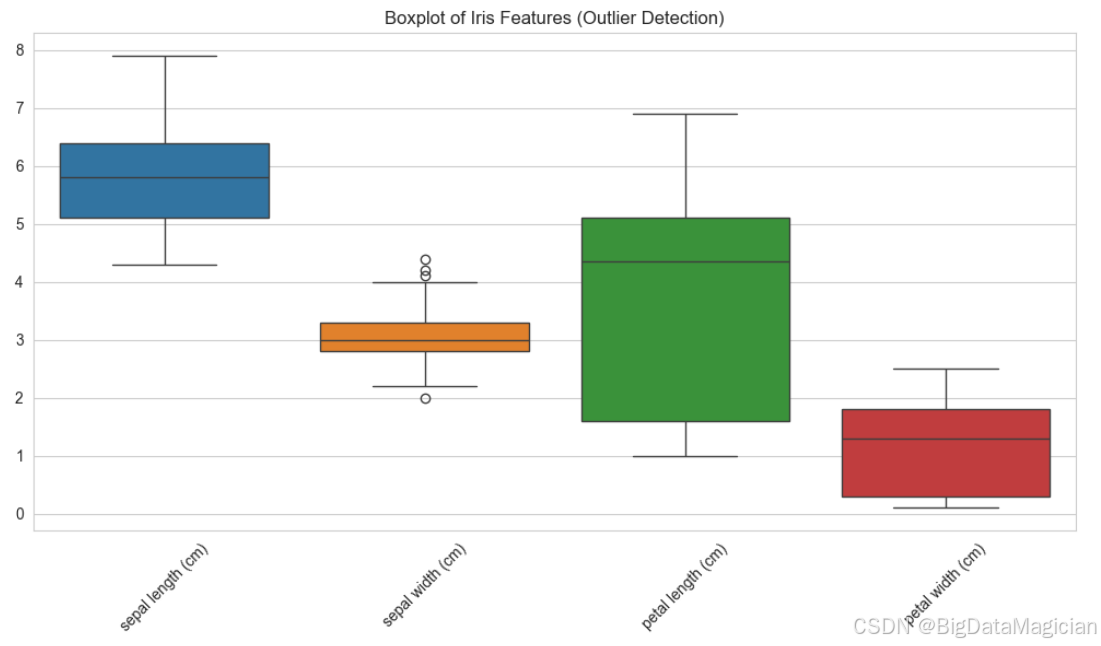
plt.savefig('iris_boxplot.png')

运行结果如下图所示，每个箱体表示中间 50% 的数据分布，中位数以横线显示，"须"延伸至非异常值的最大/最小值，圆圈标记为超出上下界的异常点；从图中可看出花萼宽度中发现少量疑似异常点，但从生物学角度判断，这些值仍在合理范围内，应视为有效数据，不应剔除。整体来看，鸢尾花数据集无严重异常值，数据质量较高。

3.2 特征标准化

在机器学习中，逻辑回归等基于梯度下降优化的模型对特征的数值尺度高度敏感。若不同特征的取值范围差异较大（如花萼长度在4--8之间，而花瓣宽度仅0.1--2.5），会导致损失函数等高线呈狭长形状，使梯度下降收敛缓慢，甚至造成模型系数权重失衡。为解决此问题，采用Z-score标准化将每个特征转换为均值为0、标准差为1的分布，从而消除量纲影响，提升模型训练效率与稳定性。

实现代码如下图所示，代码首先导入并初始化StandardScaler标准化器，随后对鸢尾花数据集中除类别标签外的四个数值特征执行fit_transform()操作，计算各特征的均值和标准差，再据此进行标准化变换；接着将结果转换为DataFrame以便保留列名，并输出标准化后的前五行数据及整体统计量，用于验证处理效果。

python 复制代码

# 初始化标准化器
scaler = StandardScaler()
# 训练集特征标准化：拟合+转换
X_scaled = scaler.fit_transform(iris_df.iloc[:, :-1])
# 转换为DataFrame便于查看
X_scaled_df = pd.DataFrame(X_scaled, columns=iris_df.columns[:-1])
# 查看标准化后的训练集特征统计量
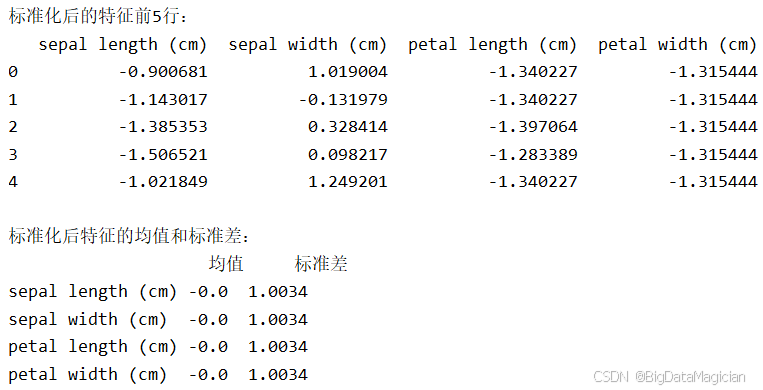
print("\n标准化后的特征前5行：")
print(X_scaled_df.head())
print("\n标准化后特征的均值和标准差：")
print(pd.DataFrame({
    "均值": X_scaled_df.mean().round(4),
    "标准差": X_scaled_df.std().round(4)
}))

运行结果如下图所示，输出结果显示，标准化后所有特征的均值接近0、标准差接近1，符合预期。例如，原始花瓣长度（均值约3.76）被转换为以0为中心的数值，其极端值也缩放到合理区间。这表明标准化成功消除了原始特征间的量级差异，为后续逻辑回归等模型提供了统一且稳定的输入空间，有助于提升模型性能与泛化能力。

3.3 数据集划分（训练集/测试集）

在机器学习流程中，将原始数据划分为训练集和测试集是评估模型泛化能力的关键步骤。训练集用于拟合模型参数，测试集则用于独立评估模型性能，避免过拟合带来的乐观估计。为确保评估结果的客观性和代表性，需保证训练集与测试集中各类别的比例与原始数据一致，尤其是在类别不平衡场景下。为此，采用分层抽样（stratified sampling）策略，使每类样本在训练集和测试集中按原分布比例分配，从而提升模型评估的可靠性。

实现代码如下图所示，该代码使用 train_test_split 函数将已标准化的特征矩阵 X_scaled 与标签向量 y 按照 7:3 的比例划分为训练集和测试集。其中，test_size=0.3 设置测试集占比，random_state=42 固定随机种子以保证实验可复现；关键参数 stratify=y 实现分层抽样，确保每个类别在训练集和测试集中的分布与原始数据保持一致。最后输出各子集的形状信息，便于验证划分是否正确。

python 复制代码

# 划分比例：训练集70%，测试集30%，设置随机种子保证结果可复现
X_train, X_test, y_train, y_test = train_test_split(
    X_scaled, y,
    test_size=0.3,
    random_state=42,
    stratify=y  # 按类别分层抽样，保持类别分布均衡
)

# 打印划分后的数据规模
print(f"\n训练集特征形状：{X_train.shape}，测试集特征形状：{X_test.shape}")
print(f"训练集标签形状：{y_train.shape}，测试集标签形状：{y_test.shape}")

划分结果如下图所示，训练集包含 105 个样本（特征维度为 4），测试集包含 45 个样本，符合 7:3 的比例要求。标签形状分别为 (105,) 和 (45,)，表明样本数量匹配。由于使用了 stratify=y，三类鸢尾花（setosa、versicolor、virginica）在训练集和测试集中均保持约 1:1:1 的均衡分布，有效避免了因随机划分导致的类别偏差，为后续模型评估提供了稳定且可信的基础。

4. 构建逻辑回归模型

4.1 相关方法说明

4.2 构建逻辑回归模型

逻辑回归是一种广泛应用于分类任务的线性模型，其核心是通过Sigmoid函数将线性组合的输出映射为概率值。在多分类问题中，如鸢尾花数据集包含三个类别（setosa、versicolor、virginica），需采用多项式逻辑回归（multinomial logistic regression）策略，直接建模每个类别的概率分布。本研究使用 sklearn.linear_model.LogisticRegression 构建模型，设置 multi_class='multinomial' 启用多项式逻辑回归，并选择 solver='lbfgs' 优化器以适应多分类场景；同时增加 max_iter=200 避免收敛不足，设定 random_state=42 确保实验可复现，正则化参数 C=1.0 控制模型复杂度，防止过拟合。

实现代码如下图所示，首先初始化逻辑回归模型并配置关键参数，随后调用 fit(X_train, y_train) 方法在标准化后的训练集上进行训练，学习各特征对不同类别的影响权重。训练完成后，提取模型的截距（intercept_）和系数矩阵（coef_），其中截距对应每个类别的偏置项，系数表示每个特征在该类别预测中的重要性。接着将这些参数整理为DataFrame，按类别命名行索引，便于后续分析与解释，最终输出结构化的模型参数表。

python 复制代码

# 初始化逻辑回归模型（多分类配置）
model = LogisticRegression(
    multi_class='multinomial',  # 多项式逻辑回归（直接建模多分类概率）
    solver='lbfgs',  # 适合多分类的优化求解器
    max_iter=200,  # 迭代次数（默认100可能不收敛，适当增加）
    random_state=42,  # 随机种子，保证结果可复现
    C=1.0  # 正则化强度（C越小正则化越强，默认1.0）
)

# 训练模型（输入标准化后的训练集）
model.fit(X_train, y_train)

# 查看模型核心参数
print("\n模型截距（每个类别对应一个截距）：")
print(model.intercept_)
print("\n模型系数（每个类别对应4个特征的权重）：")
for i, class_name in enumerate(target_names):
    print(f"{class_name}：{model.coef_[i]}")

# 提取模型参数
intercepts = model.intercept_  # 每个类别的截距
coef = model.coef_     # 每个类别对应的特征系数（形状：[3,4]，3个类别×4个特征）
print(intercepts)
# 构建DataFrame：行索引为类别名称，列包含"截距"和4个特征
param_df = pd.DataFrame(
    data=coef,
    index=target_names,
    columns=feature_names
)
param_df.insert(loc=0, column='截距', value=intercepts)  # 在第1列插入截距

# 打印结果
print("每个类别对应的截距及特征权重：")
print(param_df.round(4))  # 保留4位小数，便于阅读

运行结果如下图所示，从输出的参数表可见，每个类别均有一个独立的截距和四个特征权重。例如，setosa 类别的截距为 -0.2471，花瓣长度和宽度的系数分别为 -1.6738 和 -1.5893，表明这两个特征在区分 setosa 时具有显著负向作用（即值越小越可能属于 setosa）。而 virginica 的花瓣长度和宽度系数分别为 1.7962 和 2.3884，呈强正相关，说明大花瓣更倾向于该类别。整体来看，花瓣相关特征在各类别中权重绝对值较大，体现了其在分类决策中的主导地位，而花萼特征影响较弱，验证了前期探索性分析的结论。

5. 模型预测

5.1 预测类别标签

在模型训练完成后，使用测试集进行预测是评估其分类能力的关键步骤。通过调用 model.predict() 方法，直接输出每个测试样本的预测类别（即鸢尾花的种类），并将结果转换为人类可读的字符串形式，便于后续分析和验证。由于原始标签为数值编码（0、1、2 分别对应 'setosa'、'versicolor' 和 'virginica'），因此需要将其映射回对应的物种名称，以增强结果的可解释性。

python 复制代码

# 对测试集进行类别预测
y_pred = model.predict(X_test)

# 将真实标签和预测标签转换为类别名称（字符串）
y_test_names = [target_names[i] for i in y_test]
y_pred_names = [target_names[i] for i in y_pred]

# 构建 DataFrame
comparison_df = pd.DataFrame({
    '真实物种': y_test_names,
    '预测物种': y_pred_names
})

# 保存为 CSV 文件
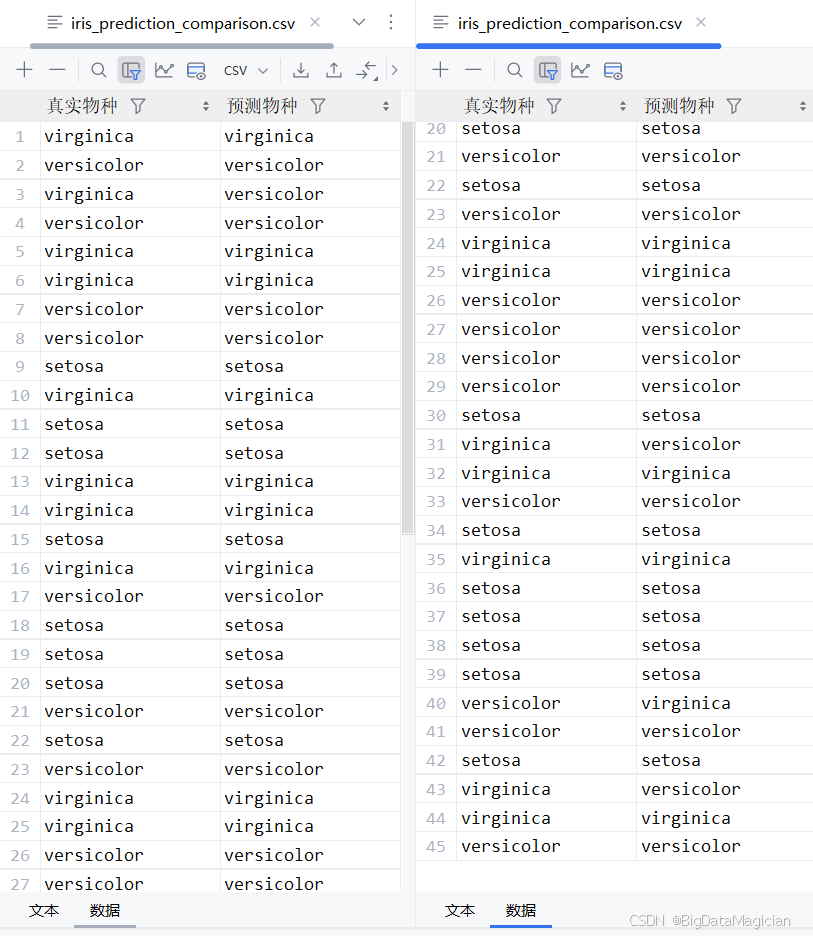
comparison_df.to_csv('iris_prediction_comparison.csv', index=False, encoding='utf-8-sig')

运行结果如下图所示，生成的对比表显示了每条测试样本的真实物种与模型预测结果。从结果图中可以看出，大部分样本的预测值与真实值一致，仅少数存在偏差，表明模型具备较强的分类能力。例如，setosa 类别几乎全部正确识别，说明该类特征明显、易于区分；而 versicolor 与 virginica 之间偶有误判，可能由于两者在花瓣长度等维度上存在重叠区域，导致分类边界不够清晰。整体来看，该模型在鸢尾花分类任务中表现稳定，具有较高的准确率和实用性。

5.2 预测类别概率

在分类任务中，除了输出最终的预测类别外，了解模型对每个类别的置信度同样重要。通过 model.predict_proba() 方法，可以获取测试集中每个样本属于各个类别的概率分布，这些概率值总和为1，能够直观反映模型在做出决策时的不确定性程度。例如，当某样本被预测为"virginica"且其对应概率接近1时，说明模型对该预测非常有信心；反之，若多个类别的概率相近，则表明模型存在犹豫或数据边界模糊。

python 复制代码

# 预测测试集每个样本的类别概率
y_pred_proba = model.predict_proba(X_test)

# 将概率数组转换为 DataFrame，列名为类别名称
prob_df = pd.DataFrame(y_pred_proba, columns=target_names)

# 添加真实标签和预测标签以便对照
prob_df.insert(0, '真实物种', y_test_names)
prob_df.insert(1, '预测物种', y_pred_names)

# 保留4位小数以提高可读性
prob_df = prob_df.round(4)

# 保存为 CSV 文件
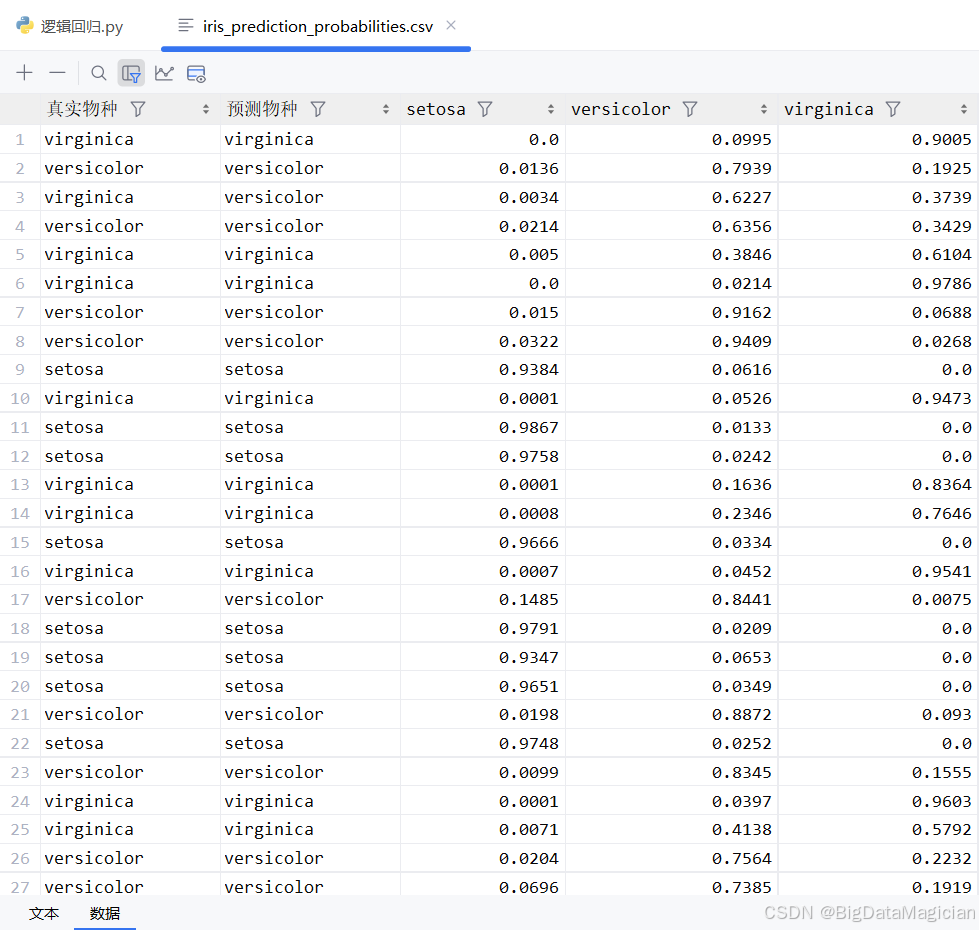
prob_df.to_csv('iris_prediction_probabilities.csv', index=False, encoding='utf-8-sig')

运行结果如下图所示，从图中可以看出，大多数样本的最高概率集中在正确类别上，且数值较高（如超过0.9），说明模型具有较强的判别能力。例如，setosa 类型的样本几乎全部在该列的概率接近1，而其他两类概率极低，体现了其与其他种类之间明显的特征差异。而对于少数误判样本（如第3行将 versicolor 预测为 virginica），其概率分布显示两者概率较为接近（分别为0.6227和0.3739），表明模型在此处存在一定困惑，这与两类在花瓣尺寸上的重叠特性一致。整体来看，概率输出不仅增强了模型的可解释性，也为后续风险评估和阈值调整提供了有力支持。

6. 模型评估

6.1 核心评估指标计算

在模型训练完成后，需通过科学的评估指标全面衡量其分类性能。本节采用准确率（Accuracy）作为整体性能的度量，并结合精确率（Precision）、召回率（Recall）和 F1 分数对每个类别进行细致分析。准确率反映所有样本中被正确分类的比例；精确率衡量预测为某类的样本中有多少是真正的该类；召回率表示真实属于某类的样本中有多少被成功识别；F1 分数则是精确率与召回率的调和平均，能综合反映模型在不平衡或边界模糊类别上的表现。这些指标共同构成了对分类器能力的多维度评估体系。

代码如下所示，首先调用 accuracy_score 函数计算测试集上的整体准确率，随后使用 classification_report 生成包含各类别精确率、召回率、F1 值和支持数（support）的详细报告。通过指定 target_names=target_names 参数，将原始数字标签（0/1/2）替换为可读的鸢尾花种类名称（如 'setosa'），并设置 digits=4 保留四位小数以提升结果精度和可读性。最终输出结构清晰、信息完整的评估结果，便于后续分析与决策。

python 复制代码

# 1. 准确率（整体分类正确的样本占比）
accuracy = accuracy_score(y_test, y_pred)
print(f"\n模型准确率：{accuracy:.4f}")

# 2. 详细分类报告（精确率、召回率、F1值）
print("\n详细分类报告：")
print(classification_report(
    y_test, y_pred,
    target_names=target_names,  # 显示类别名称
    digits=4  # 保留4位小数
))

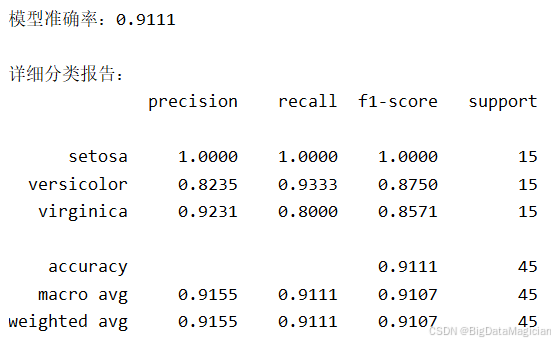
输入结果如下图所示，评估结果图显示模型整体准确率为 91.11%，表明绝大多数样本被正确分类。详细分类报告进一步揭示：setosa 类别在所有指标上均达到 1.0000，说明其特征显著、易于区分；而 versicolor 和 virginica 之间存在少量混淆------前者召回率高但精确率略低，后者则相反，反映出两者在花瓣长度和宽度等特征上存在重叠区域。宏平均（macro avg）和加权平均（weighted avg）的 F1 值均接近 0.91，说明模型在各类别间表现均衡，具备良好的泛化能力和实用价值。

7. 结果可视化

7.1 混淆矩阵可视化

混淆矩阵是分类模型评估中极为重要的可视化工具，能够直观展示模型在各类别上的预测表现。通过将真实类别与预测类别进行交叉对比，可以清晰识别出哪些类别被正确分类，哪些存在误判。

实现代码如下所示，首先调用 confusion_matrix 函数计算测试集的真实标签与预测标签之间的混淆矩阵，随后使用 seaborn.heatmap 进行可视化。为支持中文显示，设置了 plt.rcParams['font.sans-serif'] = ['SimHei'] 并关闭负号Unicode渲染（axes.unicode_minus=False）。热力图参数包括：annot=True 显示具体数值，cmap='Blues' 使用蓝色调渐变增强可读性，xticklabels 和 yticklabels 设置为类别名称以提升语义清晰度。最后通过 plt.savefig() 将图像保存为 PNG 文件，便于后续报告或分享使用。

python 复制代码

# 计算混淆矩阵
cm = confusion_matrix(y_test, y_pred)

# 可视化混淆矩阵
plt.figure(figsize=(6, 5))
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
sns.heatmap(
    data=cm,
    annot=True,  # 显示具体数值
    # fmt='d',  # 数值格式为整数
    cmap='Blues',
    xticklabels=target_names,
    yticklabels=target_names
)
plt.xlabel('预测类别')
plt.ylabel('真实类别')
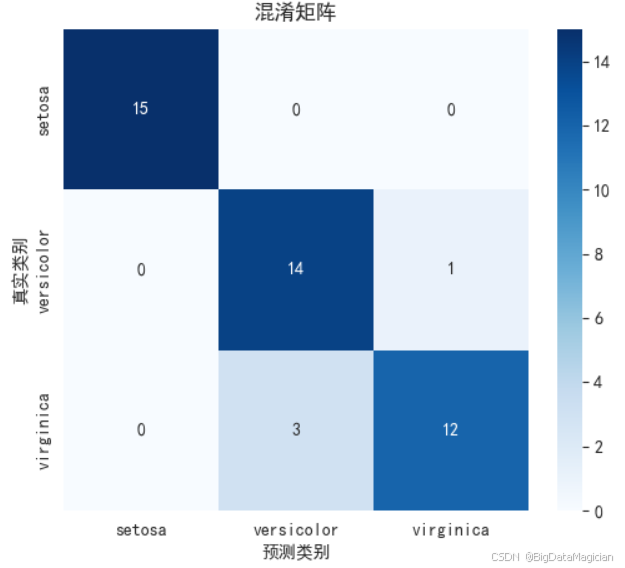
plt.title('混淆矩阵')
plt.savefig('iris_confusion_matrix.png')

运行结果如下图所示，以热力图形式呈现鸢尾花分类任务的混淆矩阵：行表示真实类别，列表示预测类别，每个格子中的数值表示对应类别的样本数量。颜色深浅反映预测准确度，越深表示数量越多。从图中可以看出，setosa 类完全正确分类（15/15），而 versicolor 和 virginica 之间存在少量混淆，说明模型在区分这两类时仍有一定挑战。

7.2 多分类ROC曲线与AUC

在多分类问题中，ROC曲线和AUC（曲线下面积）是衡量模型区分能力的重要指标。由于原始标签为多类别，需将其转换为 one-hot 编码形式（即二值化），以便对每个类别独立计算 ROC 曲线。每条曲线反映模型将某一类别与其他所有类别区分开来的性能：真正例率（TPR）越高、假正例率（FPR）越低，说明该类别的判别效果越好。AUC 值越接近 1，表示模型对该类的识别能力越强；若 AUC 接近 0.5，则表明模型表现接近随机猜测。通过绘制所有类别的 ROC 曲线，可全面评估模型在各类别上的整体判别性能。

实现代码如下，首先使用 label_binarize 将测试集的真实标签转换为 one-hot 格式，得到每个类别对应的二值标签矩阵。接着，遍历每个类别，调用 roc_curve 计算其 FPR 和 TPR，并利用 auc 函数计算曲线下面积。绘图时，为每条 ROC 曲线分配不同颜色并添加半透明填充（fill_between），增强可视化效果。同时绘制一条对角虚线作为随机猜测基准（AUC=0.5），便于对比。最终设置坐标轴标签、标题、图例，并保存图像，完整呈现多分类任务下的模型性能分析。

python 复制代码

# 1. 将多分类标签二值化（one-hot格式）
y_test_binarized = label_binarize(y_test, classes=[0, 1, 2])
n_classes = y_test_binarized.shape[1]

# 2. 计算每个类别的ROC曲线和AUC
plt.figure(figsize=(8, 6))
colors = ['blue', 'green', 'red']
for i in range(n_classes):
    # 计算FPR（假正例率）和TPR（真正例率）
    fpr, tpr, _ = roc_curve(y_test_binarized[:, i], y_pred_proba[:, i])
    # 计算AUC（曲线下面积，越接近1越好）
    roc_auc = auc(fpr, tpr)
    # 绘制ROC曲线
    plt.plot(
        fpr, tpr, lw=2, color=colors[i],
        label=f'{target_names[i]} (AUC = {roc_auc:.4f})'
    )
    plt.fill_between(fpr, tpr, alpha=0.2, color=colors[i])

# 添加随机猜测基准线（AUC=0.5）
plt.plot([0, 1], [0, 1], 'k--', lw=2)
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('假正例率（FPR）')
plt.ylabel('真正例率（TPR）')
plt.title('多分类ROC曲线')
plt.legend(loc='lower right')
plt.savefig('iris_roc_curve.png')

运行结果如下图所示，结果图展示了三个鸢尾花种类的 ROC 曲线：setosa 的 AUC 达到 1.0000，且曲线紧贴左上角，表明模型能完美区分该类别；versicolor 和 virginica 的 AUC 分别为 0.9933，曲线也极度靠近理想位置，说明模型在这两类上的区分能力极强，仅有极少数样本存在混淆。所有曲线均显著高于随机基准线，证明模型具有出色的分类判别能力。填充区域直观地体现了各 AUC 面积大小，进一步验证了模型在多分类任务中的高精度表现。

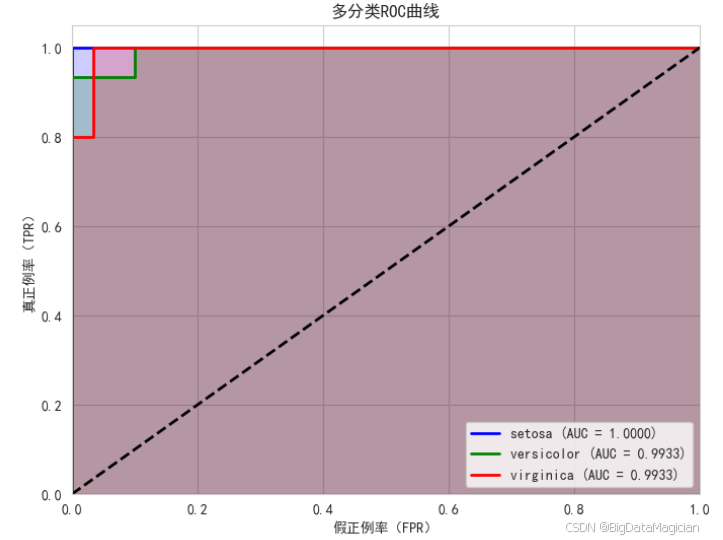
7.3 特征权重可视化

在逻辑回归模型中，每个特征的系数（即权重）反映了其对各类别预测结果的影响程度和方向。正系数表示该特征值越大，越倾向于预测为对应类别；负系数则相反。通过将这些权重以热力图形式可视化，可以直观地比较不同特征在区分各类别时的作用强弱与方向。本图展示了四个花瓣和萼片特征（sepal length, sepal width, petal length, petal width）在预测三种鸢尾花类别（setosa、versicolor、virginica）时的权重分布，帮助理解哪些特征是关键判别依据。

实现代码如下所示，首先从模型参数 DataFrame 中移除"截距"列，仅保留四个输入特征对应的系数，构建 coef_df 数据框。随后使用 seaborn.heatmap 绘制热力图：cmap='RdBu_r' 采用红蓝双色渐变，其中红色代表正权重（促进分类），蓝色代表负权重（抑制分类）；center=0 确保颜色以零为中心对称；annot=True 显示具体数值，fmt='.2f' 控制小数点后两位。最终添加标题并保存图像，生成清晰、可解释性强的特征权重可视化结果。

python 复制代码

# 构建特征权重DataFrame
coef_df = param_df.drop(columns=['截距'])

# 可视化特征权重（热力图）
plt.figure(figsize=(8, 6))
sns.heatmap(
    coef_df,
    annot=True,
    cmap='RdBu_r',
    center=0,
    fmt='.2f'
)
plt.title('各特征对类别预测的权重')
plt.savefig('iris_feature_weights.png')

运行结果如下图所示，热力图显示了各特征在三类预测中的权重情况：对于 setosa，petal length 和 petal width 权重为显著负值（-1.67、-1.59），说明其花瓣较短小是识别 setosa 的关键特征；而 sepal width 为正值（0.94），表明宽萼片也有助于识别该类。virginica 类中，petal length 和 petal width 权重极高（1.80、2.39），呈深红色，说明大花瓣是其最显著的判别特征。versicolor 的权重普遍较小，反映其特征与其他两类存在重叠。整体来看，花瓣尺寸是区分三类的核心依据，而萼片特征作用相对次要。

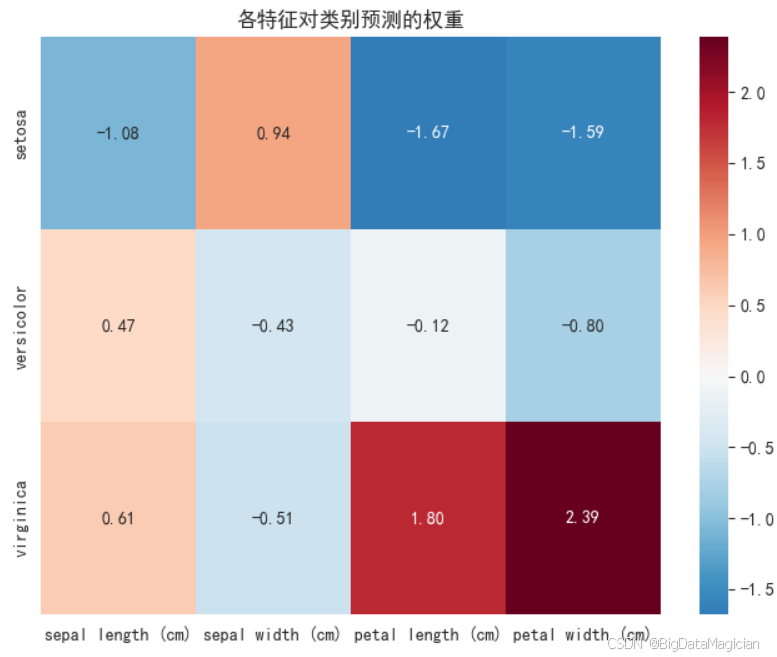
8. 模型解释

逻辑回归模型的参数（截距和特征权重）具有明确的物理意义，可通过分析这些参数解释模型的决策逻辑，即"哪些特征对分类结果影响更大""特征如何影响类别预测"。以下结合鸢尾花数据集的模型参数展开具体解释：

8.1 模型参数回顾

首先回顾前文得到的模型参数DataFrame（截距+特征权重），以典型结果为例：

类别	截距	花萼长度(cm)	花萼宽度(cm)	花瓣长度(cm)	花瓣宽度(cm)
setosa	11.3272	-0.4236	0.9604	-2.5177	-1.0824
versicolor	-1.7108	0.5340	-0.3151	-0.2061	-0.6441
virginica	-9.6164	-0.1104	-0.6453	2.7238	1.7265

8.2 特征权重的物理意义

逻辑回归通过 sigmoid函数 将线性组合结果映射为概率，对于多分类（多项式逻辑回归），每个类别的预测概率可表示为：
P ( y = k ∣ X ) = e β k 0 + β k 1 x 1 + . . . + β k 4 x 4 ∑ i = 0 2 e β i 0 + β i 1 x 1 + . . . + β i 4 x 4 P(y=k|X) = \frac{e^{\beta_{k0} + \beta_{k1}x_1 + ... + \beta_{k4}x_4}}{\sum_{i=0}^{2} e^{\beta_{i0} + \beta_{i1}x_1 + ... + \beta_{i4}x_4}} P(y=k∣X)=∑i=02eβi0+βi1x1+...+βi4x4eβk0+βk1x1+...+βk4x4

其中， β k 0 \beta_{k0} βk0 为类别 k k k的截距， β k 1 . . . β k 4 \beta_{k1}...\beta_{k4} βk1...βk4 为特征权重。

权重符号：
- 正值：特征值增大时，该类别的预测概率升高（促进作用）。
- 负值：特征值增大时，该类别的预测概率降低（抑制作用）。
权重绝对值：绝对值越大，特征对该类别的影响越强。

8.3 分类别解释模型决策逻辑

8.3.1 山鸢尾（setosa）

截距（11.3272）：在所有特征为0时，setosa的基础概率远高于其他类别（截距为三者最大），说明模型倾向于优先判断样本为setosa（除非其他特征强烈反对）。
关键特征影响 ：
- 花瓣长度（-2.5177）：权重绝对值最大且为负，是区分setosa的核心特征------花瓣长度越小（如1-2cm），setosa的概率越高（与EDA中setosa花瓣最短的规律一致）。
- 花萼宽度（0.9604）：唯一的正向权重，花萼宽度越大（如3-4cm），越可能是setosa（符合EDA中setosa花萼较宽的特点）。
- 花萼长度（-0.4236）和花瓣宽度（-1.0824）：均为负值，说明花萼越长、花瓣越宽，setosa的概率越低。

8.3.2 变色鸢尾（versicolor）

截距（-1.7108）：基础概率低于setosa，但高于virginica，说明模型对versicolor的"初始倾向"中等。
关键特征影响 ：
- 花萼长度（0.5340）：唯一的正向权重，花萼越长（如5-6cm），versicolor的概率略高。
- 其他特征（花萼宽度、花瓣长度、花瓣宽度）均为负值：说明这些特征增大时，versicolor的概率会被抑制（例如花瓣过长更可能是virginica，花瓣过短更可能是setosa）。

8.3.3 维吉尼亚鸢尾（virginica）

截距（-9.6164）：基础概率最低，说明模型需要较强的特征信号才会判断样本为virginica。
关键特征影响 ：
- 花瓣长度（2.7238）：权重绝对值最大且为正，是区分virginica的核心特征------花瓣长度越大（如5-7cm），virginica的概率越高（与EDA中virginica花瓣最长的规律一致）。
- 花瓣宽度（1.7265）：正向权重，花瓣越宽（如1.5-2.5cm），越可能是virginica。
- 花萼宽度（-0.6453）：负值，花萼宽度越大，virginica的概率越低（因setosa花萼更宽）。

8.4 核心结论

特征重要性排序 ：

花瓣长度是区分三类鸢尾花的最关键特征（权重绝对值最大），其次是花瓣宽度和花萼宽度，花萼长度的影响较弱。
分类逻辑总结：
- 花瓣长度≤2cm → 极可能是setosa；
- 2cm＜花瓣长度＜5cm → 倾向于versicolor；
- 花瓣长度≥5cm → 极可能是virginica。
  （该规律与EDA中特征分布一致，验证了模型的合理性）。
模型局限性 ：

当花瓣长度在4-5cm区间（versicolor与virginica重叠区域），模型可能因特征信号模糊而误判，这与混淆矩阵中少量错误分类的结果一致。

通过模型解释，不仅能理解逻辑回归"如何做出预测"，还能验证模型是否符合业务常识（如鸢尾花的形态学规律），为模型的可信度提供支撑。