图论基础概念
对于图论算法,目前不要求会实现复杂算法,但手工操作还是要会的。
什么是图
一个图是一个序偶 <V, E>(序偶:由两组有序元素组合的二元组),记为 G =<V, E> 。
V 为顶点集, E 为 V 中结点之间的边的集合。
自环: 一条边的两个端点是相同的。
重边: 两个端点之间有两条以上的边,称他们是重边。
简单图: 没有自环和重边的图。
无向边: 边是双向的。
有向边: 单向边,有箭头。
无向图: 只有无向边的图。
有向图: 只有有向边的图。
混合图: 既有无向边又有有向边。
顶点的度: 无向图中,一个顶点相连的边数称为该顶点的度;有向图中,从一个顶点出发的边数称为该顶点得出度;到达该顶点的边数称为它的入度。
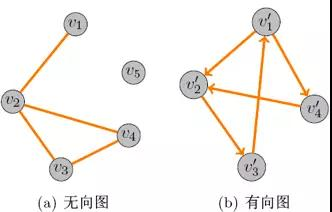
图论基本定理: 著名的握手定理。无向图中结点度数的总和等于边数的两倍。有向图中结点入度的和等于出度的和等于边数。
通路: 给定图G中结点和边交替出现的一个序列:v0 e1 v1 e2 v2 ... ek vk,若每条边ei的两端点是vi-1 和vi ,那么称该序列是从v0到vk的一条通路。
基本通路(路径): 没有重复出现的结点的通路。
图的连通性: 若一张无向图的任意两个结点之间都存在通路,那么称该图是连通的。
连通分量: 图中连通的顶点与边的集合(即若干个点直接可以相互连通,那么它们共同组成一个连通分量)。
权和网: 在图的边给出相关的数,成为权。权可以表示一个顶点到另一个顶点的距离,耗费等。带权图一般成为网。
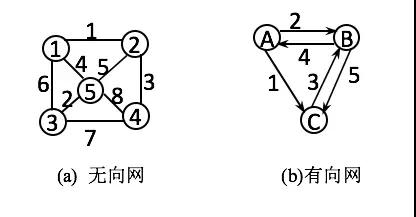
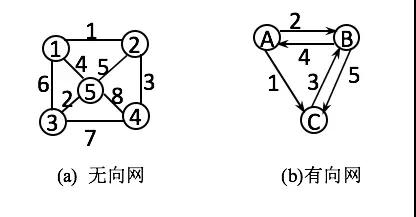
最短路径: 对于一张不带权的无向图来说,从s到t的最短路径就是所有从s到t的通路中长度最短的那一条(可能不唯一),通路上的边数称为路径的长度。
完全图: 任何两个顶点之间都有边(弧)相连称为完全图。
稀疏图、稠密图: 边(弧)很少的图称为稀疏图,反之为稠密图。
图的存储:邻接矩阵
在邻接矩阵表示中,除了存放顶点本身信息外,还用一个矩阵表示各个顶点之间的关系。若(i,j)∈E(G)或〈i,j〉∈E(G),则矩阵中第i行 第j列元素值为1,否则为0 。
例如, 下面为两个无向图和有向图对应的邻接矩阵。
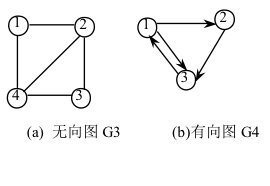
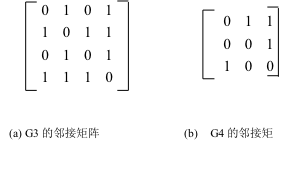

空间复杂度:O(V^2)
优点:直观,容易理解,可以直接查看任意两点的关系。
缺点:对于稀疏图,会有很多空间根本没有利用。对于带权图,不能处理重边。要查询某一个顶点的所有边,要枚举V次。
图的存储:邻接表
对图的每个顶点建立一个单链表(n个顶点建立n个单链表),第i个单链表中的结点包含顶点Vi的所有邻接顶点。
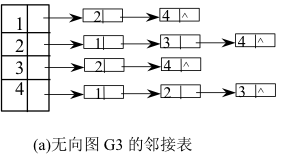
空间复杂度:有向图O(V+E)无向图O(V+2*E)
优点:节省空间,能快速找到某个顶点所有相连的顶点,而无需访问无关顶点。
图的遍历
为什么要遍历?很多图上的信息只通过点与边的集合是很难获得的,通过对图的遍历我们可以获取图上的信息。
图的遍历算法:宽度优先遍历(BFS)
给定图G和一个源点s, 宽度优先遍历按照从近到远的顺序考虑各条边. 算法求出从s到各点的距离。
宽度优先的过程将点分为两种:已经走过的点和没走过的点。
每次选择队头的点向周围进行搜索,并将所有没入过队的点入队。