此分类用于记录吴恩达深度学习课程的学习笔记。
课程相关信息链接如下:
- 原课程视频链接:[双语字幕]吴恩达深度学习deeplearning.ai
- github课程资料,含课件与笔记:吴恩达深度学习教学资料
- 课程配套练习(中英)与答案:吴恩达深度学习课后习题与答案
本篇为第二课的第二周内容,2.6的内容。
本周为第二课的第二周内容,和题目一样,本周的重点是优化算法,即如何更好,更高效地更新参数帮助拟合的算法,还是离不开那句话:优化的本质是数学 。
因此,在理解上,本周的难道要相对较高一些,公式的出现也会更加频繁。
当然,我仍会补充一些更基础的内容来让理解的过程更丝滑一些。
本篇的内容关于Momentum梯度下降法(动量梯度下降法),是应用了上一篇指数加权平均逻辑的梯度下降法。
1. Momentum 梯度下降法
1.1梯度下降中的"震荡"现象
我们用课程里的图来看一下这个问题:
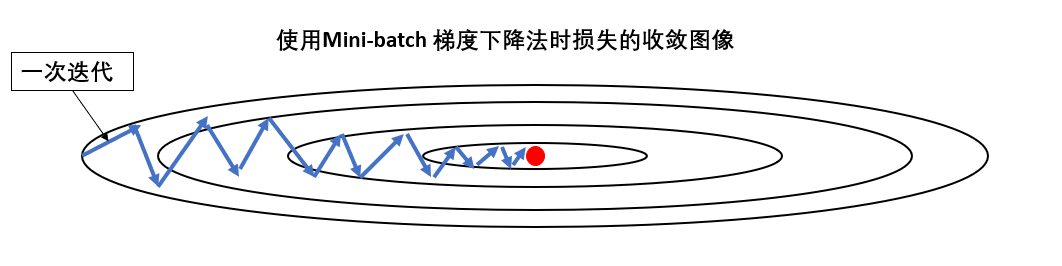
现在假设这就是我们的网络的损失图像,我们通过一次次迭代,让损失下降到最低点。
这里展开两个问题:
(1)为什么迭代过程会让损失上下震荡?
因为每个批次的样本不可能完全相同,不同的特征倾向会指引参数向不同的方向更新。
甚至如果一个批次中大多是噪声,反而会让参数反向更新,增加损失。
就像猫狗分类中,一个批次可能白猫多一些,一个批次可能橘猫多一些,而还有一些批次甚至有和狗长得很像的猫,这都会影响该次迭代中的学习效果,从而影响参数更新,而这前后的不同就会让损失"震荡"。
(2)为什么不改变学习率震荡也会越来越小?
因为在收敛的过程中,损失函数变平坦 ,梯度变小,更新步长随之减小。
同时,样本间的梯度差异(噪声)也随之变小,使震荡幅度下降。
来看一下参数更新公式:
\[参数 := 参数 - 学习率*梯度 \]
在学习率不变的情况下梯度越来越小了,自然更新量就会变小,影响损失的变化量也会变小。
依旧用下山举例:就像越靠近山谷底部,地面越平坦,即使走偏一步,你也走不上多高的坡,自然"来回晃动"的幅度越来越小。
但这只是理想情况,如果学习率设置不当,就会出现这中情况:
- 你快到谷底了,却还在大步流星,根本刹不住车,一脚又上了另一座山。
- 你走得太慢了,甚至可能在谷底附近的浅坑里转圈圈,迟迟到不了真正的低点
而且,说到底,震荡现象依然存在,只是在收敛中随着整体移动量变小而没那么明显了,如何解决这种情况,又不影响正常收敛呢?
1.2 解决震荡的直接方法
通过上面一部分,我们现在已经知道了,出现震荡的本质原因是批次训练中样本的差异导致的单次迭代的结果差异。
那么你可能已经猜到了一个解决这个问题的最直接的方法:增加批次样本量
没错,只要我们增加批次样本量,模型一次学习更多的样本,自然就学到了更多的特征分布,出现"噪声集中"的几率也会变少。
就像刚刚的猫狗分类里,原来模型看完白猫就学白猫,然后看橘猫学橘猫,之后再看"狗猫"学"狗猫",就像对什么都很好奇的小孩,每遇到新的一批样本,都要调整自己对猫的认知,就是一次震荡。
现在我把黑白红蓝猫一次让模型看完,模型就知道这些颜色的猫都是猫了,就像见识广了的成年人,遇到新样本发现其实里面的特征自己之前已经见过了,自然不会有那么多的震荡。
可是这样就又出现新问题了,在本周第一部分里我们就已经论述了选择Mini-batch梯度下降是成本和性能的权衡考虑 ,如果不计其他因素地增加批次样本,那不就是批次梯度下降,即一次就使用所有样本来训练吗?
这会带来:
- 显存暴涨
- 单步计算量巨增
- 训练速度不一定更快
- 大 batch 收敛容易"卡平坦鞍点"
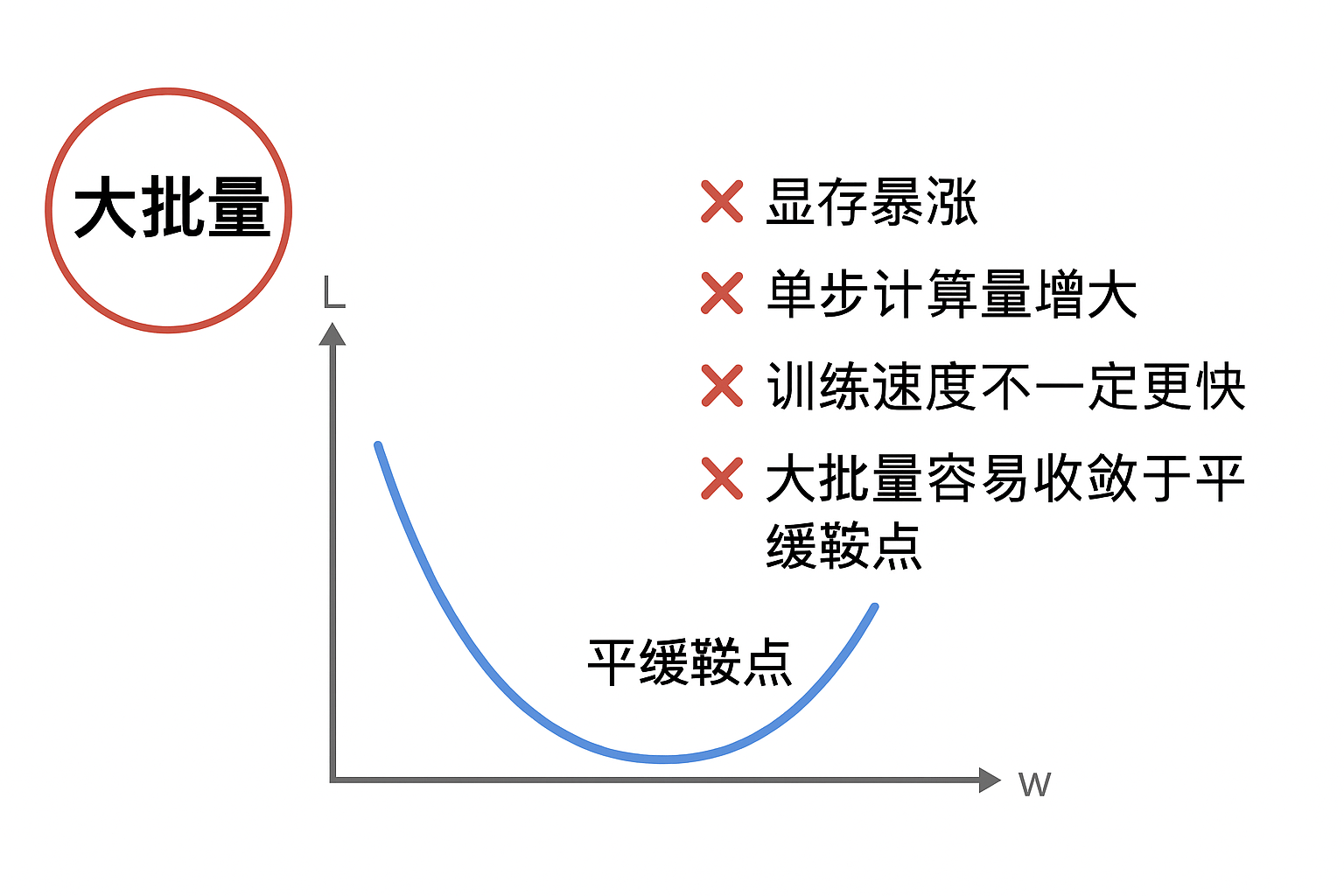
因此,Batch 不是越大越好,而是追求成本与梯度稳定之间的平衡。
而这也引出了一个核心动机:我们希望在小 batch 的成本下,获得"大 batch 才有的稳定梯度效果"。
这正是 Momentum 要解决的。
1.3 Momentum 梯度下降法
我们已经通过气温的例子学习了指数加权平均的概念。
回忆一下气温的例子:
每天的气温都有波动,直接看"当天温度",得到的曲线会忽高忽低、不够平滑,就像"震荡"。
但如果对气温做 EMA,今天的气温占 70%,昨天占 21%,前天占 6%...那得到的温度曲线就会 更平滑、更稳定、更能代表真实趋势。
再看看我们现在要解决的震荡问题,它的核心在于每次更新只依赖该批次样本计算的梯度 。
现在的更新方式是不是就相当于"当天温度"?
那是不是同理,只要我们对梯度进行EMA,让一次迭代不只依赖本次样本计算的梯度,而是多批次样本梯度的指数加权平均,是不是就相当于变相地增加了批次样本量?
我们再换个角度加深一下理解,再次回看这副图:
先强调一下,真实的图像和方向代表的信息要远比图里的复杂的多,我们只是简化来帮助理解。
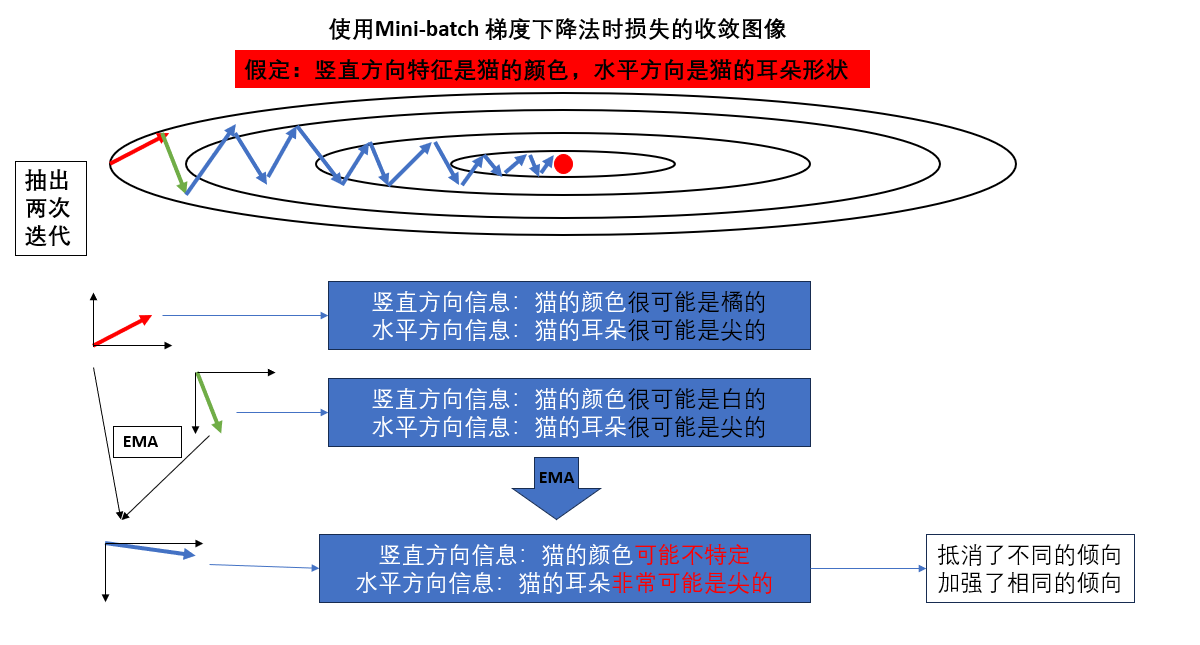
就像图里画的一样,我们抽出其中两次迭代,并假定他们所代表的特征。
这样,如果第二次迭代使用的是EMA梯度,那它就得到了更平衡,更指向核心特征的信息。
就像把每个人自己独特的观点综合考量,而每个人都赞同的观点那大概是对的,就大力采纳。
而这就是Momentum 梯度下降法的核心观点:
- 对多次计算的梯度做EMA,用EMA来更新参数。
- 如果梯度方向总是在某个方向上保持一致,那我们就应该越走越快。
- 如果梯度方向来回变化,就不要轻易被改变。
其公式如下:
记参数为 \(\theta\),梯度为 \(g_t = \nabla_\theta J(\theta)\),动量项为 \(v_t\),动量系数为 \(\beta \in [0,1)\),学习率为 \(\eta\),则
\[v_t = \beta v_{t-1} + (1 - \beta) g_t \]
\[\theta_t = \theta_{t-1} - \eta v_t \]
其中,\(v_t\)相当于累积了之前多次梯度的"指数加权平均":
- 当梯度方向稳定时,\(v_t\) 会越来越大,加快下降速度。
- 当梯度方向来回变化时,\(v_t\) 会相互抵消,减少震荡。
这样,我们使用Momentum 梯度下降法,用指数加权平均后的梯度更新参数,既增加了核心特征上的收敛速度,又缓解了非个性化特征带来的震荡现象。
2."人话版"总结
| 概念 | 原理 | 比喻 |
|---|---|---|
| 梯度下降中的震荡 | 每个批次样本不同,导致每次迭代的梯度方向不一致,参数更新"来回晃动"。 | 就像走山路,有时被小石头绊偏,走两步又回到原路,来回摇摆。 |
| 学习率不变时震荡减小 | 随着收敛,损失函数变平坦,梯度变小,更新步长减小,自然震荡幅度下降。 | 越靠近山谷底部,地面平坦,即使走偏也不会翻到对面山坡。 |
| 增大批次(解决震荡直接方法) | 一次学习更多样本,梯度更稳定,噪声影响减小。 | 小孩学猫时只看一种颜色的猫,会不断调整认知;一次看多种颜色的猫,就稳了。 |
| Momentum 梯度下降法 | 对多次迭代的梯度做指数加权平均(EMA),用EMA更新参数;稳定方向加速,震荡方向抵消。 | 就像综合多个人的意见:大多数人一致的方向就加速采纳,意见分歧的方向就减缓。 |
| Momentum 梯度下降法公式 | \((v_t = \beta v_{t-1} + (1-\beta) g_t),(\theta_t = \theta_{t-1} - \eta v_t)\) | EMA累积前几次梯度,相当于"记住过去的方向",走路更稳、更快。 |