计算机视觉（三）：特征检测与光流法

12.彩色视觉

首先介绍彩色成像技术 的四种实现方式（场时序 、多芯片 、色彩滤镜阵列 如Bayer模式、Foveon X3传感器 ，其中Foveon X3通过三层CMOS实现每个像素捕捉RGB三通道）；其次阐述颜色基础，包括电磁波光谱 （可见光400-700nm）、加性颜色混合 （RGB混合成白光，适用于显示器）与减性颜色混合 （CMY混合成黑色，适用于印刷）；接着讲解颜色匹配实验 （通过调整三原色权重匹配测试光，推导颜色匹配函数）及标准颜色空间 （线性空间如RGB、CIE XYZ，非线性空间如CIE LAB（感知均匀）、HSV（直观调色））；最后介绍环境对颜色感知的影响（色适应 、同化作用、后像）及颜色的实际应用（基于颜色的图像检索（CBIR）、皮肤检测、目标跟踪），并布置作业要求用C/C++实现皮肤检测算法。

---

思维导图

---

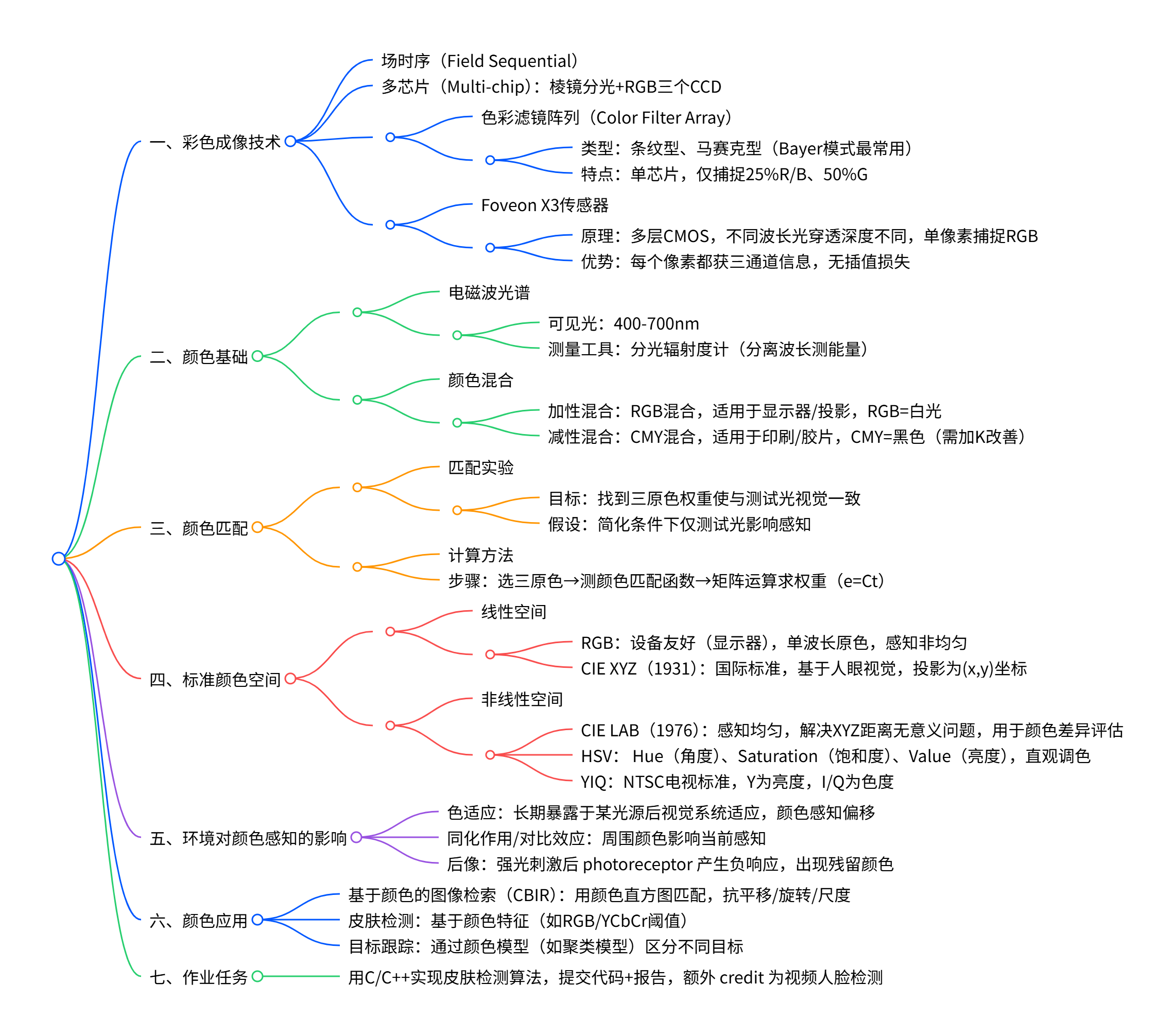
详细总结

彩色成像技术

彩色成像通过不同硬件方案实现RGB三通道信息捕捉，四种核心技术对比如下：

技术类型	核心原理	关键特点	应用场景
场时序（Field Sequential）	按时间顺序切换RGB光源/滤镜，单传感器分时捕捉	结构简单，易出现色彩串扰	早期彩色相机
多芯片（Multi-chip）	镜头→棱镜分光（按波长）→RGB三个CCD分别接收	色彩还原准，无插值，体积大、成本高	专业摄影设备（如单反）
色彩滤镜阵列（CFA）	单芯片表面覆盖RGB滤镜马赛克（如Bayer模式）	常用Bayer模式（2G:1R:1B），仅25%R/B、50%G	消费级相机、手机摄像头
Foveon X3传感器	三层CMOS传感器，不同波长光穿透深度不同（红深、绿中、蓝浅）	每个像素直接捕捉RGB三通道，无插值损失	专业级相机（如Sigma相机）

光谱与颜色混合

1. 光谱基础

   • 电磁波光谱中可见光范围400-700nm ，测量工具为分光辐射度计（分离波长并测量各波长能量）；
   • 光源光谱示例：红宝石激光（单波长）、钨丝灯（连续光谱）、日光（宽光谱）。

2. 颜色混合类型

混合类型	核心原理	原色组合	混合结果	应用场景
加性混合	不同波长光叠加，能量相加	R（红）、G（绿）、B（蓝）	RGB叠加产生白光，R+G=黄，G+B=青，R+B=品红	显示器、投影仪、LED屏幕等发光设备
减性混合	颜料吸收特定波长，反射剩余波长，能量相减	C（青）、M（品红）、Y（黄）	CMY理论上叠加为黑色，实际需加K（黑）增强	印刷、胶片、颜料调色等吸光介质

颜色匹配

1. 颜色匹配实验

   • 目标：确定三原色（ primaries ）的权重，使与测试光的视觉效果一致；
   • 实验设计：双分区屏幕，一侧为测试光，另一侧为可调强度的三原色，观察者调整权重至视觉匹配；
   • 关键现象：部分测试光需"负权重"（将某原色加入测试光侧才能匹配）。

2. 颜色匹配计算

   • 步骤1：选择三原色（如645.2nm红、525.3nm绿、444.4nm蓝）；
   • 步骤2：测量颜色匹配函数 c1(λi),c2(λi),c3(λi)c_1(\lambda_i),c_2(\lambda_i),c_3(\lambda_i)c1(λi),c2(λi),c3(λi)（单位波长测试光的三原色权重）；
   • 步骤3：对任意光谱信号t(λ)t(\lambda)t(λ)，通过矩阵运算求权重：[e1e2e3]=[c1(λ1)⋯c1(λN)c2(λ1)⋯c2(λN)c3(λ1)⋯c3(λN)][t(λ1)⋮t(λN)]\begin{bmatrix}e_1\\e_2\\e_3\end{bmatrix}=\begin{bmatrix}c_1(\lambda_1)&\cdots&c_1(\lambda_N)\\c_2(\lambda_1)&\cdots&c_2(\lambda_N)\\c_3(\lambda_1)&\cdots&c_3(\lambda_N)\end{bmatrix}\begin{bmatrix}t(\lambda_1)\\\vdots\\t(\lambda_N)\end{bmatrix} e1e2e3 = c1(λ1)c2(λ1)c3(λ1)⋯⋯⋯c1(λN)c2(λN)c3(λN) t(λ1)⋮t(λN) ，即e=Cte=Cte=Ct。

标准颜色空间

颜色空间用于数值化表示颜色，分为线性与非线性两类，核心参数对比如下：

颜色空间	类型	核心特点	关键参数/标准	应用场景
RGB	线性	设备友好，基于单波长原色，感知非均匀	R(0-255)、G(0-255)、B(0-255)	显示器、相机、数字图像存储
CIE XYZ	线性	1931年CIE制定，基于人眼视觉，国际标准	X、Y、Z（三刺激值），投影(x=X/(X+Y+Z),y=Y/(X+Y+Z))	颜色标准化、跨设备转换
CIE LAB	非线性	1976年制定，感知均匀（相同距离对应相同视觉差异）	L（亮度）、a（红绿）、b（黄蓝）	颜色差异评估、印刷调色
HSV	非线性	直观符合人类调色习惯，H编码为角度	H(0-360°)、S(0-1)、V(0-1)	图像编辑（如PS调色）
YIQ	非线性	NTSC电视标准，分离亮度（Y）与色度（I/Q）	Y（亮度）、I（橙蓝）、Q（绿紫）	电视广播、视频压缩

• 关键补充：CIE XYZ存在感知非均匀 问题（相同坐标距离≠相同视觉差异），通过McAdam椭圆验证，因此需CIE LAB等均匀空间优化。

环境对颜色感知的影响

1. 色适应（Chromatic Adaptation）：长期暴露于某光源（如暖光、冷光），视觉系统会适应该光源的色度与亮度，导致相同物体在不同光源下感知颜色不同；
2. 同化作用与对比效应：周围颜色影响当前感知（如灰色块在红色背景下偏绿，在绿色背景下偏红）；
3. 后像（Afterimage）：强光刺激后，感光细胞产生负响应，出现与刺激色互补的残留图像（如长时间看红色后，看白色背景出现绿色后像）。

颜色的实际应用

1. 基于颜色的图像检索（CBIR）

   • 原理：提取图像颜色直方图（无空间信息，抗平移/旋转/尺度），计算查询图与数据库图的直方图交集，按相似度排序；
   • 示例：Google图片搜索、Spylight时尚检索。

2. 颜色基皮肤检测

   • 核心：利用皮肤在特定颜色空间（如YCbCr、RGB）的阈值范围，区分皮肤与非皮肤区域；
   • 应用：人脸检测、视频监控中的目标分割。

3. 颜色基目标跟踪

   • 原理：为每个目标建立颜色模型（如聚类模型），通过颜色匹配跟踪目标（如跟踪不同人物）；
   • 参考算法：D.Ramanan等人的"Tracking People by Learning their Appearance"。

作业任务

• 要求：用C/C++ 编写皮肤检测算法，提交代码+实验报告；
• 额外 credit：基于皮肤颜色在视频中实现人脸检测。

---

关键问题

彩色成像技术中，色彩滤镜阵列（如Bayer模式） 与Foveon X3传感器在RGB信息捕捉方式上有何核心差异？这些差异导致二者在图像质量与应用场景上有何不同？

核心差异体现在"RGB信息的像素级捕捉方式"：

1. 色彩滤镜阵列（Bayer模式）：

   • 捕捉方式：单芯片表面覆盖RGB滤镜马赛克，常用2G:1R:1B 比例（人眼对绿光更敏感），每个像素仅捕捉1个通道（如R或G或B），缺失通道需通过插值（如双线性插值）补充；
   • 图像质量：存在插值误差，易产生伪色或细节损失；
   • 应用场景：消费级设备（手机、普通相机），成本低、体积小。

2. Foveon X3传感器：

   • 捕捉方式：三层CMOS传感器，利用"不同波长光穿透硅的深度不同"（蓝光穿透浅、绿光中、红光深），每个像素直接捕捉RGB三通道信息，无需插值；
   • 图像质量：无插值损失，色彩还原更准、细节更丰富；
   • 应用场景：专业级设备（如Sigma单反相机），对色彩精度要求高的场景（专业摄影、色彩检测）。

加性颜色混合 与减性颜色混合的核心原理、原色组合及能量变化规律完全不同，试对比二者差异，并说明各自的典型应用场景为何不同？

二者差异源于"能量作用方式"，具体对比如下：

对比维度	加性颜色混合	减性颜色混合
核心原理	不同波长的光直接叠加，能量相加	颜料/滤光片吸收特定波长，反射剩余波长，能量相减
原色组合	R（红，650nm）、G（绿，550nm）、B（蓝，~450nm）	C（青）、M（品红）、Y（黄）（分别吸收R、G、B）
混合规律	原色叠加：RGB=白光，R+G=黄，G+B=青，R+B=品红	原色叠加：CMY=黑色（理论），实际因颜料纯度需加K（黑）
能量变化	混合后总能量≥单一原色能量（如R+G能量>R）	混合后总能量≤单一原色能量（如C+M反射能量<C）
应用场景差异	适用于"自发光设备"（显示器、投影仪、LED），因设备可直接发射RGB光叠加；	适用于"非自发光介质"（印刷、胶片、颜料），因介质需通过反射环境光呈现颜色，需用颜料吸收特定波长。

CIE XYZ颜色空间作为国际标准，为何还需要CIE LAB颜色空间？二者在"感知均匀性"上有何核心差异？CIE LAB的哪些设计使其能解决XYZ的不足？

答案：

1. 需CIE LAB的原因：CIE XYZ虽为国际标准，但存在感知非均匀性------坐标空间中"相同的欧氏距离"对应"不同的视觉颜色差异"，无法准确量化人眼感知的颜色相似度，而实际场景（如印刷调色、颜色质量检测）需"坐标距离与视觉差异成正比"，因此需CIE LAB优化。

2. 感知均匀性差异：

   • CIE XYZ ：非均匀，通过McAdam椭圆验证------在XYZ的(x,y)投影图中，人眼能分辨的最小颜色差异（Just Noticeable Difference, JND）表现为大小、形状不同的椭圆，椭圆越大，该区域坐标距离与视觉差异的偏差越大（如红色区域椭圆远大于绿色区域）；
   • CIE LAB：感知均匀，1976年基于XYZ转换而来，通过非线性变换调整坐标比例，使LAB空间中"相同的欧氏距离"对应"人眼感知的相同颜色差异"，McAdam椭圆近似为大小一致的圆。

3. CIE LAB的设计优化：

   • 坐标定义：L（亮度，0=黑~100=白）、a（红绿轴，a+为品红、a-为绿）、b（黄蓝轴，b+为黄、b-为蓝）；
   • 转换逻辑：基于XYZ与标准白光（如D65）的关系，通过非线性压缩（如对XYZ值取立方根）调整感知比例，确保不同颜色区域的视觉差异与坐标距离一致，满足颜色差异评估、跨设备颜色匹配等需求。

---

13.计算机视觉中的特征检测

核心聚焦点特征检测 ：首先定义特征为"不同图像间具有不变性的表示"，说明其在全景拼接 等场景中的关键作用（如通过"检测特征点→匹配→图像配准"实现拼接）；随后详细阐述Harris角点检测 （基于H矩阵的特征值分类角点/边缘/平坦区域，响应函数R=det(H)−αtrace(H)2R=det(H)-αtrace(H)^2R=det(H)−αtrace(H)2，α=0.06，具有旋转/光照不变性但无尺度不变性）；重点讲解SIFT（尺度不变特征变换） （Lowe 2004年提出，通过构建高斯金字塔与DoG尺度空间、极值检测、亚像素关键点定位、方向分配及128维描述子，实现旋转/尺度/光照不变性）；最后介绍特征检测的典型应用------全景拼接（完整流程：提取SIFT特征→k-d树匹配→RANSAC求单应→捆绑调整→光度融合），并提及Harris的ANMS改进（解决特征点分布不均问题）。

---

思维导图

---

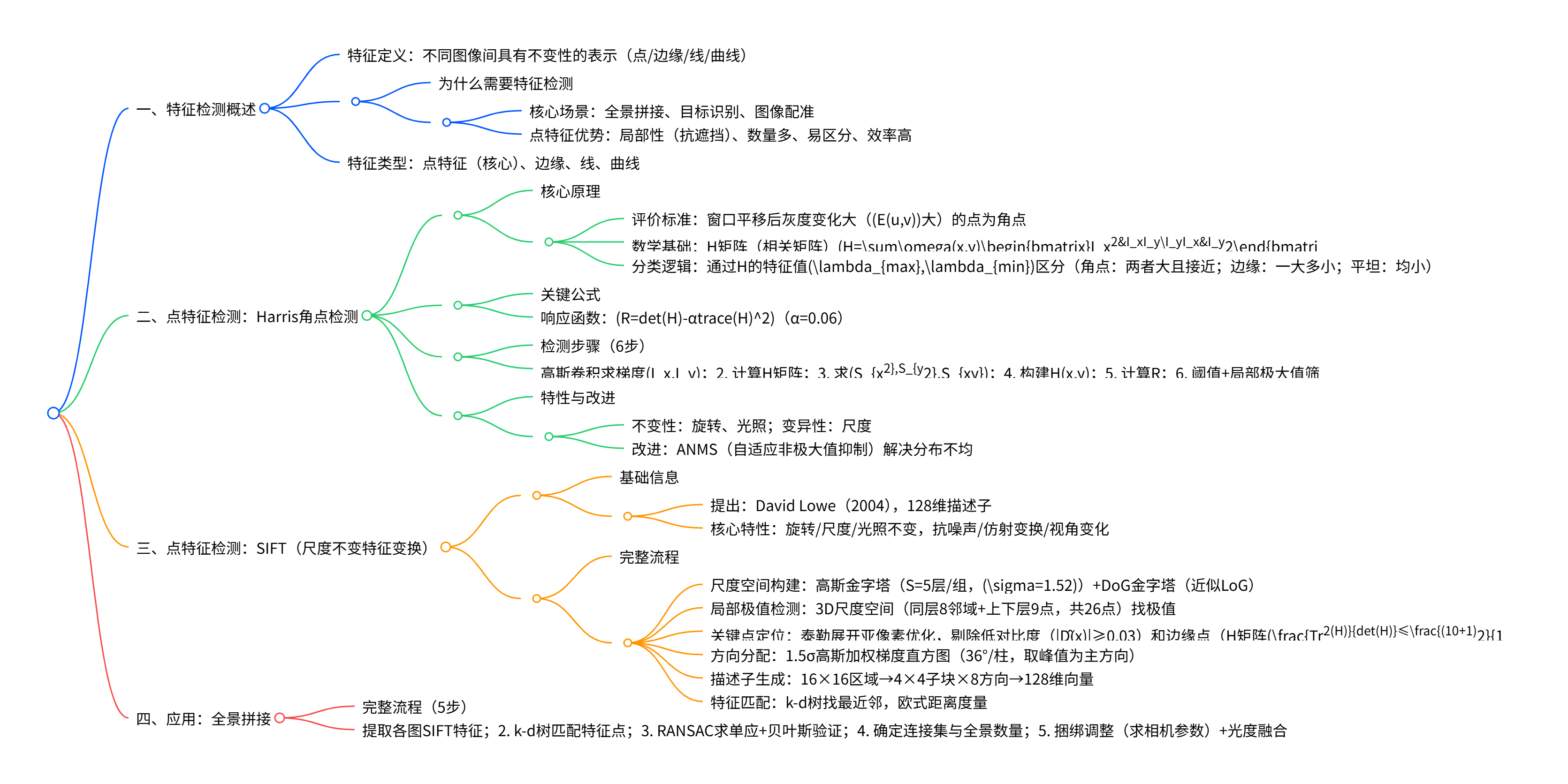
详细总结

特征检测基础

1. 特征的定义与意义

   • 特征：图像中"不同图像间具有不变性的表示"，需满足"外观相似性"，是实现图像配准、拼接、识别的核心。
   • 为什么需要特征检测：直接处理像素级数据计算量大，特征可压缩信息（如全景拼接需通过特征点匹配实现图像对齐）。
   • 特征类型 ：聚焦点特征（核心），此外还有边缘、线、曲线等，点特征因"局部性（抗遮挡）、数量多、易区分、效率高"成为主流。

2. 点特征的评价标准

   优质点特征需满足：窗口沿任意方向平移时，灰度变化显著

Harris角点检测（核心点特征算法1）

1. 数学原理

• 灰度变化度量 ：设窗口WWW平移(u,v)(u,v)(u,v)，加权平方差（SSD）为：
  E(u,v)=∑(x,y)∈Wω(x,y)[I(x+u,y+v)−I(x,y)]2E(u,v)=\sum_{(x,y)\in W}\omega(x,y)[I(x+u,y+v)-I(x,y)]^2E(u,v)=(x,y)∈W∑ω(x,y)[I(x+u,y+v)−I(x,y)]2
  其中ω(x,y)\omega(x,y)ω(x,y)为高斯窗口（加权邻域），III为灰度值。

• H矩阵（相关矩阵） ：对I(x+u,y+v)I(x+u,y+v)I(x+u,y+v)泰勒展开并化简，得E(u,v)≈[uv]H[uv]E(u,v)\approx\begin{bmatrix}u&v\end{bmatrix}H\begin{bmatrix}u\\v\end{bmatrix}E(u,v)≈[uv]H[uv]，其中：
  H=∑(x,y)∈Wω(x,y)[Ix2IxIyIyIxIy2]H=\sum_{(x,y)\in W}\omega(x,y)\begin{bmatrix}I_x^2&I_xI_y\\I_yI_x&I_y^2\end{bmatrix}H=(x,y)∈W∑ω(x,y)[Ix2IyIxIxIyIy2]
  Ix,IyI_x,I_yIx,Iy为图像x/y方向梯度（Sobel算子计算）。

• 特征值分类逻辑 ：通过H的两个特征值λmax,λmin\lambda_{max},\lambda_{min}λmax,λmin判断像素类型：

  像素类型	特征值条件	灰度变化特性
  角点	λmax,λmin\lambda_{max},\lambda_{min}λmax,λmin均大且接近	任意方向平移均有显著变化
  边缘	一特征值大，一特征值小	沿边缘方向平移无变化
  平坦区域	两者均小	任意方向平移均无显著变化

2. 检测步骤（6步）

1. 高斯卷积平滑图像，计算x/y方向梯度Ix,IyI_x,I_yIx,Iy；
2. 对每个像素计算H矩阵；
3. 计算梯度乘积的加权和：Sx2=ω∗Ix2S_{x^2}=\omega*I_x^2Sx2=ω∗Ix2、Sy2=ω∗Iy2S_{y^2}=\omega*I_y^2Sy2=ω∗Iy2、Sxy=ω∗IxIyS_{xy}=\omega*I_xI_ySxy=ω∗IxIy；
4. 构建每个像素的H矩阵：H(x,y)=[Sx2SxySxySy2]H(x,y)=\begin{bmatrix}S_{x^2}&S_{xy}\\S_{xy}&S_{y^2}\end{bmatrix}H(x,y)=[Sx2SxySxySy2]；
5. 计算角点响应值：R=det(H)−αtrace(H)2R=det(H)-αtrace(H)^2R=det(H)−αtrace(H)2（det(H)=λ1λ2det(H)=\lambda_1\lambda_2det(H)=λ1λ2，trace(H)=λ1+λ2trace(H)=\lambda_1+\lambda_2trace(H)=λ1+λ2，α=0.06）；
6. 筛选角点：R>阈值且为局部极大值。

3. 特性与改进

• 核心特性 ：
  • 不变性：旋转不变 （H矩阵特征值旋转后不变）、光照不变（梯度对线性光照变化不敏感）；
  • 变异性：尺度不变性缺失（不同尺度下角点可能变为边缘/平坦区域）。
• 改进方案 ：
  • 问题：Harris检测的角点在高对比度区域分布密集，低对比度区域稀疏；
  • 解决：ANMS（自适应非极大值抑制）（Brown et al. 2005），筛选"局部极大值且响应值比半径r内邻居高10%"的点，实现均匀分布（如图40，ANMS后特征点空间分布更均匀）。

SIFT（尺度不变特征变换，核心点特征算法2）

1. 基础信息

• 提出：David Lowe（1999 ICCV，2004 IJCV精炼），引用超23000次；
• 核心优势 ：相比Harris，新增尺度不变性，且具有旋转/光照不变性，抗噪声、仿射变换、3D视角变化；
• 应用场景：图像检索、目标识别、视频跟踪、手势识别。

2. 完整流程（6步）

步骤	核心操作	关键参数/数字
1. 尺度空间构建	1. 高斯金字塔：每组S=5层，σ=1.52\sigma=1.52σ=1.52（修正相机初始模糊σ=0.5\sigma=0.5σ=0.5）； 2. DoG金字塔：相邻高斯层相减（近似LoG，效率更高）	组数O=[log2min(M,N)−3]O=[log_2min(M,N)-3]O=[log2min(M,N)−3]，DoG层数=S-1=4（S=5）
2. 局部极值检测	在3D尺度空间（x,y,σ）中，每个点与"同层8邻域+上下层9点"共26点比较，找极大/极小值	确保尺度连续性，k=2^(1/n)（n=2，每组内尺度间隔）
3. 关键点定位	1. 泰勒展开优化亚像素位置（剔除偏移>0.5的点）； 2. 剔除低对比度点（	D(̂x)
4. 方向分配	1. 以关键点为中心，1.5σ为半径，计算梯度幅值/方向； 2. 36°/柱构建梯度直方图，取峰值为主方向	高斯加权（1.5σ），直方图10柱（360°/36°）
5. 描述子生成	1. 取16×16区域，划分为4×4子块； 2. 每子块8方向直方图，生成128维向量	128维描述子（4×4×8），具有独特性
6. 特征匹配	1. k-d树搜索最近邻/次近邻； 2. 欧式距离度量相似性	匹配阈值：最近邻距离/次近邻距离<0.8（减少误匹配）

3. 核心特性验证

变换类型	特性表现
旋转	方向分配步骤确保旋转后描述子一致
尺度	高斯金字塔+DoG尺度空间，找到特征点的"特征尺度"，确保尺度不变
光照	梯度计算对线性光照变化（如I=aI+b）不敏感，描述子鲁棒
视角/仿射变换	局部区域描述子（16×16）对局部形变鲁棒

四、典型应用：全景拼接

1. 完整流程（5步）

1. 特征提取：提取每幅图像的SIFT特征点；
2. 特征匹配：k-d树寻找每个特征点的k个最近邻，筛选匹配对；
3. 图像配准 ：
   • 选择匹配点最多的m幅图像；
   • RANSAC算法计算两幅图像间的单应矩阵H（剔除 outliers）；
   • 贝叶斯后验概率验证匹配结果；
4. 连接集确定：寻找图像匹配的连接集，确定全景图数量；
5. 全景生成 ：
   • 捆绑调整（Bundle Adjustment）计算相机参数（焦距f、旋转矩阵R）；
   • 增益补偿（解决亮度差异）+多频段光度融合（消除拼接缝）。

---

关键问题

Harris角点检测与SIFT在"不变性、适用场景、计算复杂度"上的核心差异是什么？

两者核心差异如下表，源于设计目标的不同（Harris聚焦简单角点检测，SIFT聚焦尺度不变的通用特征）：

对比维度	Harris角点检测	SIFT（尺度不变特征变换）
不变性	旋转、光照不变；无尺度不变性	旋转、尺度、光照不变；抗仿射/视角变化
适用场景	低精度、实时性要求高的场景（如简单跟踪）	高精度、跨尺度/视角的场景（全景拼接、图像检索）
计算复杂度	低（仅需梯度计算+H矩阵，O(MN)）	高（高斯金字塔+128维描述子，O(MNlogMN)）
特征描述	无显式描述子（仅角点位置）	128维描述子（高独特性）
关键参数	α=0.06（响应函数）	128维描述子、σ=1.52（高斯初始值）

SIFT算法通过哪两个核心步骤实现"尺度不变性"？请结合"高斯金字塔"和"DoG尺度空间"的设计逻辑说明。

SIFT通过"构建多尺度空间 "和"特征尺度选择"两个核心步骤实现尺度不变性，具体逻辑如下：

1. 构建多尺度空间（高斯金字塔+DoG金字塔） ：
   • 高斯金字塔：将图像按组（Octave）和层（Level）缩放，每组图像尺寸减半，层间高斯模糊σ按2^(1/n)递增（n=2），覆盖不同尺度（如第0组σ=1.52，第1组σ=3.04）；
   • DoG金字塔：相邻高斯层相减得到DoG图像，近似LoG（拉普拉斯高斯），LoG空间具有"尺度归一化"特性（Lindeberg 1994），确保不同尺度下的特征点可比较。
2. 特征尺度选择 ：
   • 在3D DoG尺度空间（x,y,σ）中，通过"同层8邻域+上下层9点"的26点比较，找到局部极值点，该极值点对应的σ即为"特征尺度"；
   • 特征尺度确保：同一物理特征（如角点）在不同图像尺度下，均能被检测到且对应同一特征尺度，实现尺度不变性。

例如，文档中σ=2.5和σ=9.8的DoG图像，分别检测到小尺度和大尺度的特征点，且对应同一物理目标，验证了尺度不变性。

Harris角点检测中，H矩阵的特征值（λ_max,λ_min）如何区分"角点、边缘、平坦区域"？响应函数R=det(H)-αtrace(H)²的设计目的是什么？

1. H矩阵特征值的分类逻辑 ：

   H矩阵反映窗口内灰度梯度的分布，其特征值λ_max≥λ_min，对应灰度变化的"主方向"和"次方向"，分类规则如下：

   • 角点：λ_max和λ_min均较大且数值接近（如λ_max≈λ_min>阈值），说明窗口沿任意方向平移均有显著灰度变化，符合角点的定义；
   • 边缘：λ_max远大于λ_min（如λ_max>阈值，λ_min<阈值），说明窗口仅沿某一方向（边缘垂直方向）有灰度变化，沿边缘方向无变化，符合边缘的定义；
   • 平坦区域：λ_max和λ_min均较小（<阈值），说明窗口沿任意方向平移均无显著灰度变化，符合平坦区域的定义。

2. 响应函数R的设计目的 ：

   直接用λ_min判断角点（Shi-Tomasi 1994）虽简单，但对噪声敏感；Harris提出R=det(H)-αtrace(H)²（α=0.06），设计目的如下：

   • det(H)=λ_max * λ_min（反映特征值乘积，角点时大，边缘/平坦时小）；
   • trace(H)=λ_max+λ_min（反映特征值和，避免单一特征值大导致R误判）；
   • α为权重系数（0.04~0.06），平衡det(H)和trace(H)²，确保：
     • 角点：R>阈值（det(H)大，trace(H)²相对小）；
     • 边缘：R<0（λ_min小，det(H)≈0，trace(H)²大）；
     • 平坦区域：|R|小（det(H)和trace(H)²均小）；
       最终实现更鲁棒的角点筛选，减少噪声和边缘的误判。

---

14.光流与运动目标检测

核心内容包括：光流定义为图像中亮度模式的表观运动，需满足亮度一致性、空间连贯性、小运动 三大假设，因"孔径问题"（单像素仅1个方程无法解2个未知量u,v）需额外约束；光流计算分两类------Lucas-Kanade局部法 （利用空间连贯性，假设窗口内像素运动一致，通过最小二乘求解稀疏光流，适用于纹理丰富区域）和Horn-Schunck全局法 （引入全局平滑项，最小化能量函数得到稠密光流，对噪声敏感）；针对大运动场景，采用金字塔粗到精策略 （从低分辨率估算运动，逐步映射到高分辨率）；运动目标检测介绍三种方法------帧差法 （相邻帧差分阈值化，简单但易漏检）、背景减法 （当前帧减背景模型，背景建模用均值/中值，核心是背景更新）、光流法（通过光流向量差异提取运动目标，鲁棒但复杂）。

---

思维导图

---

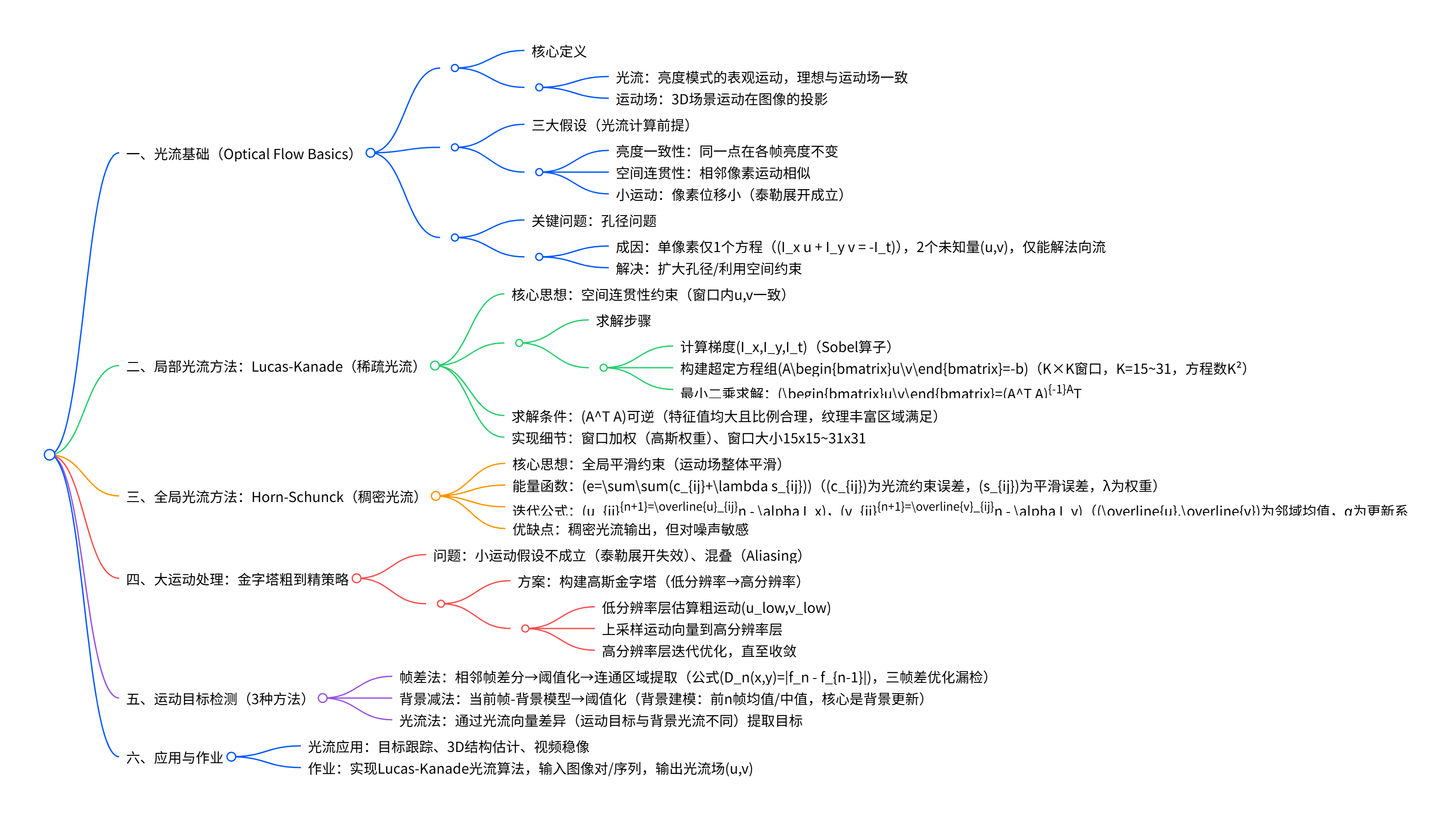
详细总结

光流基础（Optical Flow Basics）

1. 光流与运动场的定义

   • 光流 ：图像中亮度模式的表观运动，描述像素在连续帧间的位移向量(u,v)；理想情况下与"运动场"（3D场景运动在图像的投影）一致，但光照变化会导致光流与运动场偏离。
   • 运动场：3D场景中物体/相机运动在图像平面的投影，是真实运动的反映。

2. 光流计算的三大核心假设（文档11-16页）

   • 亮度一致性 ：同一空间点在不同帧的亮度不变，即I(x,y,t)=I(x+u,y+v,t+1)I(x,y,t)=I(x+u,y+v,t+1)I(x,y,t)=I(x+u,y+v,t+1)（核心方程推导基础）。
   • 空间连贯性：相邻像素属于同一表面，运动向量相似（解决"孔径问题"的关键约束）。
   • 小运动 ：像素位移小，满足泰勒展开的线性近似条件（I(x+u,y+v,t+1)≈I+Ixu+Iyv+ItI(x+u,y+v,t+1)\approx I + I_x u + I_y v + I_tI(x+u,y+v,t+1)≈I+Ixu+Iyv+It）。

3. 孔径问题（Aperture Problem）（文档18-21页）

   • 成因 ：单像素仅能构建1个光流约束方程Ixu+Iyv=−ItI_x u + I_y v = -I_tIxu+Iyv=−It，但存在2个未知量(u,v)，仅能求解"法向流"（垂直于边缘的运动分量），无法求解"切向流"（平行于边缘的运动分量）。
   • 解决策略：扩大孔径（利用更多像素的空间信息）或引入空间连贯性约束（如Lucas-Kanade的窗口假设）。

局部光流方法：Lucas-Kanade（稀疏光流）

1. 核心思想

   • 利用空间连贯性假设：假设K×K窗口（典型大小15x15~31x31）内所有像素的运动向量(u,v)相同，将单像素的欠定问题转化为超定问题（窗口内K²个方程，2个未知量）。

2. 数学求解过程

   • 步骤1：计算图像梯度IxI_xIx（x方向）、IyI_yIy（y方向）、ItI_tIt（时间方向）（常用Sobel算子或中心差分）。
   • 步骤2：构建超定方程组Ad=bA\mathbf{d} = \mathbf{b}Ad=b：
     A=[Ix(p1)Iy(p1)Ix(p2)Iy(p2)⋮⋮Ix(pK2)Iy(pK2)],d=[uv],b=−[It(p1)It(p2)⋮It(pK2)] A=\begin{bmatrix}I_x(p_1)&I_y(p_1)\\I_x(p_2)&I_y(p_2)\\\vdots&\vdots\\I_x(p_{K²})&I_y(p_{K²})\end{bmatrix},\quad \mathbf{d}=\begin{bmatrix}u\\v\end{bmatrix},\quad \mathbf{b}=-\begin{bmatrix}I_t(p_1)\\I_t(p_2)\\\vdots\\I_t(p_{K²})\end{bmatrix} A= Ix(p1)Ix(p2)⋮Ix(pK2)Iy(p1)Iy(p2)⋮Iy(pK2) ,d=[uv],b=− It(p1)It(p2)⋮It(pK2)
   • 步骤3：最小二乘求解：通过伪逆得到最优解d=(ATA)−1ATb\mathbf{d}=(A^T A)^{-1}A^T \mathbf{b}d=(ATA)−1ATb，展开为：

     ∑Ix2∑IxIy∑IxIy∑Iy2\]\[uv\]=−\[∑IxIt∑IyIt\] \\begin{bmatrix}\\sum I_x\^2\&\\sum I_x I_y\\\\\\sum I_x I_y\&\\sum I_y\^2\\end{bmatrix}\\begin{bmatrix}u\\\\v\\end{bmatrix}=-\\begin{bmatrix}\\sum I_x I_t\\\\\\sum I_y I_t\\end{bmatrix} \[∑Ix2∑IxIy∑IxIy∑Iy2\]\[uv\]=−\[∑IxIt∑IyIt

   • 步骤4：窗口加权：为降低边缘像素影响，常用高斯权重（窗口中心权重高，边缘低）。

3. 求解条件与适用场景

   • 求解条件：ATAA^T AATA需可逆且良态，即其两个特征值λ1,λ2\lambda_1,\lambda_2λ1,λ2均较大（避免低纹理区域），且λ1/λ2\lambda_1/\lambda_2λ1/λ2适中（避免边缘区域，类似Harris角点检测条件）。
   • 适用场景：纹理丰富区域的稀疏光流（仅跟踪特征点，如角点），实时性高，常用于目标跟踪。

全局光流方法：Horn-Schunck（稠密光流）

1. 核心思想

   • 引入全局平滑约束 ：假设光流场整体平滑（相邻像素运动向量差异小），通过最小化"光流约束误差+平滑误差"的全局能量函数，得到稠密光流（每个像素均有u,v）。

2. 能量函数与迭代求解

   • 能量函数：e=∑∑(cij+λsij)e=\sum\sum\left(c_{ij}+\lambda s_{ij}\right)e=∑∑(cij+λsij)，其中：
     • cij=(Ixuij+Iyvij+It)2c_{ij}=(I_x u_{ij}+I_y v_{ij}+I_t)^{2}cij=(Ixuij+Iyvij+It)2（光流约束误差，满足亮度一致性）；
     • sij=14[(ui+1,j−uij)2+(ui,j+1−uij)2+(vi+1,j−vij)2+(vi,j+1−vij)2]s_{ij}=\frac{1}{4}\left[(u_{i+1,j}-u_{ij})^2+(u_{i,j+1}-u_{ij})^2+(v_{i+1,j}-v_{ij})^2+(v_{i,j+1}-v_{ij})^2\right]sij=41[(ui+1,j−uij)2+(ui,j+1−uij)2+(vi+1,j−vij)2+(vi,j+1−vij)2]（平滑误差）；
     • λ\lambdaλ：平滑项权重（平衡约束与平滑，λ越大光流越平滑）。
   • 迭代公式：对能量函数求导并令导数为0，得到更新规则：
     uijn+1=u‾ijn−Ix(Ixu‾ijn+Iyv‾ijn+It)λ+Ix2+Iy2,vijn+1=v‾ijn−Iy(Ixu‾ijn+Iyv‾ijn+It)λ+Ix2+Iy2 u_{ij}^{n+1}=\overline{u}{ij}^n - \frac{I_x(I_x \overline{u}{ij}^n + I_y \overline{v}{ij}^n + I_t)}{\lambda + I_x^2 + I_y^2},\quad v{ij}^{n+1}=\overline{v}{ij}^n - \frac{I_y(I_x \overline{u}{ij}^n + I_y \overline{v}{ij}^n + I_t)}{\lambda + I_x^2 + I_y^2} uijn+1=uijn−λ+Ix2+Iy2Ix(Ixuijn+Iyvijn+It),vijn+1=vijn−λ+Ix2+Iy2Iy(Ixuijn+Iyvijn+It)
     （u‾ijn,v‾ijn\overline{u}{ij}^n,\overline{v}_{ij}^nuijn,vijn为第n次迭代时像素(i,j)的4邻域均值）。

3. 优缺点对比

   优点	缺点
   输出稠密光流（每个像素均有结果）	对噪声敏感（全局平滑放大噪声）
   无需手动选择特征点	迭代求解，实时性低于Lucas-Kanade
   适用于弱纹理区域	边缘区域光流精度较低

大运动处理：金字塔粗到精策略

1. 问题背景

   • 光流的"小运动假设"不成立时（像素位移大），泰勒展开误差大，直接求解会出现混叠（Aliasing）（近邻匹配错误）。

2. 解决策略：高斯金字塔（Coarse-to-Fine）

   • 步骤1：构建图像金字塔：对连续帧ItI_tIt和It+1I_{t+1}It+1分别构建高斯金字塔（从高分辨率→低分辨率，每层尺寸减半，高斯模糊）。
   • 步骤2：粗分辨率层求解：在最顶层（低分辨率）估算初始光流(ucoarse,vcoarse)(u_{coarse},v_{coarse})(ucoarse,vcoarse)（位移被缩小，满足小运动假设）。
   • 步骤3：上采样与精修：将粗层光流上采样（缩放至当前层尺寸），作为当前层的初始值，迭代优化；逐层向下，直至最高分辨率层，得到最终光流。

运动目标检测（Moving Object Detection）

方法名称	核心原理	关键公式/步骤	优缺点	适用场景
帧差法	相邻帧亮度差分→阈值化→连通区域提取	两帧差：$D_n(x,y)=	f_n - f_{n-1}	；<br>三帧差：；<br>三帧差：；<br>三帧差：D'n=D{n+1} \cap D_n$（优化漏检）
背景减法	当前帧 - 背景模型→阈值化→前景提取	背景模型： 1. 前n帧均值：B(x,y)=1n∑i=0n−1It−iB(x,y)=\frac{1}{n}\sum_{i=0}^{n-1}I_{t-i}B(x,y)=n1∑i=0n−1It−i； 2. 前n帧中值：B(x,y)=median{It−i}B(x,y)=median\{I_{t-i}\}B(x,y)=median{It−i}	优点：目标完整； 缺点：背景更新复杂（动态背景如树叶）	静态背景下的运动目标（如室内监控）
光流法	光流向量差异（运动目标与背景光流不同）提取目标	计算光流场→聚类光流向量→区分目标与背景光流	优点：鲁棒（不受光照/背景动态影响）； 缺点：计算复杂、实时性低	动态背景、复杂场景（如交通监控）

作业要求

• 任务：实现Lucas-Kanade光流算法；
• 输入：图像对或图像序列；
• 输出：光流场(u,v)(u,v)(u,v)（每个特征点的位移向量）；
• 参考资源：提供OpenCV/Python等代码链接（如http://opencv-python-tutroals.readthedocs.org）。

---

关键问题

Lucas-Kanade（局部光流）与Horn-Schunck（全局光流）在"约束条件、求解方式、光流类型、适用场景"上的核心差异是什么？请结合文档内容对比说明。

两者的核心差异源于"约束条件"的不同，具体对比如下：

对比维度	Lucas-Kanade（局部光流）	Horn-Schunck（全局光流）
约束条件	局部空间连贯性：假设K×K窗口（15x15~31x31）内像素运动一致，将欠定问题转化为超定问题	全局平滑约束：假设光流场整体平滑（相邻像素运动差异小），最小化全局能量函数
求解方式	最小二乘直接求解（d=(ATA)−1ATb\mathbf{d}=(A^T A)^{-1}A^T \mathbf{b}d=(ATA)−1ATb），非迭代	迭代求解（能量函数求导→更新规则，需多轮迭代收敛）
光流类型	稀疏光流：仅求解特征点（如角点）的光流，非特征点无结果	稠密光流：每个像素均有光流结果，覆盖全图像
适用场景	实时性要求高、纹理丰富的场景（如目标跟踪、视频稳像）	需稠密光流、弱纹理区域的场景（如3D结构估计）
对噪声敏感性	抗噪声（窗口加权平滑局部噪声）	对噪声敏感（全局平滑放大噪声）

光流计算的"三大假设"分别有什么作用？"孔径问题"的本质是什么？如何通过算法设计解决孔径问题？

1. 三大假设的作用：

   • 亮度一致性假设 ：是光流约束方程的推导基础，将"像素运动"与"亮度变化"关联，得到核心方程Ixu+Iyv=−ItI_x u + I_y v = -I_tIxu+Iyv=−It（文档16页）；
   • 空间连贯性假设：解决"孔径问题"的核心，通过假设相邻像素运动相似，为单像素的欠定方程补充约束（Lucas-Kanade的窗口约束、Horn-Schunck的全局平滑均基于此）；
   • 小运动假设 ：确保泰勒展开的线性近似成立（I(x+u,y+v,t+1)≈I+Ixu+Iyv+ItI(x+u,y+v,t+1)\approx I + I_x u + I_y v + I_tI(x+u,y+v,t+1)≈I+Ixu+Iyv+It），是光流线性求解的前提。

2. 孔径问题的本质 ：

   单像素仅能提供1个光流约束方程（Ixu+Iyv=−ItI_x u + I_y v = -I_tIxu+Iyv=−It），但存在2个未知量（u：x方向位移，v：y方向位移），属于欠定问题，仅能求解"法向流"（垂直于边缘的运动分量），无法求解"切向流"（平行于边缘的运动分量）（文档18-21页）。

3. 解决策略：

   • 扩大孔径：增加窗口内像素数量，利用空间连贯性假设（如Lucas-Kanade用15x15窗口，得到225个方程，超定求解）；
   • 全局约束：引入全局平滑项（如Horn-Schunck的能量函数），从全局角度约束光流场，补充局部约束不足。

运动目标检测的"帧差法""背景减法""光流法"各有什么核心局限？在实际应用中如何选择？

1. 各方法的核心局限：

   • 帧差法：①"小运动失效"（像素位移小于1像素时，差分结果低于阈值，漏检）；②"边缘不完整"（差分仅保留目标边缘，内部空洞）；③"对光照敏感"（光照突变误判为运动目标）；
   • 背景减法：①"动态背景难建模"（如树叶晃动、水面波纹，背景模型易污染）；②"背景更新滞后"（缓慢变化的背景如阴影，无法及时更新，导致目标残留）；
   • 光流法：①"计算复杂"（尤其是稠密光流，实时性低）；②"弱纹理区域精度低"（光流求解依赖梯度，弱纹理区域梯度小，光流误差大）。

2. 实际应用选择原则：

   • 若场景为静态背景、快速运动目标、实时性要求高 （如室内监控、工业流水线）：选帧差法（优先三帧差优化漏检）；
   • 若场景为静态背景、慢运动目标、需完整目标轮廓 （如商场人流统计）：选背景减法（背景建模用中值法抗噪声，加背景更新策略）；
   • 若场景为动态背景、复杂光照、需鲁棒检测 （如交通监控、户外场景）：选光流法（结合金字塔解决大运动，用稀疏光流平衡实时性与精度）。

---

15.双目立体视觉与3D重建

核心是通过双相机拍摄的图像恢复场景3D几何，首先介绍图像中3D信息的提取线索（如阴影、纹理、运动等），随后阐述双目立体的核心原理------基于三角测量（Triangulation） ，通过计算对应点的视差（Disparity） 推导深度（公式z=fbdz=\frac{fb}{d}z=dfb，fff为焦距、bbb为基线、ddd为视差）；关键步骤包括利用极线约束（Epipolar Constraint） 将对应点匹配从2D搜索降为1D，通过图像校正（Rectification） 使极线平行以简化匹配，采用窗口匹配（如SSD、相关性）解决对应点问题；还详细讲解双目标定（相对定向 需5对对应点、绝对定向 需3个非共线点）、基础矩阵（Fundamental Matrix） 的8点估计算法（秩2约束），最后补充结构光扫描（单条纹、二进制编码等）作为双目立体的补充，实现高精度3D扫描与建模。

---

思维导图

---

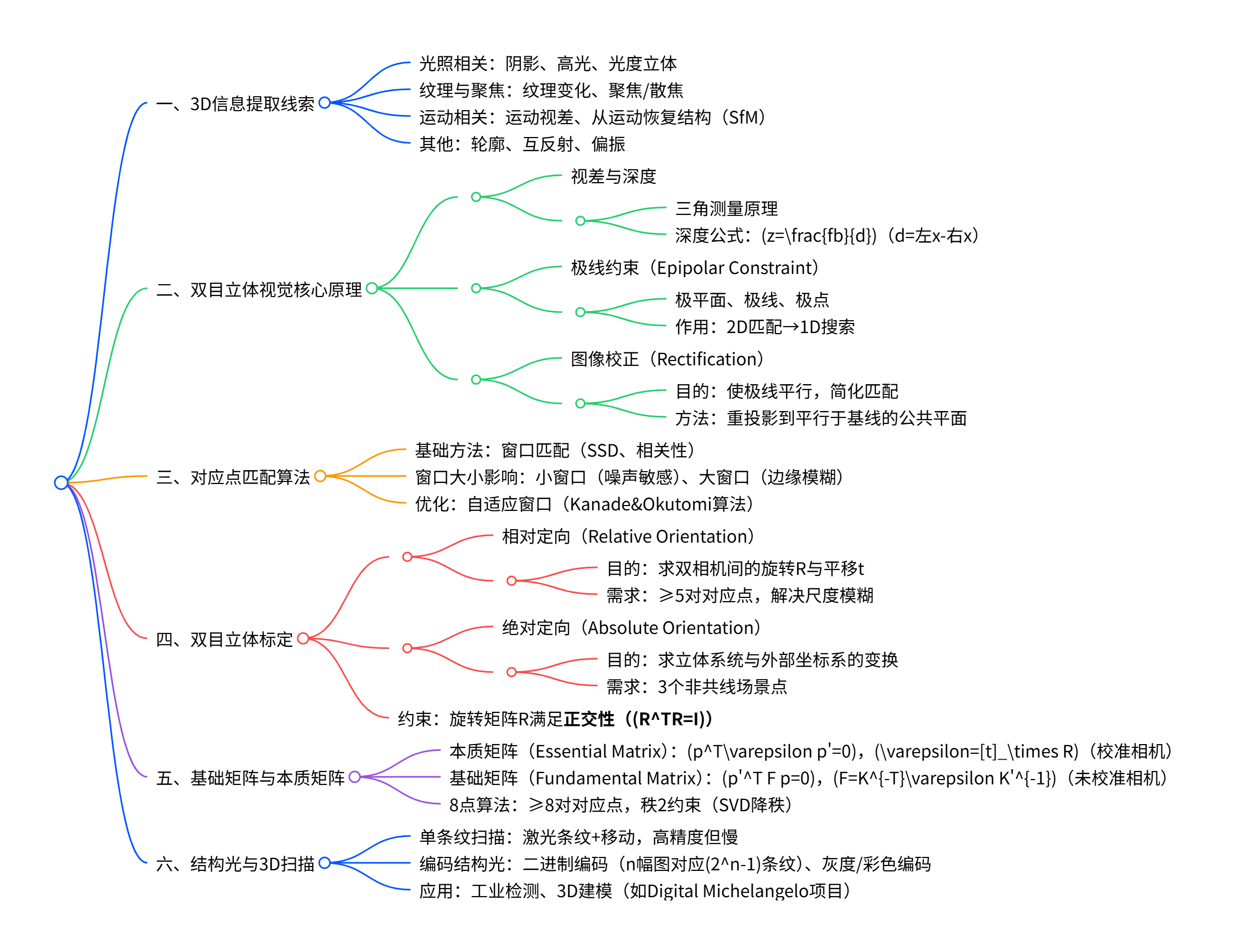
详细总结

图像中的3D信息提取线索

文档首先列举了从2D图像恢复3D信息的关键线索，这些是立体视觉的基础支撑：

线索类型	具体形式	作用
光照相关	阴影（Shading）、高光（Highlights）、光度立体（Photometric Stereo）	从亮度变化推断表面法向与深度
纹理与聚焦	纹理密度变化、聚焦/散焦（Focus/Defocus）	纹理稀疏→远，聚焦区域→深度匹配
运动相关	运动视差、从运动恢复结构（SfM）	多帧运动图像关联3D结构
其他线索	轮廓（Silhouettes）、互反射（Inter-reflections）、偏振（Polarization）	辅助约束3D形状边界

双目立体视觉基础原理

1. 视差（Disparity）与深度（Depth）的关系

• 核心依据 ：三角测量原理 ，假设双相机光轴平行，焦距为fff，基线（两相机光心距离）为bbb。
• 关键公式推导 ：
  对3D点P(x,y,z)P(x,y,z)P(x,y,z)，左相机投影点(xl,yl)(x_l,y_l)(xl,yl)、右相机投影点(xr,yr)(x_r,y_r)(xr,yr)，由相似三角形得：
  zf=xxl=x−bxr\frac{z}{f}=\frac{x}{x_l}=\frac{x-b}{x_r}fz=xlx=xrx−b，整理得视差d=xl−xrd=x_l-x_rd=xl−xr，深度公式：
  z=fbd\boldsymbol{z=\frac{fb}{d}}z=dfb
  结论：深度与视差成反比，视差越大，物体越近。
• 关键问题 ：需解决两个核心问题------①找到左/右图像的对应点(xl,yl)(x_l,y_l)(xl,yl)与(xr,yr)(x_r,y_r)(xr,yr)（对应点匹配问题）；②已知相机内参（fff）与外参（bbb）（相机标定问题）。

2. 极线约束（Epipolar Constraint）

• 定义 ：过左相机光心ClC_lCl、右相机光心CrC_rCr与3D点PPP的平面为极平面 ，极平面与左/右图像平面的交线为极线 ，两光心连线与图像平面的交点为极点。
• 作用：将对应点匹配从"2D全图搜索"简化为"1D极线搜索"，大幅降低计算复杂度，是双目匹配的核心约束。

3. 图像校正（Stereo Image Rectification）

• 目的 ：通过单应变换将左/右图像重投影到平行于基线的公共平面，使对应极线变为水平且对齐，此时对应点仅在同一行搜索，进一步简化匹配。
• 关键步骤 ：
  1. 计算新旋转矩阵RRR：以基线方向为r1r_1r1（r1=(c1−c2)/∥c1−c2∥r_1=(c_1-c_2)/\Vert c_1-c_2\Vertr1=(c1−c2)/∥c1−c2∥），构建正交坐标系r2=r1×[0,0,1]Tr_2=r_1×[0,0,1]^Tr2=r1×[0,0,1]T、r3=r1×r2r_3=r_1×r_2r3=r1×r2；
  2. 重投影左/右图像，更新相机投影矩阵P~1=A[R∣t~1]\tilde{P}_1=A[R|\tilde{t}_1]P~1=A[R∣t~1]、P~2=A[R∣t~2]\tilde{P}_2=A[R|\tilde{t}_2]P~2=A[R∣t~2]；
  3. 优化重采样误差，确保校正后无明显畸变（Good Rectification需避免边缘拉伸）。

对应点匹配算法

1. 基础匹配逻辑

• 核心思想：对左图像每个像素，在右图像对应极线上（校正后为同一行），通过"窗口匹配"计算相似度，选择最优像素作为对应点。
• 相似度度量：Sum of Squared Difference（SSD）、归一化互相关（NCC）等。

2. 窗口大小的影响

窗口大小	优点	缺点	适用场景
小窗口（如8×8）	对边缘细节保留好，适用于纹理丰富区域	对噪声敏感，易匹配错误	精细结构场景（如小物体）
大窗口（如20×20）	抗噪声能力强，匹配更稳定	模糊边缘，易跨物体匹配	低纹理场景（如墙面）
自适应窗口	平衡细节与抗噪声，动态调整窗口大小	计算复杂度高	复杂纹理场景（Kanade&Okutomi算法）

双目立体标定

标定是获取相机内参（焦距fff、主点(u0,v0)(u_0,v_0)(u0,v0)）与外参（旋转RRR、平移ttt）的关键步骤，分两类：

标定类型	目的	输入需求	关键约束
相对定向	求左相机相对于右相机的RRR与ttt	≥5对图像对应点（无场景3D坐标）	旋转矩阵正交性（RTR=IR^TR=IRTR=I），尺度模糊（需固定ttt的模）
绝对定向	求立体系统相对于外部坐标系的RRR与ttt	3个非共线场景点的左/右系统3D坐标	无尺度模糊，需场景点真实3D坐标
求解方法	最小化重投影误差	超定系统（多组对应点）	带正交约束的非线性优化（E=∑∥ei∥2+λ(RTR−I)E=\sum\Vert e_i\Vert^2+\lambda(R^TR-I)E=∑∥ei∥2+λ(RTR−I)）

基础矩阵（Fundamental Matrix）

1. 定义与作用

• 核心公式 ：对未校准相机，对应点x=(u,v,1)Tx=(u,v,1)^Tx=(u,v,1)T与x′=(u′,v′,1)Tx'=(u',v',1)^Tx′=(u′,v′,1)T满足x′TFx=0\boldsymbol{x'^T F x=0}x′TFx=0，其中F=K−TεK′−1F=K^{-T}\varepsilon K'^{-1}F=K−TεK′−1（ε=[t]×R\varepsilon=[t]_\times Rε=[t]×R为本质矩阵，KKK为相机内参）。
• 性质：3×3矩阵，秩为2，7个自由度（9个元素-1个尺度-1个秩约束）。

2. 8点算法（Estimation）

• 步骤 ：
  1. 构建线性方程组：每对对应点生成1个方程uu′f11+vu′f12+u′f13+uv′f21+vv′f22+v′f23+uf31+vf32+f33=0uu'f_{11}+vu'f_{12}+u'f_{13}+uv'f_{21}+vv'f_{22}+v'f_{23}+uf_{31}+vf_{32}+f_{33}=0uu′f11+vu′f12+u′f13+uv′f21+vv′f22+v′f23+uf31+vf32+f33=0，8对对应点生成8×9矩阵UUU；
  2. 求解最小二乘：求UTUU^TUUTU的最小特征值对应的特征向量，即为FFF的初始解；
  3. 秩约束修正：因噪声导致初始FFF可能秩为3，通过SVD分解F=UΣVTF=U\Sigma V^TF=UΣVT，令Σ′=diag(σ1,σ2,0)\Sigma'=\text{diag}(\sigma_1,\sigma_2,0)Σ′=diag(σ1,σ2,0)，得到秩2的F′=UΣ′VTF'=U\Sigma' V^TF′=UΣ′VT。

结构光与3D扫描

作为双目立体的补充，通过投影结构化光解决对应点匹配难题，实现高精度3D扫描：

结构光类型	原理	优点	缺点
单条纹扫描	投影激光条纹，沿物体移动扫描	精度高（<0.01mm）	慢，需多帧图像（Cyberware扫描仪）
二进制编码光	投影nnn幅二进制图案，每像素生成nnn位编码	快（2n−12^n-12n−1条纹仅需nnn幅图）	对遮挡敏感
实时3D重建	投影复杂图案（如随机散斑），单帧匹配	实时性强（30Hz）	精度略低，需复杂匹配算法
应用案例	Digital Michelangelo项目、Microsoft Kinect	覆盖工业检测、数字文物建模等	------

---

关键问题

双目立体视觉中，深度与视差的关系是如何推导的？该关系反映了二者怎样的内在联系？

答案 ：

推导依据是平行光轴双相机的相似三角形原理，具体步骤如下：

1. 假设双相机光轴平行，左相机光心ClC_lCl、右相机光心CrC_rCr，基线长度b=∥ClCr∥b=\Vert C_lC_r\Vertb=∥ClCr∥，焦距均为fff；
2. 3D点P(x,y,z)P(x,y,z)P(x,y,z)在左图像投影为(xl,yl)(x_l,y_l)(xl,yl)，右图像投影为(xr,yr)(x_r,y_r)(xr,yr)，因光轴平行，yl=yry_l=y_ryl=yr；
3. 对左相机，由相似三角形zf=xxl\frac{z}{f}=\frac{x}{x_l}fz=xlx；对右相机，zf=x−bxr\frac{z}{f}=\frac{x-b}{x_r}fz=xrx−b；
4. 联立两式消去xxx，得视差d=xl−xrd=x_l-x_rd=xl−xr，整理得深度公式z=fbd\boldsymbol{z=\frac{fb}{d}}z=dfb。

内在联系：深度与视差成反比------视差越大（左/右投影点横向距离越远），物体越近；视差越小，物体越远，这是双目立体通过2D视差恢复3D深度的核心依据。

极线约束在双目对应点匹配中起到什么作用？图像校正为何能进一步简化匹配过程？

答案：

1. 极线约束的作用 ：

   极线约束源于"3D点PPP、左光心ClC_lCl、右光心CrC_rCr共面（极平面）"，导致右图像中PPP的对应点必在极线上，左图像对应点同理。该约束将对应点匹配从"2D全图搜索"（复杂度O(MN)O(MN)O(MN)）降为"1D极线搜索"（复杂度O(M)O(M)O(M)或O(N)O(N)O(N)），大幅降低计算量，避免无效搜索。

2. 图像校正的目的与简化原理 ：

   图像校正通过单应变换，将左/右图像重投影到平行于基线的公共平面 ，使校正后的极线满足两个条件：①极线水平；②左/右图像的对应极线位于同一行。

   此时，左图像中任意像素(u,v)(u,v)(u,v)的对应点必在右图像的第vvv行，匹配仅需在同一行滑动窗口搜索，无需再沿倾斜极线查找，进一步将匹配复杂度从"1D任意方向"简化为"1D水平方向"，且便于硬件加速。

基础矩阵的8点算法为何需要对初始解进行"秩2约束"修正？该约束的物理意义是什么？

答案：

1. 秩2约束修正的原因 ：

   基础矩阵FFF的理论秩为2，源于其定义F=K−TεK′−1F=K^{-T}\varepsilon K'^{-1}F=K−TεK′−1------本质矩阵ε=[t]×R\varepsilon=[t]_\times Rε=[t]×R是3×3反对称矩阵与旋转矩阵的乘积，秩为2，因此FFF的秩也为2。但在实际计算中，由于图像噪声、对应点匹配误差，通过8点算法得到的初始FFF可能秩为3，违背理论约束，若直接使用会导致极线不相交于极点，产生匹配错误，因此需通过SVD分解将最小奇异值置0，强制FFF秩为2。

2. 秩2约束的物理意义：

• 秩2约束对应双目立体的极线几何一致性 ------所有极线必须相交于极点（左极点在右图像的极线上，右极点在左图像的极线上）。若FFF秩为3，极线会呈现无规律分布，无法满足"3D点、双光心共面"的物理规律，导致后续3D重建结果失真；秩2约束确保FFF符合双目成像的几何本质，保证极线约束的有效性。

• 求解最小二乘：求UTUU^TUUTU的最小特征值对应的特征向量，即为FFF的初始解；

• 秩约束修正：因噪声导致初始FFF可能秩为3，通过SVD分解F=UΣVTF=U\Sigma V^TF=UΣVT，令Σ′=diag(σ1,σ2,0)\Sigma'=\text{diag}(\sigma_1,\sigma_2,0)Σ′=diag(σ1,σ2,0)，得到秩2的F′=UΣ′VTF'=U\Sigma' V^TF′=UΣ′VT。

结构光与3D扫描

作为双目立体的补充，通过投影结构化光解决对应点匹配难题，实现高精度3D扫描：

结构光类型	原理	优点	缺点
单条纹扫描	投影激光条纹，沿物体移动扫描	精度高（<0.01mm）	慢，需多帧图像（Cyberware扫描仪）
二进制编码光	投影nnn幅二进制图案，每像素生成nnn位编码	快（2n−12^n-12n−1条纹仅需nnn幅图）	对遮挡敏感
实时3D重建	投影复杂图案（如随机散斑），单帧匹配	实时性强（30Hz）	精度略低，需复杂匹配算法
应用案例	Digital Michelangelo项目、Microsoft Kinect	覆盖工业检测、数字文物建模等	------

---

关键问题

双目立体视觉中，深度与视差的关系是如何推导的？该关系反映了二者怎样的内在联系？

推导依据是平行光轴双相机的相似三角形原理，具体步骤如下：

1. 假设双相机光轴平行，左相机光心ClC_lCl、右相机光心CrC_rCr，基线长度b=∥ClCr∥b=\Vert C_lC_r\Vertb=∥ClCr∥，焦距均为fff；
2. 3D点P(x,y,z)P(x,y,z)P(x,y,z)在左图像投影为(xl,yl)(x_l,y_l)(xl,yl)，右图像投影为(xr,yr)(x_r,y_r)(xr,yr)，因光轴平行，yl=yry_l=y_ryl=yr；
3. 对左相机，由相似三角形zf=xxl\frac{z}{f}=\frac{x}{x_l}fz=xlx；对右相机，zf=x−bxr\frac{z}{f}=\frac{x-b}{x_r}fz=xrx−b；
4. 联立两式消去xxx，得视差d=xl−xrd=x_l-x_rd=xl−xr，整理得深度公式z=fbd\boldsymbol{z=\frac{fb}{d}}z=dfb。

内在联系：深度与视差成反比------视差越大（左/右投影点横向距离越远），物体越近；视差越小，物体越远，这是双目立体通过2D视差恢复3D深度的核心依据。

极线约束在双目对应点匹配中起到什么作用？图像校正为何能进一步简化匹配过程？

1. 极线约束的作用 ：

   极线约束源于"3D点PPP、左光心ClC_lCl、右光心CrC_rCr共面（极平面）"，导致右图像中PPP的对应点必在极线上，左图像对应点同理。该约束将对应点匹配从"2D全图搜索"（复杂度O(MN)O(MN)O(MN)）降为"1D极线搜索"（复杂度O(M)O(M)O(M)或O(N)O(N)O(N)），大幅降低计算量，避免无效搜索。

2. 图像校正的目的与简化原理 ：

   图像校正通过单应变换，将左/右图像重投影到平行于基线的公共平面 ，使校正后的极线满足两个条件：①极线水平；②左/右图像的对应极线位于同一行。

   此时，左图像中任意像素(u,v)(u,v)(u,v)的对应点必在右图像的第vvv行，匹配仅需在同一行滑动窗口搜索，无需再沿倾斜极线查找，进一步将匹配复杂度从"1D任意方向"简化为"1D水平方向"，且便于硬件加速。

基础矩阵的8点算法为何需要对初始解进行"秩2约束"修正？该约束的物理意义是什么？

1. 秩2约束修正的原因 ：

   基础矩阵FFF的理论秩为2，源于其定义F=K−TεK′−1F=K^{-T}\varepsilon K'^{-1}F=K−TεK′−1------本质矩阵ε=[t]×R\varepsilon=[t]_\times Rε=[t]×R是3×3反对称矩阵与旋转矩阵的乘积，秩为2，因此FFF的秩也为2。但在实际计算中，由于图像噪声、对应点匹配误差，通过8点算法得到的初始FFF可能秩为3，违背理论约束，若直接使用会导致极线不相交于极点，产生匹配错误，因此需通过SVD分解将最小奇异值置0，强制FFF秩为2。

2. 秩2约束的物理意义 ：

   秩2约束对应双目立体的极线几何一致性 ------所有极线必须相交于极点（左极点在右图像的极线上，右极点在左图像的极线上）。若FFF秩为3，极线会呈现无规律分布，无法满足"3D点、双光心共面"的物理规律，导致后续3D重建结果失真；秩2约束确保FFF符合双目成像的几何本质，保证极线约束的有效性。