LeetCode 84. 柱状图中最大的矩形（困难）

题目描述

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例

示例 1：

复制代码

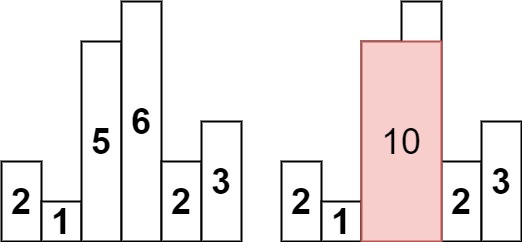
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

复制代码

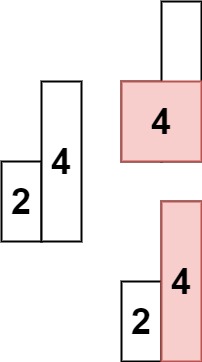
输入： heights = [2,4]
输出： 4

解法

1.暴力（跑不通所有样例）

解题思路

如果我们想暴力解决这个问题，需要遍历heights数组每个元素，分别从i位置向左和向右查找比heights[i]小元素的坐标，这样以heights[i]为高矩形的宽就是right-left-1,然后计算出不同高矩形的面积，取最大值。这种做法的时间复杂度是O(n^2)，大概率跑不通所有样例。

cpp 复制代码

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int n = heights.size();
        int s_max = 0;
        for(int i = 0;i < n;i ++){
             int left = i,right = i;
             while(left >= 0 && heights[left] >= heights[i]) left --;
             while(right < n && heights[right] >= heights[i]) right ++;
             int s = (right - left  - 1) * heights[i];
             s_max = max(s,s_max);
        }
        return s_max;
    }
};

时间复杂度O（N^2），空间复杂度O（1）

2.单调栈

解题思路：

与暴力解法中为每个柱子向左右双向扩展寻找边界相比，单调栈解法的核心思想是利用栈的单调递增性质，在单向遍历过程中动态记录边界信息：当遇到较矮柱子时，栈中较高柱子的右边界被确定并弹出，而当前柱子的左边界就是弹出后栈顶的柱子，这样通过维护一个高度递增的栈结构，在O(n)时间内就完成了所有柱子左右边界的计算。

cpp 复制代码

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int n = heights.size();
        vector<int> left(n,-1); // 左边界数组，初始为-1（左边界在数组外）
        vector<int> right(n,n); // 右边界数组，初始为n（右边界在数组外）
        stack<pair<int,int>> st; // 单调栈，存储{高度, 索引}
        int s = 0,s_max = 0;
        for(int i = 0;i < n;i ++){
            while(!st.empty() && heights[i] < st.top().first){
                right[st.top().second] = i; // 当前柱子是栈顶柱子的右边界
                st.pop();
            }
            if(!st.empty()){
                left[i] = st.top().second; // 栈顶柱子是当前柱子的左边界
            }
            st.push({heights[i],i}); //将当前柱子压入栈中，保持栈的单调递增性
        }
        //计算最大面积
        for(int i = 0;i < n;i ++){
            s = (right[i] - left[i] - 1) * heights[i];
            s_max = max(s_max,s);
        }
        return s_max;
    }
};

时间复杂度O（N），空间复杂度O（N）

LeetCode 84. 柱状图中最大的矩形（困难）

题目描述

示例

解法

1.暴力（跑不通所有样例）

**2.**单调栈

2.单调栈