已知 空间 三个 A，B C 点 ，求 顺序 经过 A B C 三点 圆弧 轨迹 ，给出 python 代码 并且 画出图像

以下是计算空间中经过三点 A、B、C 的圆弧轨迹并进行 3D 可视化的 Python 代码。代码会先计算圆弧参数，然后使用 matplotlib 绘制出三点、圆弧轨迹、圆心以及相关辅助线：

import numpy as np
from numpy.linalg import solve, norm
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 设置中文显示
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
plt.rcParams["axes.unicode_minus"] = False  # 正确显示负号

def find_circular_arc(A, B, C, num_points=100):
    """
    计算空间中经过三点A、B、C的圆弧轨迹
    
    参数:
        A, B, C: 三维空间中的点，格式为numpy数组或列表
        num_points: 生成的圆弧上的点的数量（包括A和C）
    
    返回:
        arc_points: 圆弧上的点组成的数组，形状为(num_points, 3)
        center: 圆弧所在圆的圆心
        radius: 圆弧的半径
    """
    # 转换为numpy数组
    A = np.array(A, dtype=np.float64)
    B = np.array(B, dtype=np.float64)
    C = np.array(C, dtype=np.float64)
    
    # 检查三点是否共线
    AB = B - A
    AC = C - A
    cross = np.cross(AB, AC)
    
    if norm(cross) < 1e-10:
        raise ValueError("三点共线，无法确定圆弧")
    
    # 计算平面法向量（AB × AC）
    n = cross / norm(cross)  # 单位法向量
    
    # 求解外接圆圆心：解线性方程组得到s和t
    AB_dot_AB = np.dot(AB, AB)
    AB_dot_AC = np.dot(AB, AC)
    AC_dot_AC = np.dot(AC, AC)
    
    # 右边的常数项
    rhs = np.array([0.5 * AB_dot_AB, 0.5 * AC_dot_AC])
    
    # 系数矩阵
    mat = np.array([[AB_dot_AB, AB_dot_AC], [AB_dot_AC, AC_dot_AC]])
    
    # 求解s和t
    s, t = solve(mat, rhs)
    
    # 计算圆心
    center = A + s * AB + t * AC
    
    # 计算半径
    radius = norm(A - center)
    
    # 计算三点相对于圆心的向量
    OA = A - center
    OB = B - center
    OC = C - center
    
    # 计算平面内的两个正交单位向量（用于角度计算）
    u = OA / radius
    v = np.cross(n, u)  # 垂直于u且在平面内的单位向量
    
    # 计算三点对应的角度
    theta_A = 0.0  # A点作为角度起点
    theta_B = np.arctan2(np.dot(OB, v), np.dot(OB, u))
    theta_C = np.arctan2(np.dot(OC, v), np.dot(OC, u))
    
    # 确保角度顺序正确（经过B点）
    delta1 = theta_B - theta_A
    delta2 = theta_C - theta_B
    
    # 处理角度跨0点的情况
    if delta1 < -np.pi:
        delta1 += 2 * np.pi
    elif delta1 > np.pi:
        delta1 -= 2 * np.pi
        
    if delta2 < -np.pi:
        delta2 += 2 * np.pi
    elif delta2 > np.pi:
        delta2 -= 2 * np.pi
    
    # 确定总角度范围
    total_delta = delta1 + delta2
    thetas = np.linspace(theta_A, theta_A + total_delta, num_points)
    
    # 生成圆弧上的点
    arc_points = [center + radius * (np.cos(theta) * u + np.sin(theta) * v) for theta in thetas]
    
    return np.array(arc_points), center, radius

def plot_arc(A, B, C, arc_points, center):
    """绘制三点、圆弧和相关信息"""
    fig = plt.figure(figsize=(10, 8))
    ax = fig.add_subplot(111, projection='3d')
    
    # 绘制圆弧
    ax.plot(arc_points[:, 0], arc_points[:, 1], arc_points[:, 2], 'b-', label='圆弧轨迹')
    
    # 绘制三点
    ax.scatter(A[0], A[1], A[2], c='r', s=100, label='点A')
    ax.scatter(B[0], B[1], B[2], c='g', s=100, label='点B')
    ax.scatter(C[0], C[1], C[2], c='y', s=100, label='点C')
    
    # 绘制圆心
    ax.scatter(center[0], center[1], center[2], c='m', s=100, marker='*', label='圆心O')
    
    # 绘制从圆心到三点的连线
    ax.plot([center[0], A[0]], [center[1], A[1]], [center[2], A[2]], 'k--', alpha=0.5)
    ax.plot([center[0], B[0]], [center[1], B[1]], [center[2], B[2]], 'k--', alpha=0.5)
    ax.plot([center[0], C[0]], [center[1], C[1]], [center[2], C[2]], 'k--', alpha=0.5)
    
    # 设置坐标轴标签
    ax.set_xlabel('X轴')
    ax.set_ylabel('Y轴')
    ax.set_zlabel('Z轴')
    
    # 添加标题和图例
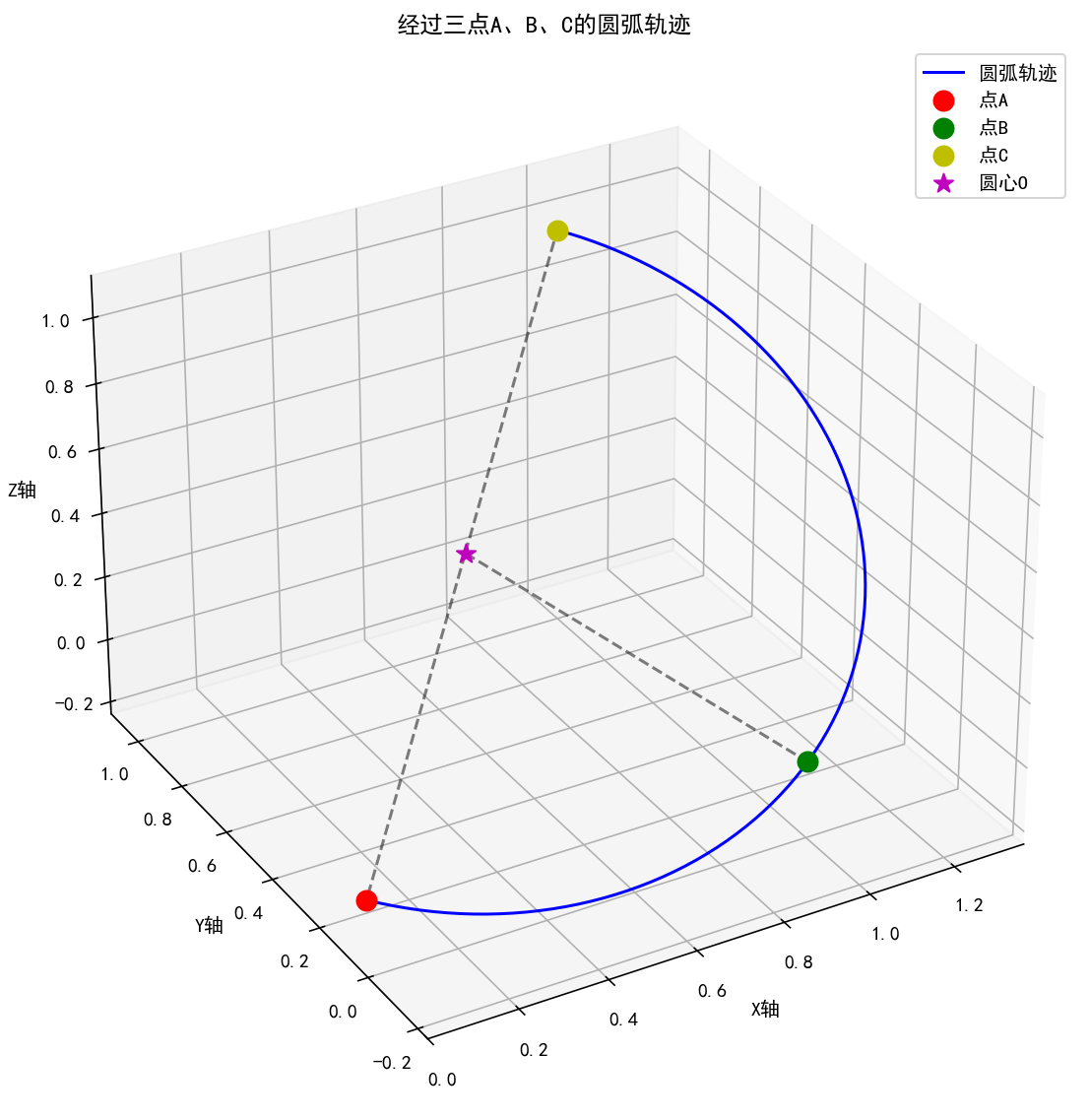
    ax.set_title('经过三点A、B、C的圆弧轨迹')
    ax.legend()
    
    # 调整视角
    ax.view_init(elev=30, azim=-120)
    
    # 使坐标轴比例一致
    all_points = np.vstack([arc_points, A, B, C, center])
    max_range = np.array([
        all_points[:, 0].max() - all_points[:, 0].min(),
        all_points[:, 1].max() - all_points[:, 1].min(),
        all_points[:, 2].max() - all_points[:, 2].min()
    ]).max() / 2
    
    mid_x = (all_points[:, 0].max() + all_points[:, 0].min()) / 2
    mid_y = (all_points[:, 1].max() + all_points[:, 1].min()) / 2
    mid_z = (all_points[:, 2].max() + all_points[:, 2].min()) / 2
    
    ax.set_xlim(mid_x - max_range, mid_x + max_range)
    ax.set_ylim(mid_y - max_range, mid_y + max_range)
    ax.set_zlim(mid_z - max_range, mid_z + max_range)
    
    plt.tight_layout()
    plt.show()

# 示例用法
if __name__ == "__main__":
    # 定义三个空间点（可修改为任意不共线的三维点）
    A = [0, 0, 0]
    B = [1, 0, 0]
    C = [1, 1, 1]  # 非平面示例，展示3D效果
    
    try:
        arc_points, center, radius = find_circular_arc(A, B, C, num_points=100)
        
        print(f"圆心坐标: {center}")
        print(f"圆弧半径: {radius:.6f}")
        print(f"生成的圆弧点数量: {len(arc_points)}")
        
        # 绘制图像
        plot_arc(A, B, C, arc_points, center)
    
    except ValueError as e:
        print(e)