数据结构 -- 栈

遗憾是什么.2025-11-13 13:41

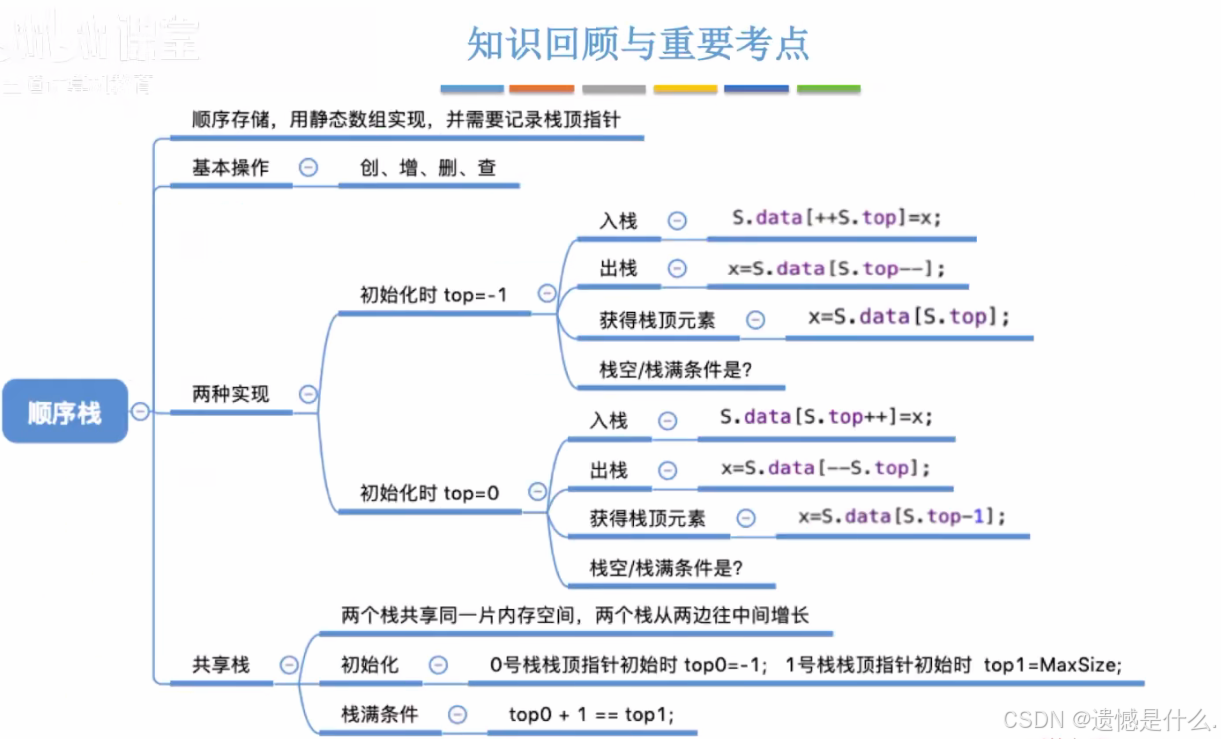
一.栈的定义

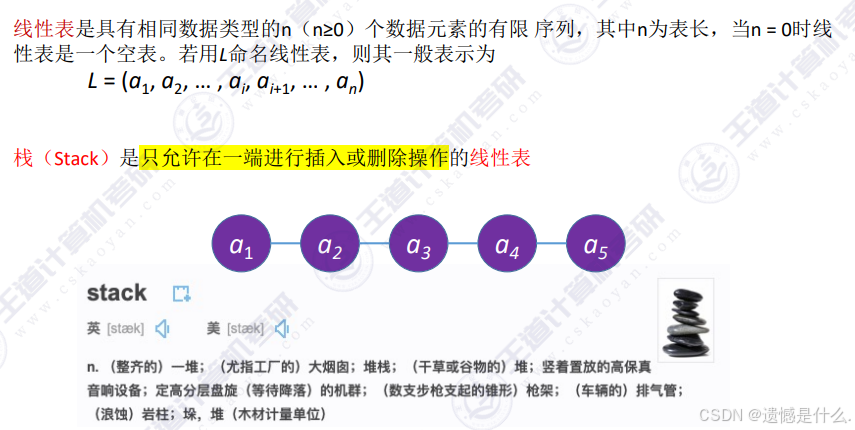
栈(Stack)是只允许在一段进行插入或删除操作的线性表;

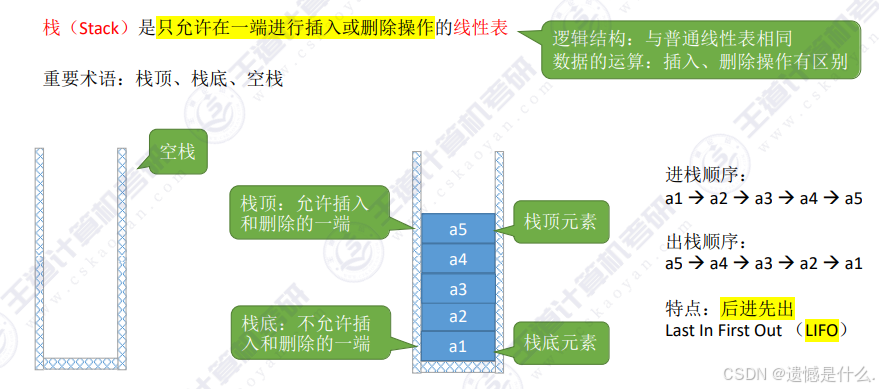
栈和线性表的基本操作:

出栈顺序:

二.栈的初始化

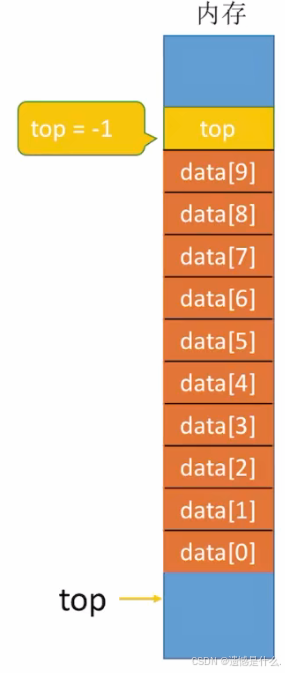当栈空时, data[0] - data[9]全空, 则top指向data[0]上一个元素, 即top = -1.

所以判断栈是否为空, 只需观察top指向哪里,

当top = -1时, 栈空;当top != -1时,栈非空.

cpp 复制代码 
#include <iostream>
using namespace std;
using ElemType = int;

#define MaxSize 10

typedef struct {
	ElemType data[MaxSize];     //静态数组存放栈中元素
	int top;     //栈顶指针

}SqStack;

//初始化栈
void InitStack(SqStack& S) {
	S.top = -1;
}

//判断栈空
bool StackEmpty(SqStack S) {
	if (S.top = -1) {
		return true;
	}
	else
		return false;
}

int main() {
	SqStack S;
	InitStack(S);
	cout << (StackEmpty(S) ? "栈空" : "栈非空") << endl;
}

三.进栈,出栈操作

1.进栈操作

现在内存中有a元素, top指向data[0], 即top = 0;

如果想在a后面插入一个元素b, 则需要先将top值 + 1, 再将b填入data[1]中;
用代码表示为:

S.top = S.top + 1;

S.data[S.top] = x;
等价于:

S.data[++S.top] = x;
注意:

是"++S.top"不是"S.top++"

入栈不要忘记判断栈满(栈满不能进)

cpp 复制代码 
//新元素入栈
bool Push(SqStack& S, ElemType x) {
	if (StackFull(S)) {
		return false;
	}
	S.top = S.top + 1;     //指针先加1
	S.data[S.top] = x;     //新元素入栈
	//等价于: 
    S.data[++S.top] = x;
	return true;
}
2.出栈操作

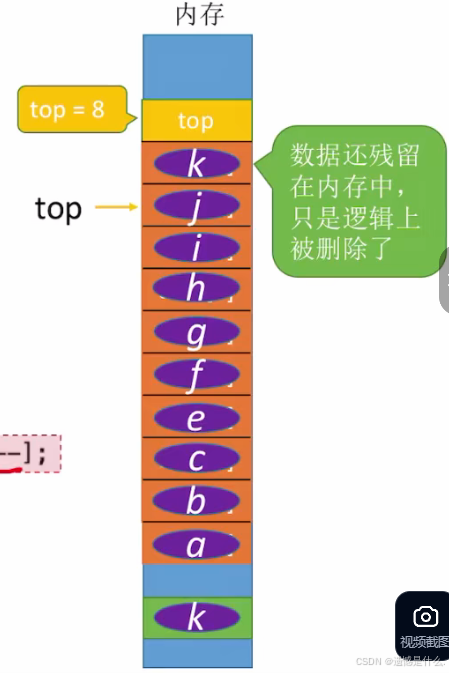现在内存中存在10个元素, 现在要将栈顶元素k删除, 需要在内存中留一个ElemType x的内存空间,

然后将k复制到该位置;

现在将data[9]位置的k删去,即top指向data[8],即top = 8:x = S.data[S.top];

再将top-1:S.top = S.top - 1;
等价于:

x = S.data[S.top--];
注意:

是"S.top--"而不是"--S.top"

出栈不要忘记判断栈空(空栈不能出)

cpp 复制代码 
//出栈
bool Pop(SqStack& S, ElemType& x) {
	if (StackEmpty(S)) {
		return false;
	}
	x = S.data[S.top];
	S.top = S.top - 1;
	//等价于: x = S.data[S.top--];
	return true;
}
3.读栈顶元素
cpp 复制代码 
// 出栈操作
bool Pop(SqStack &S, ElemType &x) {
    if (S.top == -1)         // 栈空，报错
        return false;
    x = S.data[S.top--];     // 先出栈，指针再减1
    return true;
}

// 读栈顶元素
bool GetTop(SqStack S, ElemType &x) {
    if (S.top == -1)        // 栈空，报错
        return false;
    x = S.data[S.top];      // x 记录栈顶元素
    return true;
}

出栈操作和读栈顶元素的操作的区别:出栈操作指针需要减一,top--;

4.完整代码
cpp 复制代码 
#include <iostream>
using namespace std;
using ElemType = int;
#define MaxSize 10

typedef struct {
	ElemType data[MaxSize];
	int top;
}SqStack;

void InitStack(SqStack& S) {
	S.top = -1;
}

//栈空
bool StackEmpty(SqStack S) {
	if (S.top == -1) {
		return true;
	}
	else
		return false;
}

//栈满
bool StackFull(SqStack S) { 
	if (S.top == MaxSize - 1) {
		return true;
	}
	else {
		return false;
	}
}

//入栈
bool Push(SqStack& S, ElemType x) {
	if (StackFull(S)) {
		return false;
	}
	S.top = S.top + 1;     //指针先加1
	S.data[S.top] = x;     //新元素入栈
	//等价于: S.data[++S.top] = x;
	return true;
}

//出栈
bool Pop(SqStack& S, ElemType& x) {
	if (StackEmpty(S)) {
		return false;
	}
	x = S.data[S.top];
	S.top = S.top - 1;
	//等价于: x = S.data[S.top--];
	return true;
}

//读栈顶
bool GetTop(SqStack& S, ElemType& x) {
	if (StackEmpty(S)) return false;
	x = S.data[S.top];
	return true;
}


/*----------------  测试  ----------------*/
int main() {
	SqStack S;
	InitStack(S);

	for (int i = 1; i <= MaxSize + 1; ++i)          // 故意多 push 一次
		if (!Push(S, i))
			cout << "第" << i << "次入栈失败（栈满）\n";

	ElemType x;
	while (Pop(S, x))
		cout << x << " 出栈\n";

	return 0;
}
5.注意问题

(1) 区别:

cpp 复制代码 
//入栈
bool Push(SqStack& S, ElemType x)

//出栈
bool Pop(SqStack& S, ElemType& x)

1.
形参里的 & 位置不同

Push 只有 栈 带 & ： SqStack& S

Pop 除了 栈 带 & ，还多了 出栈元素 的 & ： ElemType& x
2.
作用不同

Push 把 x 的值"复制"进栈，不需要 改 x ，所以 x 按值传递。

Pop 要把栈顶值"送"给调用者，必须 改 x ，所以 x 按引用传递。

一句话：
" Push 只改栈， Pop 既要改栈又要改调用者的变量，因此多一个 & 。"

(2): StackEmpty 和 StackFull 里把"比较"写成了"赋值"：

cpp 复制代码 
//栈空
bool StackEmpty(SqStack S) {
	if (S.top == -1) {
		return true;
	}
	else
		return false;
}

//栈满
bool StackFull(SqStack S) { 
	if (S.top == MaxSize - 1) {
		return true;
	}
	else {
		return false;
	}
}

S.top 是和 -1,MaxSize-1 比较的,而不是复制,这里使用"=="而不是"=".

6.另一种方式

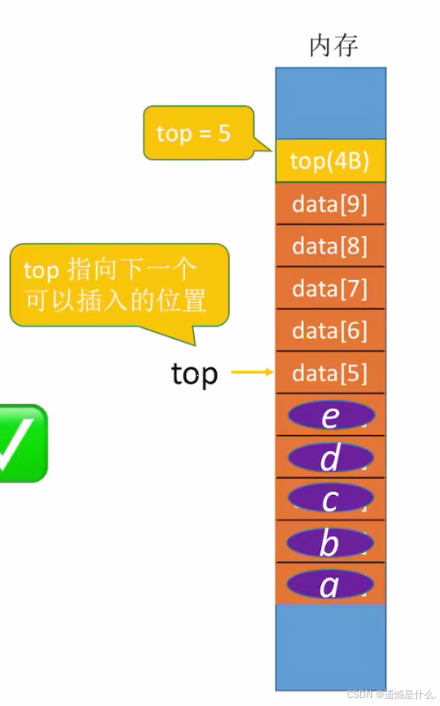另一种进栈的方式:

top指向下一个可以插入的位置, 如图在e元素后面插入元素, 直接让top指向data[5],

此时添加元素则要先填入x, 再top++;
进栈代码为:

S.data[S.top] = x;

S.top = S.top + 1;
等价于:

S.data[S.top++] = x;
出栈代码为:

S.top = S.top - 1;

x = S.data[S.top];
等价于:

x = S.data[--S.top];

四.共享栈

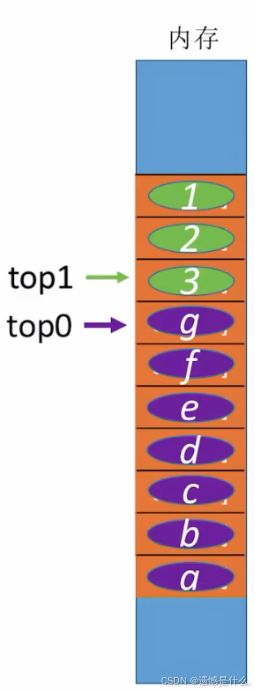定义:

两个栈共享同一片内存空间,两个栈从两边往中间增长
初始化:

0号栈栈顶指针初始化时 top0 = -1;

1号栈栈顶指针初始化时 top1 = MaxSize;
栈满条件:

top0 + 1 == top1;

cpp 复制代码 
#include <iostream>
using namespace std;

constexpr int MaxSize = 10;
using ElemType = int;

/*---------- 共享栈结构 ----------*/
struct ShStack {
    ElemType data[MaxSize];
    int top0;   // 左栈顶，空时为 -1
    int top1;   // 右栈顶，空时为 MaxSize
};

/*---------- 基本操作 ----------*/
void InitStack(ShStack &S) {
    S.top0 = -1;
    S.top1 = MaxSize;   // 原代码缺分号，已补
}

bool Stack0Empty(const ShStack &S) { return S.top0 == -1; }
bool Stack1Empty(const ShStack &S) { return S.top1 == MaxSize; }
bool StackFull(const ShStack &S)  { return S.top0 + 1 == S.top1; }

/* 左栈进栈 */
bool Push0(ShStack &S, ElemType x) {
    if (StackFull(S)) return false;
    S.data[++S.top0] = x;
    return true;
}

/* 右栈进栈 */
bool Push1(ShStack &S, ElemType x) {
    if (StackFull(S)) return false;
    S.data[--S.top1] = x;
    return true;
}

/* 左栈出栈 */
bool Pop0(ShStack &S, ElemType &x) {
    if (Stack0Empty(S)) return false;
    x = S.data[S.top0--];
    return true;
}

/* 右栈出栈 */
bool Pop1(ShStack &S, ElemType &x) {
    if (Stack1Empty(S)) return false;
    x = S.data[S.top1++];
    return true;
}

/*---------- 测试 ----------*/
int main() {
    ShStack S;
    InitStack(S);

    for (int i = 1; i <= 6; ++i) Push0(S, i);   // 左栈：1 2 3 4 5 6
    for (int i = 10; i >= 7; --i) Push1(S, i);  // 右栈：10 9 8 7

    ElemType x;
    while (!Stack0Empty(S)) { Pop0(S, x); cout << "左栈出: " << x << '\n'; }
    while (!Stack1Empty(S)) { Pop1(S, x); cout << "右栈出: " << x << '\n'; }
    return 0;
}

五.知识回顾

六.链栈的增,删,查(栈顶元素)操作

cpp 复制代码 
#include <iostream>
using namespace std;

using ElemType = int;

/*---------- 结点定义 ----------*/
struct StackNode {
    ElemType data;
    StackNode* next;
};

/*---------- 1. 初始化 ----------*/
void InitStack(StackNode*& S) {   // 引用指针，调用后 S 为 nullptr
    S = nullptr;                  // 不带头结点，空栈时栈顶就是 nullptr
}

/*---------- 2. 判空 ----------*/
bool StackEmpty(StackNode* S) {
    return S == nullptr;
}

/*---------- 3. 入栈（增）----------*/
bool Push(StackNode*& S, ElemType x) {
    StackNode* p = new StackNode;   // 新建结点
    if (!p) return false;           // 内存分配失败
    p->data = x;
    p->next = S;                    // 头插法
    S = p;                          // 更新栈顶
    return true;
}

/*---------- 4. 出栈（删）----------*/
bool Pop(StackNode*& S, ElemType& x) {
    if (StackEmpty(S)) return false;
    StackNode* p = S;               // 暂存栈顶结点
    x = p->data;
    S = S->next;                    // 栈顶下移
    delete p;                       // 释放原栈顶
    return true;
}

/*---------- 5. 获取栈顶元素（查）----------*/
bool GetTop(StackNode* S, ElemType& x) {
    if (StackEmpty(S)) return false;
    x = S->data;
    return true;
}

/*---------- 6. 测试 ----------*/
int main() {
    StackNode* S;
    InitStack(S);

    for (int i = 1; i <= 5; ++i) Push(S, i);   // 入栈 1 2 3 4 5

    ElemType x;
    while (!StackEmpty(S)) {
        GetTop(S, x);
        cout << "栈顶: " << x << "  ";
        Pop(S, x);
        cout << "出栈: " << x << '\n';
    }
    return 0;
}
相关推荐
清风er2 小时前
智能座舱开发
算法·计算机视觉
Learn Beyond Limits2 小时前
Data Mining Tasks｜数据挖掘任务
人工智能·python·神经网络·算法·机器学习·ai·数据挖掘
liuhuapeng03042 小时前
GetMapping自动截取List＜String＞字符
数据结构·windows·list
Croa-vo2 小时前
Citadel SDE 面试复盘：直面硬核算法与思维挑战的双重压力
算法·面试·职场和发展
仰泳的熊猫2 小时前
1013 Battle Over Cities
数据结构·c++·算法·pat考试
_OP_CHEN3 小时前
算法基础篇：（七）基础算法之二分算法 —— 从 “猜数字” 到 “解难题” 的高效思维
c++·算法·蓝桥杯·二分查找·acm·二分答案·二分算法
一匹电信狗3 小时前
【C++11】Lambda表达式+新的类功能
服务器·c++·算法·leetcode·小程序·stl·visual studio
在等晚安么3 小时前
力扣面试150题打卡
算法·leetcode·面试
AI科技星4 小时前
宇宙膨胀速度的光速极限：基于张祥前统一场论的第一性原理推导与观测验证
数据结构·人工智能·经验分享·python·算法·计算机视觉
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03Linux下V2Ray安装配置指南04安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）05综合整理：pdf预览显示：你尝试预览的文件可能对你的计算机有害。如果你信任此文件以及其来源，请打开此文件以看其内容，如何解决以正常预览文件06Labelme从安装到标注：零基础完整指南07BongoCat - 跨平台键盘猫动画工具08智能库存管理的需求预测模型：从业务痛点到落地代码的完整实践09《大数据技术原理与应用》实验报告三 熟悉HBase常用操作10全面评测 | Photoshop 2026 新特性深度解析与实测体验