二分查找算法介绍及使用

[1. 什么是二分查找](#1. 什么是二分查找)

[2. 二分查找的逻辑](#2. 二分查找的逻辑)

[什么是二分查找的 "二段性"？](#什么是二分查找的 “二段性”？)

[3. 例题讲解演示](#3. 例题讲解演示)

[3.1 LeetCode704. 二分查找](#3.1 LeetCode704. 二分查找)

[3.2 LeetCode852. 山脉数组的峰顶索引](#3.2 LeetCode852. 山脉数组的峰顶索引)

[3.3 LeetCode69. x 的平方根](#3.3 LeetCode69. x 的平方根)

[3.4 LeetCode34. 在排序数组中查找元素的第一个和最后一个位置](#3.4 LeetCode34. 在排序数组中查找元素的第一个和最后一个位置)

今天我们来聊一聊二分查找算法。

1. 什么是二分查找

分查找（Binary Search）是一种针对有序集合 的高效查找算法，核心思想是通过不断将查找范围减半来快速定位目标元素。其前提是集合必须按某种规则排序，每次通过比较中间元素与目标值的大小，缩小查找范围，直到找到目标或范围为空。

时间复杂度为 O(log n)（n 为集合长度），远优于线性查找的 O (n)，适用于静态有序数据的快速查询。

二分查找的效率很高，因为他每次都可以直接排除掉一半的数据。

2. 二分查找的逻辑

二分查找的本质就是通过找到数组的二段性，然后每次筛选一半的方式来快速查找。

我们要了解二分查找的逻辑，那么我们就先要了解什么是二段性。

什么是二分查找的 "二段性"？

"二段性" 是二分查找的核心本质，指待查找的集合可以被某个条件划分为 "满足条件" 和 "不满足条件" 的两个连续区间，且这两个区间具有明确的边界。

简单来说：

整个集合被分为两部分，前半部分（或左半部分）全部满足某个条件，后半部分（或右半部分）全部不满足（反之亦然）。
二分查找的过程，本质上是通过不断判断中间元素属于哪一段，来缩小范围，最终找到两段的边界（或目标元素）。

给各位句几个简单的例子，我们看下面这个图，如果我们要查找的是3，那么它的二段性就是大于3的数和小于3的数。我们通过不断筛选，最后找到3。

我们看下面这个图，那么我们该如何找到这组数里面最大的。如果只知道二分查找可以使用到有序数组的话，我们在下面这个图里面是想不到使用二分查找的。那么我们该怎么使用二分查找呢，或者说二段性该如何理解呢？很简单，它的二段性就是上升期的数和下降期的数。这样我们就可以找到里面最大的。

3. 例题讲解演示

接下来我们通过讲解几道例题的方式来帮助大家理解二分查找。

3.1 LeetCode704. 二分查找

我们看下面这个图片，这个的话就是很普通的二分查找例题。就是要求我们从一个有序的数组里面找到要求的数字，如果那个数字不在数组里面的话，那就返回-1。

它的二段性就是比它大的值和比它小的值。

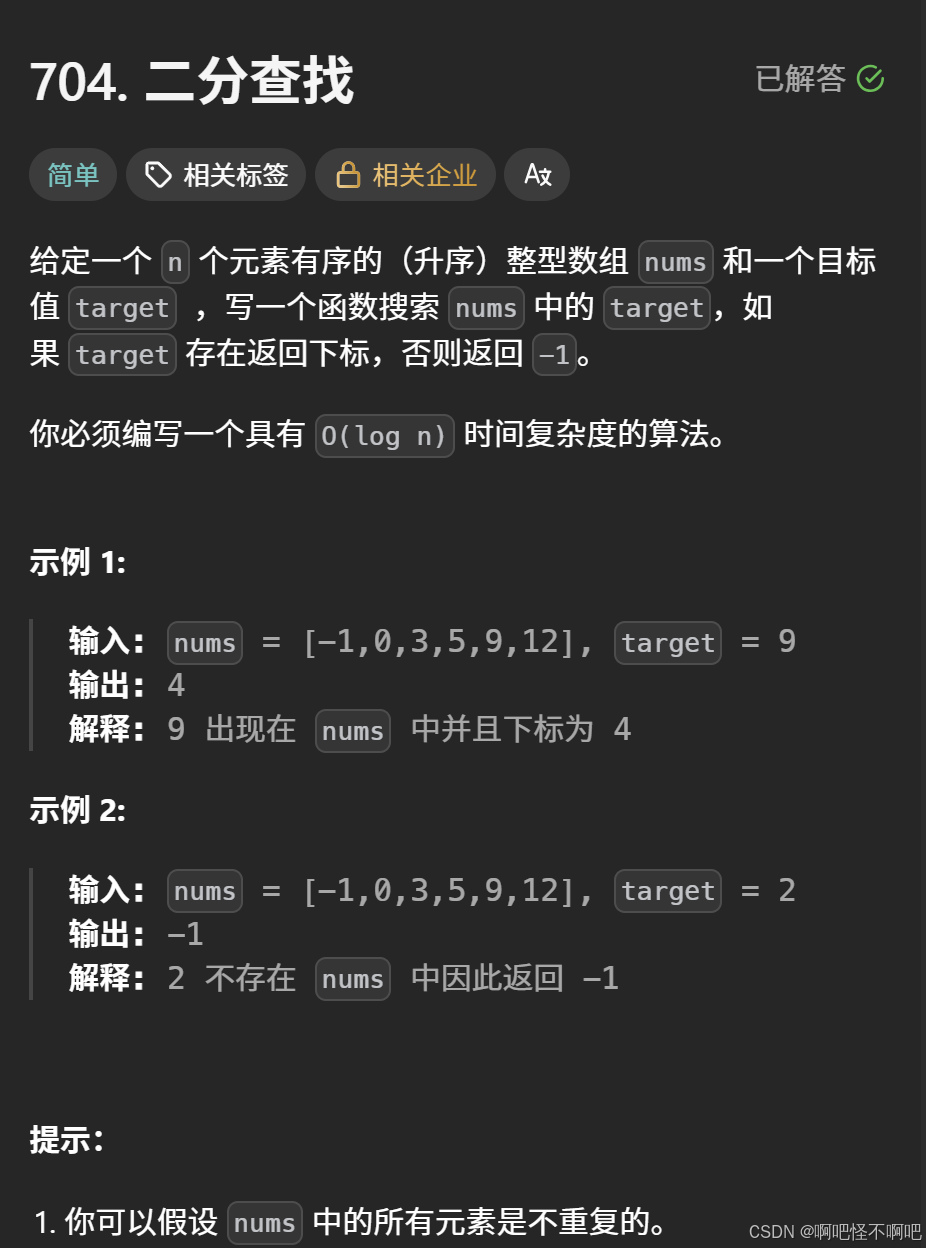
我们看下面的代码，就是先设置一个l和一个r，分别指向数组的最左边和最右边，接着再根据l+（r-l）/2计算出mid，也就是中间位置的下标。接着我们拿这个位置的下标对应的值去和目标值作比较，如果相等就直接结束，否则就把l或者r更新为mid。

这个while循环里面的条件很好理解，如果l>r了那么就说明没有找到，所以直接返回-1。

cpp 复制代码

class Solution {
public:
    int search(vector<int>& nums, int t) {
        int sz=nums.size();
        int l=0;
        int r=sz-1;
        while(l<=r)
        {
            int mid=l+(r-l)/2;
            if(nums[mid]>t)
                r=mid-1;
            else if(nums[mid]<t)
                l=mid+1;
            else
            {
                return mid;
            }
        }
        return ;
    }
};

3.2 LeetCode852. 山脉数组的峰顶索引

我们接着看下面这一道题，这道题就是我上面说的那种找最大值。

它的二段性就是上升期的数和下降期的数。

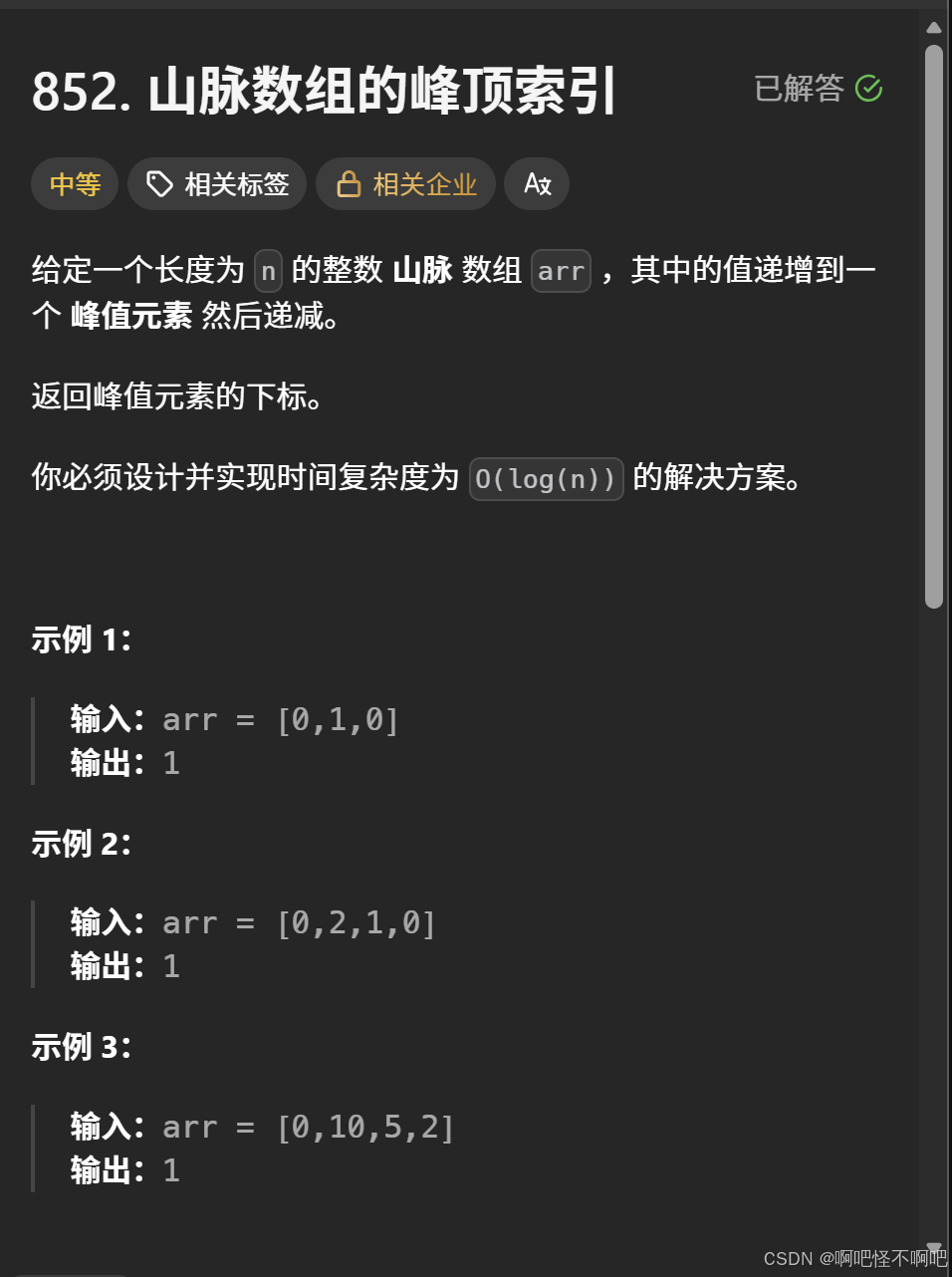
我们看下面这个代码，其实很多地方也是差不多的，唯一的区别就是把两个条件判断给修改一下。

因为要判断是上升期的数还是下降期的数，所以我们要和和周围的数去比较。

cpp 复制代码

class Solution {
public:
    int peakIndexInMountainArray(vector<int>& arr) {
        int sz=arr.size();
        int l=0;
        int r=sz-1;
        while(l<r)
        {
            int m=l+(r-l+1)/2;
            if(arr[m-1]<arr[m])
                l=m;
            else if(arr[m-1]>arr[m])
                r=m-1;
        }
        return r;
    }
};

3.3 LeetCode69. x 的平方根

我们来看下面这道题，这道题同样也可以使用二分查找算法。题目意思很简单，要求我们找出一个数的算术平方根。

它的二段性就是和自己相乘后比x要大的数和比x要小的数。

因为算术平方根就是一个数开根号后的结果，所以我们这边直接通过设立边界，然后查找哪个数的值和自己相乘的结果等于x。

如果没有拿到我们想要的也没有事，因为当l>r时的那个值就是去除小数后的结果。

cpp 复制代码

class Solution {
public:
    int mySqrt(int x) {
        int l=0;
        int r=x;
        if(x<2)
            return x;
        while(l<=r)
        {
            long long mid=l+(r-l)/2;
            if(mid*mid>x)
                r=mid-1;
            else if(mid*mid<x)
                l=mid+1;
            else
                return mid;
        }
        return r;
    }
};

3.4 LeetCode34. 在排序数组中查找元素的第一个和最后一个位置

这道题的目的是让各位了解到二分查找使用上的广泛性。

这道题稍微有一点难，题目意思就是说给一个值，然后要求我们找到数组里面这个数出现的起始位置和结尾位置。如果数组里面没有这个数的话就直接返回 $-1,-1$ 。

这道题的二段性比较特殊，放在下面的代码解析那里说。

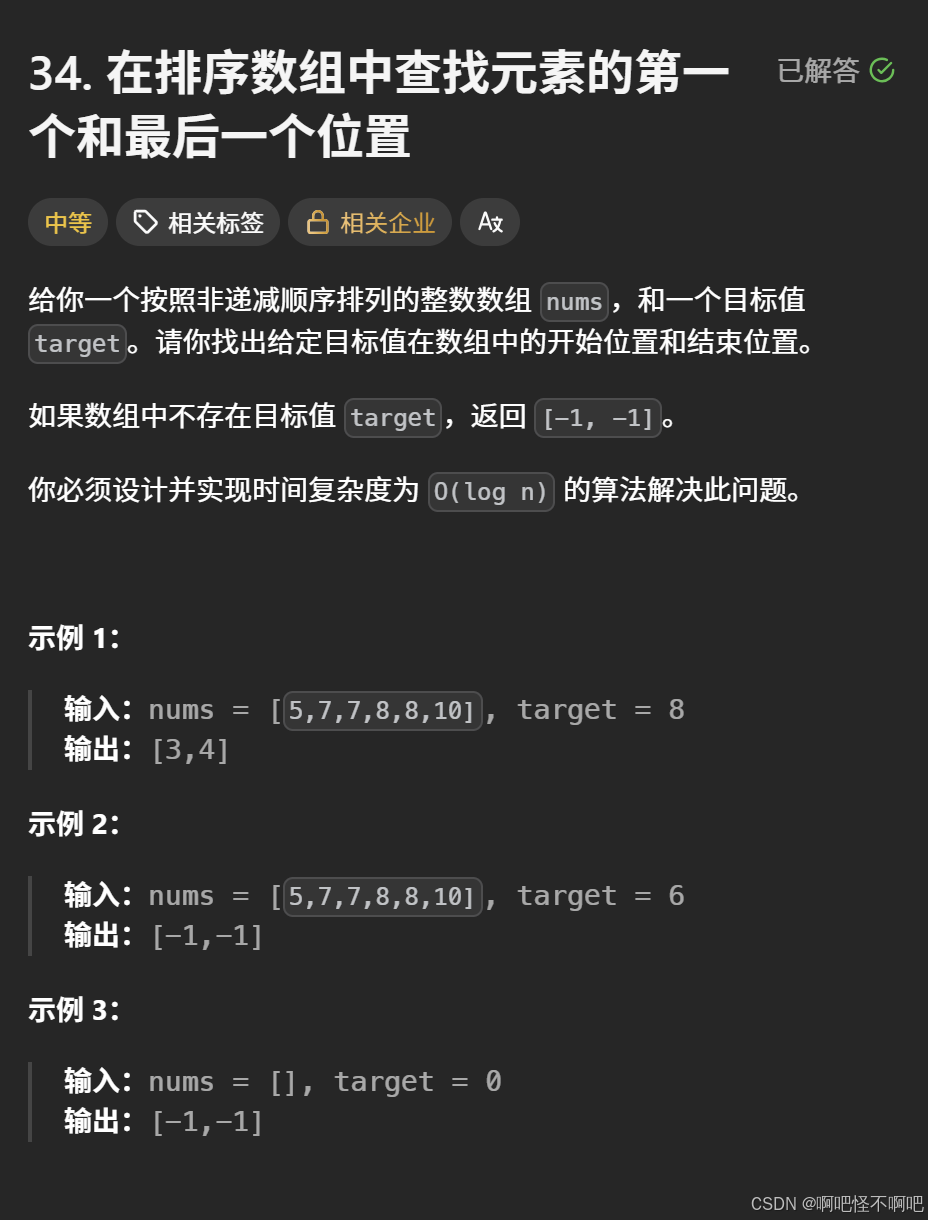
这道题我们可以理解为使用两次二段性，首先我们通过二段性查找t值在数组中的起始位置，也就是左边界，二段性为左边全是比要求小的值，右边为等于或大于要求的值。接着我们查找结尾位置，也就是右边界，二段性为右边全是比要求大的值，右边为等于或小于要求的值。这样我们就找到了左右边界，这样我们就做完了这道题。

cpp 复制代码

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int t) {
        int sz=nums.size();
        int l=0;
        int r=sz-1;
        int begin=0;
        int end=0;
        if(sz==0)
            return {-1,-1};
        //找左
        while(l<r)
        {
            int m=l+(r-l)/2;
            if(nums[m]>=t)
                r=m;
            else if(nums[m]<t)
                l=m+1;
        }
        if(nums[l]!=t)
            return {-1,-1};
        else
            begin=l;
        //找右
        l=0;
        r=sz-1;
        while(l<r)
        {
            int m=l+(r-l+1)/2;
            if(nums[m]>t)
                r=m-1;
            else if(nums[m]<=t)
                l=m;
        }
        end=r;
        return {begin,end};
    }
};