C++ 面试高频考点 链表 迭代 递归 力扣 25. K 个一组翻转链表 每日一题 题解

文章目录

• 零、题目描述
• 一、为什么这道题值得你花时间弄懂？
• 二、算法原理
• 三、代码实现
• • 迭代实现
  • • 迭代实现的易错点
    • 迭代实现的优缺点
  • 递归实现
  • • 思路差异补完
    • 递归实现的易错点
    • 递归实现的优缺点
• 四、总结
• • 两种实现对比（表格）
  • 关键考点与避坑点
  • 核心思想迁移
• 五、下题预告

零、题目描述

题目链接：力扣 25. K 个一组翻转链表

题目描述：

示例 1：

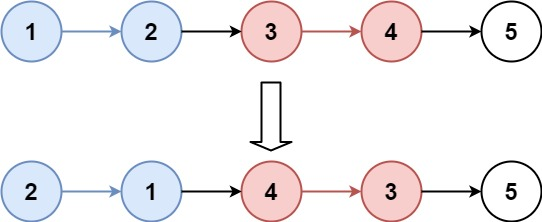
输入：head = [1,2,3,4,5], k = 2

输出：[2,1,4,3,5]

解释：

将前 2 个节点翻转 → [2,1]，中间 2 个节点翻转 → [4,3]，最后 1 个节点保持不变，最终拼接为 [2,1,4,3,5]
示例 2：

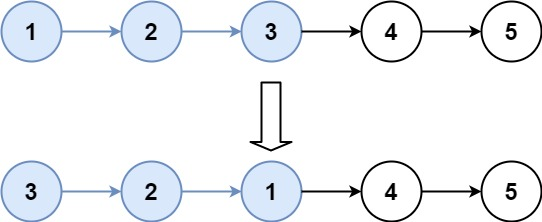
输入：head = [1,2,3,4,5], k = 3

输出：[3,2,1,4,5]

解释：

前 3 个节点翻转 → [3,2,1]，剩余 2 个节点保持不变，最终拼接为 [3,2,1,4,5]
示例 4：

输入：head = [], k = 1

输出：[]
提示：

链表中的节点数目为 n，

1 <= k <= n <= 5000，

0 <= Node.val <= 1000

一、为什么这道题值得你花时间弄懂？

"K个一组翻转链表"是链表操作的进阶核心题，更是面试中区分"基础选手"和"进阶选手"的高频考点，难度直接拉满但价值极高。

题目核心价值

这道题之所以成为面试"拦路虎"，本质是它能全面考察链表操作的硬实力，覆盖企业最看重的核心能力：

• 多步操作协同能力：需同时处理"局部翻转""区间衔接""剩余节点保留"三大核心需求，步骤环环相扣，一步错则满盘错；
• 指针操作精准度：链表翻转本身就是指针操作的经典场景，而"K个一组"要求在多组翻转中精准控制游标指针，是考察"指针敏感度"的最佳载体；
• 边界与细节把控：节点总数不是k的整数倍时的处理、最后一组不翻转的判断、空链表/单节点链表的兼容，这些细节正是面试丢分重灾区；
• 算法思维灵活性：支持递归和迭代两种主流实现，能考察你对"分治思想"（递归）和"循环控制"（迭代）的灵活运用，面试官常追问两种解法的优劣对比。

面试考察的核心方向

1. 能否快速梳理出"分组-翻转-衔接"的核心流程，避免逻辑混乱；
2. 递归实现中，能否准确设计递归终止条件和子问题边界；
3. 迭代实现中，能否用指针标记关键节点（如每组头/尾、前驱/后继），避免衔接断裂；
4. 面对特殊测试用例（k=1、k=n、空链表）时，代码是否稳健；
5. 能否清晰分析两种实现的时间/空间复杂度，并有针对性地选择最优解法。

掌握这道题，相当于彻底攻克链表操作的"进阶关卡"，后续遇到链表拆分、重组等复杂问题都能举一反三，面试中再遇链表难题也能从容应对。

二、算法原理

1.处理链表逆序轮数

这道题我的思路就是，先将链表总长度求出来，这样我们就可以求出一共要反转多少组，这样我们就可以将一个大问题变成重复若干次长度为K个的链表逆序，这就像切蛋糕，得先知道蛋糕总共有多大，才能确定能切成几块一样。具体怎么做呢？

很简单，咱们先把整个链表完整遍历一遍，数一数节点的总数，记为size------这就是链表的"总长度"。接下来，用size/K，得到的结果就是咱们需要重复反转的"轮数"；而size % K算出来的余数，就是最后那段"不需要反转"的链表长度，但是这部分最后直接接在结果后面就行，不用额外处理。

2.头插逆序链表

搞定了"要反转多少轮"，接下来就是核心步骤：重复n轮"每段K个节点的反转"。这里我用的是特别好上手的"头插法"，而且只要创建一个虚拟头节点 ，就能轻松搞定反转过程，一点都不绕，如下图👇：

※3.如何链接？※

头插的原理我们弄懂之后，有个关键问题：每反转完一组，怎么和下一组"无缝衔接"呢？

咱们结合例子看更清楚。比如原链表是像图里那样的结构👇：

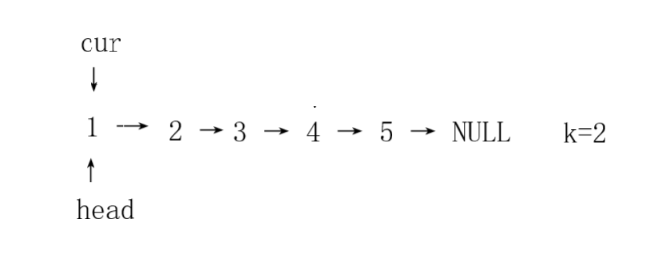
当我们反转完第一组后会发现：原本第一组的"头节点"，现在变成了第一组的"尾节点"，而这个尾节点，正好是第二组的"前驱节点"------相当于它成了两组之间的"连接桥"。

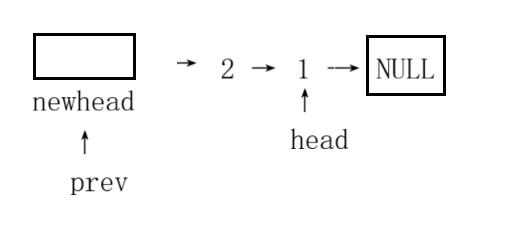
那么我们可以根据这个启发，定义一个指针指向每组的第一个，当逆序后就会成为本组的尾节点，也就是下一组的前驱节点。但这里要注意，不能直接用一开始的head指针当这个"连接桥"，因为head只在第一组有效，到了后面的组就会"错位"。

所以我们定义一个指针，让它始终指向"当前要反转组的前驱节点"。比如反转第一组时，这个指针先指向虚拟头节点；反转完第一组后，它就更新成第一组的尾节点（也就是原来第一组的头节点），这样下一组反转时，就能通过它和上一组牢牢连在一起。

当我们逆序好一组之后我们就可以通过这个节点与上一组进行链接，具体就是我们将下一组头插的头节点指针更新成我们的前驱节点指针指向的位置，之后前驱节点更新成这一组的第一个节点的位置，这样新的一组就会以这个头插的头节点指针进行逆序，如下图👇：

其实这部分是整个题的"关键细节"，光听文字描述可能会有点抽象。大家可以结合GIF图里的过程，或者自己在纸上画一画每一步的指针变化------比如先画原链表，再标出指针走一遍，很快就能get到其中的逻辑啦～

---

三、代码实现

其实通过算法原理那里大家也可以发现，这道题递归和迭代都可以实现，下面我写了两个方式实现代码，和大家一起理解并补充再算法原理没有提到的代码实现上的细节，并说明递归实现思路上与我上述的算法原理的差异。

注：我上面的算法原理其实是迭代的，因为递归的思路比迭代的清晰，我就着重以迭代的思路进行分析讲解了

迭代实现

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseKGroup(ListNode* head, int k) {
        int size = 0;
        ListNode* tmp = head;
        // 统计链表总长度
        while(tmp != nullptr)
        {
            size++;
            tmp = tmp->next;
        }
        // 计算可完整翻转的组数
        int n = size/k;

        ListNode* newhead = new ListNode();  // 哨兵节点，统一处理链表头部
        ListNode* prev = newhead;  // 前驱指针：指向当前组的前一个节点（用于衔接）
        ListNode* cur = head;      // 当前指针：指向当前组的第一个节点

        // 迭代处理每一组
        for(int i = 0; i < n; i++)
        {
            ListNode* mark = cur;  // 标记当前组的原头节点（翻转后变为尾节点）
            // 头插法翻转当前组k个节点
            for(int j = 0; j < k; j++)
            {
                ListNode* next = cur->next;  // 保存当前节点的下一个节点
                cur->next = prev->next;      // 头插法核心：当前节点指向前驱的下一个节点
                prev->next = cur;            // 前驱指向当前节点，完成插入
                cur = next;                  // 移动到下一个待翻转节点
            }
            prev = mark;  // 更新前驱指针为当前组的尾节点（供下一组衔接）
        }

        // 衔接剩余未翻转的节点
        prev->next = cur;
        ListNode* result = newhead->next;  // 最终结果的头节点（跳过哨兵）
        delete newhead;  // 释放哨兵节点，避免内存泄漏

        return result;
    }
};

迭代实现的易错点

1. 前驱指针更新错误：每组翻转后未将 prev 指向当前组的尾节点，会导致下一组翻转后无法衔接。
2. 当前指针越界：翻转组内节点时，未正确保存 cur->next 就移动指针，会导致节点丢失。
3. 剩余节点衔接遗漏：忘记将最后一组的尾节点指向剩余未翻转节点，会导致链表尾部断裂。
4. 哨兵节点使用不当：未通过哨兵节点统一处理头部，可能导致第一组翻转后头节点错误。

迭代实现的优缺点

• 优点：空间复杂度为O(1)（仅使用常数级指针变量），无递归栈溢出风险，更适合大规模数据；
• 缺点：逻辑相对复杂，需要手动标记前驱、当前组头尾等多个指针，对指针操作的精准度要求更高。

递归实现

思路差异补完

在算法原理也就是迭代实现那里，我们衔接两个部分的链表是用一个前驱指针更新头插指针的位置，让每一次头插都在newhead的最后面，但是递归不用那么麻烦，我们递归函数的作用就是将逆序后的链表的头节点返回给当前层，那么我们将当前层逆序之后head直接就是尾指针就可以直接进行连接。在这道题中自下而上思路相较于自上而下的更加简洁易懂。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseKGroup(ListNode* head, int k) {
        int size = 0;
        ListNode* tmp = head;
        // 统计链表总长度，判断分组翻转条件
        while(tmp != nullptr)
        {
            size++;
            tmp = tmp->next;
        }
        // 调用递归函数，传入头节点、k值和剩余节点数
        return List(head,k,size);
    }

    // 递归函数：翻转当前组，返回翻转后的组头节点
    ListNode* List(ListNode* head, int k, int size) {
        // 递归终止条件：剩余节点数不足k，直接返回当前头节点（无需翻转）
        if(size < k)
            return head;
        
        // 找到下一组的起始节点（当前组第k+1个节点）
        ListNode* cur1 = head;
        int num = k;
        while(num)
        {
            cur1 = cur1->next;
            num--;
            size--;
        }
        // 递归处理下一组，得到下一组翻转后的头节点
        ListNode* ret = List(cur1,k,size);

        // 头插法翻转当前组k个节点
        ListNode* newhead = new ListNode();  // 临时哨兵节点，简化翻转操作
        ListNode* cur = head;
        num = k;
        while(num)
        {
            ListNode* next = cur->next;  // 保存当前节点的下一个节点
            cur->next = newhead->next;   // 头插法核心：当前节点指向哨兵节点的下一个节点
            newhead->next = cur;         // 哨兵节点指向当前节点，完成插入
            cur = next;                  // 移动到下一个待翻转节点
            num--;
        }
        
        // 衔接当前组和下一组：当前组原头节点（翻转后变为尾节点）指向后一组头节点
        head->next = ret;
        ListNode* result = newhead->next;  // 保存当前组翻转后的头节点
        delete newhead;  // 释放哨兵节点，避免内存泄漏

        return result;  // 返回当前组翻转后的头节点，供上一层递归衔接
    }
};

递归实现的易错点

1. 剩余节点数计算错误：递归传递 size 时，我们需准确减去当前组的k个节点，否则会导致重复翻转或漏翻转。
2. 组间衔接断裂：忘记将当前组翻转后的尾节点（原头节点）指向后一组头节点，会导致链表断开。
3. 哨兵节点内存泄漏：创建临时哨兵节点后未释放，长期运行会导致内存溢出。
4. 递归终止条件模糊：未明确"剩余节点数 < k"时直接返回，可能导致多组翻转逻辑混乱。

递归实现的优缺点

• 优点：逻辑清晰，通过递归自然拆分"当前组"和"后续组"，无需手动标记组间关系，代码简洁；
• 缺点：递归深度为 m = n/k，当n较大时（如n=5000、k=1），递归栈可能溢出；空间复杂度为O(m)，高于迭代实现。

---

四、总结

两种实现对比（表格）

实现方式	时间复杂度	空间复杂度	核心优势	适用场景
递归	O(n)	O(n/k)	逻辑清晰，代码简洁，无需手动衔接组间关系	面试快速编码、追求逻辑简洁性
迭代	O(n)	O(1)	空间最优，无栈溢出风险	生产环境、大规模链表场景

关键考点与避坑点

• 长度统计：必须先统计链表长度，避免对不足k个的节点组进行翻转；
• 指针控制：无论是递归还是迭代，都需精准保存"下一个节点"，避免指针丢失导致链表断裂；
• 组间衔接：核心是找到每组翻转后的尾节点（原头节点），并指向后一组的头节点；
• 哨兵节点：合理使用哨兵节点可简化头节点处理和翻转操作，但需注意释放内存；
• 特殊用例：k=1（无需翻转）、k=n（整表翻转）、空链表，需确保代码兼容。

核心思想迁移

• 局部翻转：可迁移至"链表指定区间翻转""两两交换链表节点"等问题；
• 分组处理：可迁移至"链表分段操作"（如分段排序、分段删除）；
• 指针标记技巧：前驱、当前、后继指针的控制逻辑，是所有复杂链表操作的核心基础。

五、下题预告

链表相关的核心操作我们就暂告一段落啦，下一次我们将开启哈希表的学习之旅，我们会用 力扣 1. 两数之和 这道 "典中典" 题目，从零拆解哈希表的核心逻辑、使用场景和解题技巧，一步步攻克这类高频面试题！

Doro 带着小花🌸来啦！🌸奖励🌸坚持啃下这道链表硬骨头的你！"K 个一组翻转链表" 确实不容易，既要处理局部翻转，又要兼顾组间衔接，能写出递归和迭代两种实现，已经超棒啦～

相信现在的你，对链表指针操作和分组处理的逻辑已经了如指掌，下次面试再遇到这类问题，一定能快速理清思路，精准写出代码。把这篇内容收藏起来，后续刷题时遇到链表翻转、分段操作的题目，随时翻查就能快速唤醒记忆。

关注博主，下一篇我们就攻克哈希表入门，把 "用空间换时间" 的解题思维彻底掌握！如果你在今天的学习中有任何疑问 ------ 比如递归终止条件的设计、迭代中指针的标记逻辑，或者有更优的解题思路，都可以发到评论区，博主看到会第一时间回复。

最后别忘了点个赞呀，你的支持就是博主持续更新优质算法内容的最大动力，我们下道题不见不散！

要不要我帮你整理一份两种实现的核心代码对比表，清晰标注关键差异和易错点，方便你快速复习？