K-means 聚类是一种无监督机器学习算法,核心是将数据集自动划分为 K 个互不重叠的簇,使每个簇内数据相似度高、簇间相似度低。
一、核心原理
基于 "距离度量" 实现簇的划分,
常用欧氏距离衡量数据点间的相似度,
最终目标是最小化所有簇的 "簇内平方和(SSE)",
即每个数据点到其所属簇中心的距离平方和。
二、算法核心步骤
- 确定簇数 K(需人工预设或通过肘部法则等方法选择)。
- 随机选择 K 个数据点作为初始簇中心。
- 计算每个数据点到所有簇中心的距离,将其分配到距离最近的簇。
- 重新计算每个簇的均值(即新的簇中心)。
- 重复步骤 3-4,直到簇中心不再明显变化或达到预设迭代次数。
①K-means 算法的实现步骤
算法流程可概括为 "初始化→分配→更新→收敛" 四步,具体如下:
1. 初始化:确定簇数 K 并选择初始簇中心
- 输入:数据集 X={x1,x2,...,xn}(xi 为 d 维特征向量),预设簇数 K。
- 操作:从数据集中随机选择 K 个样本作为初始簇中心 μ1,μ2,...,μK(μk 为第 k 个簇的中心,也是 d 维向量)。
2. 分配:将样本分配到最近的簇
- 目标:对每个样本 xi,计算它与所有簇中心 μk 的距离,将其分配到距离最近的簇。
- 操作:为每个样本 xi 定义一个 "簇分配标签" ci,其中 ci∈{1,2,...,K},表示 xi 属于第 ci 个簇。数学上,ci 的取值满足:
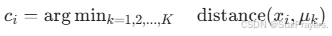
(即选择距离 xi 最近的簇中心对应的 k 作为 ci)。
3. 更新:重新计算每个簇的中心
- 目标:基于当前的簇分配结果,更新每个簇的中心(用簇内所有样本的均值表示)。
- 操作:对第 k 个簇,假设其包含的样本为 {xi∣ci=k}(记为 Sk),
- 则新的簇中心 μk 为:
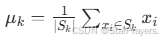
- 其中 ∣Sk∣ 是第 k 个簇的样本数量(若簇为空,可重新随机选择一个样本作为中心)。
4. 收敛判断:重复分配与更新,直到簇中心稳定
- 停止条件:当簇中心 μk 不再显著变化(如变化量小于预设阈值),或迭代次数达到上限时,算法停止。此时的簇分配结果即为最终聚类结果。
②核心数学公式与优化目标
K-means 的本质是最小化簇内平方和(Sum of Squared Errors, SSE),
这是算法的核心优化目标。
1. 距离度量(以欧氏距离为例)
样本 xi 与簇中心 μk 的欧氏距离定义为:
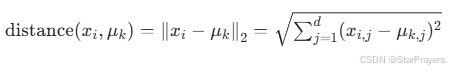
其中 xi,j 是样本 xi 的第 j 个特征,μk,j 是簇中心 μk 的第 j 个特征。
在实际计算中,为了简化运算(避免开平方),通常用平方欧氏距离替代:
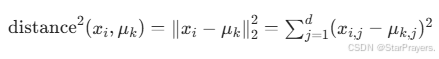
2. 优化目标:最小化簇内平方和(SSE)
K-means 的目标函数是所有样本到其所属簇中心的平方距离之和,即:
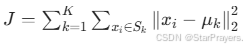
其中 Sk 是第 k 个簇的样本集合。
算法的迭代过程(分配→更新)本质上是对目标函数 J 的优化:
- 分配步骤:固定簇中心 μk,通过给每个样本分配最近的簇,最小化 J(此时 ci 是优化变量)。
- 更新步骤:固定簇分配 ci,通过计算簇内均值更新 μk,进一步最小化 J(此时 μk 是优化变量)。
这种 "固定一部分变量,优化另一部分" 的方法,本质是坐标下降法的一种体现。
三、K-means 聚类实操步骤
①实操核心流程(以 Python sklearn 为例)
1. 数据预处理(关键前提)
- 缺失值处理:用均值、中位数填充或删除缺失样本,避免影响簇中心计算。
- 特征标准化:对数值型特征做标准化(StandardScaler)或归一化(MinMaxScaler),消除量纲差异(如 "年龄" 和 "收入" 单位不同)。
- 特征筛选:剔除冗余、无关特征,减少噪声对聚类结果的干扰。
2. 簇数 K 值确定(避免盲目预设)
- 肘部法则:计算不同 K(通常 2-10)对应的簇内平方和(SSE),绘制 K-SSE 曲线,曲线 "肘部"(SSE 下降速率骤减)对应的 K 即为最优值。
- 轮廓系数法:计算各 K 下的轮廓系数(取值 - 1~1),系数越接近 1,聚类效果越好,选择系数最大的 K。
- 业务经验法:结合实际场景,比如客户分群可根据业务目标预设 K=3(高、中、低价值客户)。
3. 模型训练与优化
- 初始化优化:使用 sklearn 中 KMeans 的
n_init=10(默认值),多次随机初始化簇中心,选择 SSE 最小的结果,避免局部最优。 - 迭代设置:设置
max_iter=300(默认最大迭代次数),确保算法有足够时间收敛。 - 距离度量:默认用欧氏距离,若特征是稀疏数据或需考虑权重,可改用曼哈顿距离(
metric='manhattan')。
4. 结果输出与可视化
- 输出簇标签:通过
model.labels_获取每个样本的簇归属。 - 输出簇中心:通过
model.cluster_centers_获取 K 个簇的中心坐标。 - 可视化:高维数据先用 PCA 降维至 2D/3D,再用散点图绘制不同簇的分布,直观观察聚类效果。
②参数选择细节
| 参数 | 作用 | 推荐设置 |
|---|---|---|
| n_clusters | 指定簇数 K | 结合肘部法则 + 业务场景确定 |
| n_init | 初始簇中心尝试次数 | 10(默认,数据量大时可增至 20) |
| max_iter | 最大迭代次数 | 300(默认,复杂数据可设 500) |
| metric | 距离度量方式 | 欧氏距离(默认)、曼哈顿距离 |
| random_state | 随机种子 | 设固定值(如 42),保证结果可复现 |
③聚类效果评估指标
1. 内部评估(无需真实标签)
- 簇内平方和(SSE):值越小说明簇内越紧凑,但 K 增大时 SSE 会持续下降,需结合肘部法则判断。
- 轮廓系数(Silhouette Coefficient):综合考虑簇内紧凑度和簇间分离度,取值越接近 1 效果越好。
- Calinski-Harabasz 指数:比值越大,说明簇内越紧凑、簇间越分散,聚类效果越优。
2. 外部评估(有真实标签时)
- 调整兰德指数(ARI):衡量聚类结果与真实标签的一致性,取值 - 1~1,越接近 1 越匹配。
- 互信息指数(NMI):量化聚类结果与真实标签的信息重合度,取值 0~1,值越大效果越好。
四、关键特点
- 优点:计算效率高、易于实现,适合处理大规模数据集。
- 缺点:需提前确定 K 值、对初始簇中心敏感(可能陷入局部最优)、对异常值敏感,更适用于凸形分布的数据。
五、典型应用场景
- 客户分群:根据消费行为、用户画像将客户划分为不同群体,支撑精准营销。
- 图像分割:将图像像素按颜色、纹理等特征聚类,实现目标区域提取。
- 数据降维可视化:通过聚类将高维数据映射到低维空间,便于观察数据分布规律。