机器学习入门＜4＞RBFN算法详解

本文用生动的比喻和直观的可视化，带你一步步理解RBFN的核心思想，无需深厚数学背景也能掌握这一经典机器学习算法。

一、引入：从生物大脑到人工神经网络

1. 脑科学启示录：智慧的"社交网络"

你知道吗？ 人脑拥有约860亿个神经元，它们相互连接形成一个极其复杂的网络。每个神经元都像一个有个性的朋友：

有些朋友活跃范围广（接收很多信息）

有些朋友只在特定话题上活跃（局部响应）

一个生动的比喻：

当有人说火锅时，四川籍的同学反应最强烈；

当有人说冰雪大世界时，东北同学会异常兴奋。

这就是局部响应的特性------不同的神经元对不同的刺激有着不同的敏感度。

连接到RBFN： 今天我们要学习的RBFN（径向基函数网络），正是模拟这种特定领域专家的神经网络！

2. 与之前知识的对比：从"全能选手"到"专业专家"

如果不了解逻辑回归，可以阅读我之前写的博客：https://blog.csdn.net/2303_77568009/article/details/155580110?spm=1001.2014.3001.5501

让我们先回顾一下之前学过的逻辑回归：

逻辑回归像一个全能型选手，对所有特征一视同仁
它试图找到一个全局的决策边界

但现实世界往往更加复杂：

体温37.5°C 是发烧，但气温37.5°C是凉爽。

Apple在科技话题中指苹果公司，在水果店就是苹果。

我们需要一种能理解上下文和范围的智能模型------这就是RBFN！

二、核心概念："局部专家"系统

1. RBFN的三层结构比喻：公司决策系统

想象一个公司的决策流程：

复制代码

  输入层   →  隐藏层  → 输出层
    ↓         ↓         ↓
信息收集员 → 部门专家 → CEO决策

具体来说：

输入层：市场信息收集员（收集原始数据）
隐藏层：各部门专家（财务部、技术部、市场部...）
输出层：CEO（综合专家意见做最终决策）

2. 核心：径向基函数------专家的"专业领域"

径向基函数就像每个专家的能力范围：

中心点：专家的舒适区
- 比如财务专家最擅长处理成本在100-200万的项目
半径（σ）：专家的知识范围
- σ小 = 专精窄领域
- σ大 = 知识面广但不深
响应值：数据离专家中心越近，专家的发言权越大

三、工作原理："专家会诊"流程

1. 完整流程故事化：医疗诊断系统

假设我们要构建一个医疗诊断系统，判断患者是否患有某种疾病。

步骤1：数据收集（输入层）

步骤2：专家诊断（隐藏层）

步骤3：加权决策（输出层）

2. 关键特性总结

局部性：每个神经元只关心自己"辖区"内的事情
可解释性：可以查看哪个"专家"贡献最大------比黑箱网络更透明
插值能力：即使遇到没见过的情况，也能参考最近似专家的意见

四、对比与可视化：RBFN vs 其他网络

1. 直观对比演示

场景：二维平面上分类同心圆数据

下面我将使用Python实现逻辑回归和RBF神经网络(RBFN)对同心圆数据进行分类，并直观展示它们的不同表现。

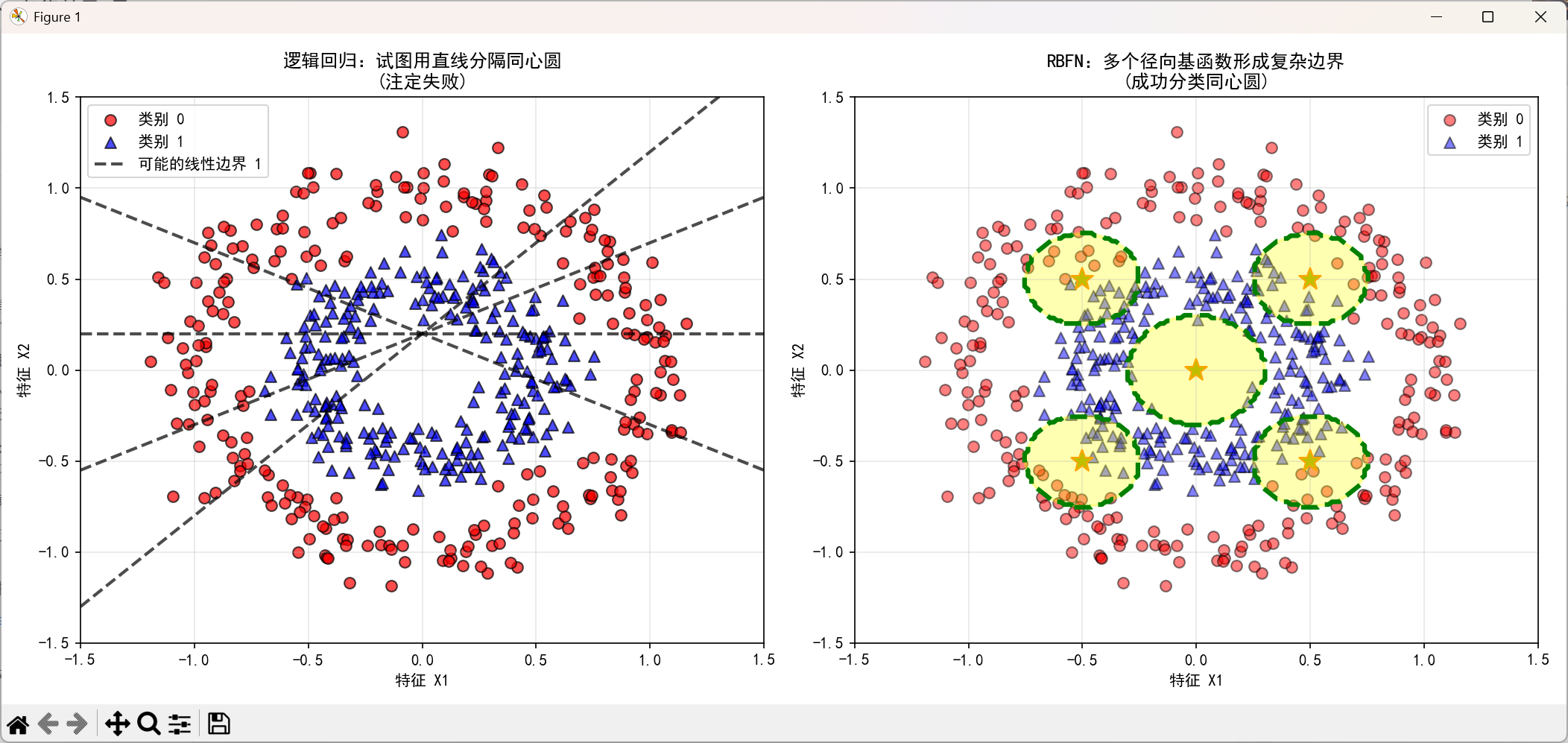
逻辑回归：试图画一条直线分开------失败！
RBFN：放置多个感应圈------成功分类！

关键洞察：RBFN通过多个局部区域组合，可以形成复杂的非线性边界。

2. 应用场景展示

人脸识别：每个RBF神经元关注面部特定区域
- 眼睛区域专家
- 鼻子区域专家
- 嘴巴区域专家
股票预测：不同专家关注不同市场状态
- 暴涨模式专家
- 暴跌模式专家
- 震荡市场专家
语音识别：专家们各自擅长识别不同的音素或音节

五、动手体验：不用数学的理解

1. 互动游戏：你是RBFN！

游戏规则：

将教室（或想象的空间）划分成6个区域
每个区域有一个"专家"，每个专家有自己的"专业领域"
展示物品描述，各"专家"根据接近程度打分（0-10）
"CEO"综合所有专家意见做出最终判断

示例：

物品："一个红色的金属圆形徽章"

红色物体专家：9分
金属物体专家：8分
圆形物体专家：10分
其他专家：低分或0分

在这里为了大家能够理解，我用python将上面的内容可视化了（代码在文章的末尾获取）：

2. 极简代码，开箱即用

python 复制代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.linear_model import LinearRegression
import warnings

warnings.filterwarnings('ignore')  # 忽略警告信息

# 设置中文字体，解决中文乱码问题
plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'DejaVu Sans']  # 设置中文字体
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题


class SimpleRBFN:
    """简化的RBF网络实现（教学用）"""

    def __init__(self, n_centers=20, sigma=0.5):
        self.n_centers = n_centers
        self.sigma = sigma
        self.centers = None
        self.linear_model = LinearRegression()

    def _rbf_kernel(self, X, center):
        """径向基函数（高斯核）"""
        return np.exp(-np.sum((X - center) ** 2, axis=1) / (2 * self.sigma ** 2))

    def fit(self, X, y):
        # 1. 使用KMeans确定中心点
        kmeans = KMeans(n_clusters=self.n_centers, random_state=42)
        kmeans.fit(X)
        self.centers = kmeans.cluster_centers_

        # 2. 计算RBF特征
        rbf_features = np.zeros((len(X), self.n_centers))
        for i, center in enumerate(self.centers):
            rbf_features[:, i] = self._rbf_kernel(X, center)

        # 3. 训练线性回归层
        self.linear_model.fit(rbf_features, y)
        return self

    def predict(self, X):
        # 计算RBF特征
        rbf_features = np.zeros((len(X), self.n_centers))
        for i, center in enumerate(self.centers):
            rbf_features[:, i] = self._rbf_kernel(X, center)

        # 线性回归预测
        return self.linear_model.predict(rbf_features)


# 使用示例
np.random.seed(42)  # 设置随机种子，确保结果可重复
X = np.linspace(0, 10, 100).reshape(-1, 1)
y = np.sin(X).ravel() + np.random.normal(0, 0.1, 100)

# 创建并训练RBF网络
rbfn = SimpleRBFN(n_centers=20, sigma=0.5)
rbfn.fit(X, y)

# 预测
X_test = np.linspace(0, 10, 200).reshape(-1, 1)
y_pred = rbfn.predict(X_test)

# 可视化
plt.figure(figsize=(12, 8))

# 绘制原始数据和预测结果
plt.scatter(X, y, alpha=0.5, label='原始数据（带噪声）', s=30)
plt.plot(X_test, y_pred, 'r-', linewidth=3, label='RBFN预测结果')

# 添加网格线
plt.grid(True, linestyle='--', alpha=0.6)

# 添加图例和标题
plt.legend(fontsize=12)
plt.title('RBFN神经网络：从噪声数据中学习正弦函数', fontsize=16, fontweight='bold')
plt.xlabel('X轴', fontsize=12)
plt.ylabel('Y轴', fontsize=12)

# 添加注释说明
plt.text(0.5, 1.1, 'RBFN参数：20个中心点，σ=0.5',
         transform=plt.gca().transAxes,
         fontsize=11,
         verticalalignment='top',
         bbox=dict(boxstyle='round', facecolor='wheat', alpha=0.5))

plt.tight_layout()
plt.show()

这段代码实现了一个简化版径向基函数网络（RBFN），用于从带噪声的数据中学习正弦函数的模式。整个实现分为三部分：网络结构定义、训练过程和可视化展示。

首先，代码定义了一个SimpleRBFN类，它采用三层结构设计：输入层接收数据，隐含层使用高斯径向基函数进行非线性变换，输出层通过线性回归完成最终预测。网络的中心点通过K-means聚类确定，高斯函数的宽度由sigma参数控制，这种结构使网络能够有效捕捉数据的局部特征和全局趋势。

其次，训练过程遵循三个关键步骤：使用K-means算法自动确定径向基函数的中心点位置；计算每个样本点到所有中心点的高斯核函数值，形成新的特征表示；最后用线性回归模型学习这些特征到目标值的映射关系。代码中使用了带噪声的正弦波数据作为示例，展示了网络对复杂非线性关系的拟合能力。

最后，代码通过可视化直观展示学习效果：原始数据点以散点图显示，RBFN的预测结果以平滑曲线叠加，清晰对比了噪声数据与网络恢复的函数形态。图中还标注了网络参数信息，完整呈现了从数据预处理、模型训练到结果评估的全过程，体现了RBFN在处理非线性回归问题上的实用性和有效性。

总而言之，这个代码做了一个有趣的事情：它用一个小型神经网络从一堆有干扰的数据点中，找出背后隐藏的真实规律。

具体来说，先生成了一组加了随机干扰的正弦波数据点，看起来比较杂乱；然后让一个RBF神经网络去学习这些数据，这个网络会先找出20个代表性的中心点，然后根据这些中心点来计算每个数据的位置特征；最后网络会找出这些特征与原始数据之间的关系，形成一个平滑的预测曲线。最终画图展示时，可以看到虽然原始数据点很分散，但神经网络还是成功还原出了清晰的正弦波形状。

参数调整实验：

调整 n_centers（专家数量）
- 太少 → 欠拟合（专家不够用）
- 太多 → 过拟合（专家太多，各自为政）
调整 width（专家知识范围）
- 太窄 → 过于敏感（专家太专）
- 太宽 → 过于模糊（专家知识面太广）

六、总结升华：RBFN的哲学

1. 核心思想总结

RBFN的精髓可以概括为三点：

分而治之：复杂问题分解为多个简单子问题
专业分工：每个神经元成为特定领域的专家
民主集中：局部意见通过加权形成全局决策

2. 与生物神经网络的联系

RBFN更接近真实大脑的工作方式
大脑皮层中的"柱状结构"就是局部处理单元
深度学习的卷积神经网络（CNN）也受此启发------局部感受野！

七、本文中绘图的代码

1.Python实现逻辑回归和RBF神经网络(RBFN)对同心圆数据进行分类，并直观展示它们的不同表现。

python 复制代码

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.datasets import make_circles
from sklearn.linear_model import LogisticRegression
from sklearn.neural_network import MLPClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False

# 生成同心圆数据
np.random.seed(42)
X, y = make_circles(n_samples=500, factor=0.5, noise=0.1, random_state=42)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 创建两个模型
# 1. 逻辑回归（线性分类器）
logistic_model = make_pipeline(StandardScaler(), LogisticRegression(max_iter=1000, random_state=42))

# 2. RBF神经网络（使用MLPClassifier模拟RBFN，设置合适的隐藏层和激活函数）
# 注意：这里使用MLPClassifier的tanh激活函数来模拟RBFN的效果
rbfn_model = make_pipeline(
    StandardScaler(),
    MLPClassifier(
        hidden_layer_sizes=(50,),  # 一个包含50个神经元的隐藏层
        activation='tanh',         # 使用tanh激活函数模拟径向基函数
        solver='lbfgs',
        max_iter=1000,
        random_state=42,
        alpha=0.01
    )
)

# 训练模型
logistic_model.fit(X_train, y_train)
rbfn_model.fit(X_train, y_train)

# 评估模型
logistic_train_acc = accuracy_score(y_train, logistic_model.predict(X_train))
logistic_test_acc = accuracy_score(y_test, logistic_model.predict(X_test))

rbfn_train_acc = accuracy_score(y_train, rbfn_model.predict(X_train))
rbfn_test_acc = accuracy_score(y_test, rbfn_model.predict(X_test))

# 创建可视化网格
h = 0.02  # 网格步长
x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                     np.arange(y_min, y_max, h))

# 为每个模型计算决策边界
fig, axes = plt.subplots(1, 3, figsize=(18, 5))

# 自定义颜色映射
cmap_light = ListedColormap(['#FFAAAA', '#AAAAFF'])
cmap_bold = ListedColormap(['#FF0000', '#0000FF'])

# 1. 原始数据
ax = axes[0]
ax.scatter(X_train[y_train == 0, 0], X_train[y_train == 0, 1], 
           c='red', marker='o', edgecolors='k', s=40, label='类别 0', alpha=0.7)
ax.scatter(X_train[y_train == 1, 0], X_train[y_train == 1, 1], 
           c='blue', marker='^', edgecolors='k', s=40, label='类别 1', alpha=0.7)
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_title('原始数据分布\n(同心圆)')
ax.set_xlabel('特征 X1')
ax.set_ylabel('特征 X2')
ax.legend()
ax.grid(True, alpha=0.3)

# 2. 逻辑回归决策边界
ax = axes[1]
Z_logistic = logistic_model.predict(np.c_[xx.ravel(), yy.ravel()])
Z_logistic = Z_logistic.reshape(xx.shape)

# 绘制决策区域
ax.contourf(xx, yy, Z_logistic, cmap=cmap_light, alpha=0.8)

# 绘制训练数据点
ax.scatter(X_train[y_train == 0, 0], X_train[y_train == 0, 1], 
           c='red', marker='o', edgecolors='k', s=40, label='类别 0')
ax.scatter(X_train[y_train == 1, 0], X_train[y_train == 1, 1], 
           c='blue', marker='^', edgecolors='k', s=40, label='类别 1')

# 尝试绘制逻辑回归的"直线"决策边界
# 获取逻辑回归的系数
if hasattr(logistic_model.named_steps['logisticregression'], 'coef_'):
    coef = logistic_model.named_steps['logisticregression'].coef_[0]
    intercept = logistic_model.named_steps['logisticregression'].intercept_[0]
    
    # 绘制决策直线
    x_plot = np.array([xx.min(), xx.max()])
    y_plot = -(coef[0] * x_plot + intercept) / coef[1]
    ax.plot(x_plot, y_plot, 'k--', linewidth=3, label='逻辑回归决策边界')

ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_title(f'逻辑回归 (线性分类器)\n训练集准确率: {logistic_train_acc:.2%}, 测试集准确率: {logistic_test_acc:.2%}')
ax.set_xlabel('特征 X1')
ax.set_ylabel('特征 X2')
ax.legend(loc='upper right')
ax.grid(True, alpha=0.3)

# 3. RBFN决策边界
ax = axes[2]
Z_rbfn = rbfn_model.predict(np.c_[xx.ravel(), yy.ravel()])
Z_rbfn = Z_rbfn.reshape(xx.shape)

# 绘制决策区域
ax.contourf(xx, yy, Z_rbfn, cmap=cmap_light, alpha=0.8)

# 绘制训练数据点
ax.scatter(X_train[y_train == 0, 0], X_train[y_train == 0, 1], 
           c='red', marker='o', edgecolors='k', s=40, label='类别 0')
ax.scatter(X_train[y_train == 1, 0], X_train[y_train == 1, 1], 
           c='blue', marker='^', edgecolors='k', s=40, label='类别 1')

# 为了直观展示RBFN的"感应圈"，我们在图中标记一些"径向基函数中心"
# 这里随机选取一些训练样本点作为示意
np.random.seed(42)
n_centers = 15
center_indices = np.random.choice(len(X_train), n_centers, replace=False)
centers = X_train[center_indices]

# 绘制径向基函数中心
ax.scatter(centers[:, 0], centers[:, 1], s=150, c='yellow', 
           marker='*', edgecolors='k', linewidth=1.5, alpha=0.8, 
           label=f'RBF中心 (示意, {n_centers}个)')

ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_title(f'RBF神经网络 (非线性分类器)\n训练集准确率: {rbfn_train_acc:.2%}, 测试集准确率: {rbfn_test_acc:.2%}')
ax.set_xlabel('特征 X1')
ax.set_ylabel('特征 X2')
ax.legend(loc='upper right')
ax.grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

# 补充说明图：展示逻辑回归的线性决策边界如何尝试拟合非线性数据
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))

# 左图：逻辑回归试图用一条直线分隔同心圆
ax1.scatter(X[y == 0, 0], X[y == 0, 1], c='red', marker='o', 
            edgecolors='k', s=50, alpha=0.7, label='类别 0')
ax1.scatter(X[y == 1, 0], X[y == 1, 1], c='blue', marker='^', 
            edgecolors='k', s=50, alpha=0.7, label='类别 1')

# 绘制多条可能的"直线"决策边界
x_plot = np.array([-1.5, 1.5])
for i, angle in enumerate([-0.5, 0, 0.5, 1.0]):
    y_plot = angle * x_plot + 0.2
    ax1.plot(x_plot, y_plot, 'k--', linewidth=2, alpha=0.7, 
             label=f'可能的线性边界 {i+1}' if i == 0 else None)

ax1.set_xlim(-1.5, 1.5)
ax1.set_ylim(-1.5, 1.5)
ax1.set_title('逻辑回归：试图用直线分隔同心圆\n(注定失败)')
ax1.set_xlabel('特征 X1')
ax1.set_ylabel('特征 X2')
ax1.legend()
ax1.grid(True, alpha=0.3)

# 右图：RBFN使用多个径向基函数形成复杂决策边界
ax2.scatter(X[y == 0, 0], X[y == 0, 1], c='red', marker='o', 
            edgecolors='k', s=50, alpha=0.5, label='类别 0')
ax2.scatter(X[y == 1, 0], X[y == 1, 1], c='blue', marker='^', 
            edgecolors='k', s=50, alpha=0.5, label='类别 1')

# 绘制几个径向基函数（感应圈）的示意图
centers = np.array([[0, 0], [0.5, 0.5], [-0.5, -0.5], [0.5, -0.5], [-0.5, 0.5]])
radii = [0.3, 0.25, 0.25, 0.25, 0.25]

for center, radius in zip(centers, radii):
    circle = plt.Circle(center, radius, color='yellow', alpha=0.3, linewidth=2, 
                        fill=True, edgecolor='orange')
    ax2.add_patch(circle)
    ax2.plot(center[0], center[1], 'y*', markersize=15, markeredgecolor='orange')

# 绘制RBFN形成的复杂决策边界
xx, yy = np.meshgrid(np.linspace(-1.5, 1.5, 200),
                     np.linspace(-1.5, 1.5, 200))
grid_points = np.c_[xx.ravel(), yy.ravel()]

# 模拟一个简单的RBF决策函数
def simple_rbf_decision(points, centers, radii):
    decisions = []
    for point in points:
        # 简单模拟：如果点在某个中心的内圈，则分类为1，否则为0
        class_1 = False
        for center, radius in zip(centers, radii):
            distance = np.sqrt((point[0]-center[0])**2 + (point[1]-center[1])**2)
            if distance < radius:
                class_1 = True
                break
        decisions.append(1 if class_1 else 0)
    return np.array(decisions)

Z_simple_rbf = simple_rbf_decision(grid_points, centers, radii)
Z_simple_rbf = Z_simple_rbf.reshape(xx.shape)

# 绘制决策边界
ax2.contour(xx, yy, Z_simple_rbf, levels=[0.5], colors='green', linewidths=3, linestyles='--')

ax2.set_xlim(-1.5, 1.5)
ax2.set_ylim(-1.5, 1.5)
ax2.set_title('RBFN：多个径向基函数形成复杂边界\n(成功分类同心圆)')
ax2.set_xlabel('特征 X1')
ax2.set_ylabel('特征 X2')
ax2.legend()
ax2.grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

# 打印模型性能对比
print("="*60)
print("模型性能对比")
print("="*60)
print(f"逻辑回归:")
print(f"  训练集准确率: {logistic_train_acc:.2%}")
print(f"  测试集准确率: {logistic_test_acc:.2%}")
print(f"  线性决策边界，无法处理复杂非线性模式")
print()
print(f"RBF神经网络:")
print(f"  训练集准确率: {rbfn_train_acc:.2%}")
print(f"  测试集准确率: {rbfn_test_acc:.2%}")
print(f"  非线性决策边界，通过径向基函数成功捕捉复杂模式")
print("="*60)

2.互动游戏：你是RBFN！

python 复制代码

import matplotlib.pyplot as plt

# 修复中文显示问题
plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial']  # 使用黑体或Arial
plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题

# 定义专家和评分
experts = ['红色专家', '金属专家', '圆形专家', '其他1', '其他2', '其他3']
scores = [9, 8, 10, 2, 1, 0]
colors = ['red', 'silver', 'blue', 'gray', 'gray', 'gray']

# 创建图表
fig, ax = plt.subplots(figsize=(10, 6))

# 绘制专家评分
for i, (expert, score, color) in enumerate(zip(experts, scores, colors)):
    ax.scatter(i, 5, s=score*100, alpha=0.6, c=color, edgecolors='black')
    ax.text(i, 5, f'{score}', ha='center', va='center', fontsize=12, fontweight='bold')
    ax.text(i, 8, expert, ha='center', fontsize=10)

# 添加CEO判断
ax.text(2.5, 1, 'CEO综合判断: 红色金属圆形物品', 
        ha='center', fontsize=14, fontweight='bold',
        bbox=dict(boxstyle='round,pad=0.5', facecolor='gold', alpha=0.8))

# 设置图表
ax.set_title('RBFN游戏: "一个红色的金属圆形徽章"', fontsize=16, fontweight='bold')
ax.set_xlim(-1, 6)
ax.set_ylim(0, 10)
ax.axis('off')  # 隐藏坐标轴
plt.tight_layout()
plt.show()

这段代码做了三件事：

用不同颜色和大小的圆圈表示6个专家的评分（圆圈越大分数越高）
用文字标出每个专家的分数
在底部显示CEO的综合判断结果