本文是记录专业课计算机图形学的部分笔记,参考教材为Angel的第八版交互式计算机图形学------基于WebGL 2.0的自顶向下方法。
1、对于上讲的GH和IJ无法区分的问题,我们考虑线段的参数化表示:p(α) = (1-α)p1+ αp2,其中1≥α≥0。参数表示的优点有普适性、几何意义明确、参数取值范围明确。在计算出来线段所在直线与窗口各边交点对应的α值后,我们可以通过这些参数值的顺序区分出各种情形:

按照参数方向,进行比较,是否重叠:
①考察2个起始边交点的最大值,参数表示
②考察2个终止边交点的最小值,参数表示

优势是和Cohen-Sutherland 算法一样很简单地接受或拒绝,并且应用α值使得不必要像Cohen-Sutherland算法那样反复应用代码,最多4次除法。
2、补充Angel教材没讲清楚的地方:
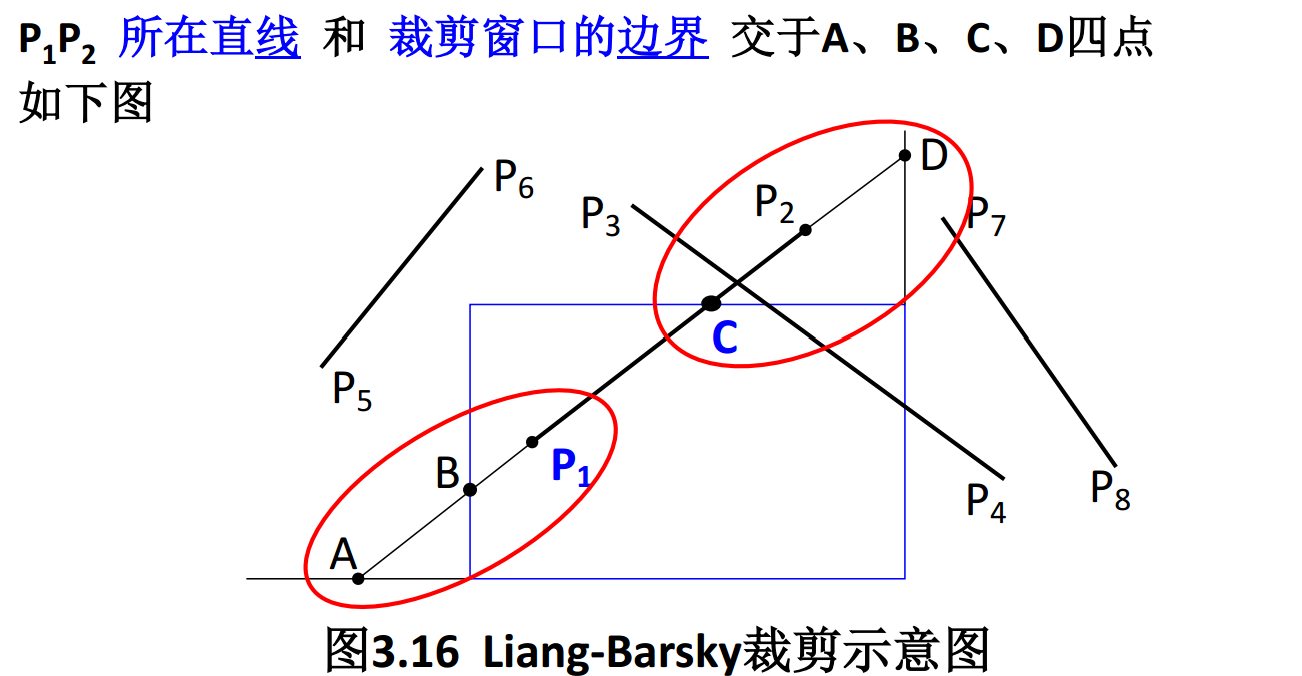
算法的基本思想其实是从A、B和P1三点中找出最靠近P2的点(图中这里为 P1点)、从C、D和P2三点中找出最靠近P1的点(图中这里为 C 点)。那么,P1C 就是P1P2线段上的可见部分。

如果点(x,y)满足:XWmin≤x≤XWmax、YWmin≤y≤YWmax,那么这个点在窗口内。下面,按参数化形式写出该式的裁剪条件:

这四个不等式的含义显然还是大于左边、小于右边、大于下边、小于上边。

pk非零时,不等式就可以变成u≤qk/pk或u≥qk/pk。如果把每条窗边看成有一个指向外侧的单位法向量nk(比如左边的外法线指向左:(−1,0)),那么可以把pk写成点积:pk=nk⋅d,也就是说pk告诉了你线段方向d在相对于该边外法线上的投影。
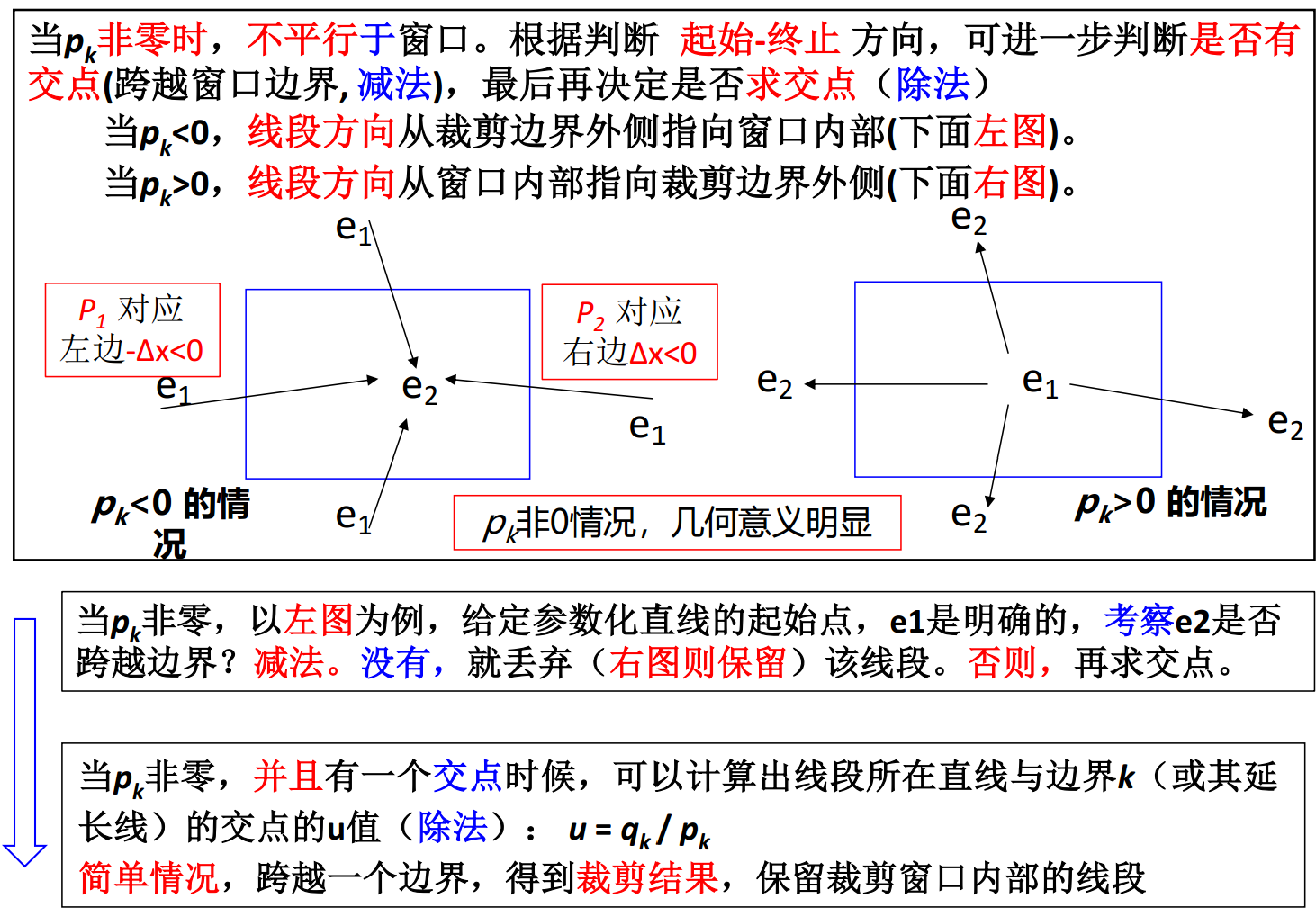
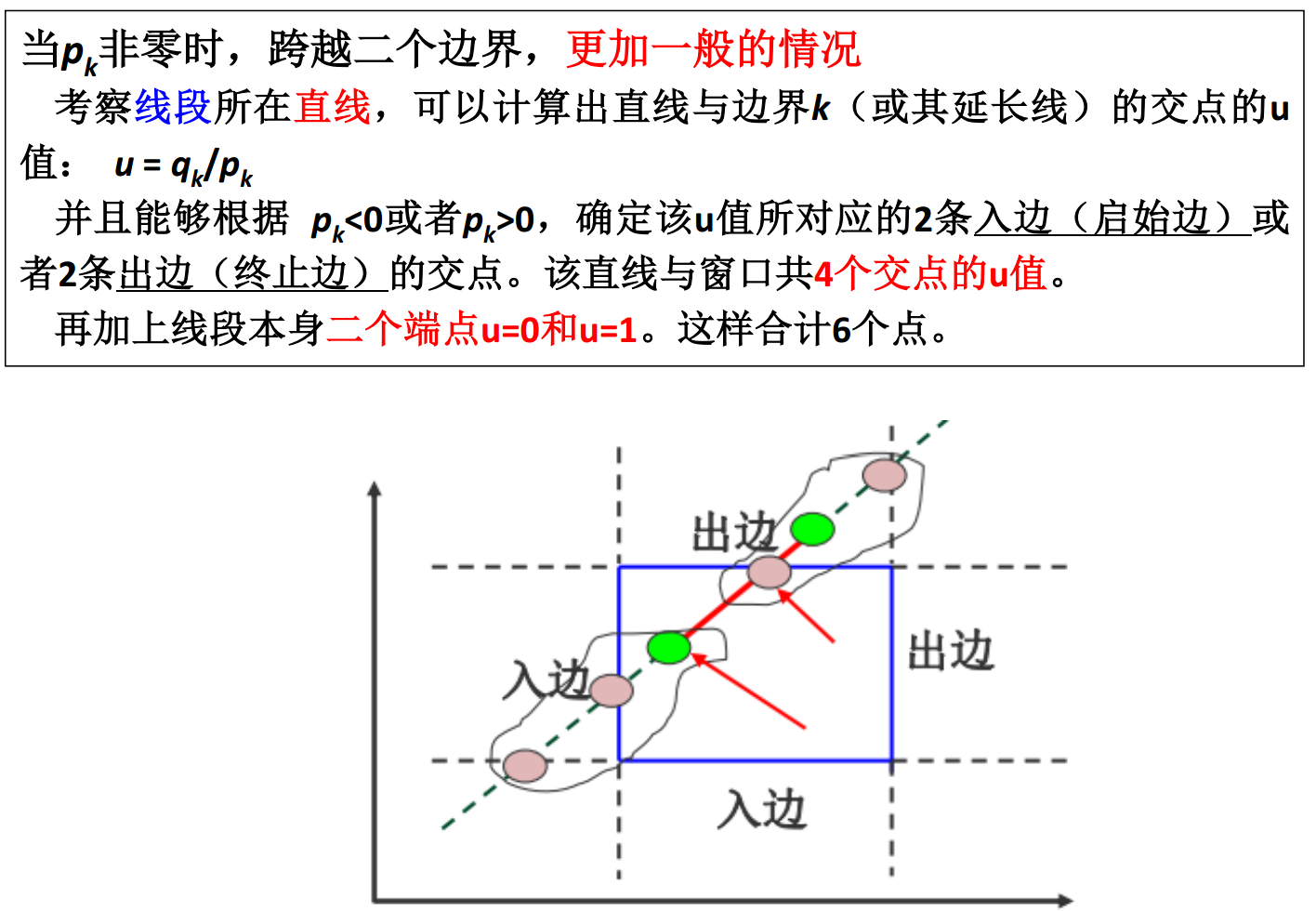
u=qk/pk的这个u就是线与该边相交的参数位置(如果交点在参数区间内的话就是实际的交点),如果pk<0(进入边),则u给出一个下界,反之则给出一个上界。


3、Cohen-Sutherland 算法和梁友栋-Barsky算法,这二种算法也可以推广到三维的情形。相比之下,一些其他高效的二维算法不能扩展到三维情形。
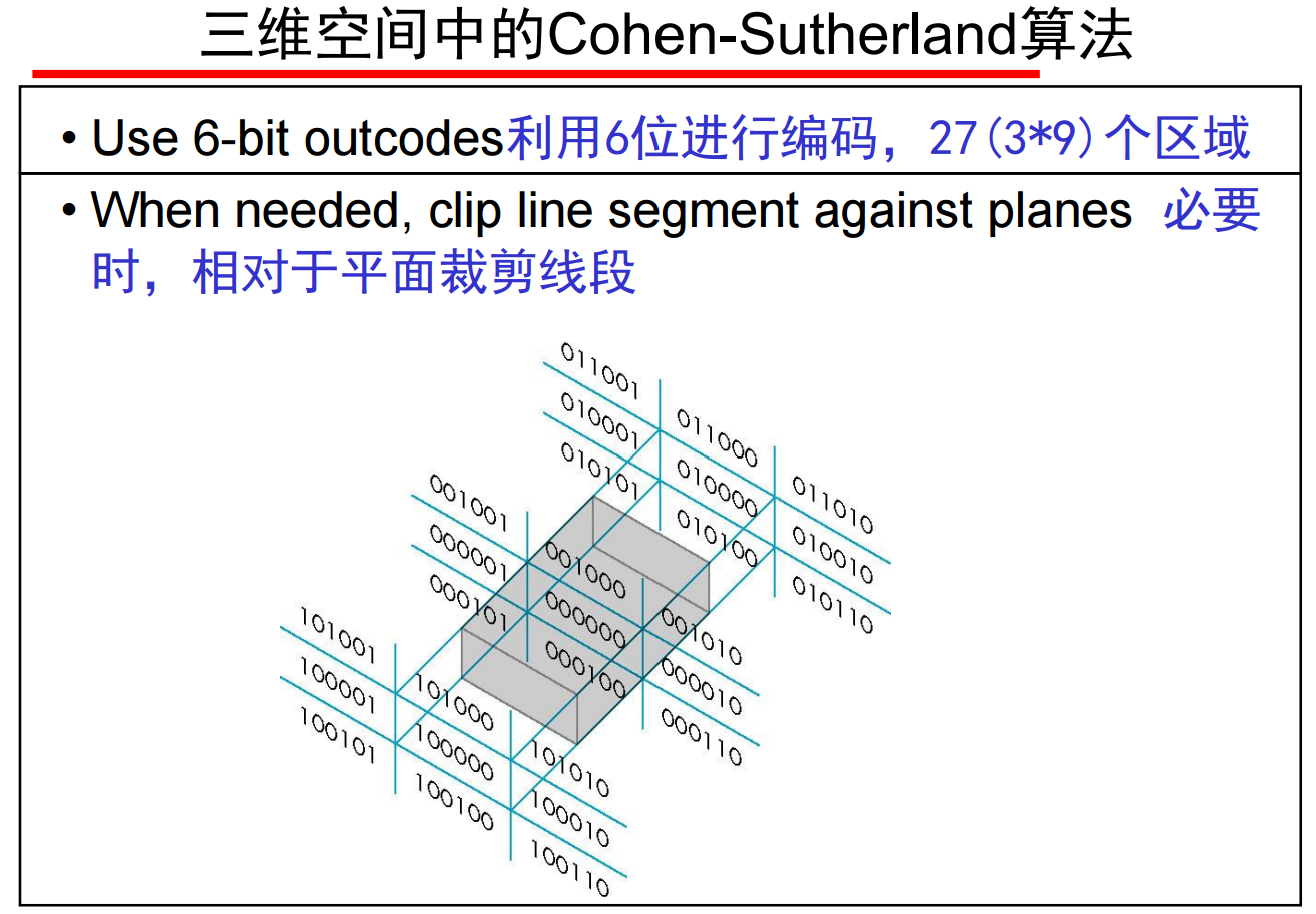
在三维空间中一般的裁剪需要计算线段与任意平面的交点,其中,求交需要6次乘法运算和1次浮点除法运算。

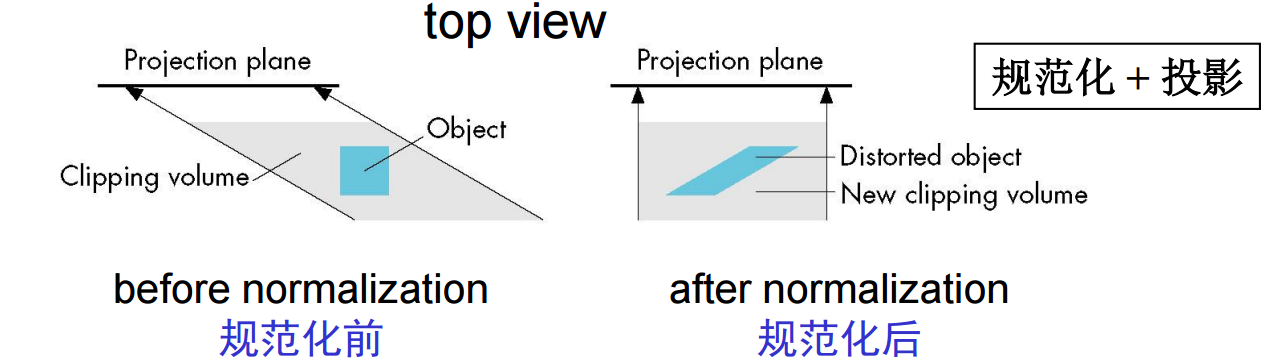
规范化过程是视图生成的一部分(在裁剪前进行)。在规范化后,我们相对于正平行六面体(立方体)进行裁剪,这时典型的求交计算只需要一次浮点减法,例如:是否x -- xmax > 0?