算法实现 - C/C++
前言
总结积累平时研究的算法,不定时更新,便于形成体系。
积累习惯:
- 一张图形象描述问题
- 该算法触动/记忆点
- 算法策略(分递二,回贪动)
- 算法代码含关键理解点
1. 数据结构类
2. 常见算法类
2.1 n皇后
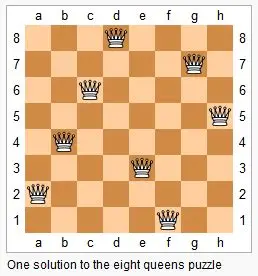
25年下半年软考算法题。
当时脑子里只有queen[i][j]的二维解法,案例使用k表行,queen[k]表列时有点懵(没这个概念)。虽然跌跌撞撞写出了大部分,但主要是题目引导和举实例试出来的。
策略:回溯法
法一: 案例解法
c
#include<stdio.h>
#include<math.h>
#define N 100 // 最多摆放100个皇后
int n,queen[N]; // 关键理解:queen[k] 表示 "第 k 行的皇后放在第queen[k]列"(行和列均从 0 开始计数)。
// 例如:queen[0] = 1 表示第 0 行的皇后在第 1 列。
// 这种设计天然避免了 "同一行多个皇后" 的冲突(因为每行只存一个列号)。
int num = 0; // 总共有多少方案
void Putqueen(int k) // 假设前k个皇后已经摆好,现在摆放第K个皇后
{
int i,j;
if(k==n) // 终止条件:第 0 到第 n-1 行的皇后都已摆放完成(共 n 行,即所有皇后都放好了)。
{
for(i=0;i<n;i++)
{
printf("(%d,%d)\t",i+1,queen[i]+1); // 输出时 i+1 和 queen[i]+1 是将 "0 开始的索引" 转换为 "1 开始的棋盘坐标"(符合日常习惯)。
}
printf("\n");
num ++;
}
else
{
for(i=0;i<n;++i) // 尝试将第k行皇后放在第i列 (同一行一例一列试)
{
for(j=0;j<k;++j) // 检查当前位置(i列)与前k行皇后是否冲突
{
if(i==queen[j]||abs(queen[j]-i)==abs(j-k)) // 冲突条件:同列 或 同对角线
{
break; //有冲突,跳出检查,尝试下一列
}
}
if(j==k) // 前k行都无冲突(当前列i合法)
{
queen[k]=i; // 记录第k行皇后在第i列
Putqueen(k+1); // 递归摆放下一行(第k+1行)
}
}
}
}
int main()
{
scanf("%d",&n); // 输入皇后数量n
Putqueen(0); // 从第0行开始摆放皇后
printf("num: %d\n\n", num); // 输出方案数量
return 0;
}法二:法一上优化冲突检查方式
空间换时间,尤其适合求解较大 n 的问题.
c
#include<stdio.h>
#include<math.h>
#define N 100 //最多摆放100个皇后
int n;
int queen[N];
int visited[3][2*N-2]; // visited数组:记录列、主对角线、副对角线是否被占用
// 其中:
// visited[0][i]:标记第i列是否有皇后(列冲突)
// visited[1][k+i]:标记主对角线(k+i为定值)是否有皇后(主对角线冲突)
// visited[2][k-i+n]:标记副对角线(k-i为定值,加n避免负数索引)是否有皇后(副对角线冲突)
/*
核心思路:用visited数组提前记录 "已被皇后占用的列和对角线",每次检查冲突时无需遍历前 k 行,直接通过 3 个索引判断:
列冲突:第 i 列是否被占用(visited[0][i]);
主对角线冲突:对于第 k 行第 i 列,主对角线的特征是 "行 + 列 = k+i"(同一主对角线上的所有位置,行 + 列的值相同),因此用visited[1][k+i]标记;
副对角线冲突:对于第 k 行第 i 列,副对角线的特征是 "行 - 列 = k-i"(同一副对角线上的所有位置,行 - 列的值相同),但k-i可能为负数,因此加 n(偏移量)避免数组索引为负,用visited[2][k-i+n]标记。
操作:摆放皇后时,将对应的列、主对角线、副对角线标记为 "占用"(置 1);回溯时(递归返回后),再重置为 "未占用"(置 0),确保不影响其他分支的尝试。
*/
void Putqueen(int k)
{
int i,j;
if(k==n) //递归出口
{
for(i=0;i<n;i++)
printf("(%d,%d)\t",i+1,queen[i]);
printf("\n");
}
else
{
for(i=0;i<n;i++) // 检查第k行第i列是否与前k行皇后冲突
{
if(!visited[0][i]&&!visited[1][k+i]&&!visited[2][k-i+n]) //k-i可能为负,所以加n
{
queen[k]=i;
visited[0][i]=visited[1][k+i]=visited[2][k-i+n]=1;
Putqueen(k+1);
visited[0][i]=visited[1][k+i]=visited[2][k-i+n]=0;
}
}
}
}
int main()
{
scanf("%d",&n);
Putqueen(0);
return 0;
}
/*
1. 时间效率显著提升:通过 "空间换时间",将冲突检查从 O (k) 优化为 O (1),总时间复杂度从O(n! * n²)降至O(n!),尤其在 n 较大时(如 n=12 以上),运行速度会明显更快。
2. 空间开销可控:虽然增加了visited数组,但空间复杂度仍为 O (n),没有本质增加,属于 "用少量空间换大幅时间优化" 的典型做法。
*/