图论专题(四)：DFS的“回溯”之舞——探寻「所有可能路径」

哈喽各位，我是前端小L。

欢迎来到我们的图论专题第四篇！在之前的探索中，我们的 DFS/BFS 就像一个"侦察兵"，它的任务是报告"能/不能"到达。但今天，我们要给它一个新任务：扮演一个"探险家 "，不仅要找到宝藏（终点），还要把他走过的每一条 通往宝藏的地图都绘制下来。

这，就是回溯的精髓。它是一种"走一步，看一步，走不通，退一步"的系统性搜索策略，而 DFS 的递归特性，是实现回溯的天然载体。

力扣 797. 所有可能路径

https://leetcode.cn/problems/all-paths-from-source-to-target/

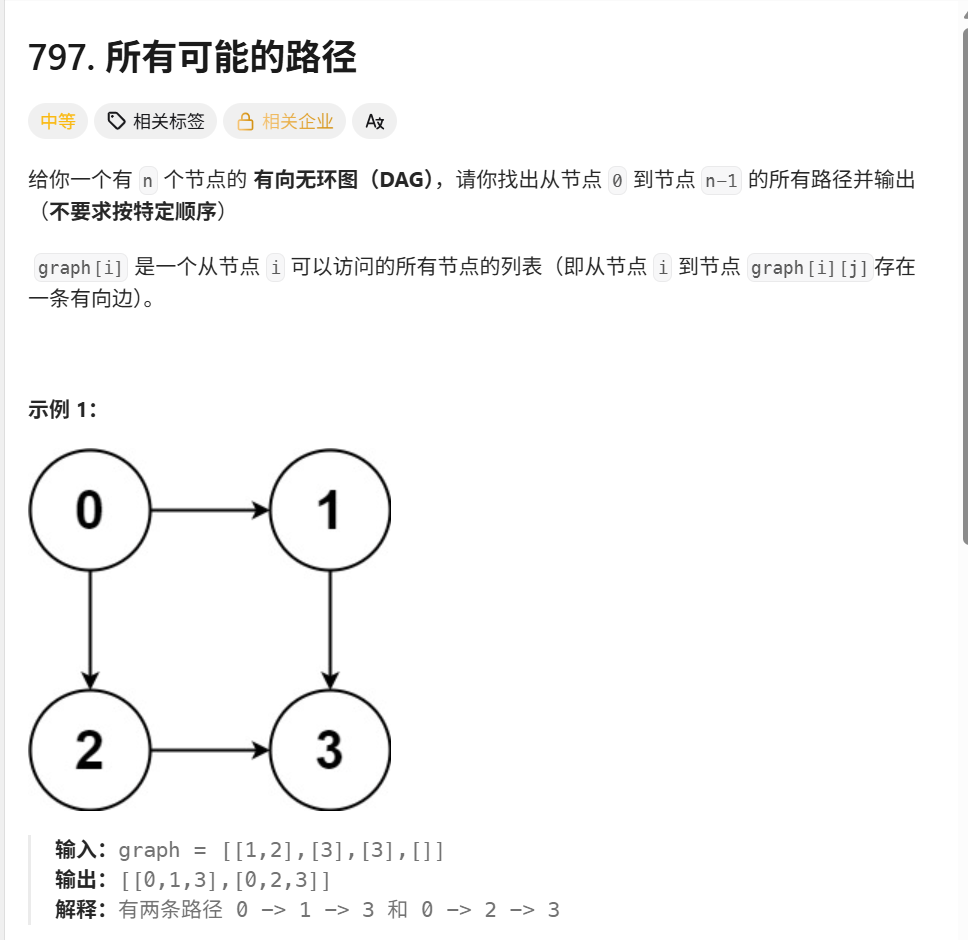
题目分析：

输入：一个有向无环图 (DAG) graph。
"Aha!"时刻 ：输入直接就是邻接表 ！graph[i] 是一个列表，包含 i 能到达的所有节点。我们又一次**省去了"建图"**的步骤！
"Aha!"时刻 2 ：这是一个 DAG （有向无环图）。这意味着我们从 0 出发，永远不会"兜圈"回到 0 。因此，我们不需要 visited 数组来防止无限循环！
目标：找到所有从 0 到 n-1 的路径。

解决方案：DFS + 回溯

既然要"一条路走到黑"地探索所有可能，DFS 是我们的不二之选。我们需要一个"记事本"（currentPath 向量），来记录我们当前走过的足迹。

算法流程：

"探险家"函数 dfs(u)：
- u 是我们当前所在的节点。
- dfs(u) 的职责是：从 u 出发，帮我找到所有能到达 target (即 n-1) 的路径。
全局变量：
- vector<vector<int>> allPaths：存储所有找到的完整路径。
- vector<int> currentPath：存储当前正在探索的路径。
主函数：
- target = n - 1。
- currentPath.push_back(0)（把起点 0 放入"记事本"）。
- 调用 dfs(0)。
- 返回 allPaths。
dfs(u) 的详细逻辑：
- (检查是否到达终点) : if (u == target)
  - 成功！ currentPath 里存的就是一条完整路径。
  - allPaths.push_back(currentPath) (把它存入最终答案)。
  - return (这条路探索完毕)。
- (探索邻居) : for (int v : graph[u])
  - "做选择" (前进)：
    - currentPath.push_back(v) (把邻居 v 加入"记事本")。
    - 递归：dfs(v) (让探险家继续从 v 出发，深入探索)。
  - "撤销选择" (回溯)：
    - currentPath.pop_back()
    - (这是回溯的灵魂！) dfs(v) 调用返回后，意味着从 v 出发的所有"死胡同"都已探明。我们必须把 v 从"记事本"中擦掉，"回退"到 u，然后才能在 for 循环的下一次迭代中，去探索 u 的下一个邻居。

代码实现 (O(N * 2^N) 时间, O(N) 空间)

C++

复制代码

#include <vector>

using namespace std;

class Solution {
private:
    vector<vector<int>> allPaths; // 存储最终所有路径
    vector<int> currentPath;      // 存储当前正在探索的路径
    int targetNode;
    vector<vector<int>> graph_copy; // 存储图的拷贝

    void dfs(int u) {
        // 1. 检查是否到达终点
        if (u == targetNode) {
            allPaths.push_back(currentPath);
            return;
        }

        // 2. 探索所有邻居
        for (int v : graph_copy[u]) {
            // "做选择"：前进到 v
            currentPath.push_back(v);
            // 递归探索
            dfs(v);
            // "撤销选择"：回溯，从 v 退回到 u
            currentPath.pop_back();
        }
    }

public:
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        int n = graph.size();
        targetNode = n - 1;
        graph_copy = graph;
        
        // 0. 起点入栈
        currentPath.push_back(0);
        
        // 启动 DFS
        dfs(0);
        
        return allPaths;
    }
};

深度复杂度分析

V (Vertices) ：顶点数 n。
E (Edges)：边数。
时间复杂度 O(N * 2^N) (其中 N 是 V)：
- 这是一个 DAG。在最坏的情况下（比如一个"全连接"的DAG），从 0 到 n-1 的路径数量可以达到指数级 O(2^(N-2))。
- 我们假设总共有 P 条路径。
- 每找到一条路径，我们需要 O(N) 的时间将 currentPath 复制到 allPaths 中。
- DFS 遍历本身（探索所有可能的边）的时间消耗与 P 和 N 相关。
- 一个粗略但被广泛接受的上限是 O(N * 2^N)。
空间复杂度 O(N)：
- currentPath 向量：在最坏情况下，存储一条从 0 到 n-1 的路径，长度为 N。
- 递归栈 ：DFS 的递归深度，在 DAG 中最多为 N。
- （注意：allPaths 作为输出，其空间 O(P * N) 通常不计入算法的"额外空间复杂度"）
- 总空间复杂度 O(N + N) = O(N)。

总结

今天，我们为 DFS 装备了强大的"回溯"能力。

DFS：提供了"一条路走到黑"的探索框架。
currentPath.push_back(v)：是"做选择"。
currentPath.pop_back() ：是"撤销选择"（即回溯）。

这套"选择-递归-撤销 "的三部曲，是解决所有"排列、组合、子集、路径枚举"类问题的"万能模板"。

在下一篇中，我们将把今天学到的 DFS/BFS，应用到最常见的"隐式图"------二维网格（"岛屿问题"）上！

下期见！