12月力扣每日一题（划分dp + 单调栈 + 堆 + 会议安排）

目录

[3578. 统计极差最大为 K 的分割方式数 划分dp + 滑动窗口](#3578. 统计极差最大为 K 的分割方式数 划分dp + 滑动窗口)

[960. 删列造序 III 最长上升子序列 多行版](#960. 删列造序 III 最长上升子序列 多行版)

[2054. 两个最好的不重叠活动 单调栈 + 二分](#2054. 两个最好的不重叠活动 单调栈 + 二分)

[1751. 最多能得到的会议价值 II dp（上一问两个会议的加强版）](#1751. 最多能得到的会议价值 II dp（上一问两个会议的加强版）)

[2402. 会议室 III 堆 + 模拟](#2402. 会议室 III 堆 + 模拟)

[2141. 同时运行 N 台电脑的最长时间 后缀和](#2141. 同时运行 N 台电脑的最长时间 后缀和)

[2211. 统计道路上的碰撞次数 脑筋急转弯](#2211. 统计道路上的碰撞次数 脑筋急转弯)

---

3578. 统计极差最大为 K 的分割方式数 划分dp + 滑动窗口

将 nums 分割成 连续子段，使得每个子段的 最大值 与 最小值 之间的差值 不超过 k 的方案数。

f [i+1] 为 0~i 之间数组划分种类数。 划分 dp 状态转移：可以从哪些位置 j 转移过来。

j 和 i 要比较近，越远数组元素越多，最小更小最大更大，差值更大。

需要知道 i 往前最长的 符合最大最小差值的长度 L（可用滑动窗口维护）

总方案数 即为可转移位置的方案数求和 。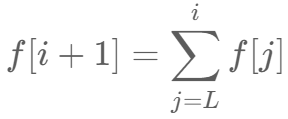

分别滑动窗口维护 最大/最小值，队列头一直是 最大/最小。 sum_f 一直维护这一段的求和。

根据滑动窗口本身 + 差值不超过 K，出队两次。

class Solution:
    def countPartitions(self, nums: List[int], k: int) -> int:
        n, left, sum_f, MOD = len(nums), 0, 0, 1_000_000_007
        min_q, max_q = deque(), deque()
        f = [1] + [0] * (n)

        for i, x in enumerate(nums):
            # 1. 滑动窗口入
            sum_f += f[i]

            while min_q and x <= nums[min_q[-1]]:
                min_q.pop()
            min_q.append(i)

            while max_q and x >= nums[max_q[-1]]:
                max_q.pop()
            max_q.append(i)

            # 2. 差值不超过 K
            while nums[max_q[0]] - nums[min_q[0]] > k:
                sum_f -= f[left]
                left += 1
                if min_q[0] < left:
                    min_q.popleft()
                if max_q[0] < left:
                    max_q.popleft()

            # 3. 更新答案
            f[i + 1] = sum_f % MOD

        return f[n]

960. 删列造序 III 最长上升子序列 多行版

最少删除几列，可以使得每行都是非递减的。

1行 的最长非递减子序列：dp[i] 为以 i 位置结束的最长 ，由前面的 j 符合 a[j] ≤ a[i], max(dp[j])+1

n 行 则判断条件变成 all（每行都小于等于）

最少需要删的 -> m - 保留最长

class Solution:
    def minDeletionSize(self, strs: List[str]) -> int:
        m = len(strs[0])
        f = [0] * m
        for i in range(m):
            for j in range(i):
                if f[j] > f[i] and all(s[j] <= s[i] for s in strs): # 可以转换
                    f[i] = f[j]
            f[i] += 1
        return m - max(f)

2054. 两个最好的不重叠活动 单调栈 + 二分

选定后一个活动后，前一个活动是 {结束时间在此之前} 里价值最高的。

单调栈维护结束时间在此之前 ，每一时刻价值最高的

（时间靠后 价值又低 的 不会入栈 ）先对结束时间排序 ，每次循环 价值高于栈顶才入栈。

在此之前价值最高 -> 对应结束时间最晚 ->二分

class Solution:
    def maxTwoEvents(self, events: List[List[int]]) -> int:
        # 按照结束时间排序
        events.sort(key=lambda e: e[1])  

        # 从栈底到栈顶，结束时间递增，价值递增
        st = [(0, 0)]  # 栈底哨兵 
        ans = 0
        for start_time, end_time, value in events:
            # 二分查找最后一个结束时间 < start_time 的活动
            i = bisect_left(st, (start_time,)) - 1
            ans = max(ans, st[i][1] + value)
            # 遇到比栈顶更大的价值，入栈
            if value > st[-1][1]:
                st.append((end_time, value))
        return ans

1751. 最多能得到的会议价值 II dp（上一问两个会议的加强版）

会议有 [开始，结束，价值]，最多参加 k 个 不重叠会议能获得的价值。

dp[i][j] 为以 第 i 个会议结束 ，总共参加 j 个会议的最大价值。（关于 i，j 都单调递增）

按结束时间从前到后 排序+枚举；二分 找上一个结束时间最晚的 状态转移。

class Solution:
    def maxValue(self, events: List[List[int]], k: int) -> int:
        events.sort(key=lambda e:e[1])
        n = len(events)
        dp = [[0]*(k+1) for _ in range(n+1)]
        for i,(s,_,v) in enumerate(events):
            l = bisect_left(events,s,hi=i,key=lambda e:e[1]) # 上一个结束最晚的
            for j in range(1,k+1): # 枚举总会议次数
                dp[i+1][j] = max(dp[i][j],dp[l][j-1]+v)
        return dp[n][k]

2402. 会议室 III 堆 + 模拟

堆1（哪些会议室 空闲 编号最小的）堆2 （每个会议室结束时间 结束的最早）

按开始时间从前到后处理会议；先把已经结束的会议室释放；

有空的会议室 则编号最小 ；否则预定结束时间最早的那个；

统计对应会议室的会议数量 cnt ++

class Solution:
    def mostBooked(self, n: int, meetings: List[List[int]]) -> int:
        meetings.sort(key=lambda m: m[0])

        idle = list(range(n))  # 会议室编号
        using = []  # (结束时间，会议室编号)
        cnt = [0] * n  # 会议室的开会次数

        for start, end in meetings:
            # 在 start 时刻空出来的会议室
            while using and using[0][0] <= start:
                heappush(idle, heappop(using)[1])

            if idle:  # 有空闲的会议室
                i = heappop(idle)
            else:  # 没有空闲的会议室
                e, i = heappop(using)  # 弹出一个最早结束的会议室（若有多个同时结束，弹出编号最小的会议室）
                end += e - start  # 更新当前会议的结束时间

            heappush(using, (end, i))  # 使用一个会议室
            cnt[i] += 1

        return cnt.index(max(cnt))

2141. 同时运行 N 台电脑的最长时间 后缀和

给定若干电池容量，给 N 台电脑最多同时供电时长。（先设答案为 x）

关键：则每个大于 x 的电池 容量再大也最多供电了 x ；对于容量本身低于 x 的电池，需要合并拼凑。

即找最大的 x；使得 ≥ x 的电池数 cnt1；与＜ x 的电池容量拼凑 sum / N = cnt2；cnt1 + cnt2 ≥ N。

对电池容量排序后，找临界的 i；把前 i 大的电池为单独充，后面的 sum 为合并充。

class Solution:
    def maxRunTime(self, n: int, batteries: List[int]) -> int:
        batteries.sort(reverse=True)
        s = sum(batteries)
        for b in batteries:
            if b <= s // n:
                return s // n
            s -= b
            n -= 1

2211. 统计道路上的碰撞次数 脑筋急转弯

• 当两辆移动方向 相反 的车相撞时，碰撞次数加 2 。
• 当一辆移动的车和一辆静止的车相撞时，碰撞次数加 1 。
• 碰撞后留在原地

根据这些性质得：

1. 去掉前缀向左开、后缀向右开的车后，剩下的车必然会碰撞。

2. 贡献值只来自于移动的车 ，每辆移动的车贡献1。

class Solution:
    def countCollisions(self, s: str) -> int:
        s = s.lstrip('L')  # 前缀向左的车不会发生碰撞
        s = s.rstrip('R')  # 后缀向右的车不会发生碰撞
        return len(s) - s.count('S')  # 剩下非静止的车必然会碰撞