在编程世界里,有不少经典问题既能考验逻辑思维,又能帮助我们深入理解编程语言的核心特性,汉诺塔就是其中之一。而 C 语言作为一门贴近底层、逻辑严谨的编程语言,用它来实现汉诺塔解法,不仅能让我们掌握递归这一重要编程思想,还能加深对函数调用、流程控制的理解。今天,我们就一起来拆解汉诺塔问题,看看如何用 C 语言一步步实现它的求解过程。
一、汉诺塔问题:古老传说背后的编程挑战
汉诺塔问题源自一个古老的印度传说:有三根柱子(通常标记为 A、B、C)和若干个大小不同的盘子,初始时所有盘子都套在 A 柱上,且盘子按从大到小的顺序叠放。我们的目标是将所有盘子从 A 柱移到 C 柱,移动过程中要遵守两个规则:一是每次只能移动一个盘子;二是任何时候都不能让一个较大的盘子放在一个较小的盘子上面。
看似简单的规则,实则藏着精妙的逻辑。当盘子数量较少时(比如 1 个或 2 个),我们很容易想出移动步骤,但随着盘子数量增加,步骤会呈指数级增长。这时候,递归思想就成了破解问题的关键 ------ 将复杂的大问题拆解成多个结构相同的小问题,直到问题简单到可以直接解决。
二、C 语言实现汉诺塔:代码拆解与逻辑分析
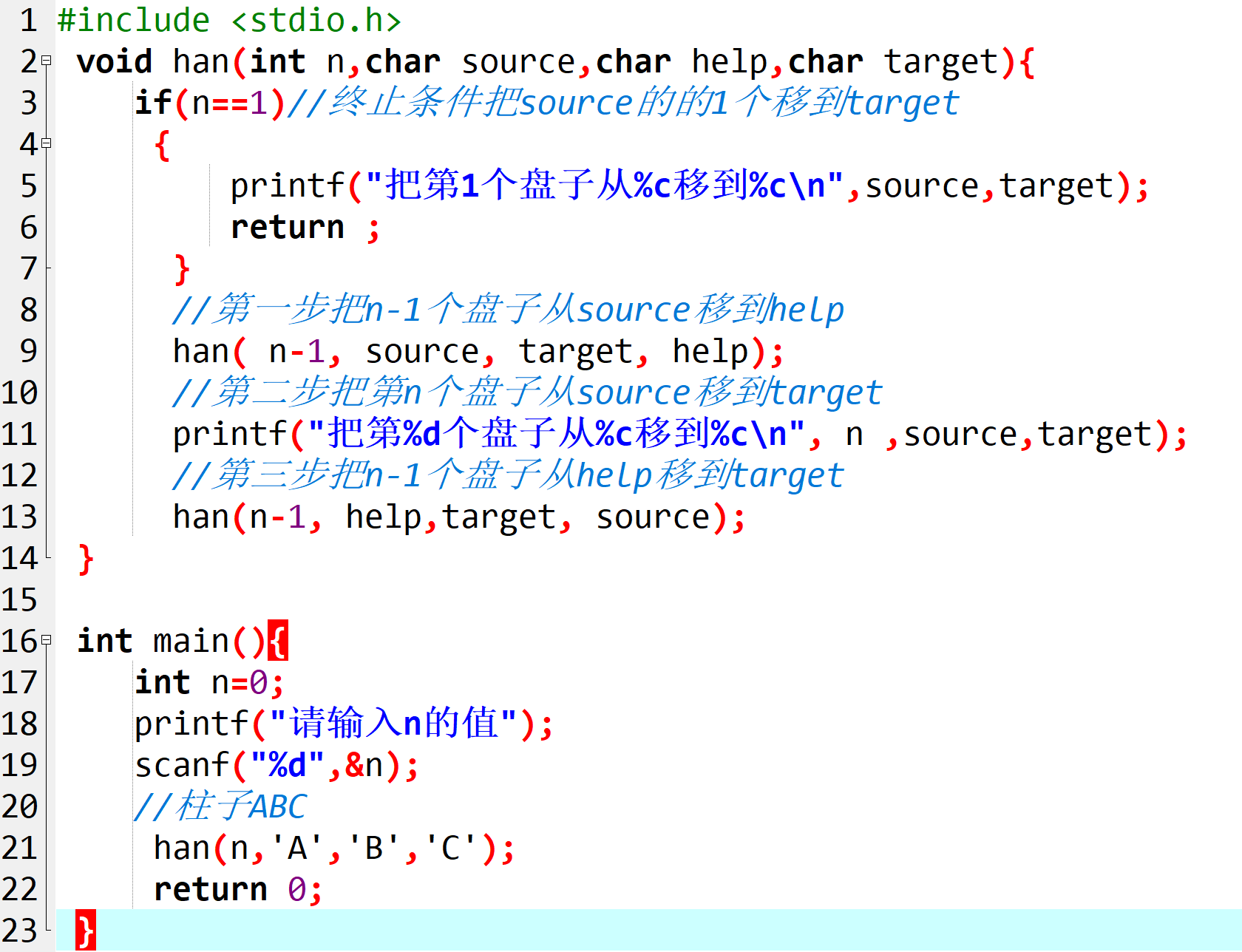
接下来,我们结合一段完整的 C 语言代码,逐行解析汉诺塔的实现逻辑。先看完整代码:
#include <stdio.h>
void han(int n,char source,char help,char target){
if(n==1)//终止条件:把source的1个盘子移到target
{
printf("把第1个盘子从%c移到%c\n",source,target);
return ;
}
//第一步:把n-1个盘子从source移到help
han( n-1, source, target, help);
//第二步:把第n个盘子从source移到target
printf("把第%d个盘子从%c移到%c\n", n ,source,target);
//第三步:把n-1个盘子从help移到target
han(n-1, help, target, source);
}
int main(){
int n=0;
printf("请输入n的值");
scanf("%d",&n);
//柱子ABC
han(n,'A','B','C');
return 0;
}
1. 头文件与函数定义:搭建程序框架
代码开头的#include <stdio.h>是 C 语言的标准输入输出头文件,因为我们需要用printf打印移动步骤、用scanf获取用户输入的盘子数量,所以必须包含这个头文件。
接着定义了一个名为han的函数,它有 4 个参数:
- int n:表示当前需要移动的盘子数量;
- char source:表示盘子的 "源柱子"(即盘子当前所在的柱子);
- char help:表示 "辅助柱子"(用于临时存放盘子的柱子);
- char target:表示 "目标柱子"(即盘子要移到的柱子)。
这个函数的核心作用,就是根据传入的参数,输出从源柱子到目标柱子的移动步骤。
2. 递归终止条件:解决最小问题
递归的关键是 "终止条件"------ 当问题拆解到最小规模时,直接给出答案,避免无限递归。在汉诺塔问题中,最小规模就是 "只有 1 个盘子",这时候不需要辅助柱子,直接把盘子从源柱子移到目标柱子即可。
所以代码中的if(n==1)就是终止条件:当n=1时,执行printf打印 "把第 1 个盘子从源柱子移到目标柱子",然后用return结束当前函数调用,回到上一层递归。
3. 递归核心逻辑:拆解问题的三步法
当n>1时,函数会按照 "三步法" 拆解问题,这也是汉诺塔递归思想的核心:
- 第一步:调用han(n-1, source, target, help)------ 把上面n-1个盘子从 "源柱子" 移到 "辅助柱子",此时 "目标柱子" 临时充当辅助角色。这一步的目的是腾出最下面的第n个盘子(最大的盘子),让它能直接移到目标柱子。
- 第二步:执行printf("把第%d个盘子从%c移到%c\n", n ,source,target)------ 此时源柱子上只剩下最大的第n个盘子,直接把它从源柱子移到目标柱子,这一步是整个过程中 "最关键的一步",也是唯一不需要递归的步骤。
- 第三步:调用han(n-1, help, target, source)------ 把之前移到 "辅助柱子" 上的n-1个盘子,从 "辅助柱子" 移到 "目标柱子",此时 "源柱子" 临时充当辅助角色。这一步完成后,所有盘子就都从源柱子移到了目标柱子,问题解决。
4. main 函数:程序的入口与交互
main函数是 C 语言程序的入口,负责获取用户输入并调用han函数:
- 先定义变量n存储盘子数量,初始化为 0;
- 用printf提示用户输入n的值,再用scanf读取用户输入;
- 最后调用han(n,'A','B','C'),明确初始时源柱子是 A、辅助柱子是 B、目标柱子是 C,启动递归求解过程。
三、代码运行效果:直观感受递归的魔力
为了让大家更直观地理解代码的作用,我们以 "输入 n=3" 为例,看看程序的输出结果:
请输入n的值3
把第1个盘子从A移到C
把第2个盘子从A移到B
把第1个盘子从C移到B
把第3个盘子从A移到C
把第1个盘子从B移到A
把第2个盘子从B移到C
把第1个盘子从A移到C
这个输出完美符合 3 个盘子的汉诺塔移动步骤:先把上面 2 个盘子从 A 移到 B(前 3 步),再把最大的第 3 个盘子从 A 移到 C(第 4 步),最后把 B 柱上的 2 个盘子移到 C(后 3 步)。每一步都严格遵守 "不能把大盘放小盘上" 的规则,这就是递归思想的魔力 ------ 不需要我们手动规划每一步,程序会自动拆解并执行。
四、总结:递归思想与 C 语言的契合之处
通过用 C 语言实现汉诺塔,我们能深刻感受到递归思想的魅力:它让复杂问题变得 "可拆解",让代码更简洁、逻辑更清晰。而 C 语言对函数调用的良好支持,也为递归提供了坚实的基础 ------ 每次递归调用han函数时,参数会重新传递,函数栈会自动保存当前的执行状态,直到触发终止条件后再逐层返回。
对于初学者来说,理解递归可能需要一些时间,建议大家可以尝试修改代码中的盘子数量(比如 n=2、n=4),观察输出结果的变化,或者在纸上手动模拟递归过程。相信通过不断实践,你不仅能掌握汉诺塔的解法,还能将递归思想运用到更多编程问题中,比如斐波那契数列、二叉树遍历等。
C 语言的魅力就在于此 ------ 它不只是一门编程语言,更是一种解决问题的工具。而汉诺塔这样的经典问题,就是我们锻炼逻辑思维、提升编程能力的绝佳练手项目。希望今天的分享,能让你对 C 语言和递归思想有更深的理解!