核心思路
股票最大利润问题的核心是 "低买高卖",且仅允许一次交易(买入后需在未来不同日期卖出)。核心逻辑可概括为:
对于每个潜在卖出日,必须找到其之前(买入需在卖出前)的最低买入价,才能计算当前卖出日的最大利润;
遍历过程中动态维护两个关键信息:历史最低买入价、截至当前的最大利润;
无需暴力枚举所有 "买入 - 卖出" 组合,通过一次遍历即可同步更新最低买入价和最大利润,避免冗余计算。
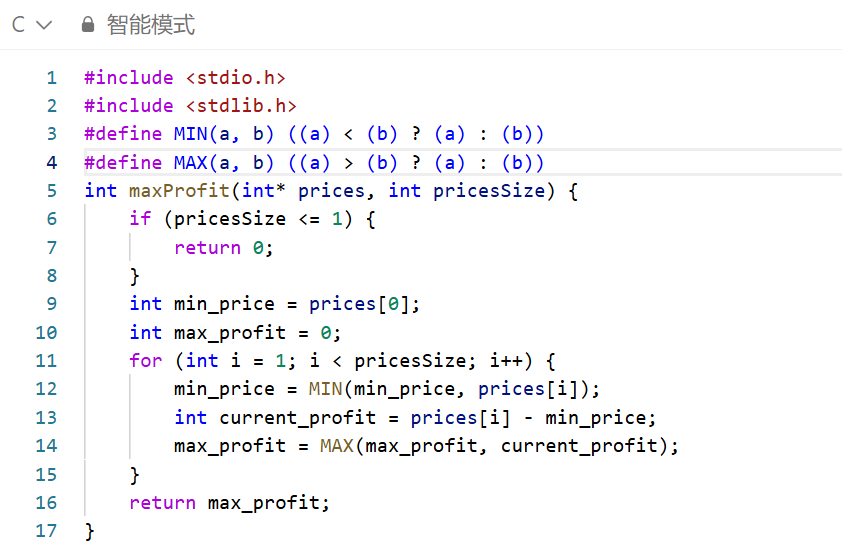
方法(一次遍历法 / 贪心思想)
初始化变量:
min_price:初始化为数组第一个元素,记录遍历至今的最低股票价格(代表最优买入时机);
max_profit:初始化为 0,记录遍历至今的最大利润(未找到盈利交易时返回 0)。
遍历数组(从第二个元素开始,索引 i=1):
第一步:更新 min_price,对比当前价格 prices[i] 与历史最低价格,取较小值(确保买入价始终为当前最优);
第二步:计算当前卖出利润 current_profit = prices[i] - min_price(以当前价格卖出,基于历史最低买入价的利润);
第三步:更新 max_profit,对比当前利润与历史最大利润,取较大值(保留最优盈利结果)。
返回结果:遍历结束后,max_profit 即为最大可获取利润,若为 0 则表示无盈利交易(如价格持续下跌)。
优点
时间效率极高:仅需一次遍历数组,时间复杂度为 O (n)(n 为数组长度),适用于题目中 10^5 级别的数据规模,无超时风险;
空间复杂度极低:仅使用两个额外变量(min_price 和 max_profit),空间复杂度为 O (1),内存占用可忽略;
逻辑简洁易懂:无需复杂数据结构或递归,核心逻辑围绕 "动态更新最优买入价和最大利润" 展开,代码易写易调试;
鲁棒性强:自动处理边界情况(如数组长度为 1、价格持续下跌、价格持续上涨等),无需额外判断逻辑。
结论
该方法通过 "一次遍历 + 贪心思想",完美解决了 "一次股票交易最大利润" 问题,是该问题的最优解法;
核心优势在于用线性时间和常数空间替代了暴力枚举的 O (n²) 时间复杂度,在大规模数据下表现优异;
适用场景明确:仅允许一次交易、需快速计算最优买卖时机的场景,代码可直接复用,且易于扩展到类似的 "最优差值" 问题;
本质是通过 "贪心" 策略,在每一步都做出局部最优选择(更新最低买入价、保留最大利润),最终得到全局最优解,逻辑严谨且高效。