LeetCode 98. 验证二叉搜索树 解题总结

目录

一、方法一：递归边界约束法（范围校验）

[1. 核心思想](#1. 核心思想)

[2. 完整实现代码](#2. 完整实现代码)

[3. 重点 & 难点](#3. 重点 & 难点)

[二、方法二：中序遍历法（利用 BST 特性）](#二、方法二：中序遍历法（利用 BST 特性）)

[1. 核心思想](#1. 核心思想)

[2. 实现代码](#2. 实现代码)

[版本 1：递归中序遍历（简洁易理解）](#版本 1：递归中序遍历（简洁易理解）)

[版本 2：迭代中序遍历（避免递归栈溢出）](#版本 2：迭代中序遍历（避免递归栈溢出）)

[3. 重点 & 难点](#3. 重点 & 难点)

三、两种方法对比

四、常见易错点总结

五、总结

---

验证二叉搜索树（BST）是二叉树高频面试题，核心考点是准确理解 BST 的定义（左子树所有节点值 <根节点值，右子树所有节点值> 根节点值，且左右子树也必须是 BST），而非仅 "根节点大于左孩子、小于右孩子"。以下总结两种主流解法，涵盖核心思想、实现、重点难点及对比。

一、方法一：递归边界约束法（范围校验）

1. 核心思想

基于 BST 的定义，为每个节点划定合法取值范围（左边界 < 节点值 < 右边界）：

• 根节点的初始范围是 (Long.MIN_VALUE, Long.MAX_VALUE)（用 Long 避免 int 极值溢出）；
• 递归遍历左子树时，更新右边界为当前节点值（左子树所有节点必须 < 当前节点）；
• 递归遍历右子树时，更新左边界为当前节点值（右子树所有节点必须 > 当前节点）；
• 若所有节点都满足范围约束，则为合法 BST。

2. 完整实现代码

class Solution {
    // 递归函数：校验当前节点是否在(left, right)范围内，且子树满足BST
    private boolean isValidBSTHelper(TreeNode root, long left, long right) {
        if (root == null) return true; // 空树是合法BST
        long curVal = root.val;
        // 核心：当前节点超出范围 → 不合法；递归校验左右子树
        if (curVal <= left || curVal >= right) return false;
        return isValidBSTHelper(root.left, left, curVal) // 左子树范围：(left, curVal)
                && isValidBSTHelper(root.right, curVal, right); // 右子树范围：(curVal, right)
    }

    public boolean isValidBST(TreeNode root) {
        // 初始范围用Long极值，避免int最大值/最小值的溢出问题
        return isValidBSTHelper(root, Long.MIN_VALUE, Long.MAX_VALUE);
    }
}

注：个人暂时感觉这个思路好理解一点；很多方法其实只需要记一种，然后面试的时候思路清晰就OK

3. 重点 & 难点

• 重点 ：
  • 范围约束需覆盖 "子树所有节点"，而非仅直接子节点；
  • 用Long类型替代int作为边界，解决Integer.MAX_VALUE/Integer.MIN_VALUE作为节点值时的校验失效问题（如测试用例[2147483647]）。
• 难点 ：
  • 容易误将边界设为Integer极值，导致极端值校验失败；
  • 递归时边界更新方向易混淆（左子树更新右边界，右子树更新左边界）。

二、方法二：中序遍历法（利用 BST 特性）

1. 核心思想

BST 的核心特性：中序遍历结果是严格递增的序列（左→根→右，值从小到大）。

• 遍历过程中记录前一个节点的值；
• 若当前节点值 ≤ 前一个节点值，说明不满足递增特性，不是合法 BST；
• 遍历完成后未发现违规，则为合法 BST。

2. 实现代码

版本 1：递归中序遍历（简洁易理解）

class Solution {
    private long preVal = Long.MIN_VALUE; // 记录前一个节点值，初始为Long最小值

    public boolean isValidBST(TreeNode root) {
        // 中序遍历：左→根→右
        if (root == null) return true;
        // 先遍历左子树，左子树不合法直接返回false
        if (!isValidBST(root.left)) return false;
        // 校验当前节点：若≤前一个值，不合法
        if (root.val <= preVal) return false;
        // 更新前一个节点值为当前值；注意此处应该递归到了最底层，从左子树最下面的节点开始的
        preVal = root.val;
        // 遍历右子树
        return isValidBST(root.right);
    }
}

版本 2：迭代中序遍历（避免递归栈溢出）

class Solution {
    public boolean isValidBST(TreeNode root) {
        if (root == null) return true;
        Deque<TreeNode> stack = new LinkedList<>();
        long preVal = Long.MIN_VALUE;
        TreeNode cur = root;
        
        // 迭代中序遍历模板
        while (cur != null || !stack.isEmpty()) {
            // 先遍历左子树，全部入栈
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            // 弹出栈顶（当前最左节点）
            cur = stack.pop();
            // 校验递增性
            if (cur.val <= preVal) return false;
            preVal = cur.val;
            // 遍历右子树
            cur = cur.right;
        }
        return true;
    }
}

3. 重点 & 难点

• 重点 ：
  • 利用 BST 中序递增的特性，将 "验证 BST" 转化为 "验证序列递增"，逻辑更直观；
  • 初始preVal需设为Long.MIN_VALUE，避免节点值为Integer.MIN_VALUE时误判。
• 难点 ：
  • 递归版需注意preVal的作用域（需设为成员变量 / 数组传递，避免递归栈覆盖）；
  • 迭代版需熟练掌握中序遍历的栈实现逻辑，避免节点遍历顺序错误。

三、两种方法对比

方法	时间复杂度	空间复杂度	核心优势	适用场景
递归边界约束法	O(n)	O(h)	直接贴合 BST 定义，逻辑严谨	需快速验证、递归深度可控
中序遍历法（递归）	O(n)	O(h)	利用 BST 特性，代码简洁	面试中快速手写、逻辑直观
中序遍历法（迭代）	O(n)	O(h)	避免递归栈溢出	处理深度极大的二叉树

（注：n 为节点数，h 为树的高度；平衡树 h=logn，斜树 h=n）

四、常见易错点总结

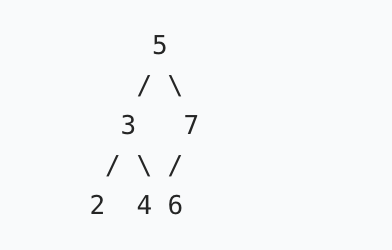
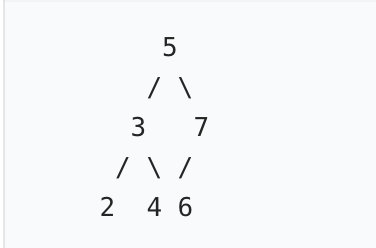
1. 边界类型错误 ：用int而非Long作为边界 / 前值，导致Integer.MAX_VALUE/Integer.MIN_VALUE测试用例失效；
2. BST 定义理解偏差 ：仅校验 "根> 左孩子、根 < 右孩子"，未约束整个子树的范围（如[5,1,4,null,null,3,6]会误判为合法）；
3. 中序遍历递增性错误：将 "严格递增" 写成 "非递减"（BST 不允许节点值相等）；
4. 递归边界更新错误：左子树更新左边界、右子树更新右边界（正确应为左子树更右边界，右子树更左边界）。

五、总结

• 递归边界法是 "从定义出发" 的通用解法，需重点掌握范围约束和类型溢出问题；

• 中序遍历法是 "利用特性的巧解"，核心是记住 BST 中序递增的关键性质；

• 面试中优先选择中序遍历（代码简洁），若面试官追问 "避免递归栈溢出"，可补充迭代版；若追问 "BST 定义的严格实现"，可补充递归边界法。

  ---