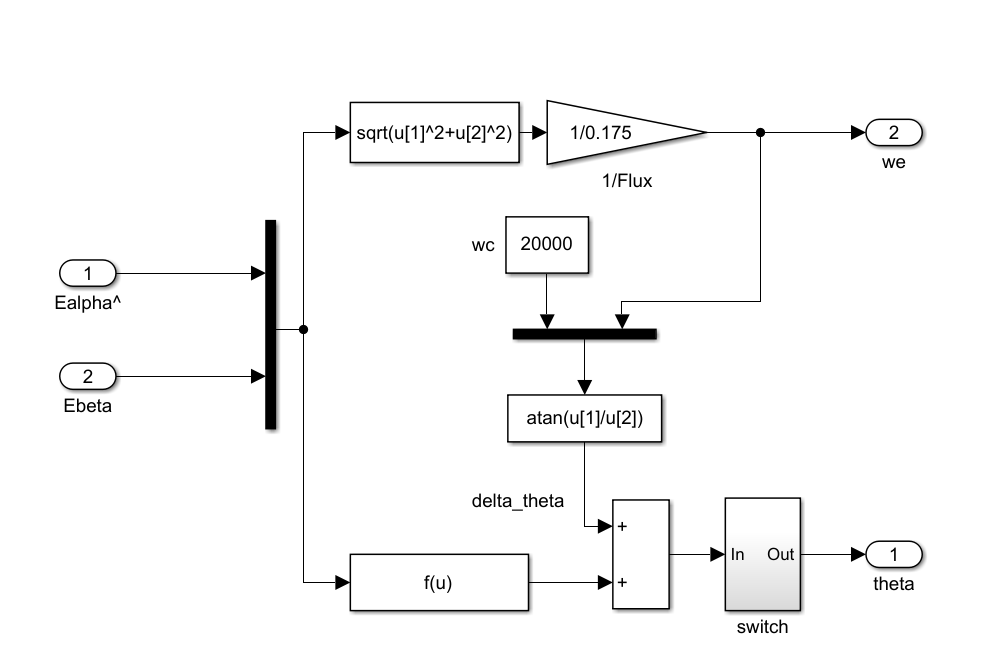
多的不说直接上图。
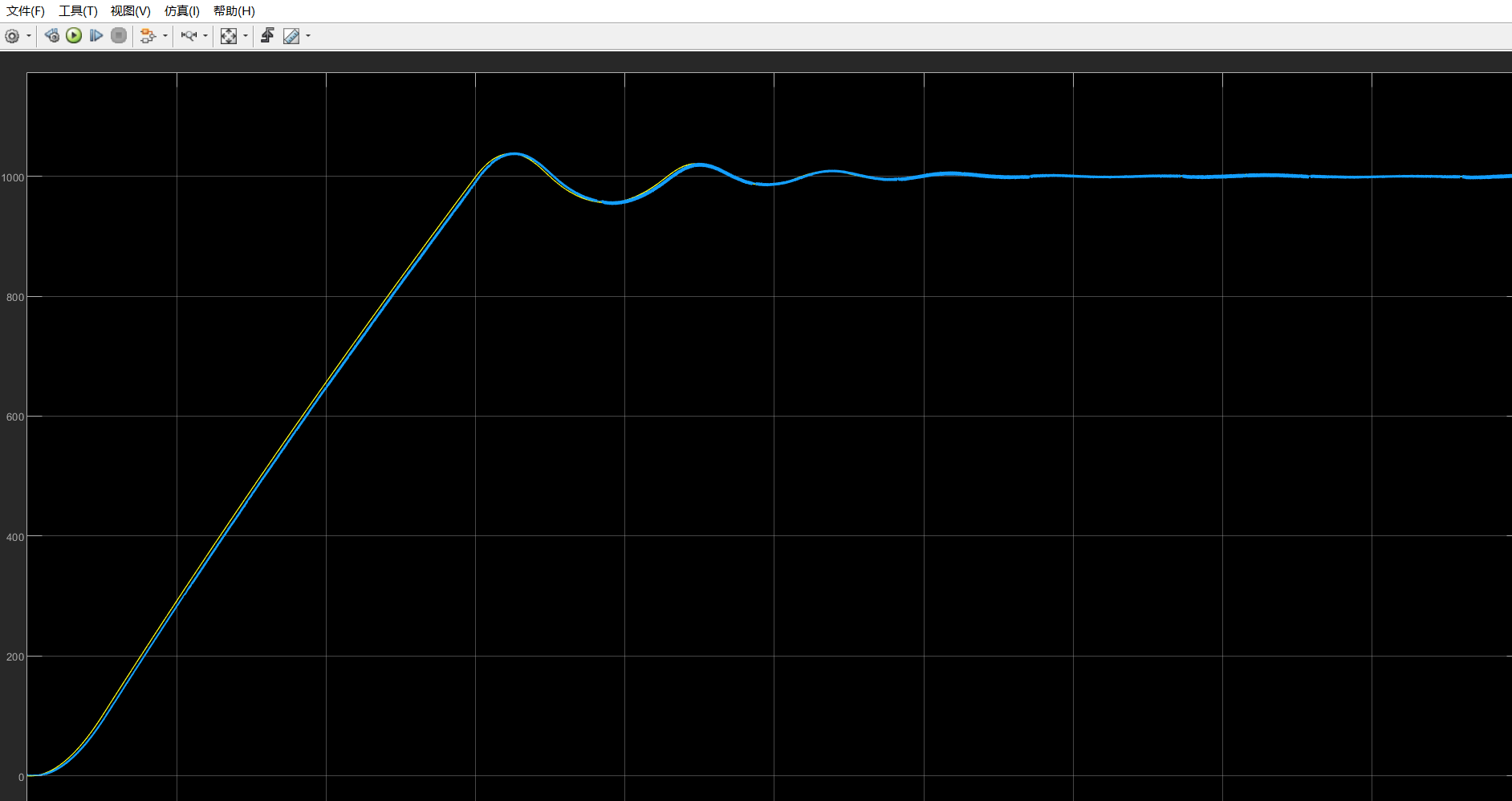
下面是速度的仿真结果。可以看到速度还是跟随的很准的。
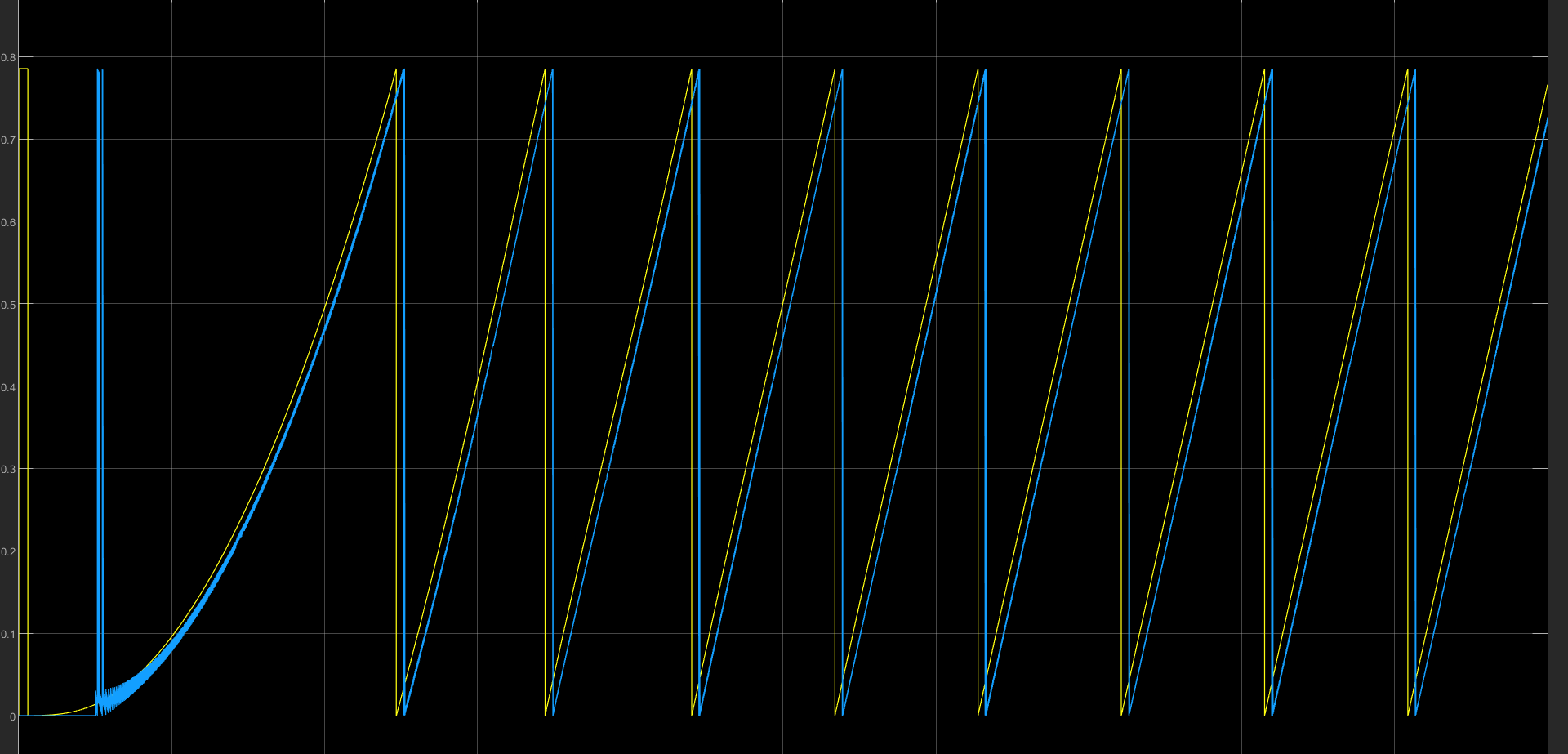
下面的是角度的。虽然说有一点偏差但是还是可以的
1.反park变化
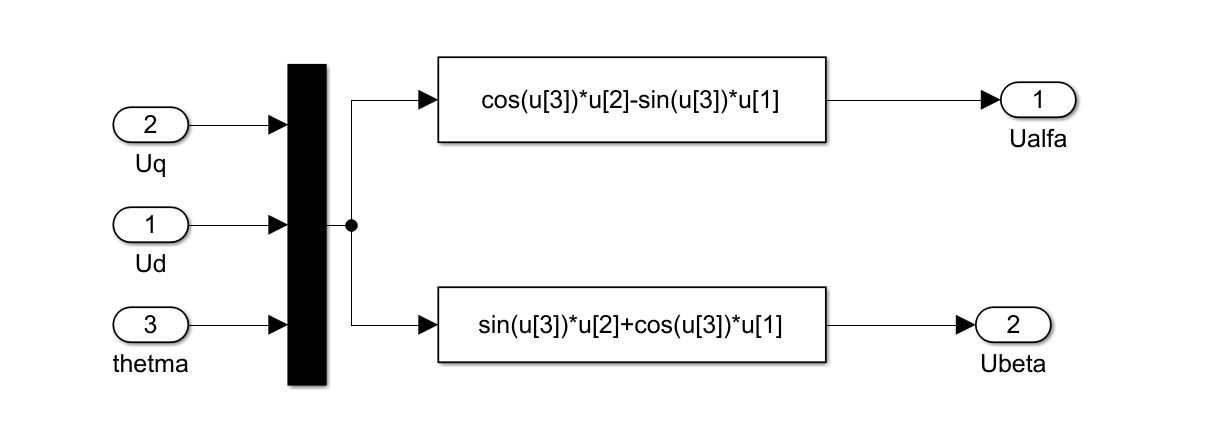
这个图是一个 坐标变换模块 ,具体是将电机在 dq 坐标系下的电压分量(Ud, Uq) 转换到 静止 α-β 坐标系下的电压分量(Ualfa, Ubeta)。
这属于 逆 Park 变换(Inverse Park Transform) 的一部分,也叫 dq 到 αβ 变换。
🔍 模块功能
✅ 输入:
Ud:d 轴电压(直轴电压)Uq:q 轴电压(交轴电压)thetma:转子电角度(即旋转坐标系相对于静止坐标系的夹角)
注意:
thetma是旋转坐标系的角度,通常由位置传感器或无传感器估计得到。
✅ 输出:
Ualfa:α 轴电压(静止坐标系)Ubeta:β 轴电压(静止坐标系)
📐 数学原理
该变换基于 旋转坐标系到静止坐标系的逆变换:
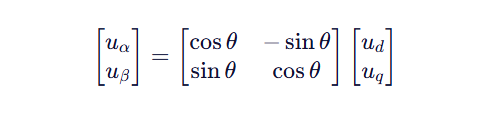
其中:
- θ=thetma
- ud=Ud
- uq=Uq
所以:
- uα=cos(θ)⋅uq−sin(θ)⋅ud
- uβ=sin(θ)⋅uq+cos(θ)⋅ud
2.逆Clarke+Svpwm
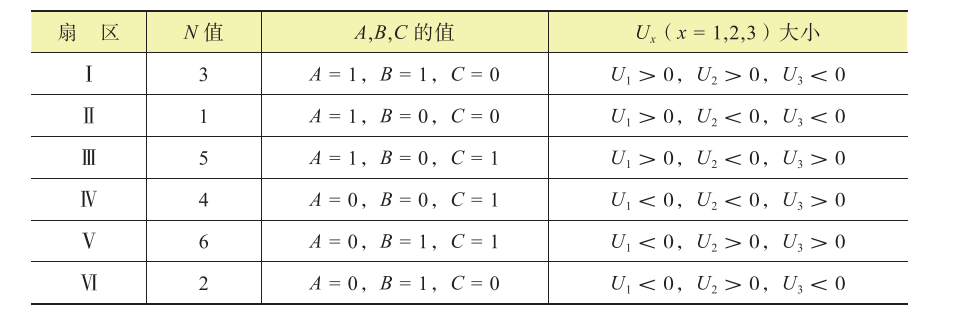
1.扇区判断
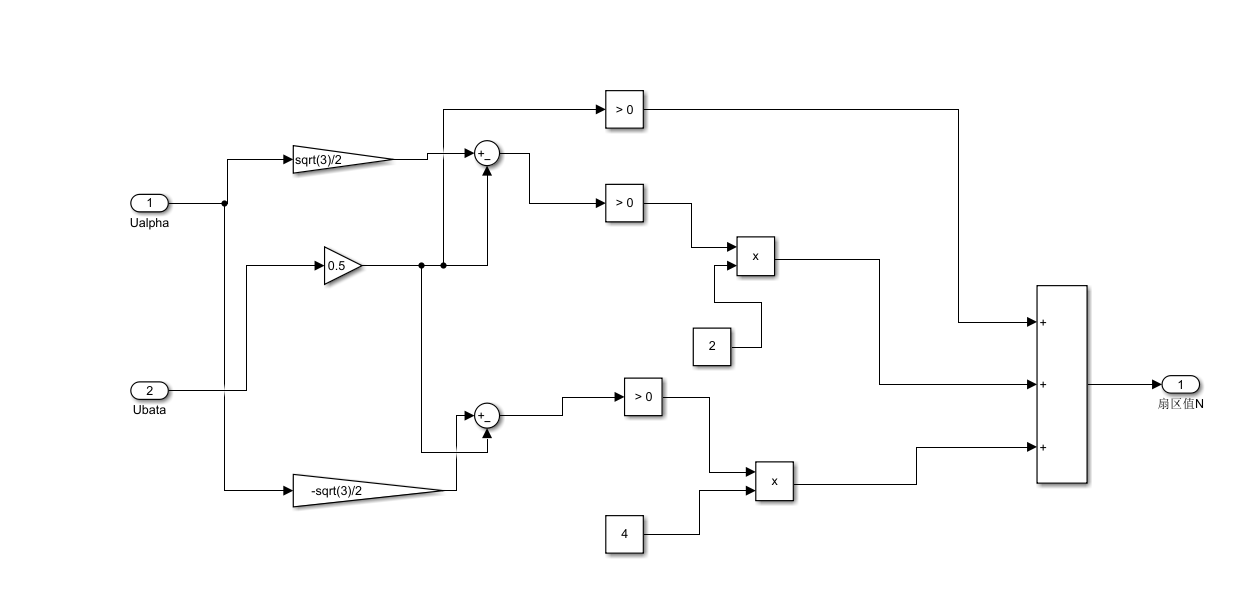
所在的扇区完全由Uβ、√3Uα-Uβ以及-(√3Uα +Uβ)决定。为了继续简化计算,做如下定义:
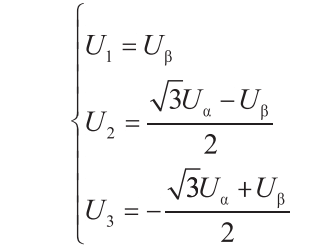
为了继续简化计算,我们规定:若U>0,则A=1,否则A=0;若U>0,则B=1,否则B=0;若U>0,则C=1,否则C=0。因此,A、B、C共有8种组合。但是,由表4.2可知,扇区计算中不存在A、B、C全是0或者全是1的状态,因此有效的4、B、C组合一共有6种。令N=A+2B+4C,通过A、B、C的不同组合计算出N值,可以很方便地判断矢量所处的扇区。表列出了N值与矢量所在扇区的对应关系。
2.逆clark
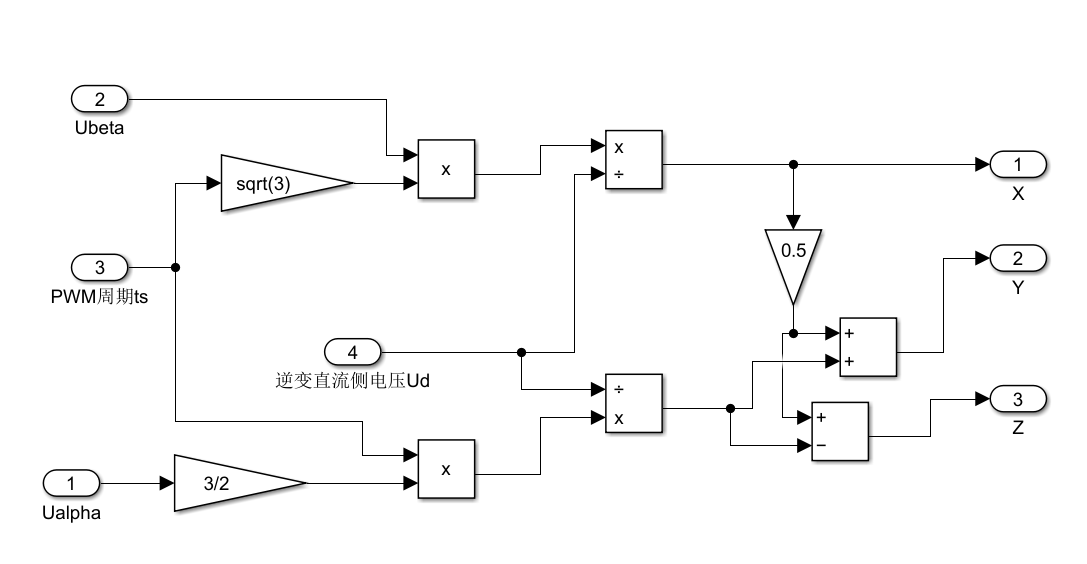
用于将 α-β 坐标系下的两相电压 转换为 三相静止坐标系下的电压(a、b、c 相)。这是电机控制中 SVPWM 或传统 PWM 调制的关键步骤。
✅ 功能概述
📌 模块名称:逆 Clarke 变换(αβ → abc)
🔧 输入:
Ualpha:α 轴电压分量Ubata(应为Ubeta):β 轴电压分量PWM周期ts:PWM 调制周期(可能用于后续定时或归一化)逆变直流侧电压Ud:直流母线电压(如 311 V)
⚠️ 注意:虽然输入了
Ud和ts,但标准的逆 Clarke 变换本身不依赖这两个参数。它们可能是为了后续 PWM 占空比计算而传递的。
🎯 输出:
X→ 对应 a 相电压 uaY→ 对应 b 相电压 ubZ→ 对应 c 相电压 uc
从 α-β 到 abc 的变换公式为:
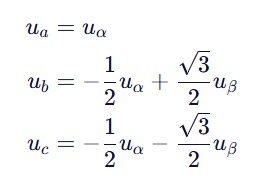
3.作用时间判断
✅ 这个仿真是干什么的?
这是一个用于 SVPWM(空间矢量脉宽调制)中,根据扇区编号 N 和 αβ 平面电压矢量分量 X、Y,计算两个基本电压矢量作用时间 T1 和 T2 的模块。
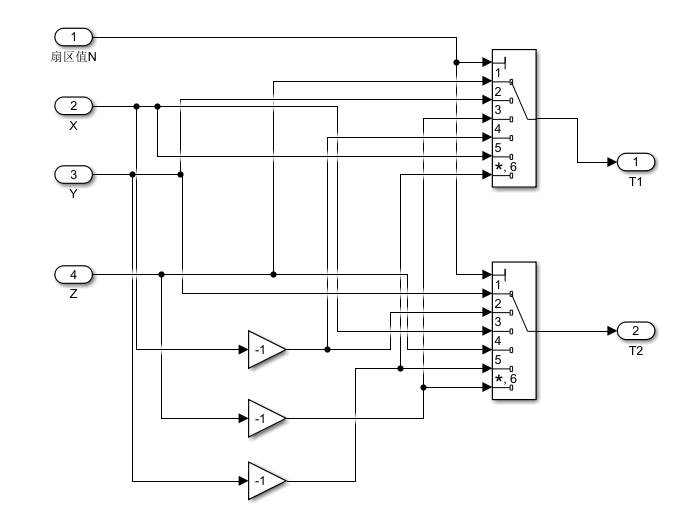

我的理解就是说,逆Clarke变换会计算出Va,Vb,Vc但是,我们只是需要其中是两项来合成我们需要的矢量,所以说,这里会根据扇区来选择我们需要的Va,Vb,Vc以及控制矢量的方向。下面是代码可以加深理解。
cpp
// ==================== 逆Clarke变换 ====================
// 将α-β坐标系电压转换为三相电压
// Va = Uβ
// Vb = -Uβ/2 + Uα*sqrt(3)/2
// Vc = -Uβ/2 - Uα*sqrt(3)/2
epwm->Va = epwm->Ubeta;
epwm->Vb = -(epwm->Ubeta >> 1) + ((((int32_t)epwm->Ualfa) * 0x0ddb) >> 12); // 0x0ddb ≈ sqrt(3)/2
epwm->Vc = -(epwm->Ubeta >> 1) - ((((int32_t)epwm->Ualfa) * 0x0ddb) >> 12);
// ==================== 扇区判断 ====================
// 根据三相电压的符号判断扇区
if (epwm->Va > 0) epwm->A = 1; else epwm->A = 0;
if (epwm->Vb > 0) epwm->B = 1; else epwm->B = 0;
if (epwm->Vc > 0) epwm->C = 1; else epwm->C = 0;
epwm->sector = epwm->A + (epwm->B << 1) + (epwm->C << 2); // 扇区号计算
// ==================== 时间计算 ====================
// 根据扇区计算各相导通时间
switch (epwm->sector)
{
case 1:
epwm->t1 = -epwm->Vb; // 扇区1的时间计算
epwm->t2 = -epwm->Vc;
break;
case 2:
epwm->t1 = -epwm->Vc; // 扇区2的时间计算
epwm->t2 = -epwm->Va;
break;
case 3:
epwm->t1 = epwm->Vb; // 扇区3的时间计算
epwm->t2 = epwm->Va;
break;
case 4:
epwm->t1 = -epwm->Va; // 扇区4的时间计算
epwm->t2 = -epwm->Vb;
break;
case 5:
epwm->t1 = epwm->Va; // 扇区5的时间计算
epwm->t2 = epwm->Vc;
break;
case 6:
epwm->t1 = epwm->Vc; // 扇区6的时间计算
epwm->t2 = epwm->Vb;
break;
default:
break;
}
4.过调制处理
输入信号:
| 编号 | 名称 | 含义 |
|---|---|---|
| 1 | T1 | 基本电压矢量 V1 的作用时间(原始计算值) |
| 2 | T2 | 基本电压矢量 V2 的作用时间(原始计算值) |
| 3 | TS | 载波周期(开关周期),即一个 PWM 周期的时间长度 |
⚠️ 注意:T1 和 T2 是从前面的"扇区选择 + 时间计算"模块输出的原始值,可能大于 TS,这就是"过调制"的表现。
为什么需要过调制处理?
正常情况(欠调制):
- 当参考电压矢量落在六边形内时,
T1 + T2 ≤ TS - 可以直接使用原始 T1、T2 值生成 PWM
- 输出电压与指令成比例
过调制情况(饱和):
- 当参考电压矢量超出六边形边界(即超过直流母线电压允许的最大幅值)
- 计算出的
T1 + T2 > TS - 若直接使用会导致:
- 开关时间超过周期 → 不可能实现
- 电机输出电压失真
- 控制失效
所以必须进行"过调制处理"。

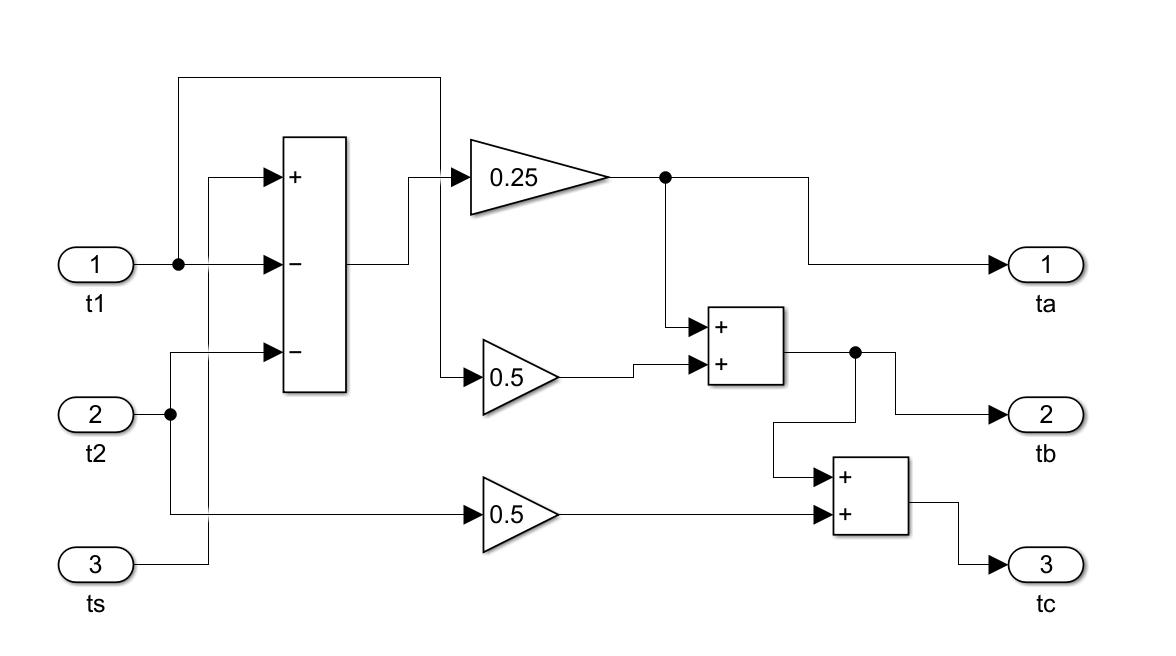
5.切换时间
SVPWM 中"切换时间计算"模块,用于将已经修正过的两个基本电压矢量作用时间 t1、t2,以及载波周期 ts,转换为 三相逆变器各桥臂的开关时刻(即 PWM 的导通/关断时间)。
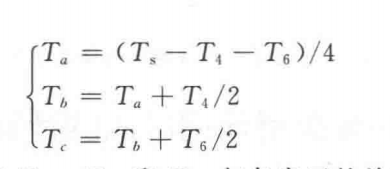
6.确定输出扇区
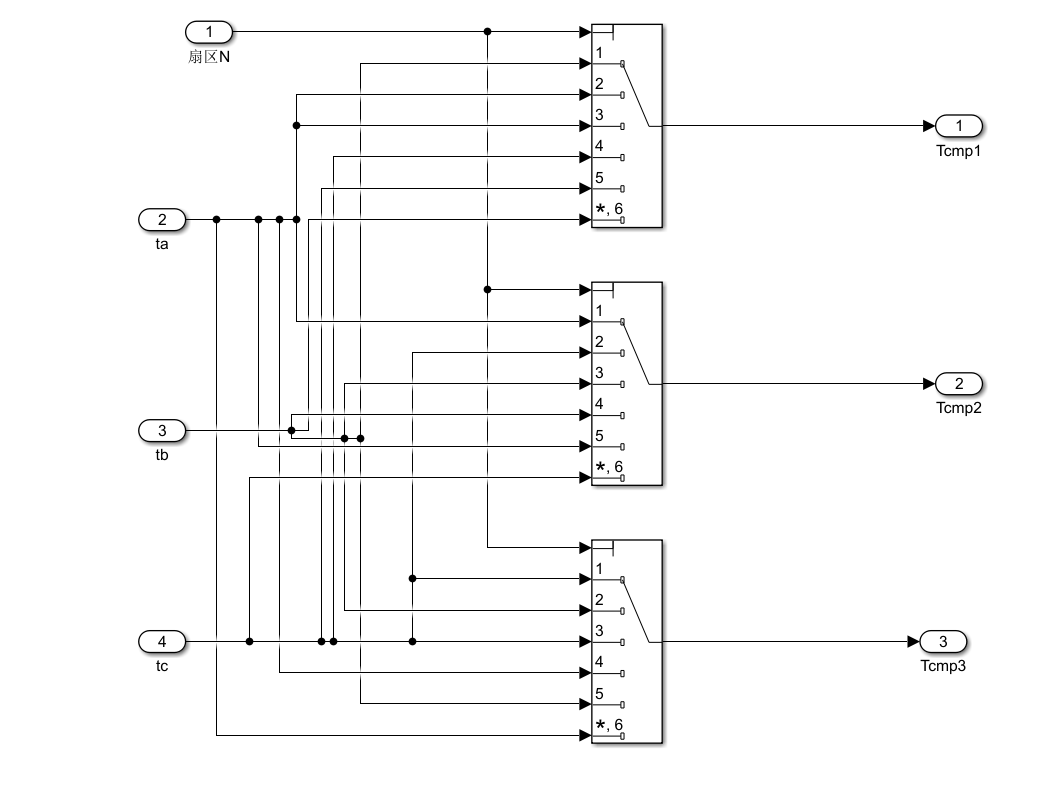
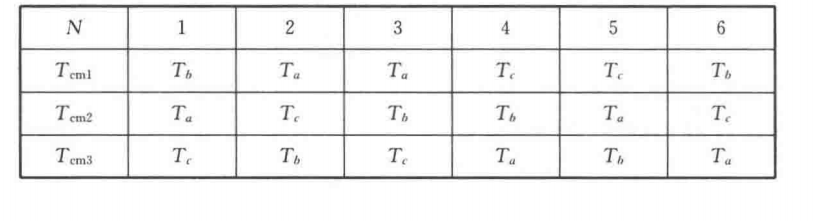
SVPWM 中"确定输出扇区"或"PWM 时序分配"模块,但它并不是用来"判断输入扇区"的,而是根据 已知的扇区 N 和三相 PWM 切换时间 ta、tb、tc,来生成三个中间变量 Tcmp1、Tcmp2、Tcmp3,用于后续的 比较器(Comparator)触发 PWM 波形。
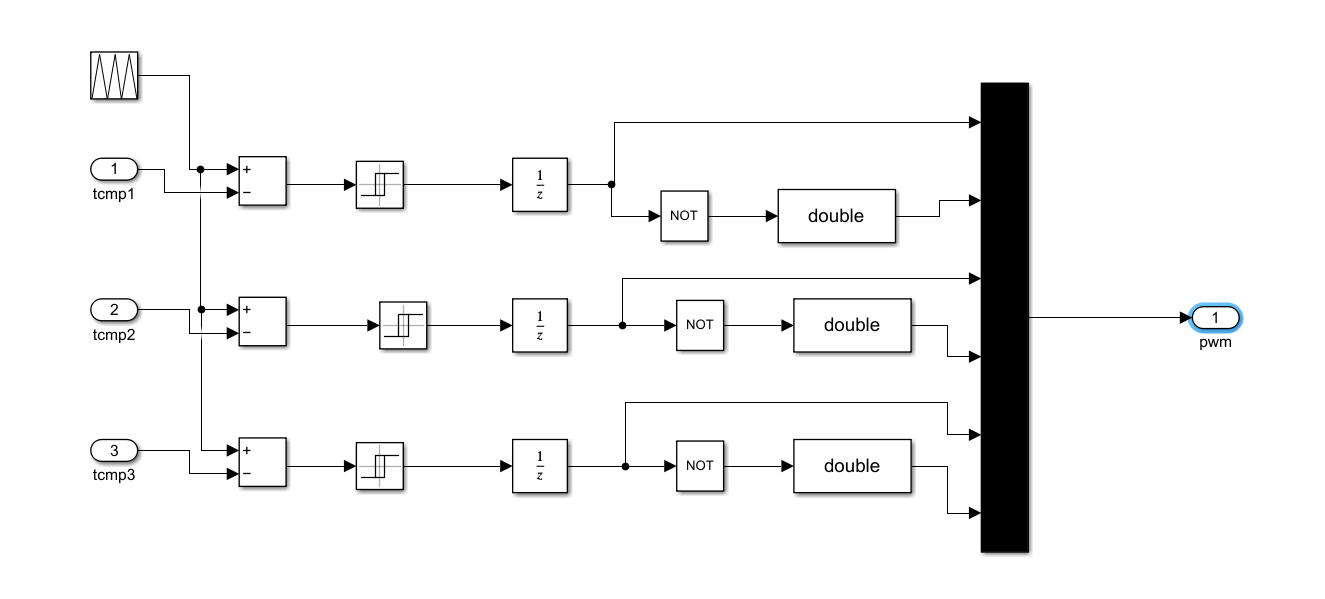
7.PWM信号产生
SVPWM 中"确定输出扇区"或"PWM 时序分配"模块,但它并不是用来"判断输入扇区"的,而是根据 已知的扇区 N 和三相 PWM 切换时间 ta、tb、tc,来生成三个中间变量 Tcmp1、Tcmp2、Tcmp3,用于后续的 比较器(Comparator)触发 PWM 波形。
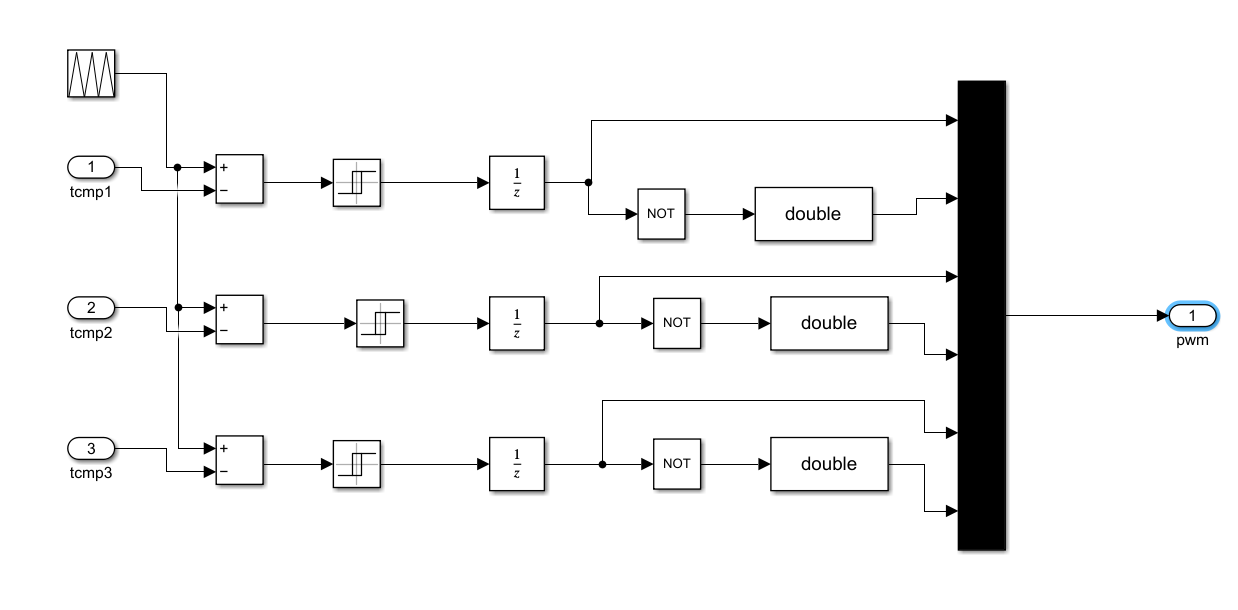
7.PWM信号产生
SVPWM 中"确定输出扇区"或"PWM 时序分配"模块,但它并不是用来"判断输入扇区"的,而是根据 已知的扇区 N 和三相 PWM 切换时间 ta、tb、tc,来生成三个中间变量 Tcmp1、Tcmp2、Tcmp3,用于后续的 比较器(Comparator)触发 PWM 波形。
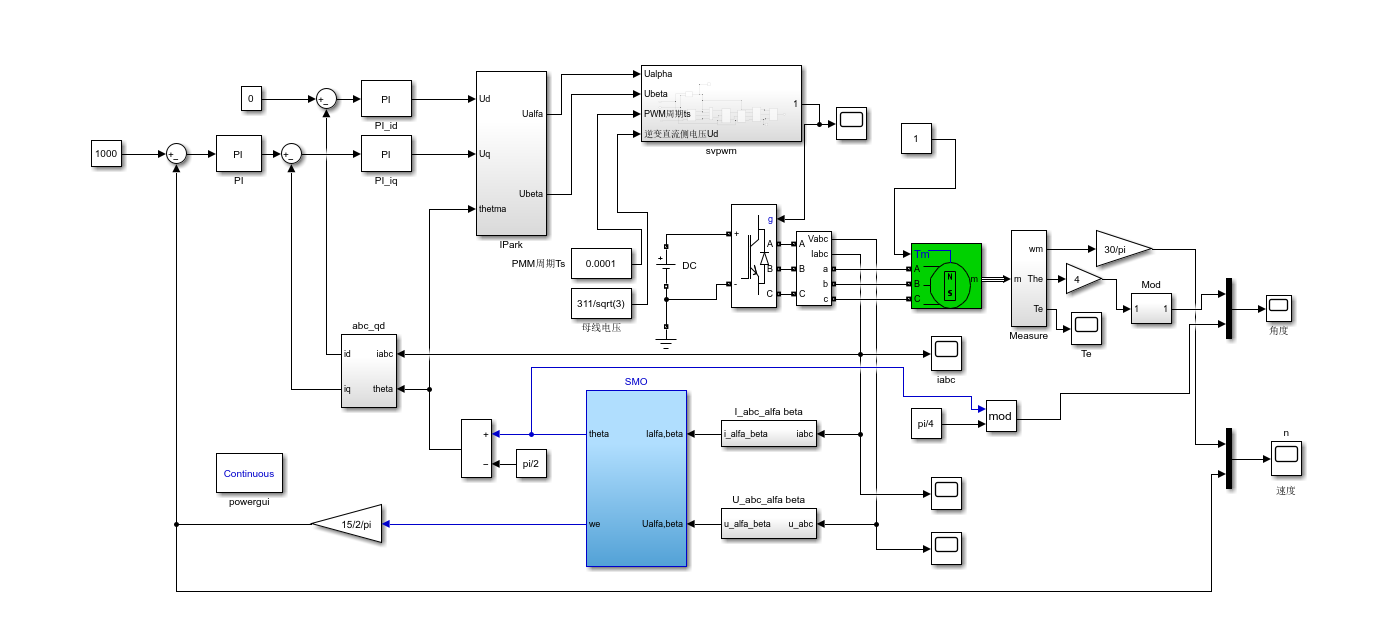
3.Park+Clarke
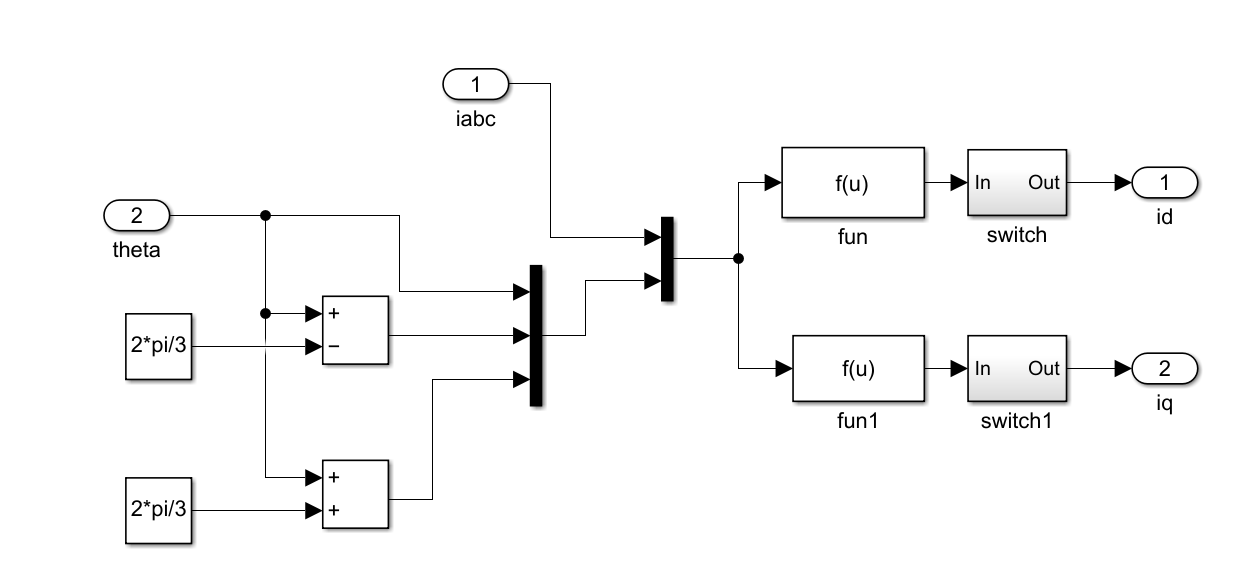
这是一个"三相电流到 dq 坐标系变换"的模块,即 Clarke 变换 + Park 变换的组合,用于电机控制中的矢量变换(坐标变换)
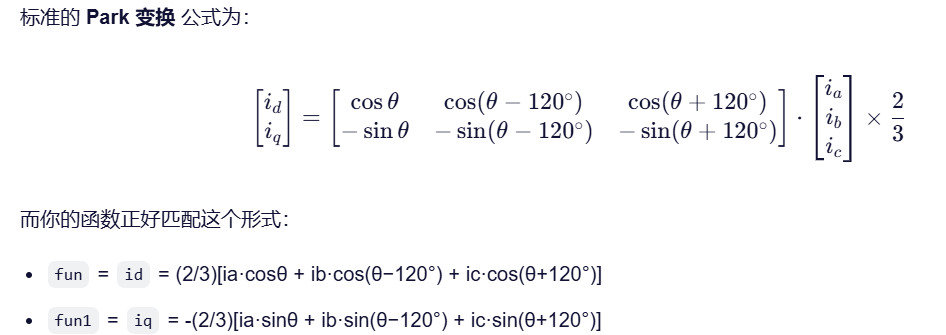
4.SMO
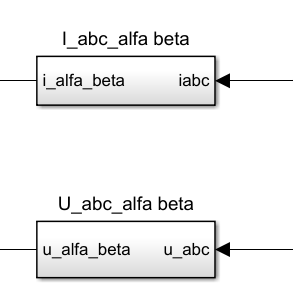
1.Iα,Iβ,Uα,Uβ
cpp
// ==================== 电流值更新 ====================
// 滑模观测器部分:如果没有检测到编码器反馈,则使用滑模观测器估计值
Angle_SMOPare.Ialpha = current_s.Ialfa; // 使用实际的α轴电流值
Angle_SMOPare.Ibeta = current_s.Ibeta; // 使用实际的β轴电流值
// ==================== 电压值转换 ====================
// 将PWM占空比电压转换为实际的电压值,d轴和q轴电压值需要转换
// 使用DCBUSVALUE(直流母线电压)和PWM_PERIOD(PWM周期),1.73205f是sqrt(3),用于将线电压转换为相电压
Angle_SMOPare.Valpha = (float)epwm_s.Ualfa * DCBUSVALUE / PWM_PERIOD / 1.73205f; // 转换为实际电压Valpha
Angle_SMOPare.Vbeta = (float)epwm_s.Ubeta * DCBUSVALUE / PWM_PERIOD / 1.73205f; // 转换为实际电压Vbeta实际中使用 Clarke计算出来的Iα,Iβ,Uα,Uβ作物观测器的输入。
2.反电动势计算
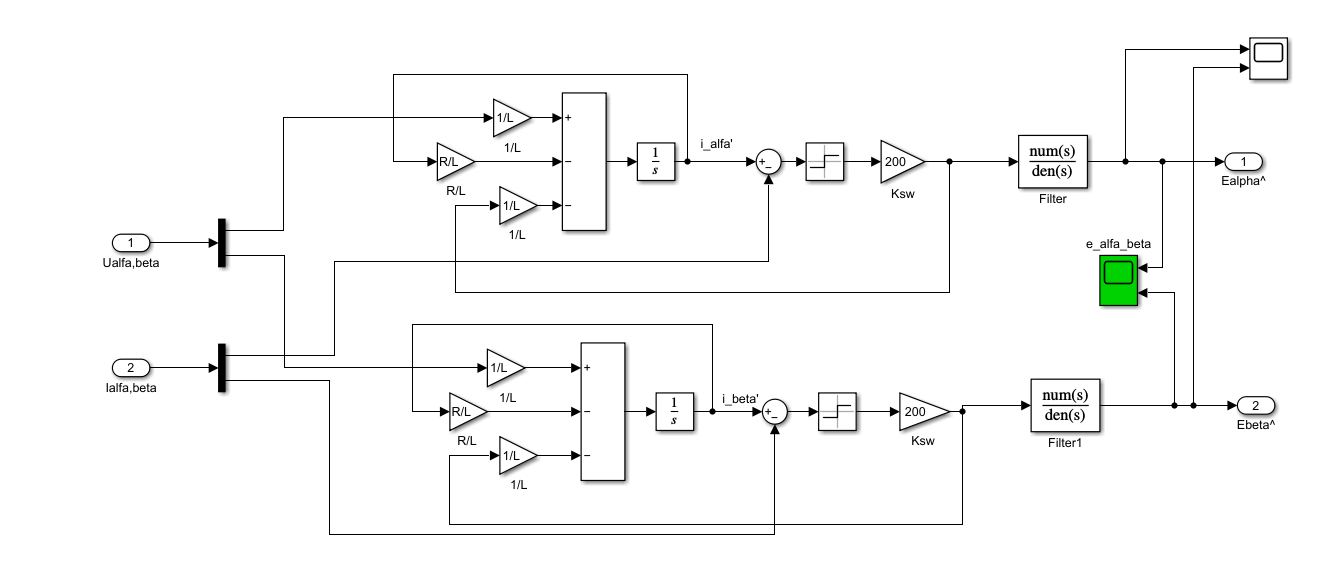
✅ 输入信号:
| 编号 | 名称 | 含义 |
|---|---|---|
| 1 | Ualfa_beta | αβ 坐标系下的定子电压(即 Uα, Uβ) |
| 2 | Ialfa_beta | αβ 坐标系下的定子电流(即 iα, iβ) |
⚠️ 注意:这些是经过 Clarke 变换后的两相静止坐标系量,单位为 V 和 A。
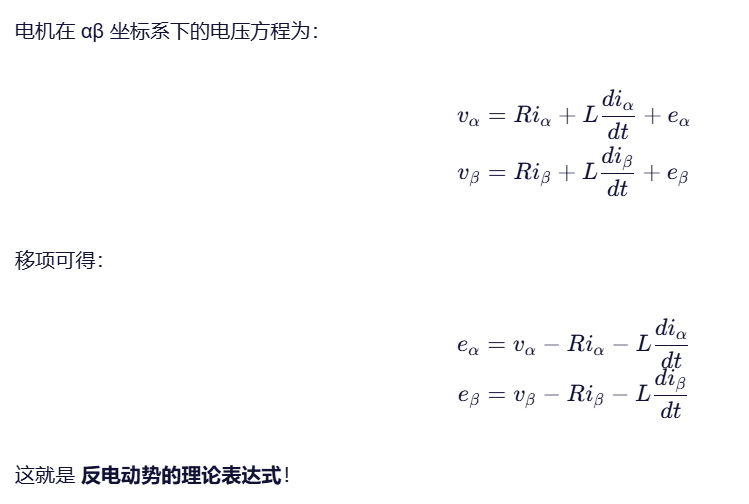
3.正反切