目录
[4.更新隐藏状态 h_t](#4.更新隐藏状态 h_t)
[5.计算输出 y_t](#5.计算输出 y_t)
[五、残差 + 输出投影](#五、残差 + 输出投影)
写在前面
接下来我们介绍Mamba的实现。首先需要厘清两个关键概念。S4(结构化状态空间序列模型) 作为一种经典的序列模型,其核心是通过一组固定不变的参数来捕捉序列中的长期依赖关系。而它的进化版本 S6(选择性状态空间模型),则突破性地让这些参数能够根据当前输入动态变化,从而实现了对关键信息的选择性关注。

Mamba的基本构建模块正是S6块。通俗地说,Mamba模型可以理解为多个S6模块的堆叠,并通过巧妙的硬件感知设计,高效地实现了这种选择性机制。接下来,我们将从代码层面解构Mamba是如何实现这一过程的。
值得注意的是我使用的代码不是mamba的官方代码(省略了depthwise conv、scan kernel等),而是根据公式的实现,这在效率方面会有一些欠缺,但是易于学习理解。
一、整体结构
我们以输入1, 16, 128为例,如果输入是一句话的话就是batch=1、16个token、token的向量维度128。
整体结构如下:
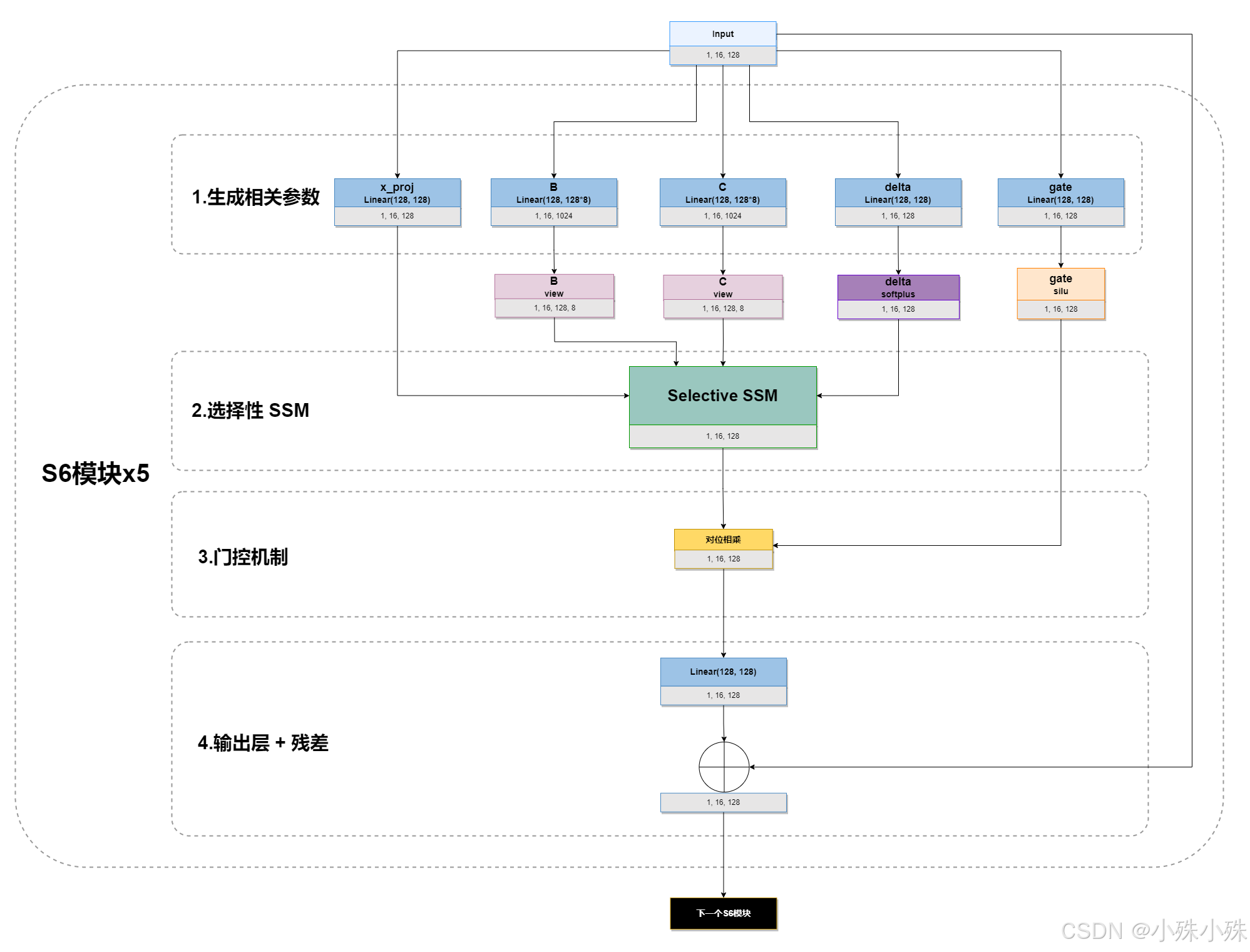
可以看到整个mamba有n个s6模块组成,当然这里n=5,每个s6又有如下模块。
二、生成输入相关参数
模型由输入动态生成 B、C、Δ、gate 参数。区别于普通 SSM(固定参数),Mamba 引入 selective 机制:
**B(x):**输入到状态的控制矩阵(控制输入如何影响状态);
**C(x):**状态到输出的观测矩阵(状态如何影响输出);
**Δ(x):**时间步长(步长可变,相当于动态决定事件间隔);
**gate(x):**门控信号(决定信息流量)
代码实现:
python
self.to_xproj = nn.Linear(dim, dim) # 线性投影后的输入 x_proj
self.to_B = nn.Linear(dim, dim * state_dim) # 每步生成输入映射矩阵 B
self.to_C = nn.Linear(dim, dim * state_dim) # 每步生成输出映射矩阵 C
self.to_delta = nn.Linear(dim, dim) # 每步生成时间步 Δ
self.to_gate = nn.Linear(dim, dim) # 每步生成门控系数 gate三、选择性状态空间模型离散化
这一步(Selective SSM)确定每个时间步的更新权重,是官方 Mamba 的核心数学步骤之一。
连续时间方程离散化得到:
展开得到:
其中变量的解释请看这里:Mamba的前世今生!
整体流程如下:
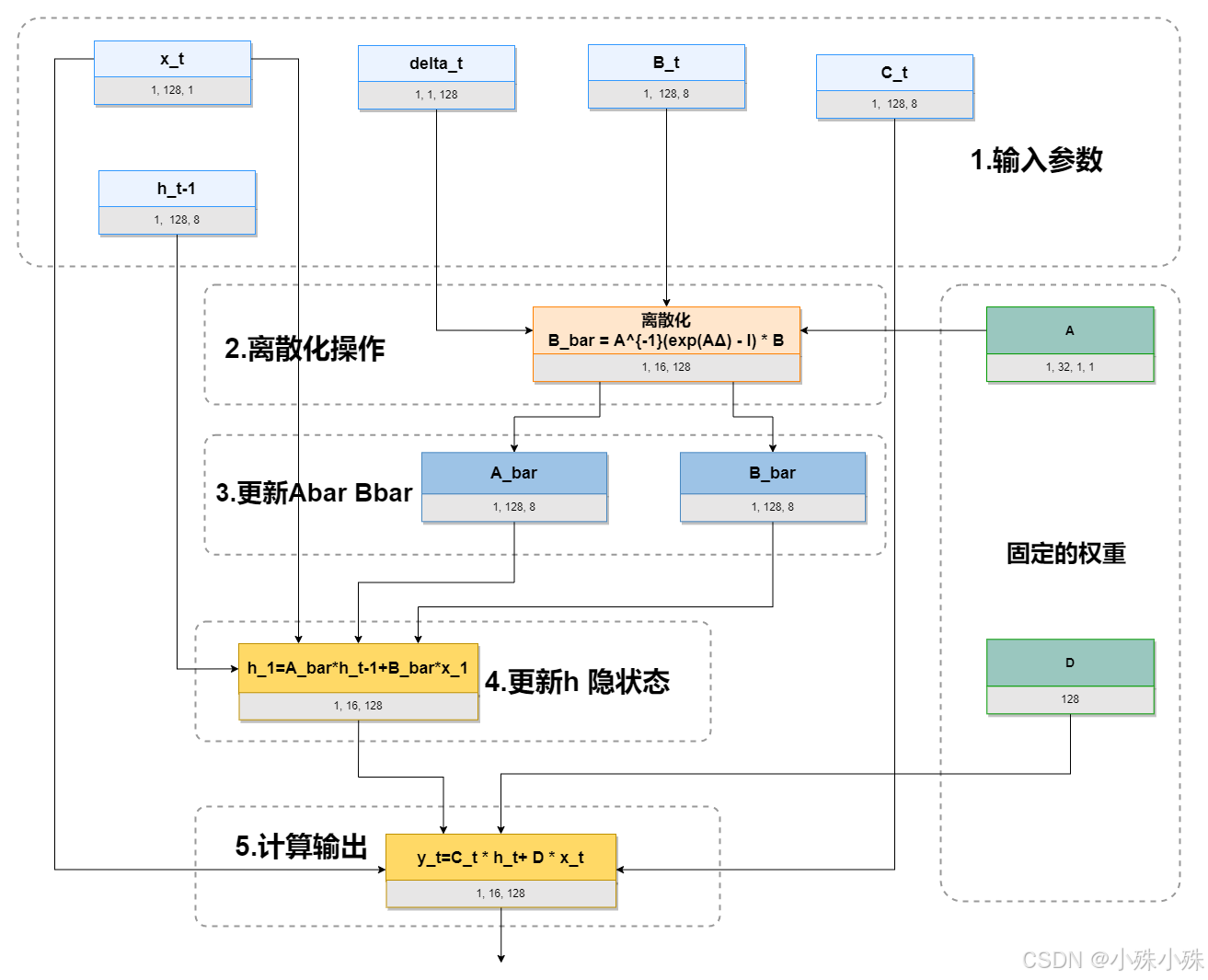
从上图可以看到Selective SSM的流程为:
1.输入参数
每个时间步 t 的输入参数包括:
:序列当前时间步的输入向量
:输入控制矩阵,由输入动态生成
:输出观测矩阵,由输入动态生成
:时间步长,由输入动态生成
:上一个时间步的隐藏状态
固定权重参数:
:状态矩阵,对角负值,用于控制状态自然衰减
:跳跃连接系数,用于直接把输入加入输出
每个参数在每个时间步可能不同(、
、
是动态生成的),这就是 Selective 的核心。
2.执行离散化操作
将连续时间状态空间模型离散化:
注意这里的下标 t 表示每个时间步的离散化操作,A 是固定矩阵,是动态生成的。
3.更新离散化矩阵
根据离散化公式,得到当前时间步 t 的,它们决定了状态 h 的更新方式。:
:状态衰减矩阵
:输入映射矩阵
4.更新隐藏状态 h_t
这是 SSM 信号处理的核心步骤。状态更新公式:
第一项表示旧状态的衰减与传递;第二项表示当前输入对状态的贡献。
5.计算输出 y_t
将进入门控和输出层进行进一步处理得到这个 。输出计算公式:
和
:将隐藏状态投影到输出空间
和
:直接输入跳跃到输出,形成残差
计算完的y_t会被送到下一循环用来计算,直到序列完成。
6.总结步骤
| 步骤 | 公式 | 含义 |
|---|---|---|
| 1. 输入参数 | x_t, B_t, C_t, Δ_t, h_{t-1}, A, D | 准备更新所需变量 |
| 2. 离散化 | Ā_t = exp(A Δ_t), B̄_t = A^{-1}(exp(A Δ_t) - I) B_t | 连续 → 离散 |
| 3. 更新离散矩阵 | Ā_t, B̄_t | 不同时间步不同参数 |
| 4. 更新状态 | h_t = Ā_t h_{t-1} + B̄_t x_t | 状态推进 |
| 5. 输出 | y_t = C_t h_t + D x_t | 得到当前时间步输出 |
下面是所有参数的含义:
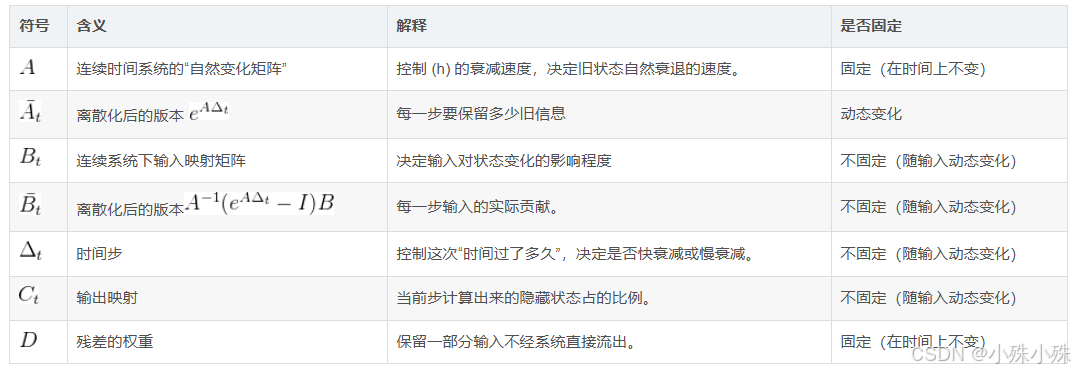
7.代码实现
python
def selective_ssm(self, x, B, C, delta):
"""
选择性 SSM 正向传播逻辑。
参数:
x : (B, L, D) 输入序列
B : (B, L, D, S) 输入投影矩阵
C : (B, L, D, S) 输出投影矩阵
delta : (B, L, D) 每步时间间隔 Δ_t(正数)
返回:
y : (B, L, D) 序列输出
"""
Bsz, L, D = x.shape
S = self.state_dim
# 确保维度匹配
assert B.shape == (Bsz, L, D, S)
assert C.shape == (Bsz, L, D, S)
assert delta.shape == (Bsz, L, D)
# 将 A 扩展为 (1, D, S) 以便广播
A_unsq = self.A.unsqueeze(0)
# 初始化隐藏状态 h_0 = 0
h = torch.zeros(Bsz, D, S, device=x.device, dtype=x.dtype)
outputs = []
# ---------------------------------------------------------------
# 循环处理每个时间步
# ---------------------------------------------------------------
for t in range(L):
delta_t = delta[:, t:t + 1, :] # (B, 1, D)
B_t = B[:, t] # (B, D, S)
# 计算离散化后的系数 B_bar, A_bar
B_bar, exp_a = self._compute_discrete_Bbar(A_unsq, delta_t, B_t)
A_bar = exp_a # (B, D, S)
# 状态更新方程:
# h_t = A_bar * h_{t-1} + B_bar * x_t
x_t = x[:, t].unsqueeze(-1) # (B, D, 1)
h = A_bar * h + B_bar * x_t # (B, D, S)
# 输出方程:
# y_t = sum(C_t * h_t, dim=-1) + D * x_t
C_t = C[:, t] # (B, D, S)
y_t = torch.sum(C_t * h, dim=-1) + self.D * x[:, t] # (B, D)
outputs.append(y_t)
# 堆叠输出成序列
y = torch.stack(outputs, dim=1) # (B, L, D)
return y四、门控(Gating)
为了增强表达能力,Mamba 在 SSM 输出后加入门控,门控网络产生可学习的 mask,控制不同特征维度的信息流通。
不是每个状态向量或每个通道的输出都需要直接传给下一层或输出。门控机制提供一个动态权重(0~1 或经过非线性函数)来控制哪些信息被保留,哪些被抑制。
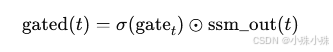
代码实现:
python
gated = F.silu(gate) * ssm_out五、残差 + 输出投影
残差 + 输出投影是 深度神经网络稳定训练的关键,尤其是堆叠多层 S6 时。防止梯度消失/梯度爆炸,同时每个输出通道可以利用所有输入通道的信息。
如果是S6的堆叠,那输出还会输入到下一个S6,一直循环下去直到完成所有的循环。
代码实现:
python
out = self.out_proj(gated) # 输出线性投影,通道混合
out = out + residual # 残差连接,稳定训练六、总结
最后简单总结一下整个过程:
1.利用线性投影准备需要的数据;
2.Selective SSM:根据公式更新
,期间
都会更新;根据公式
更新输出,期间
会更新;
3.计算门控gate,控制哪些信息被保留,哪些被抑制;
4.残差 + 输出投影:增强训练的稳定性,同时每个输出通道可以利用所有输入通道的信息。
再看一下全部代码:
python
import torch
import torch.nn as nn
import torch.nn.functional as F
class MambaBlock(nn.Module):
"""
✅ Mamba 的选择性状态空间模型(Selective SSM)实现。
---------------------------------------------------------------------
数学形式(连续时间):
dh/dt = A h + B x
y = C h + D x
离散化(解析解):
h_t = exp(AΔ) h_{t-1} + (A^{-1}(exp(AΔ) - I)) B x_t
y_t = C h_t + D x_t
特点:
- A 是对角的(逐元素),因此可以向量化计算。
- Δ(delta)是每个时间步、每个特征动态生成的。
- B 和 C 也是每个时间步动态生成(selective)。
- 包含 depthwise 卷积以捕捉局部特征。
- 包含门控机制 (gate) 与残差连接。
注意:
该版本使用 Python 循环来扫描序列(L 次循环),
虽然比 CUDA kernel 慢,但逻辑上完全等价于官方 Mamba。
"""
def __init__(self, dim, state_dim=16, conv_size=4, eps=1e-6):
"""
Args:
dim: 输入特征维度 (D)
state_dim: 状态空间维度 (S)
conv_size: depthwise 卷积核大小
eps: 数值稳定的阈值,用于避免除零
"""
super().__init__()
self.dim = dim
self.state_dim = state_dim
self.eps = eps # 防止除以 0 的小常数
# ------------------------------------------------------------------
# 各种投影层,用于生成输入相关参数
# 我们不用一个大线性层切片,而是分开写,避免索引错乱
# ------------------------------------------------------------------
self.to_xproj = nn.Linear(dim, dim) # 线性投影后的输入 x_proj
self.to_B = nn.Linear(dim, dim * state_dim) # 每步生成输入映射矩阵 B
self.to_C = nn.Linear(dim, dim * state_dim) # 每步生成输出映射矩阵 C
self.to_delta = nn.Linear(dim, dim) # 每步生成时间步 Δ
self.to_gate = nn.Linear(dim, dim) # 每步生成门控系数 gate
# ------------------------------------------------------------------
# 状态矩阵 A
# 每个通道(dim)有 state_dim 个隐藏状态。
# 初始化为负值,代表指数衰减(系统稳定)
# ------------------------------------------------------------------
self.A = nn.Parameter(-torch.abs(torch.randn(dim, state_dim)) * 1.0)
# 跳跃连接系数 D(相当于残差比例)
self.D = nn.Parameter(torch.ones(dim))
# 输出线性层
self.out_proj = nn.Linear(dim, dim)
# 层归一化
self.norm = nn.LayerNorm(dim)
# ======================================================================
# 计算离散化后的 B_bar 和 A_bar(exp(AΔ))
# ======================================================================
def _compute_discrete_Bbar(self, A_unsq, delta_t, B_t):
"""
计算:
B_bar = A^{-1}(exp(AΔ) - I) * B
同时返回 A_bar = exp(AΔ)
参数:
A_unsq : (1, D, S) 模型的状态矩阵参数 A(广播形状)
delta_t : (B, 1, D) 当前时间步 Δ_t
B_t : (B, D, S) 当前时间步的输入映射 B_t
返回:
B_bar : (B, D, S)
exp_a : (B, D, S) 即 A_bar = exp(AΔ)
"""
# 扩展 Δ_t 形状 (B, D, 1)
delta_bds = delta_t.squeeze(1).unsqueeze(-1)
# 计算 A * Δ (逐元素)
a = A_unsq * delta_bds # (B, D, S)
# 指数项 exp(AΔ)
exp_a = torch.exp(a)
# 计算分子 (exp(AΔ) - I)
numerator = exp_a - 1.0
# 防止除零:当 |A| 很小的时候使用级数展开近似
A_bds = A_unsq # (1, D, S)
small_mask = A_bds.abs() <= self.eps # (1, D, S)
# 默认计算 (exp(AΔ)-1)/A
ratio = numerator / A_bds
# 近似展开式:当 A ≈ 0 时,(exp(AΔ)-1)/A ≈ Δ + 0.5 * A * Δ^2
if small_mask.any():
series_approx = delta_bds + 0.5 * (A_bds * (delta_bds ** 2))
mask_exp = small_mask.expand_as(ratio)
ratio = torch.where(mask_exp, series_approx.expand_as(ratio), ratio)
# 得到离散化后的 B_bar
B_bar = ratio * B_t
return B_bar, exp_a
# ======================================================================
# 选择性状态空间前向传播
# ======================================================================
def selective_ssm(self, x, B, C, delta):
"""
选择性 SSM 正向传播逻辑。
参数:
x : (B, L, D) 输入序列
B : (B, L, D, S) 输入投影矩阵
C : (B, L, D, S) 输出投影矩阵
delta : (B, L, D) 每步时间间隔 Δ_t(正数)
返回:
y : (B, L, D) 序列输出
"""
Bsz, L, D = x.shape
S = self.state_dim
# 确保维度匹配
assert B.shape == (Bsz, L, D, S)
assert C.shape == (Bsz, L, D, S)
assert delta.shape == (Bsz, L, D)
# 将 A 扩展为 (1, D, S) 以便广播
A_unsq = self.A.unsqueeze(0)
# 初始化隐藏状态 h_0 = 0
h = torch.zeros(Bsz, D, S, device=x.device, dtype=x.dtype)
outputs = []
# ---------------------------------------------------------------
# 循环处理每个时间步
# ---------------------------------------------------------------
for t in range(L):
delta_t = delta[:, t:t + 1, :] # (B, 1, D)
B_t = B[:, t] # (B, D, S)
# 计算离散化后的系数 B_bar, A_bar
B_bar, exp_a = self._compute_discrete_Bbar(A_unsq, delta_t, B_t)
A_bar = exp_a # (B, D, S)
# 状态更新方程:
# h_t = A_bar * h_{t-1} + B_bar * x_t
x_t = x[:, t].unsqueeze(-1) # (B, D, 1)
h = A_bar * h + B_bar * x_t # (B, D, S)
# 输出方程:
# y_t = sum(C_t * h_t, dim=-1) + D * x_t
C_t = C[:, t] # (B, D, S)
y_t = torch.sum(C_t * h, dim=-1) + self.D * x[:, t] # (B, D)
outputs.append(y_t)
# 堆叠输出成序列
y = torch.stack(outputs, dim=1) # (B, L, D)
return y
# ======================================================================
# 前向传播
# ======================================================================
def forward(self, x):
"""
前向传播逻辑。
参数:
x: (B, L, D)
返回:
out: (B, L, D)
"""
Bsz, L, D = x.shape
residual = x # 残差连接
x_norm = self.norm(x) # 层归一化,稳定训练
# ------------------ 生成各个参数 ------------------
x_proj = self.to_xproj(x_norm) # (B, L, D)
B_flat = self.to_B(x_norm) # (B, L, D*S)
C_flat = self.to_C(x_norm) # (B, L, D*S)
delta = self.to_delta(x_norm) # (B, L, D)
gate = self.to_gate(x_norm) # (B, L, D)
# 调整 B、C 形状
B = B_flat.view(Bsz, L, D, self.state_dim)
C = C_flat.view(Bsz, L, D, self.state_dim)
# ------------------ delta 保证正值 ------------------
delta = F.softplus(delta)
# ------------------ 选择性 SSM ------------------
ssm_out = self.selective_ssm(x_proj, B, C, delta) # (B, L, D)
# ------------------ 门控机制 ------------------
gated = F.silu(gate) * ssm_out # element-wise gate
# ------------------ 输出层 + 残差 ------------------
out = self.out_proj(gated)
out = out + residual
return out
# ======================================================================
# ✅ 测试函数
# ======================================================================
def test_mamba():
"""
测试 Mamba 模块的输入输出形状和梯度流。
"""
torch.manual_seed(0)
model = MambaBlock(dim=128, state_dim=8)
x = torch.randn(1, 16, 128)
y = model(x)
print("✅ 输出 shape:", y.shape) # 期望 (2, 16, 128)
# 反向传播测试,确保参数都参与计算图
(y.sum()).backward()
n_grad = sum(1 for p in model.parameters() if p.grad is not None)
print(f"✅ 有 {n_grad} 个参数成功参与梯度计算")
if __name__ == "__main__":
test_mamba()Mamba实现就介绍到这!
关注不迷路(*^▽^*),暴富入口==》 https://bbs.csdn.net/topics/619691583