【剑斩OFFER】算法的暴力美学——除自身以外数组的乘积

一、题目描述

二、算法原理

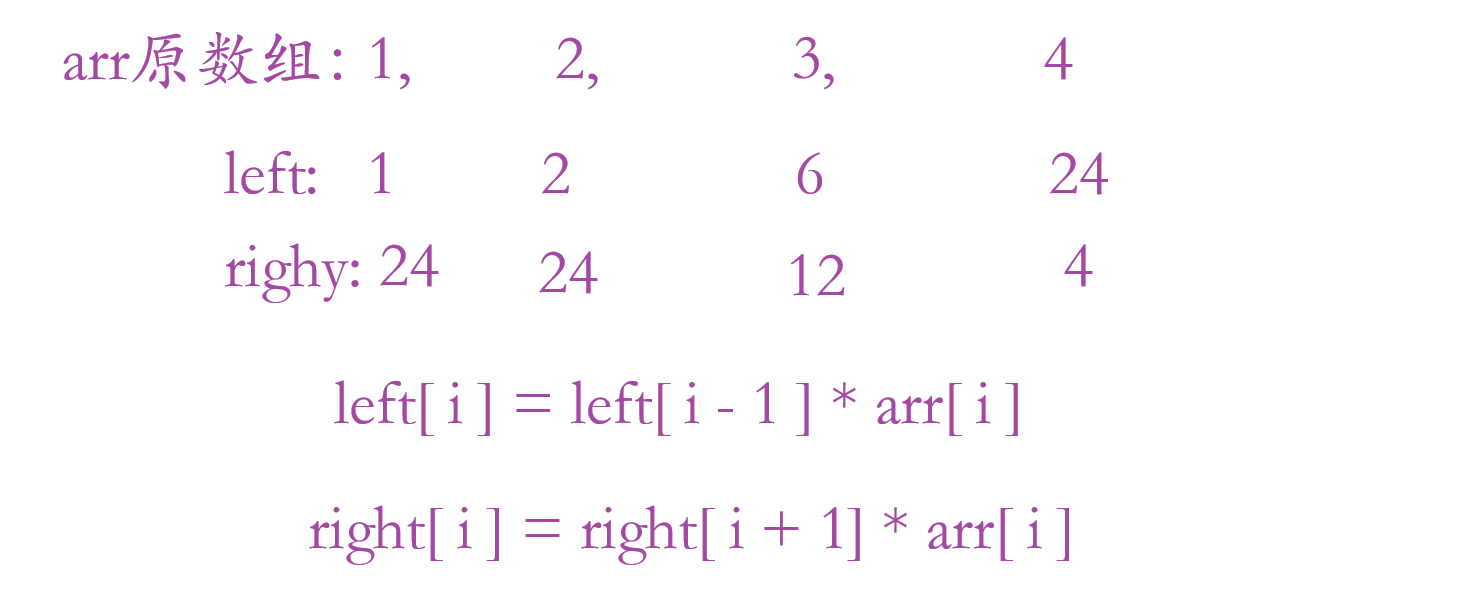
我们如果暴力查找时复杂度是非常高的，所以这里我们弄两个数组，一个求的是前缀的积，另外一个求的是后缀的积。

求前缀的时候是从左往右求，而后缀是从右往左求。

前缀特殊情况：当 i = 0 时，i - 1 是会越界的，所以这里当 i = 0 时，直接让他等于原数组的第一个数字就行。

后缀特殊情况：当 i = 数组长度 - 1，i + 1 是会越界的，所以当 i = 数组长度 - 1 时，直接等于原数组的最后一个数。

上面图片的 left 就是前缀求积，而 right 就是求后缀的积。

那么怎么使用这俩个数组来解决这道题目呢？

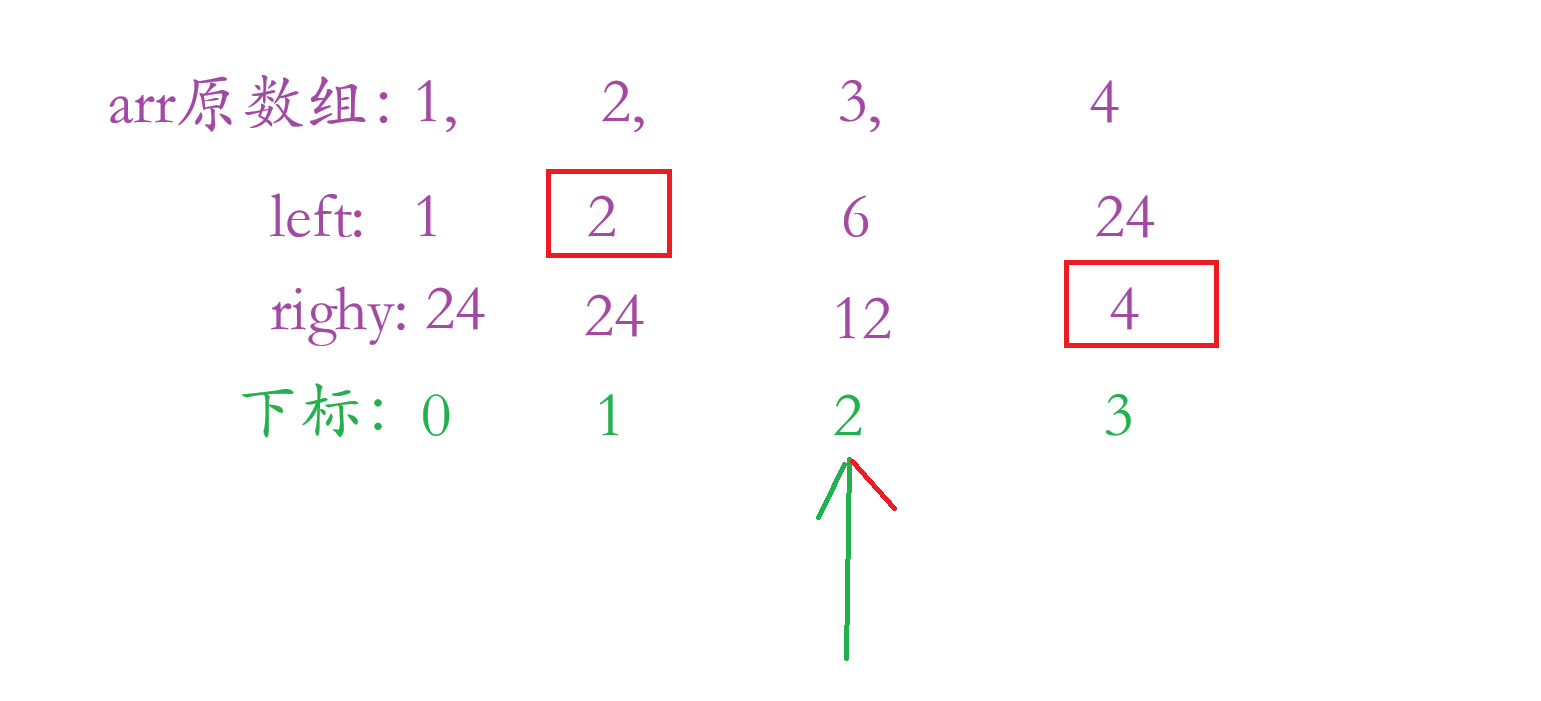
当 i = 2 ，这里就等于：2 * 4 = 8；

所以：这里也就得出个公式：ret i = left i - 1 * right i + 1

这个公式有两个特殊情况：

当 i = 0，i - 1 会越界，所以当 i = 0，直接让他等于：right i + 1

当 i = 数组的长度 - 1，i + 1会越界，所以直接让他等于：left i - 1

三、代码实现

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        vector<int> left(nums.size());
        vector<int> right(nums.size());
        int len = nums.size();
        for(int i = 0; i < len; i++)
        {
            if(i == 0) left[i] = nums[i];
            else left[i] = left[ i - 1] * nums[i];
        }
        for(int j = len - 1; j >= 0; j--)
        {
            if(j == len - 1) right[j] = nums[j];
            else right[j] = right[j + 1] * nums[j];
        }

        vector<int> ret(len);

        for(int k = 0; k < len; k ++)
        {
            if(k == 0) ret[k] = right[k + 1];
            else if(k == len - 1) ret[k] = left[k - 1];
            else ret[k] = left[k - 1] * right[k + 1];
        }
        return ret;
    }
};