R语言机器学习系列|随机森林模型特征重要性排序的R语言实现

2301_783360132025-11-18 21:31

原文 ：R语言机器学习系列|随机森林模型特征重要性排序的R语言实现

目录

)

1. 名词解释

1.1 基尼不纯度（Gini impurity）或信息熵（information entropy）

好的，这是一个非常核心的机器学习概念，尤其在决策树算法中。我会用清晰易懂的方式解释它们。

简单来说，基尼不纯度和信息熵都是用来衡量一个数据集合"混乱程度"的指标。它们帮助决策树决定如何最佳地分割数据。

想象你在整理一堆混在一起的乒乓球（红色和蓝色），你的目标是把它们按颜色分开。

1. 信息熵 (Information Entropy)

核心思想： 熵源于信息论，表示"信息的不确定性"或"预期的信息量"。一个集合越混乱、越不可预测，它的熵就越高。

  • 熵高（接近1.0）： 集合中各种类别比例相当（比如50%红球，50%蓝球）。你完全无法确定随手摸一个球是什么颜色，不确定性极高。
  • 熵低（接近0）： 集合中几乎只有一种类别（比如99%红球，1%蓝球）。你几乎可以确定摸到的是红球，不确定性极低。

计算公式：

对于一个有两个类别（0和1）的数据集，公式为：
Entropy = -p(0) * log₂(p(0)) - p(1) * log₂(p(1))

其中 p(0) 和 p(1) 分别是类别0和类别1在集合中的比例。

直观理解：

  • 如果集合全是红球（p(红)=1， p(蓝)=0）：
    Entropy = -1 * log₂(1) - 0 * log₂(0) = 0 （完全纯净，没有不确定性）
  • 如果红蓝球各占一半（p(红)=0.5， p(蓝)=0.5）：
    Entropy = -0.5 * log₂(0.5) - 0.5 * log₂(0.5) = 1 （极度混乱，不确定性最大）

单位： 比特，因为它源于信息论。

2. 基尼不纯度 (Gini Impurity)

核心思想： 基尼不纯度直接衡量"从集合中随机抽取两个样本，它们属于不同类别的概率"。

  • 基尼不纯度高（接近0.5）： 随机抽两个球，它们颜色不同的概率很高，说明集合很混乱。
  • 基尼不纯度低（接近0）： 随机抽两个球，它们颜色几乎总是相同，说明集合很纯净。

计算公式：

同样对于两个类别的数据集：
Gini = 1 - [p(0)² + p(1)²]

直观理解：

  • 如果集合全是红球（p(红)=1， p(蓝)=0）：
    Gini = 1 - (1² + 0²) = 0 （抽到的两个球肯定同色，纯净度最高）
  • 如果红蓝球各占一半（p(红)=0.5， p(蓝)=0.5）：
    Gini = 1 - (0.5² + 0.5²) = 1 - (0.25 + 0.25) = 0.5 （抽到的两个球颜色不同的概率是50%，混乱度最高）

在决策树中如何工作？

决策树（如CART, C4.5, ID3）的目标是创建"纯净"的子节点。在决定如何分割一个节点时，它会评估所有可能的分割方式，并选择那个能最大程度降低子节点不纯度的分割方式。

这个"不纯度的降低量"被称为 信息增益。

信息增益 = 父节点的不纯度 - (加权平均的)子节点们的不纯度

决策树算法会选择那个能带来最大信息增益的分割点。

举个例子：

一个节点有5个红球和5个蓝球。

  • 父节点的基尼不纯度 = 0.5

  • 你尝试按特征A分割：

    • 左子节点：4个红球，1个蓝球 -> 基尼 ≈ 0.32
    • 右子节点：1个红球，4个蓝球 -> 基尼 ≈ 0.32
    • 加权平均基尼 = (5/10)*0.32 + (5/10)*0.32 = 0.32
    • 信息增益 = 0.5 - 0.32 = 0.18

  • 你尝试按特征B分割：

    • 左子节点：3个红球，3个蓝球 -> 基尼 = 0.5
    • 右子节点：2个红球，2个蓝球 -> 基尼 = 0.5
    • 加权平均基尼 = 0.5
    • 信息增益 = 0.5 - 0.5 = 0

显然，按特征A分割更好，因为它带来了更高的信息增益（0.18），使子节点变得更纯净。

基尼不纯度 vs. 信息熵：如何选择？

特性 基尼不纯度 (Gini Impurity) 信息熵 (Information Entropy)
计算 计算更快（因为没有对数运算）。 计算稍慢（涉及对数计算）。
度量角度 从"分类错误"的概率出发。 从"信息不确定性"出发。
曲线形状 在计算纯度时，对类别比例的变化不那么敏感。 对类别比例的变化更敏感。
结果 倾向于从数据集中隔离出最常见的类别。 倾向于产生更平衡的树。
实际应用 CART算法 的默认选择（如Scikit-learn中的DecisionTreeClassifier）。 ID3, C4.5算法使用。

总结与建议：

  1. 本质相同：它们的目标和效果非常相似，都是在衡量数据集的混乱程度，以指导决策树进行最优分割。
  2. 性能差异微小：在实践中，选择基尼不纯度还是信息熵通常不会对最终模型的准确性产生巨大影响。
  3. 默认选择 ：由于计算效率 的优势，很多库（如Scikit-learn）默认使用基尼不纯度。这通常是一个安全且高效的选择。
  4. 都可以尝试：你可以把它们都试一下，看看哪个在你的特定数据集上表现稍好，但通常差异不大。

可以把它们理解为两种不同的"尺子"，一把是厘米尺（基尼），一把是英寸尺（熵），它们都能测量长度（不纯度），只是单位和刻度略有不同，但最终都能帮你找到最好的分割点。

1.2 特征重要性是什么，如何计算特征重要性

好的，这是一个关于机器学习模型可解释性非常重要的问题。我会详细解释特征重要性是什么，以及它是如何计算的。

什么是特征重要性？

特征重要性 是一个指标，用于衡量数据集中每个特征（变量）对于构建一个预测模型（尤其是树模型）的贡献程度。它回答了这个问题："在模型做决策时，哪个特征最重要？"

核心思想： 一个特征越频繁地被用来分割数据，并且它带来的不纯度下降（信息增益） 越大，那么这个特征就越重要。

为什么需要特征重要性？

  1. 模型可解释性： 理解模型是如何工作的，哪些因素驱动了预测。
  2. 特征工程： 识别并移除不重要的特征，简化模型，防止过拟合，加快训练速度。
  3. 业务洞察： 告诉业务方哪些因素是关键驱动因素。例如，在预测客户流失时，发现"客服通话时长"比"用户年龄"重要得多，这可以直接指导业务行动。

如何计算特征重要性？（以决策树/随机森林为例）

计算过程主要分为两步，这正是您提到的"加权平均"思想的体现。

第一步：为每个节点计算特征的重要性（不纯度下降）

每当决策树在一个节点上使用某个特征 F 进行分割时，都会计算一次该特征带来的"不纯度下降"。这个值就是我们在上一个问题中提到的 信息增益。

计算公式：
ΔI = I_parent - (w_left * I_left + w_right * I_right)

其中：

  • I_parent：父节点的不纯度（基尼或熵）。
  • I_left, I_right：分割后左右子节点的不纯度。
  • w_left, w_right：分别是左右子节点样本数占父节点样本数的比例。

这个 ΔI 就是这个节点上，特征 F 的"贡献分数"。

第二步：在整个模型范围内汇总特征的重要性

现在，我们需要把所有树、所有节点上，关于同一个特征 F 的贡献分数汇总起来。这里有 两种主要的平均方式：

1. 加权平均（更常用，更合理）

这是Scikit-learn等主流库中默认使用的方法。

计算方法：

  1. 对于特征 F，找到所有使用它进行分割的节点。
  2. 将所有这些节点的 ΔI（不纯度下降）相加。
  3. 同时，将所有这些节点的加权样本数（即该节点分割时影响的样本数量）也考虑进去。

公式可以理解为：
Importance(F) = (所有使用F的节点的 ΔI 之和) / (所有节点的 ΔI 之和)

为什么是"加权"的？

因为一个节点包含的样本越多，这个节点上的决策就越重要，因此在这个节点上使用的特征 F 的贡献（ΔI）也就越重要。这个加权过程通过 ΔI 本身已经隐含了（因为 ΔI 的计算中包含了 w_left 和 w_right），并且在最后归一化时也考虑了总影响。

举个例子（随机森林）：

  • 假设我们有3棵树。
  • 特征 年龄 在第1棵树的一个节点（有1000个样本）上带来了很大的不纯度下降（比如 ΔI=0.1）。
  • 在第2棵树的两个节点（分别有500和300个样本）上带来了中等的不纯度下降（ΔI=0.05 和 0.03）。
  • 在第3棵树中没有被使用。
  • 那么特征 年龄 的重要性就是这三处贡献的加权总和：0.1 + 0.05 + 0.03 = 0.18。
  • 最后，将所有特征的重要性归一化 ，使其总和为1。如果所有特征的总重要性是1.8，那么 年龄 的最终重要性就是 0.18 / 1.8 = 0.1（即10%）。
2. 简单平均

这种方法较少使用，因为它忽略了节点样本数量的权重信息。

计算方法：

  1. 在每棵树中，计算每个特征的重要性（通过加权平均）。
  2. 然后，简单地计算这个特征在所有树中的重要性的平均值。

Importance(F) = (树1中F的重要性 + 树2中F的重要性 + ... + 树N中F的重要性) / N

缺点： 它平等地看待每一棵树，即使某棵树因为样本权重或结构的原因可能不如其他树可靠。

可视化与总结

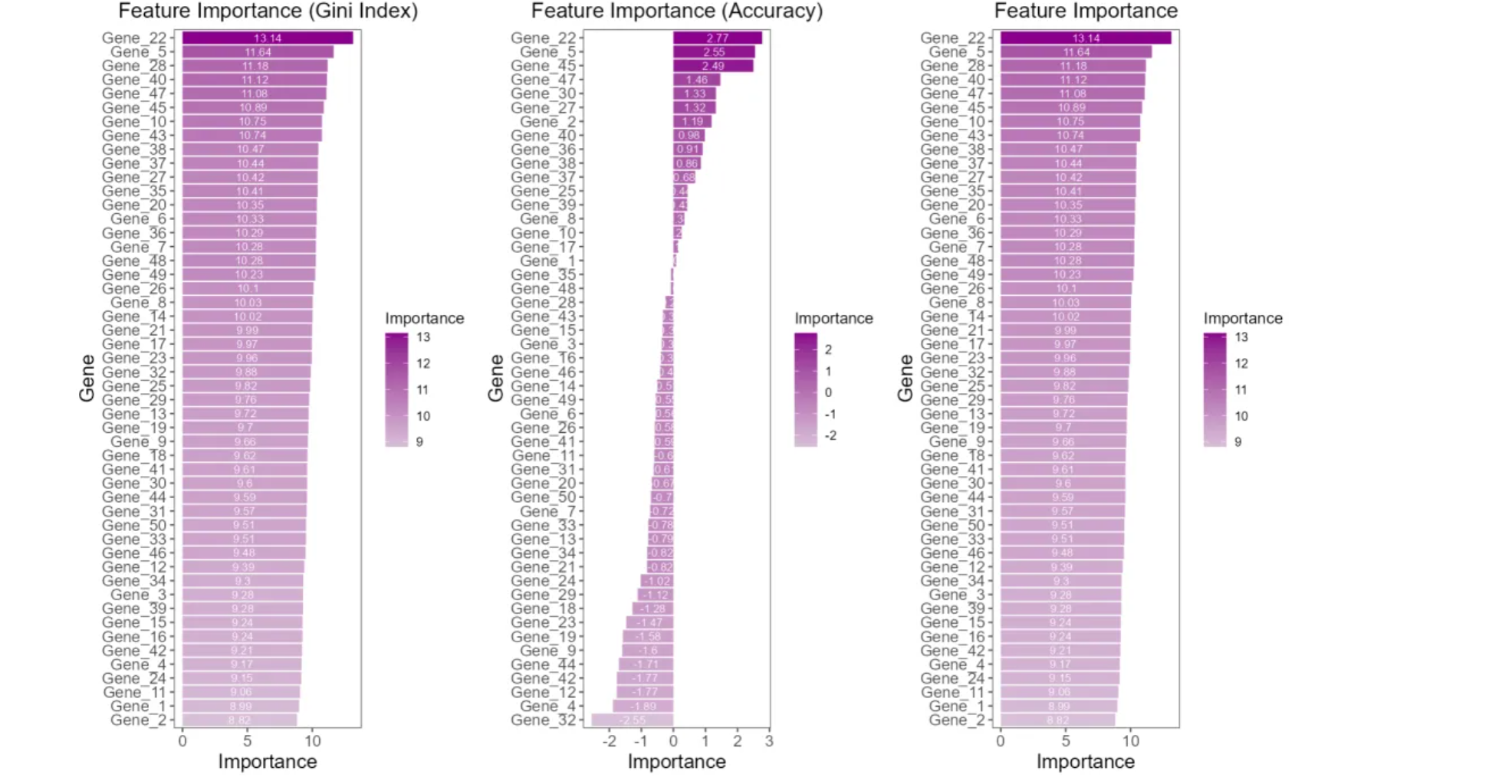
最终，你会得到一个类似这样的列表或图表：

特征重要性排序：

  1. 账户余额： 0.35 (35%)
  2. 交易次数： 0.25 (25%)
  3. 信用分数： 0.20 (20%)
  4. 年龄： 0.10 (10%)
  5. 地区： 0.10 (10%)

这清晰地告诉你，在预测（比如）客户是否会购买产品时，"账户余额"是最重要的决定性因素。

其他模型的特征重要性

  • 线性模型（如逻辑回归、线性回归）： 特征重要性通常由系数的绝对值来衡量。但在比较前，必须确保所有特征都已标准化（具有相同的尺度）。
  • 梯度提升树（如XGBoost, LightGBM）： 计算方法与随机森林类似，也是基于特征被用于分割时带来的信息增益（或类似的增益，如XGBoost的gain）的加权平均。
  • 排列重要性： 这是一种模型无关的方法。其原理是：随机打乱某个特征的数据，然后观察模型性能下降的程度。性能下降得越多，说明这个特征越重要。

关键要点

  1. 核心思想： 特征重要性基于特征在模型中带来的不纯度下降。
  2. 计算过程： 先计算每个节点上的贡献，再在整个模型（或森林）中按加权平均的方式汇总。
  3. 结果： 得到每个特征的相对重要性分数，通常归一化为百分比。
  4. 用途： 用于模型解释、特征选择和业务洞察。

1.3 两段关于特征重要性计算方法的描述。

分类问题中的特征重要性

原文：

"对于分类任务，特征重要性可以通过以下方式计算：对于每个决策树，计算特征在所有分裂节点中导致的平均不纯度减少。然后，将所有树中同一特征的平均值作为该特征的重要性得分。"

逐句解释：

  1. "对于每个决策树"

    • 这意味着我们是在集成学习方法（如随机森林）的背景下讨论的。随机森林由多棵决策树组成。

  2. "计算特征在所有分裂节点中导致的平均不纯度减少"

    • "不纯度减少" ：这就是我们之前讨论的信息增益。当决策树在一个节点上使用某个特征进行分割时，它会降低子节点的不纯度（基尼不纯度或信息熵）。
    • "在所有分裂节点中"：对于一棵树中的某个特征，我们找到所有使用该特征进行分割的节点。
    • "平均"：我们计算这些节点上不纯度减少的平均值。

    具体计算：

    • 对于特征F，在树T中：
      • 找到所有使用F分割的节点：节点₁, 节点₂, ..., 节点ₖ
      • 计算每个节点上的不纯度减少：ΔI₁, ΔI₂, ..., ΔIₖ
      • 计算平均值：平均不纯度减少 = (ΔI₁ + ΔI₂ + ... + ΔIₖ) / k

  3. "将所有树中同一特征的平均值作为该特征的重要性得分"

    • 现在我们扩展到整个森林（多棵树）：
      • 树₁中特征F的平均不纯度减少：Score₁
      • 树₂中特征F的平均不纯度减少：Score₂
      • ...
      • 树ₙ中特征F的平均不纯度减少：Scoreₙ
    • 最终特征F的重要性 = (Score₁ + Score₂ + ... + Scoreₙ) / n

直观理解：

在分类问题中，我们关心的是特征如何帮助我们更好地区分不同类别。一个特征如果在多棵树中都能有效地"净化"节点（让节点中的样本更倾向于属于同一类别），那么它就是重要的。

回归问题中的特征重要性

原文：

"对于回归任务，特征重要性可以通过计算特征在所有分裂节点中导致的平均误差减少来评估。这意味着，对于每个决策树，计算特征在所有分裂节点中对预测误差的贡献，然后将所有树中同一特征的平均值作为该特征的重要性得分。"

逐句解释：

  1. "计算特征在所有分裂节点中导致的平均误差减少"

    • 关键区别：这里用"误差减少"替代了"不纯度减少"。
    • 在回归问题中，我们预测的是连续值，所以不纯度指标不适用。
    • "误差" 通常指均方误差 或平均绝对误差。
    • "误差减少"：当一个节点被分割后，子节点的预测误差比父节点降低的程度。

    具体计算：

    • 父节点的MSE（均方误差）：MSE_parent
    • 分割后左子节点的MSE：MSE_left，右子节点的MSE：MSE_right
    • 误差减少 = MSE_parent - (w_left × MSE_left + w_right × MSE_right)
      • 其中w_left和w_right是左右子节点的样本权重

  2. "对于每个决策树，计算特征在所有分裂节点中对预测误差的贡献"

    • 与分类问题类似，对于一棵树中的某个特征：
      • 找到所有使用该特征分割的节点
      • 计算每个节点上的误差减少
      • 取平均值

  3. "将所有树中同一特征的平均值作为该特征的重要性得分"

    • 同样的集成思想：将同一特征在所有树中的得分取平均。

直观理解：

在回归问题中，我们关心的是特征如何帮助我们更准确地预测数值。一个特征如果在多棵树中都能有效地降低预测误差（让预测值更接近真实值），那么它就是重要的。

总结对比

方面 分类问题 回归问题
核心指标 不纯度减少（信息增益） 误差减少
具体度量 基尼不纯度或信息熵的降低 均方误差或平均绝对误差的降低
目标 让节点内的样本属于同一类别 让节点内的样本有相似的目标值
计算方法 1. 单棵树：特征在所有分裂节点中的平均不纯度减少 2. 整个森林：所有树中该特征得分的平均值 1. 单棵树：特征在所有分裂节点中的平均误差减少 2. 整个森林：所有树中该特征得分的平均值

重要说明：

您描述的这种方法（简单平均）是特征重要性计算的一种方式。在实际应用中（如Scikit-learn），更常用的是加权平均方法，它会考虑每个节点影响的样本数量，这样影响更多样本的节点会获得更高的权重。

无论采用哪种平均方式，核心思想是一致的：特征的重要性取决于它帮助模型做出更好决策的能力------在分类中是更好地区分类别，在回归中是更准确地预测数值。

1.4 袋外误差（OOB Error）: 随机森林内置的交叉验证，无需额外分割数据"交叉验证是什么，为什么无需额外分割数据

好的，这是一个非常关键的概念，能体现出随机森林算法的巧妙之处。我们来详细拆解一下。

第一部分：什么是交叉验证？

核心思想： 交叉验证是一种评估模型泛化能力（即处理新数据的能力）的技术，它通过在有限的训练数据中反复进行"划分-验证" 来实现。

最常用的方法：k折交叉验证

我们以最常用的 5折交叉验证 为例，它的流程如下图所示：
原始训练数据集 随机平均分成5份
Fold 1, Fold 2, ..., Fold 5 第1轮: 以 Fold 1 为验证集
其余4份为训练集 第2轮: 以 Fold 2 为验证集
其余4份为训练集 第3轮: 以 Fold 3 为验证集
其余4份为训练集 第4轮: 以 Fold 4 为验证集
其余4份为训练集 第5轮: 以 Fold 5 为验证集
其余4份为训练集 计算5次验证结果的
平均得分作为最终性能评估

  1. 划分： 将原始训练数据集随机打乱，并平均分成5个互不重叠的子集，称为"折"。
  2. 训练与验证： 进行5次模型训练和评估：
    • 第1次： 使用第2、3、4、5折作为训练集，用第1折作为验证集来评估模型。
    • 第2次： 使用第1、3、4、5折作为训练集，用第2折作为验证集。
    • ... 以此类推，直到每一折都恰好有一次作为验证集。
  3. 汇总结果： 将这5次评估的结果（例如准确率）取平均值，作为模型性能的最终稳健估计。

为什么需要交叉验证？

  • 避免单一划分的偶然性： 如果只做一次训练集/测试集的划分，可能会因为划分方式的不同而导致评估结果差异很大。
  • 充分利用数据： 在数据量有限时，如果单纯留出一部分作为测试集，会减少用于训练的数据量。交叉验证让每个数据点都既参与了训练，也参与了一次验证，物尽其用。

第二部分：为什么随机森林"无需额外分割数据"？------ 袋外误差的妙处

现在我们来理解随机森林和它的"内置交叉验证"------袋外误差。

1. 随机森林的构建核心：Bootstrap抽样

随机森林由许多棵决策树组成。在构建每一棵树 时，它并不是使用全部的原始训练数据，而是采用 Bootstrap抽样（有放回抽样）。

  • 假设原始训练集有N个样本。
  • 对于每一棵树，从这N个样本中随机抽取N次（每次抽一个，然后放回）。
  • 这样，每个树的训练集大小仍然是N，但其中大约有63.2% 的样本会被抽到，而剩下的大约36.8% 的样本永远不会被抽到。

这些没有被抽到的样本 ，就称为这棵树的 "袋外数据"。

2. 袋外误差 就是 "内置的交叉验证"

对于随机森林中的每一棵树：

  • 训练集： 通过Bootstrap抽样得到的样本。
  • 验证集： 该树对应的袋外数据。

评估过程如下：

  1. 当随机森林中所有树都训练完成后，对于每一个样本 （比如样本A），找到所有那些没有用样本A进行训练的树（即样本A是这些树的"袋外数据"）。
  2. 将这些树集合起来，形成一个"小森林"，让这个"小森林"对样本A进行预测。
  3. 将这个小森林的预测结果与样本A的真实标签进行比较。
  4. 对所有样本重复此过程，最终计算出的错误率（对于分类问题是误分率，对于回归问题是均方误差等）就是袋外误差。

为什么说它"无需额外分割数据"？

  • 在传统的机器学习流程中，你需要主动将数据分割为训练集和测试集。
  • 在随机森林中，拜Bootstrap抽样所赐，这个"分割"过程在算法内部自动、随机地完成了。对于每一棵树，系统已经天然地划分好了"训练集"（袋内数据）和"验证集"（袋外数据）。
  • 最终，通过聚合所有树的袋外验证结果，我们得到了一个对模型泛化误差的可靠估计，这个估计的效力类似于k折交叉验证。

总结与类比

特性 传统方法 + 交叉验证 随机森林 + 袋外误差
数据使用 需要用户显式地将数据划分为训练/验证集。 使用全部数据，内部通过Bootstrap自动产生验证集。
验证过程 需要训练k个模型，过程相对繁琐。 与训练过程同步完成，训练结束即可得到验证结果。
计算成本 较高，需要训练模型多次（k次）。 较低，虽然单棵树训练多，但验证是"免费"附送的。
结果可靠性 被广泛认为是可靠的模型评估方法。 经验表明，OOB Error是对模型泛化误差的一个无偏估计，非常可靠。

简单来说，袋外误差是随机森林赠送给我们的一个"免费且高效"的交叉验证工具。 它让我们在不需要额外预留测试集、也不需要手动进行复杂交叉验证的情况下，就能得到一个对模型性能的稳健评估。这正是随机森林算法如此强大和用户友好的原因之一。

2. 代码解释

2.1 代码具体细节解释（函数、参数）

相关推荐
源码之家2 小时前
机器学习：基于python租房推荐系统 预测算法 协同过滤推荐算法 房源信息 可视化 机器学习-线性回归预测模型 Flask框架（源码+文档）✅
大数据·python·算法·机器学习·数据分析·线性回归·推荐算法
小狗照亮每一天7 小时前
【菜狗看背景】自动驾驶发展背景——20251117
人工智能·机器学习·自动驾驶
大白IT7 小时前
智能驾驶：从感知到规控的自动驾驶系统全解析
人工智能·机器学习·自动驾驶
数据与后端架构提升之路7 小时前
英伟达的 Alpamayo-R1：利用因果链推理赋能自动驾驶模型和数据工程剖析
人工智能·机器学习·自动驾驶
维维180-3121-14557 小时前
R语言物种分布建模：算法比较、生态位量化与论文图表制作
r语言·生态学·环境·农业·林业·生物地理
致Great7 小时前
RAG在医疗领域的批判性评估、推荐算法等最新研究进展
算法·机器学习·推荐算法
java1234_小锋8 小时前
[免费]基于python的Flask+Vue医疗疾病数据分析大屏可视化系统（机器学习随机森林算法+requests）【论文+源码+SQL脚本】
python·机器学习·数据分析·flask·疾病数据分析
权泽谦10 小时前
Java 在机器学习中的应用：基于 DL4J 与 Weka 的完整实战案例
java·机器学习·数据挖掘
江塘10 小时前
机器学习-决策树多种生成方法讲解及实战代码讲解(C++/Python实现)
c++·python·决策树·机器学习
热门推荐
01今天 Cloudflare 全球事故，连 GPT 和你的网站都一起“掉线”了02GitHub 镜像站点03UV安装并设置国内源04安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）05BongoCat - 跨平台键盘猫动画工具06Linux下V2Ray安装配置指南07Valdi：Snapchat 开源的新一代跨平台 UI 框架08Labelme从安装到标注：零基础完整指南092025 最新教程：注册并切换到美区 Apple ID10Visual Studio Code设置个性化背景教程