A.每日一题——2536. 子矩阵元素加 1

题目链接：2536. 子矩阵元素加 1（中等）

算法原理：

解法：前缀和+二维差分数组

击败74.85%

时间复杂度O(N²)

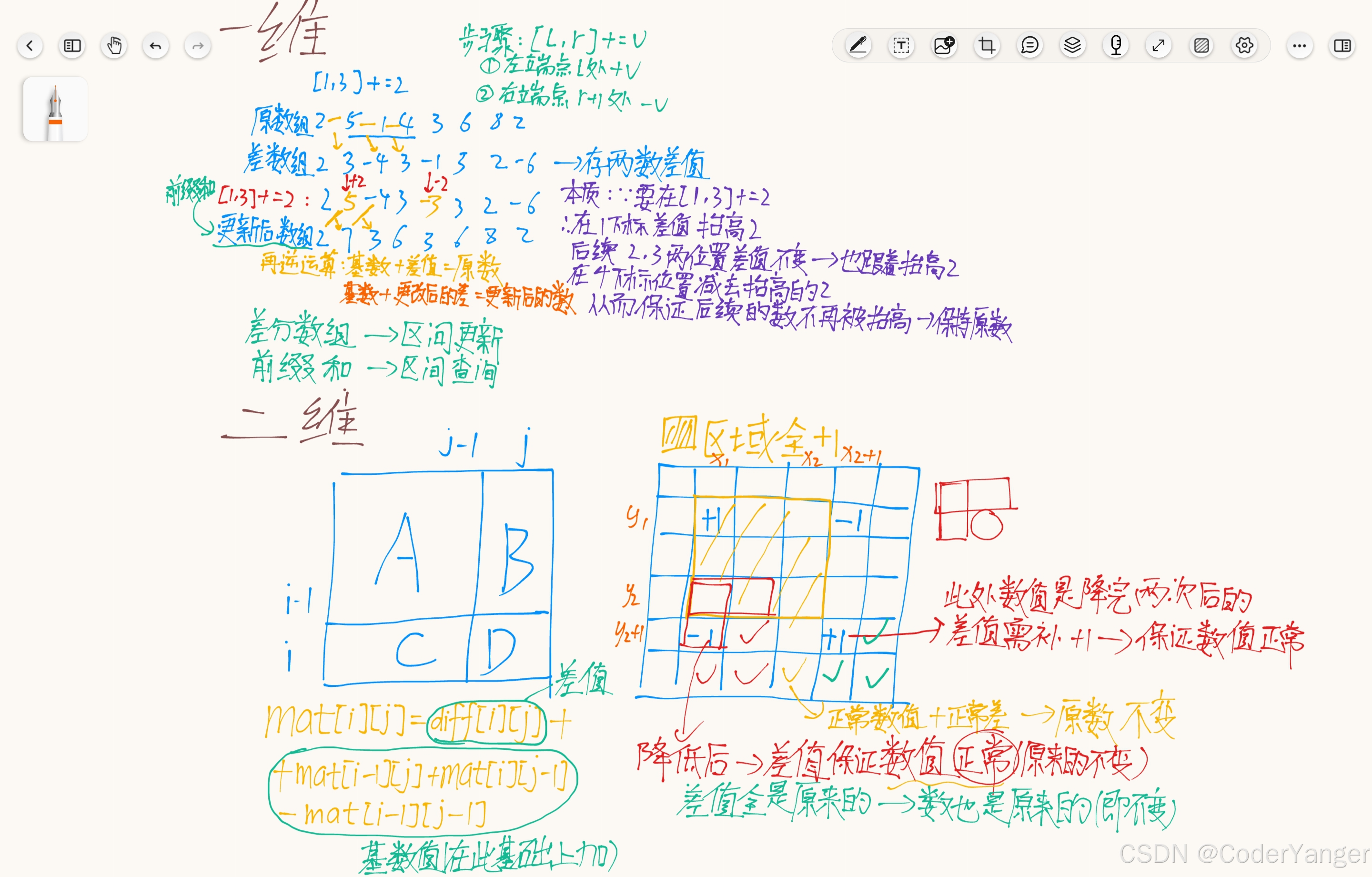
一维和二维的差分数组笔记如下👇

差分算法演示动画（博主就是在这里学习到的🌹）

Java代码：

/**
 * Created with IntelliJ IDEA.
 * Description:
 * User: 王洋
 * Date: 2025-11-14
 * Time: 10:58
 */
class Solution {
    //2536. 子矩阵元素加 1
    //自己第一次的正确但超时的代码
    public int[][] rangeAddQueries(int n, int[][] queries) {
        int[][] ret=new int[n][n];
        for(int k=0;k<queries.length;k++){
            int x1=queries[k][0],y1=queries[k][1],
                    x2=queries[k][2],y2=queries[k][3];
            for(int i=0;i<n;i++)
                for(int j=0;j<n;j++)
                    if(x1<=i&&i<=x2&&y1<=j&&j<=y2)
                        ret[i][j]++;
        }
        return ret;
    }

    //研究了三四个小时，新学到了前缀和算法中的差分数组算法
    //第一个for循环可以换成for-each循环，一样的
    public int[][] rangeAddQueries2(int n, int[][] queries) {
        int[][] diff=new int[n+1][n+1];
        for(int k=0;k<queries.length;k++){
            int x1=queries[k][0],y1=queries[k][1],
                    x2=queries[k][2],y2=queries[k][3];
            diff[x1][y1]+=1;
            diff[x2+1][y2+1]+=1;
            diff[x1][y2+1]-=1;
            diff[x2+1][y1]-=1;
        }
        int[][] mat=new int[n][n];
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                //计算三个区域的前缀和
                int k1=(i==0?0:mat[i-1][j]);//计算（A+B区域）
                int k2=(j==0?0:mat[i][j-1]);//计算（A+C区域）
                int k3=(i==0||j==0)?0:mat[i-1][j-1];//计算A区域
                mat[i][j]=diff[i][j]+k1+k2-k3;
            }
        }
        return mat;
    }
}