图论专题(十三)：“边界”的救赎——逆向思维解救「被围绕的区域」

哈喽各位，我是前端小L。

欢迎来到我们的图论专题第十三篇！在网格图论中，有一类经典问题总是围绕着"包围 "与"逃离"展开。

在这道题中，我们面临着一场"围棋"般的局势。棋盘上布满了 X 和 O。规则是：任何被 X 完全包围 （无法到达边界）的 O，都会被"吃掉"（变成 X）。而那些连接着边界 的 O，则能"逃过一劫"。

我们的任务，就是根据这个规则，更新整个棋盘的状态。

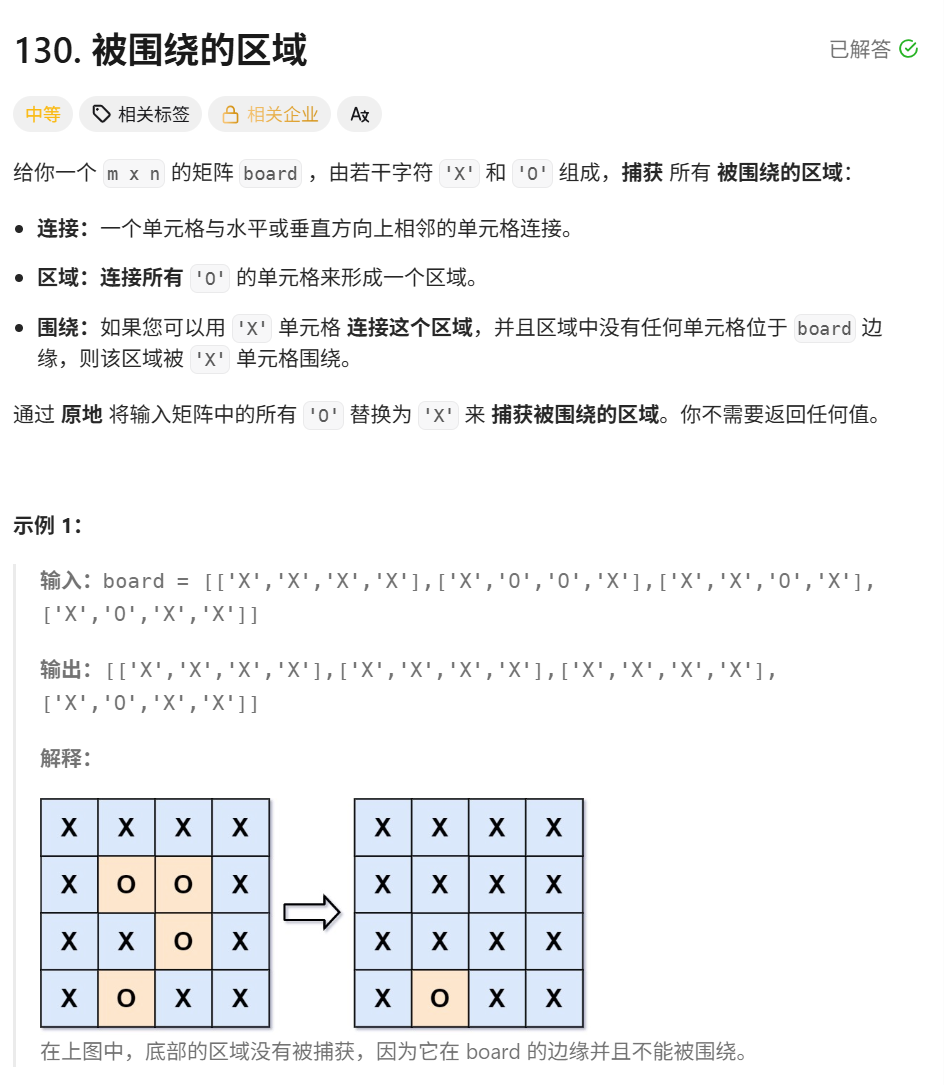
力扣 130. 被围绕的区域

https://leetcode.cn/problems/surrounded-regions/

题目分析：

输入：一个 m x n 的矩阵 board，包含 'X' 和 'O'。
规则：
- 被围绕的区间 ：不会连接到边界的 'O' 区域。
- 操作：将被围绕的 'O' 替换为 'X'。
核心推论：
- 任何在边界上 的 'O'，一定不会被包围。
- 任何与边界上的 'O' 相连 的内部 'O'，也一定不会被包围（它们有一条通往边界的"生路"）。
- 只有那些孤立在内部，切断了与边界所有联系的 'O'，才会被"吃掉"。

思路："逆向思维"------先救人，再清理

如果我们直接遍历内部的 'O'，然后试图通过 DFS/BFS 判断它是否连接边界，这会非常麻烦（每次都要搜索一遍）。

"Aha!"时刻： 与其费力去寻找"必死"的 O，不如先找出所有"幸存 "的 O！所有的"幸存者"，都有一个共同点：它们的"根"都在边界上。

算法流程 (三步走)：

"救援行动" (边界感染)：
- 遍历棋盘的四条边界。
- 只要发现一个 'O'，它就是"幸存者"的入口。
- 启动一次 DFS/BFS ，顺藤摸瓜，找到所有与它相连的 'O'。
- 将这些"幸存"的 'O' 暂时标记 为一个特殊字符，比如 '#' (代表 "Safe")。
"清理战场" (全局扫描)：
- 遍历整个棋盘。
- if (board[r][c] == 'O')：说明这个 'O' 既不在边界，也没连通到边界（否则它早就在第一步被标记成 '#' 了）。它就是"必死"的，把它改成 'X'。
- if (board[r][c] == '#')：说明这是刚才被我们"救援"下来的幸存者。把它还原回 'O'。
任务完成！

代码实现 (DFS)

这个逻辑和 LC 1254 如出一辙，只是最后多了一步"还原/修改"的操作。

C++

复制代码

#include <vector>

using namespace std;

class Solution {
private:
    // "救援队"：DFS 函数
    // 任务：从 (r, c) 出发，标记所有相连的 'O' 为 '#' (Safe)
    void dfs_save(vector<vector<char>>& board, int r, int c) {
        int m = board.size();
        int n = board[0].size();

        // 1. Base Case
        // 越界，或者不是 'O' (可能是 'X' 或已经被标记为 '#')
        if (r < 0 || r >= m || c < 0 || c >= n || board[r][c] != 'O') {
            return;
        }

        // 2. "标记" (救援)
        board[r][c] = '#';

        // 3. 递归探索邻居
        dfs_save(board, r + 1, c);
        dfs_save(board, r - 1, c);
        dfs_save(board, r, c + 1);
        dfs_save(board, r, c - 1);
    }

public:
    void solve(vector<vector<char>>& board) {
        if (board.empty() || board[0].empty()) {
            return;
        }

        int m = board.size();
        int n = board[0].size();

        // --- 第一步："救援行动" (从边界出发) ---
        
        // 遍历左、右边界
        for (int r = 0; r < m; ++r) {
            if (board[r][0] == 'O') dfs_save(board, r, 0);
            if (board[r][n - 1] == 'O') dfs_save(board, r, n - 1);
        }
        
        // 遍历上、下边界
        for (int c = 0; c < n; ++c) {
            if (board[0][c] == 'O') dfs_save(board, 0, c);
            if (board[m - 1][c] == 'O') dfs_save(board, m - 1, c);
        }

        // --- 第二步："清理战场" (替换字符) ---
        for (int r = 0; r < m; ++r) {
            for (int c = 0; c < n; ++c) {
                if (board[r][c] == 'O') {
                    // 没被救援的 O，变成 X
                    board[r][c] = 'X';
                } else if (board[r][c] == '#') {
                    // 被救援的 #，还原为 O
                    board[r][c] = 'O';
                }
            }
        }
    }
};

深度复杂度分析

时间复杂度 O(m * n)：
- "救援"阶段：最坏情况下（全都是O），DFS 会访问每个格子一次。
- "清理"阶段：我们遍历了整个网格一次。
- 总时间 O(m*n)。
空间复杂度 O(m * n)：
- 我们是"原地修改"，不需要 visited 数组。
- 空间开销来自 DFS 的递归栈 。在最坏情况下（"蛇形"全O），递归深度可达 m * n。

总结

今天这道题，再次强化了图论中处理"边界问题"的黄金法则：

从边界出发！

这种"从边缘向中心"渗透的逆向思维，是解决所有"被包围"、"封闭区域"、"边缘流出"等问题的核心。

LC 1254 (统计封闭岛屿)：从边界出发，把连通的陆地"淹没"，剩下的就是封闭的。
LC 130 (被围绕的区域) ：从边界出发，把连通的 O "标记"，剩下的 O 就是被包围的。

掌握了这个模板，你对网格图论的理解就又深了一层。在下一篇中，我们将遇到这个模型的"双重叠加"版本------当我们要同时考虑"太平洋"和"大西洋"两个边界时，该怎么办？

下期见！