方格取数

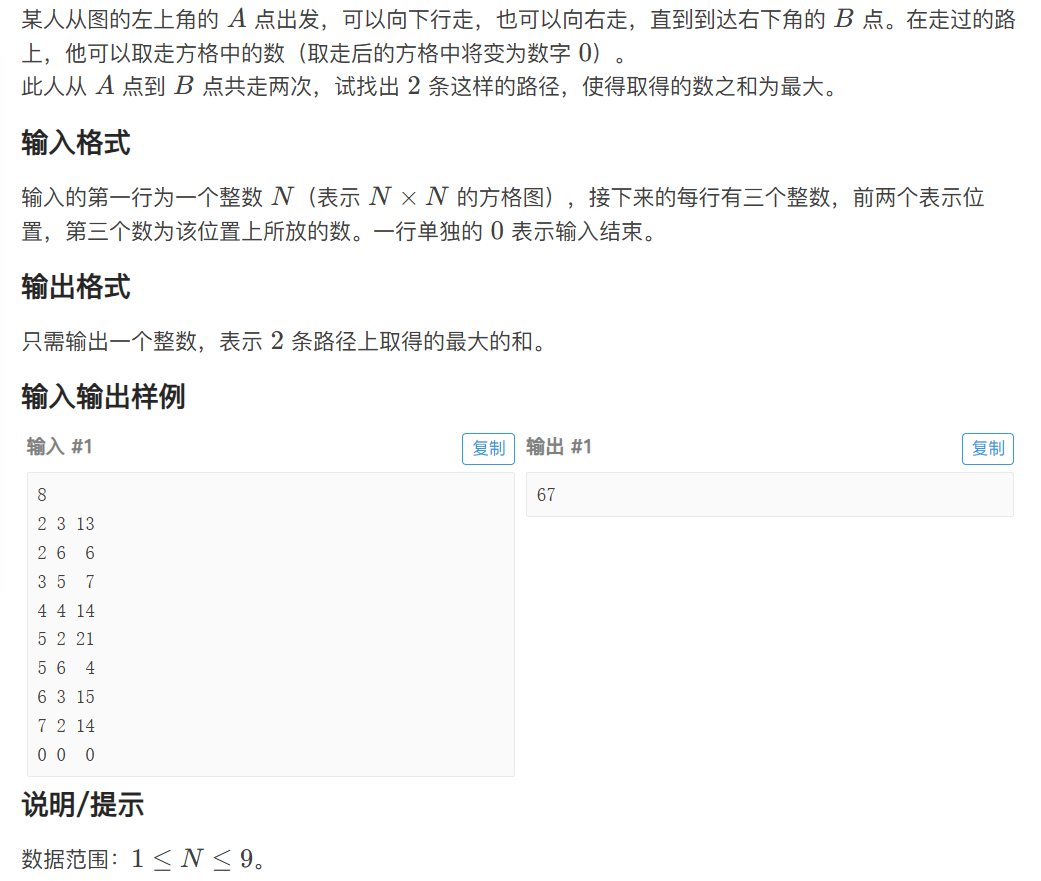
这道题我首先想到用二维数组,二维的思路偏向贪心算法,即定义dp[ i ][ j ]为走到点[ i , j ]时的最佳选项,此时保证第一遍走的时候为最佳答案,第二遍走时为去掉第一遍走过的点时的最佳答案,保证两遍都是分别的最佳答案但非整体的最佳答案......也就是说由于第一遍是只走当前最优的,容易导致第二遍走时取不到更好的值(有只能向下或向右走的限制)。然后会发现我们无法全部走完,也正符合贪心策略,"只注重眼前的利益",因此此题使用二维dp绝非正解。代码如下。
二维dp
cpp
#include<bits/stdc++.h>
using namespace std;
const int N=11;
int dp1[N][N],dp2[N][N],n,o;
struct point
{
int x;
int y;
int num;
}poi[N*N];
void find(int k,int l)//判断第一遍走过哪些点
{
if(k==0&&l==0)
{
return;
}
else
{
if(dp1[k][l]-dp2[k][l]==dp1[k-1][l])
{
dp2[k][l]=0;
find(k-1,l);
}
else if(dp1[k][l]-dp2[k][l]==dp1[k][l-1])
{
dp2[k][l]=0;
find(k,l-1);
}
}
}
int main()
{
scanf("%d",&n);
for(;;)
{
o++;
scanf("%d%d%d",&poi[o].x,&poi[o].y,&poi[o].num);
if(poi[o].x==poi[o].y&&poi[o].y==poi[o].num&&poi[o].num==0)
{
break;
}
else
{
dp1[poi[o].x][poi[o].y]=poi[o].num;
dp2[poi[o].x][poi[o].y]=poi[o].num;
}
}
for(int i=1;i<=n;i++)//第一遍的最优解
{
for(int j=1;j<=n;j++)
{
dp1[i][j]+=max(dp1[i-1][j],dp1[i][j-1]);
}
}
find(n,n);
for(int i=1;i<=n;i++)//第二遍的最优解
{
for(int j=1;j<=n;j++)
{
dp2[i][j]+=max(dp2[i-1][j],dp2[i][j-1]);
}
}
printf("%d",dp1[n][n]+dp2[n][n]);//输出答案
return 0;
}因此我搜题解学习了动态规划的dp,这道题应该应用4维dp。
-
状态:定义一个四维数组 f,f[i][j][k][l]表示第一次走到第 i 行,第 j 列,第二次到达第 k 行,第 l 列能获得的最大值。
-
状态转移方程:我们要考虑以下四种情况:
-
第一次从左边过来,第二次从左边过来
-
第一次从左边过来,第二次从上边过来
-
第一次从上边过来,第二次从左边过来
-
第一次从上边过来,第二次从上边过来
那么我们就要取这四种情况的最大值了,即:f[i][j][k][l] = max(max(f[i-1][j][k-1][l],f[i-1][j][k][l-1]),max(f[i][j-1][k-1][l],f[i][j-1][k][l-1])) + a[i][j] + a[k][l]。
但要注意的是,如果 (i,j)=(k,l),那么就只能加其中一个(不能重复),所以此时要在原来的基础上减去一个a[i][j]。
3.初始化:刚开始也就是到点 (1,1) 能获得的最大值,即f[1][1][1][1]=0。
4.答案:由于我们要求第一次和第二次走到右下角的最大值,所以我们的答案为 f[n][n][n][n]。
四维dp
cpp
#include<bits/stdc++.h>
using namespace std;
int n,x,y,z,a[12][12] = {0},f[12][12][12][12];//表示第一次走到第i行,第j列,第二次到达第k行,第l列能获得的最大值。
int main()
{
cin >> n;
cin >> x >> y >> z ;
while(x!=0||y!=0||z!=0)
{
a[x][y] = z;
cin >> x >> y >> z ;
}
for(int i=1; i<=n; i++)
{
for(int j=1; j<=n; j++)
{
for(int k=1; k<=n; k++)
{
for(int l=1; l<=n; l++)
{
f[i][j][k][l] = max(max(f[i-1][j][k-1][l],f[i-1][j][k][l-1]),max(f[i][j-1][k-1][l],f[i][j-1][k][l-1])) + a[i][j] + a[k][l];
if(i == k && j == l) f[i][j][k][l] -= a[i][j];//如果位置相同,则减去其中一个
}
}
}
}
cout << f[n][n][n][n] << endl;
return 0;
}矩阵取数游戏
/
求n行最大得分和,每一行取数又不会影响到其他行,那么只要确保每一行得分最大,管好自家孩子就行了。(这个在动规中叫最优子结构)
每次取数是在边缘取,那么每次取数完剩下来的元素一定是在一个完整的一个区间中,又是求最优解,区间DP应运而生。
首先明确每行怎么取是没关联的,所以可以看成 n 行每行跑一次区间 dp。对于每行,设 fl,r 表示取区间 l 到 r 的最大值,这明显从大区间向小区间转移,但这里说一下从小区间向大区间转移。
对于一个区间,它乘的 2i 的这个 i 是第 i 次取数,就应等于区间长度,一个长度为 len 的区间从 len−1 转移得到,所以每次转移乘 2 就可以解决答案乘 2i 的问题。这里要好好体会。
记 ai 表示这一行的第 i 个数,对于区间 l 到 r,可以先取 al,可以先取 ar,转移是 fl,r=max(fl+1,r+al,fl,r−1+ar)×2。
答案就是 n 次 f1,m 之和。
cpp
#include <bits/stdc++.h>
using namespace std;
int n, m, a[90][90];
__int128 f[90][90], ans;
void out (__int128 x) {
if(x>9) out(x/10);
putchar(x%10+'0');
}
int main () {
cin >> n >> m;
for (int i=1; i<=n; ++i)
for (int j=1; j<=m; ++j)
cin >> a[i][j];
for (int i=1; i<=n; ans+=f[1][m], memset(f, 0, sizeof f), ++i)
for (int len=1; len<=m; ++len)
for (int l=1, r=l+len-1; r<=m; ++l, ++r)
f[l][r]=max(f[l+1][r]+a[i][l], f[l][r-1]+a[i][r])*2;
out(ans);
return 0;
}