
在算法世界里,排序算法是基础中的基础,而归并排序凭借其稳定的时间复杂度和清晰的逻辑结构,成为很多开发者学习递归思想的首选案例。今天我们就以 C 语言为工具,从零拆解归并排序的递归实现,带你理解 "分治思想" 如何落地为可执行的代码。
一、归并排序:不止于 "排序" 的分治思想
归并排序的核心逻辑可以用 "分而治之" 四个字概括:
- 分(Divide):将待排序数组从中间拆分为两个子数组,重复此过程,直到每个子数组只包含 1 个元素(单个元素默认有序);
- 治(Conquer):将两个有序的子数组合并为一个有序数组,从最小的子数组开始,逐步合并为完整的有序数组。
这种思想的优势在于时间复杂度的稳定性 ------ 无论原始数组是否有序,归并排序的时间复杂度始终是O(nlogn),这比冒泡排序、插入排序等 O (n²) 级别的算法在大数据量下快得多。而递归,则是实现 "分" 操作最直观的方式。
二、C 语言实现:从代码结构看递归逻辑
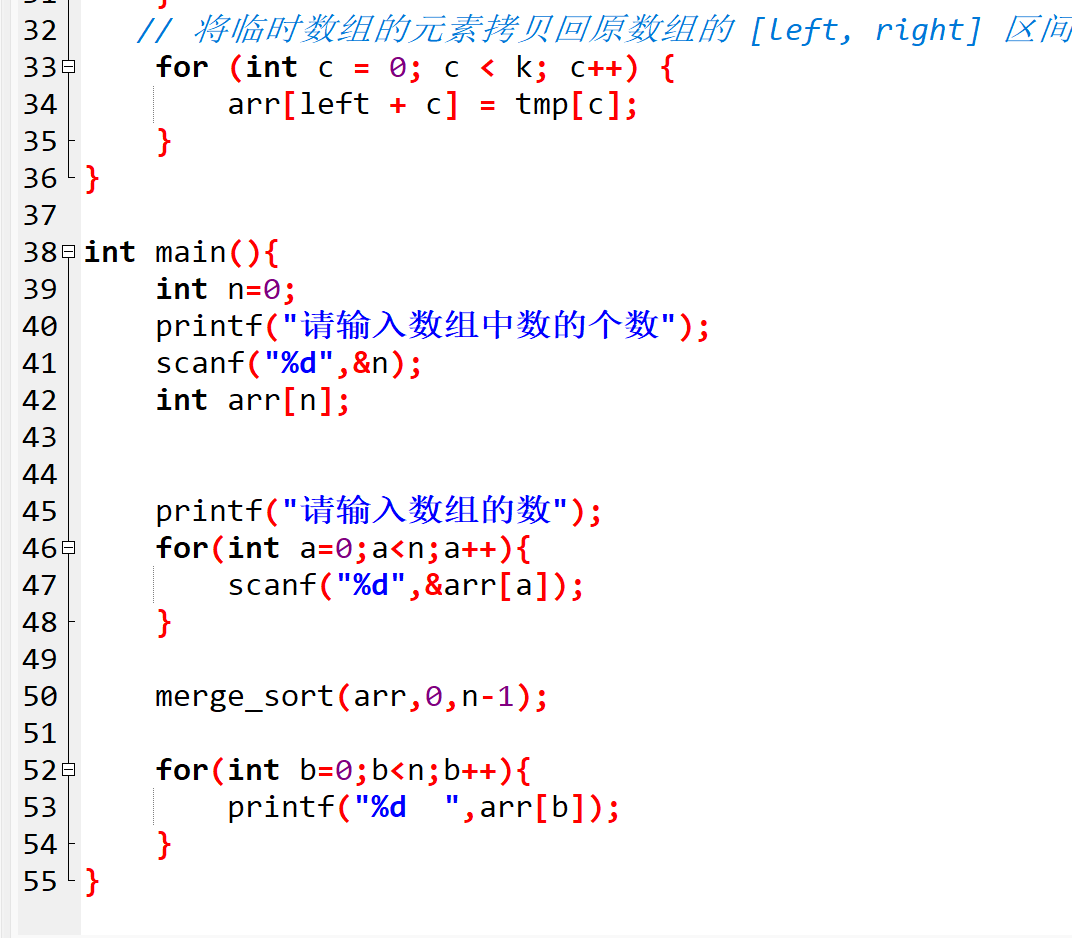
我们先来看完整的 C 语言代码(基于示例优化补充),再逐段拆解关键部分:
#include<stdio.h>
#define A 10000 // 定义临时数组最大长度,避免栈溢出
// 归并排序递归函数:负责拆分与合并
void merge_sort(int arr[], int left, int right) {
// 递归终止条件:当子数组只有1个元素时(left >= right),无需拆分
if (left >= right)
return;
// 1. 分:计算中间索引,避免直接(left+right)/2导致的溢出
int mid = left + (right - left) / 2;
// 递归拆分左子数组 [left, mid]
merge_sort(arr, left, mid);
// 递归拆分右子数组 [mid+1, right]
merge_sort(arr, mid + 1, right);
// 2. 治:合并两个有序子数组
int tmp[A]; // 临时数组,存储合并后的有序元素
int k = 0; // 临时数组的索引指针
int i = left; // 左子数组的起始索引
int j = mid + 1; // 右子数组的起始索引
// 比较两个子数组的元素,按从小到大存入临时数组
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
tmp[k++] = arr[i++]; // 左子数组元素更小,存入临时数组并后移指针
} else {
tmp[k++] = arr[j++]; // 右子数组元素更小,存入临时数组并后移指针
}
}
// 将左子数组中剩余的元素存入临时数组
while (i <= mid) {
tmp[k++] = arr[i++];
}
// 将右子数组中剩余的元素存入临时数组
while (j <= right) {
tmp[k++] = arr[j++];
}
// 3. 把临时数组的有序元素拷贝回原数组的 [left, right] 区间
for (int c = 0; c < k; c++) {
arr[left + c] = tmp[c];
}
}
int main() {
int n = 0;
// 输入数组长度
printf("请输入数组中数的个数:");
scanf("%d", &n);
// 定义变长数组(C99支持),存储待排序元素
int arr[n];
// 输入数组元素
printf("请输入数组的数(用空格分隔):");
for (int a = 0; a < n; a++) {
scanf("%d", &arr[a]);
}
// 调用归并排序:排序区间为整个数组 [0, n-1]
merge_sort(arr, 0, n - 1);
// 输出排序后的结果
printf("排序后的数组:");
for (int b = 0; b < n; b++) {
printf("%d ", arr[b]);
}
return 0;
}
三、关键部分拆解:递归如何 "分",合并如何 "治"
1. 递归函数的核心:终止条件与拆分逻辑
merge_sort函数是整个算法的灵魂,它的参数arr是待排序数组,left和right分别代表当前排序区间的左右边界。
- 递归终止条件:if (left >= right)------ 当区间内只有 1 个元素(left == right)或无元素(left > right)时,无需继续拆分,直接返回。这是避免递归无限循环的关键。
- 拆分逻辑:int mid = left + (right - left) / 2------ 计算中间索引mid,将当前区间拆分为[left, mid]和[mid+1, right]。这里不用(left + right)/2是为了防止left和right过大时出现整数溢出(比如left=1e9,right=1e9,直接相加会超出 int 范围)。
- 递归调用:merge_sort(arr, left, mid)和merge_sort(arr, mid+1, right)------ 分别对左、右子数组进行递归拆分,直到触发终止条件。
2. 合并操作:将两个有序数组合为一个
拆分完成后,就进入 "治" 的环节 ------ 把两个有序的子数组合并为一个有序数组。这一步需要借助临时数组tmp,避免直接在原数组上操作导致数据丢失。
合并过程分为三步:
- 双指针比较合并:用i指向左子数组的起始位置,j指向右子数组的起始位置,比较arr[i]和arr[j]的大小,将更小的元素存入tmp,并移动对应的指针(i++或j++)和临时数组指针(k++)。
- 处理剩余元素:当其中一个子数组的元素全部存入tmp后,将另一个子数组中剩余的元素直接追加到tmp末尾(因为子数组本身是有序的,剩余元素必然比tmp中已有的元素大)。
- 拷贝回原数组:将tmp中存储的有序元素,按原区间[left, right]拷贝回原数组arr,完成当前区间的排序。
四、代码运行与优化思考
1. 实际运行效果
假设我们输入:
请输入数组中数的个数:5
请输入数组的数(用空格分隔):3 1 4 2 5
代码会经过递归拆分(拆分为[3]、[1]、[4]、[2]、[5]),再逐步合并:
- 合并[3]和[1] → [1,3];
- 合并[4]和[2] → [2,4];
- 合并[1,3]和[2,4] → [1,2,3,4];
- 最后合并[1,2,3,4]和[5] → [1,2,3,4,5]。
最终输出:排序后的数组:1 2 3 4 5,符合预期。
2. 可优化的方向
示例代码虽能正常运行,但仍有提升空间:
- 临时数组的定义:当前tmp是在函数内定义的局部数组,每次递归调用都会创建一个新数组,可能导致栈内存占用过高。可以将tmp改为全局数组,或在main函数中定义后作为参数传入merge_sort,减少内存开销。
- 变长数组的兼容性:int arr[n]是 C99 标准支持的变长数组(VLA),但部分编译器(如旧版 MSVC)不支持。若需兼容更多环境,可改用动态内存分配(malloc)创建数组。
- 数据规模限制:#define A 10000限定了临时数组的最大长度,若排序数据量超过 10000,会导致数组越界。可根据实际需求调整A的值,或动态计算临时数组的长度。
五、总结:递归与分治的启示
通过 C 语言实现归并排序,我们不仅学会了一种高效的排序算法,更理解了递归思想的本质 ------将复杂问题拆解为多个相同的子问题,解决子问题后再整合结果。递归的关键在于明确 "终止条件" 和 "子问题边界",而归并排序的 "分" 与 "治",正是这一思想的完美体现。
如果你是算法初学者,建议多调试代码:在merge_sort函数中加入printf语句,观察left、mid、right的变化,就能直观看到递归的拆分过程。动手实践后,你会发现 "递归" 不再是抽象的概念,而是可以掌控的代码逻辑。