内容包括:memcpy memmove memset memcmp函数 什么是大小端?
memcpy

这个函数比strcpy区别就是我们strcmp是拷贝字符串的,但是如果我想拷贝数组或者是其他的类型就不可以,所以我们引用了memcpy这个函数
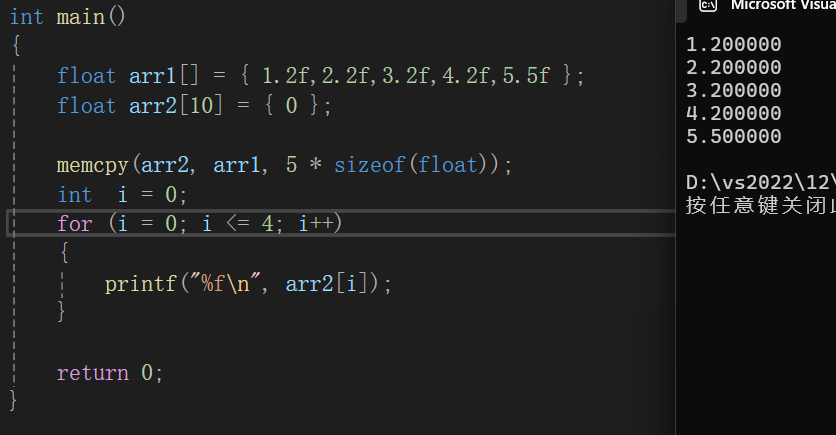
memcpy模拟实现
cs
void* my_memcpy(void* dest, void* str,size_t num)
//这里不确定是什么类型,以后可能会传入不同类型,所以我们传入void类型
{
assert(dest && str); //断言
void* p = dest; //记录dest起始地址
while (num--)
{
*(char*)dest = *(char*)str; //每次传入一次地址
dest = (char*)dest + 1;
str = (char*)str + 1;
}
return p; //返回目标的起始地址
}
int main()
{
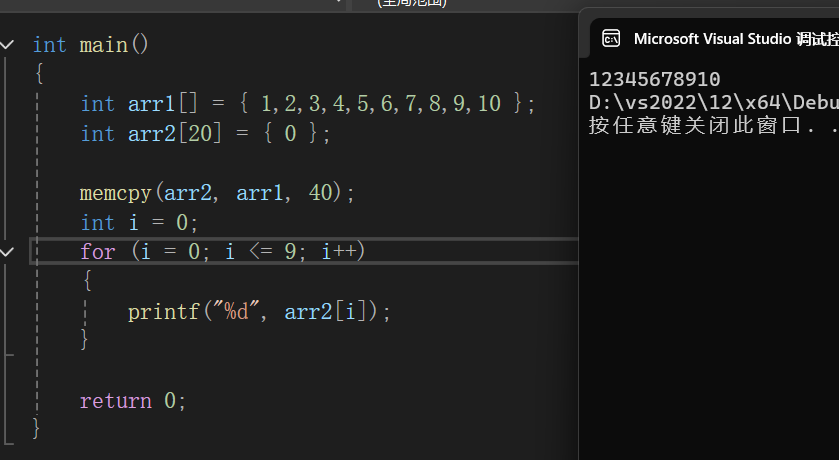
int arr1[] = { 1,2,3,4,5,6,7,8,9,10 };
int arr2[20] = { 0 };
my_memcpy(arr2, arr1, 40); //10个整形有40个字节,返回后arr2已经复制完成
int i = 0;
for (i = 0; i <= 9; i++) //所以我们打印就好了
{
printf("%d", arr2[i]);
}
return 0;
}但是这个拷贝是不可以重叠的,只不过在vs可以实现
memmove
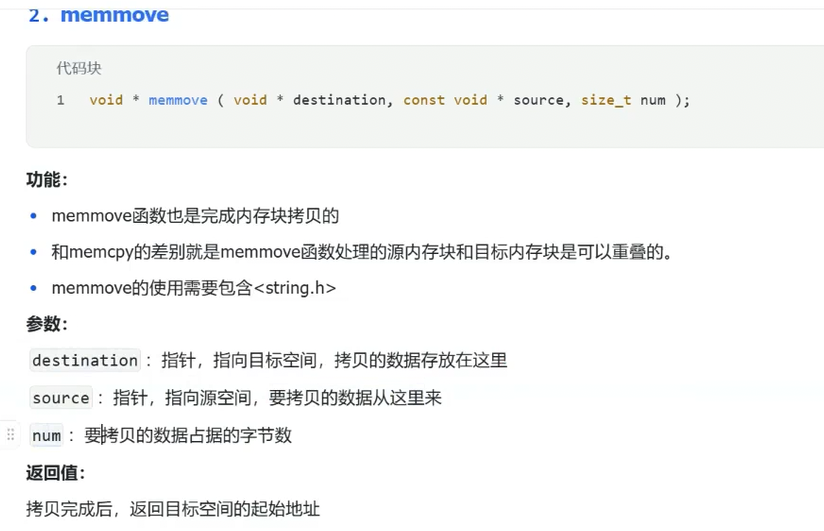
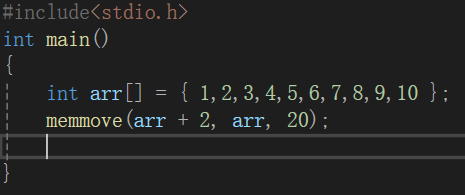
这个就是重叠了
memmove的模拟实现
第一种:如果源空间地址比目标空间小,就可以采用str中后面的5到7,4到6,3到5,2到4,1到3
就是所谓的后向前拷贝
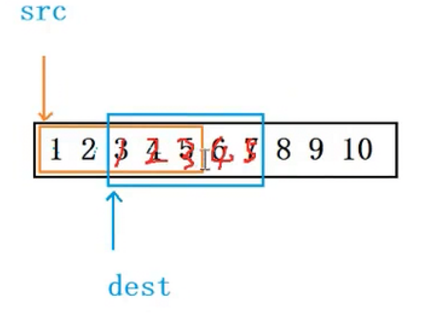
第二种:如果源空间地址比目标空间大,就可以采用str的前面向后面拷贝
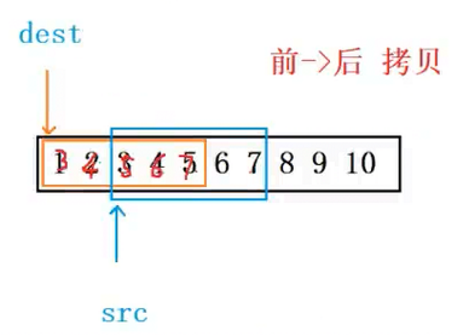
cs
#include <assert.h>
#include<stdio.h>
#include<string.h>
void* my_memmove(void* dest, const void* src, size_t num)
{
assert(dest && src); //断言
void* ret = dest; //无类型指针初始化ret记录起始地址
if (dest < src) //目标空间小,采用前到后
{
// 前->后
while (num--)
{
*(char*)dest = *(char*)src;
dest = (char*)dest + 1;
src = (char*)src + 1;
}
}
else
{
// 后->前
while (num--)
{
*((char*)dest + num) = *((char*)src + num);
//这个时候这两个地址都是str和dest的最后地址,然后开始后到前
}
}
return ret; //返回目标的起始地址
}
int main()
{
// 内存重叠
int arr[] = { 1,2,3,4,5,6,7,8,9,10 };
my_memmove(arr, arr + 2, 20);
int i = 0;
for (i = 0; i <= 9; i++)
{
printf("%d", arr[i]);
}
return 0;
}memset函数
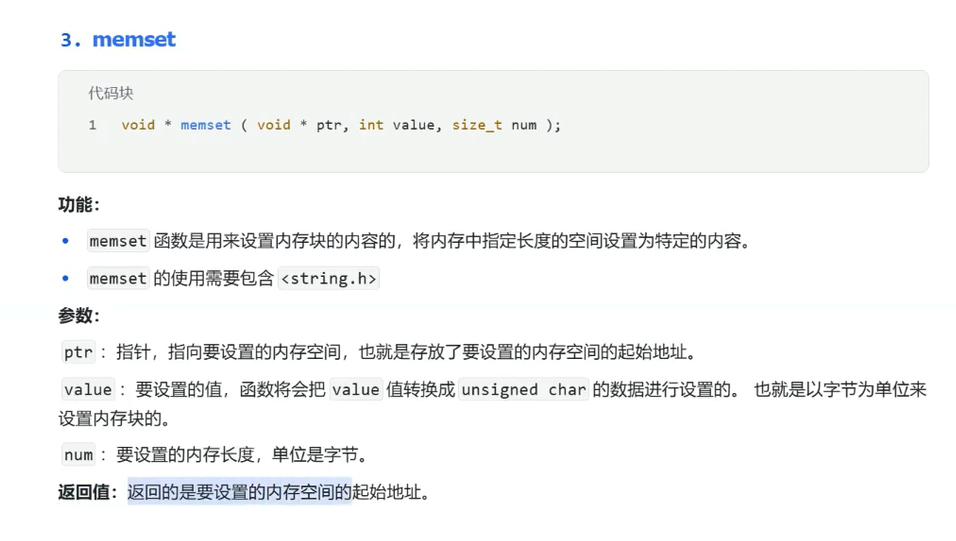
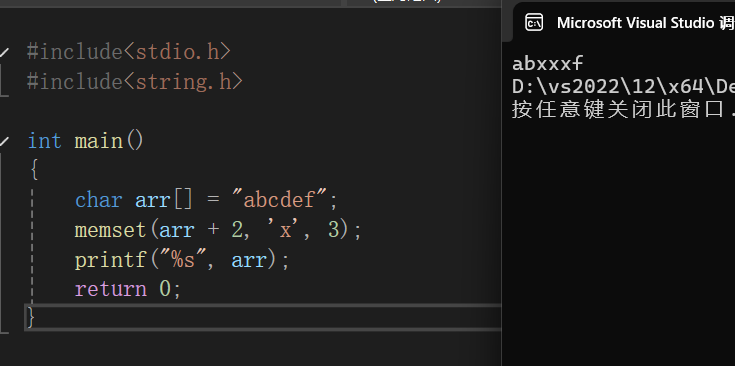
那我们可以把1替换成arr[10]中的0吗?
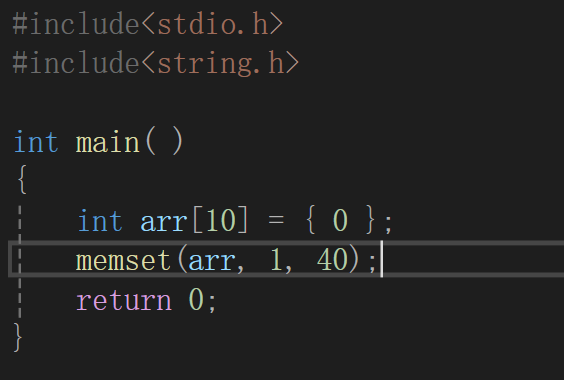
是不行的:因为在计算机中存放一般是十六进制数字,1也就是0x 00 00 00 01
但是如果我们替换的是1,就会导致是0x 01 01 01 01
memcmp函数
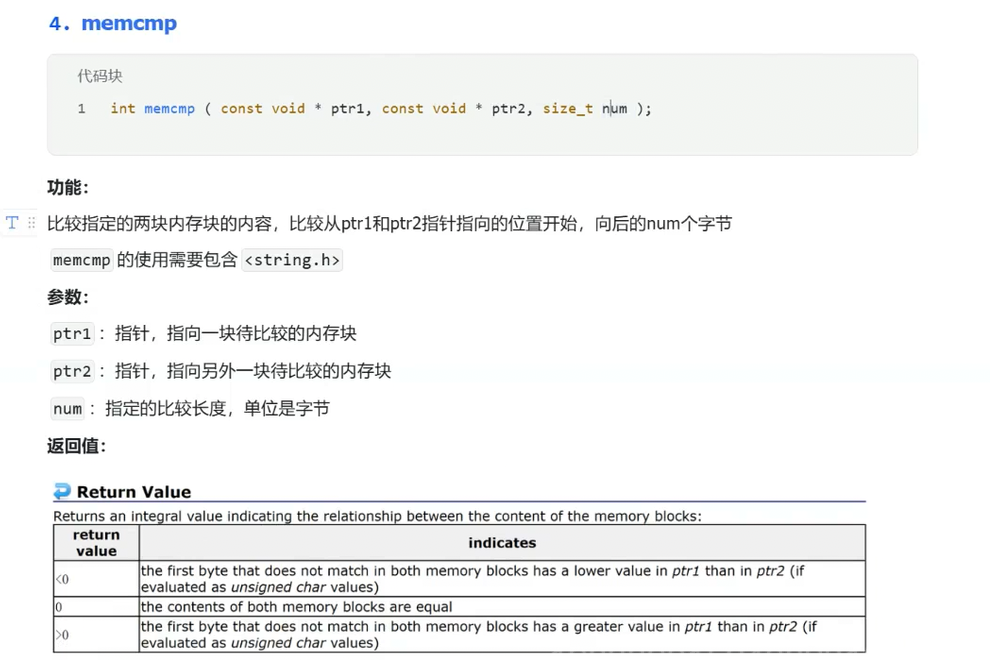
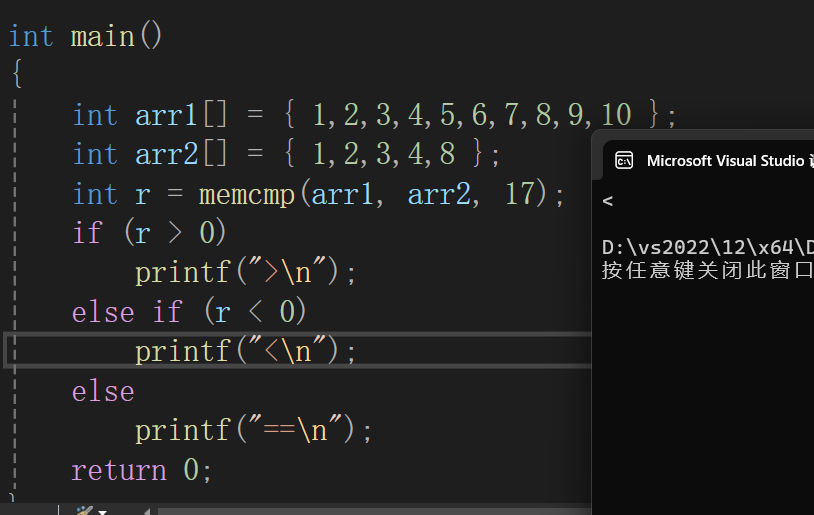
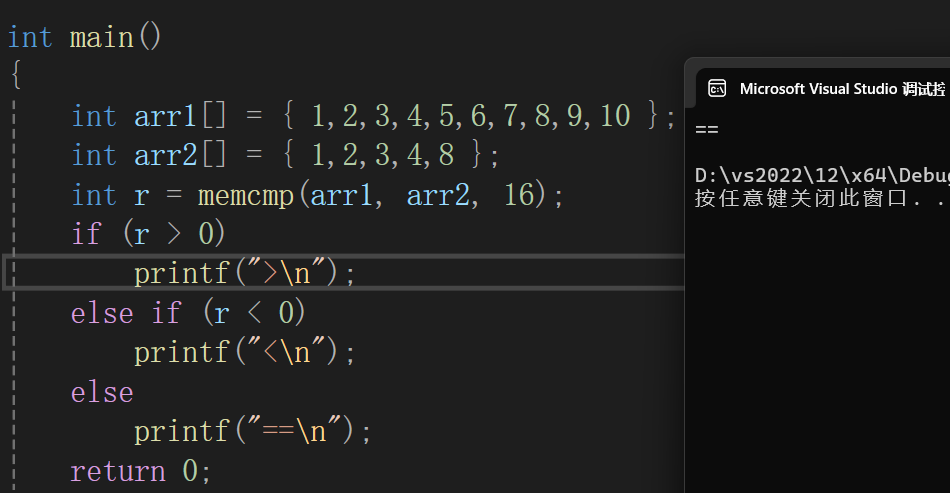
什么是大小端?
其实超过一个字节的数据在内存中存储的时候,就有存储顺序的问题,按照不同的存储顺序,我们分为大端字节序存储和小端字节序存储,下面是具体的概念:
大端(存储)模式:是指数据的低位字节内容保存在内存的高地址处,而数据的高位字节内容,保存在内存的低地址处。
小端(存储)模式:是指数据的低位字节内容保存在内存的低地址处,而数据的高位字节内容,保存在内存的高地址处
举个例子:
int b =0x 11 22 33 44
大端:11 22 33 44 小端: 44 33 22 11
为什么会有大小端模式之分呢?这是因为在计算机系统中,我们是以字节为单位的,每个地址单元都对应着一个字节,一个字节为 8 bit 位,但是在 C 语言中除了 8 bit 的 char 之外,还有 16 bit 的 short 型,32 bit 的 long 型(要看具体的编译器),另外,对于位数大于 8 位的处理器,例如 16 位或者 32 位的处理器,由于寄存器宽度大于一个字节,那么必然存在着一个如何将多个字节安排的问题。因此就导致了大端存储模式和小端存储模式
例如:一个 16bit 的 short 型 x,在内存中的地址为 0x0010,x 的值为 0x1122,那么 0x11 为高字节,0x22 为低字节。对于大端模式,就将 0x11 放在低地址中,即 0x0010 中,0x22 放在高地址中,即 0x0011 中。小端模式,刚好相反。我们常用的 X86 结构是小端模式,而 KEIL C51 则为大端模式。很多的 ARM,DSP 都为小端模式。有些 ARM 处理器还可以由硬件来选择是大端模式还是小端模式

cs
#include <stdio.h>
int main()
{
int a = 1;
if (*(char*)&a == 1) //这个就是一个字节,00就是一个字节 00 00 00 01就是4个字节,一个整形
{
printf("小端\n");
}
else
{
printf("大端\n");
}
return 0;
}现在我们来看看不同类型数据的存储范围
cs
#include <stdio.h>
int main()
{
char a = -1;
signed char b = -1;
unsigned char c = -1;
printf("a = %d, b = %d, c = %d", a, b, c);
return 0;
}
这是为什么呢?
首先我们来讲一下下面的知识点


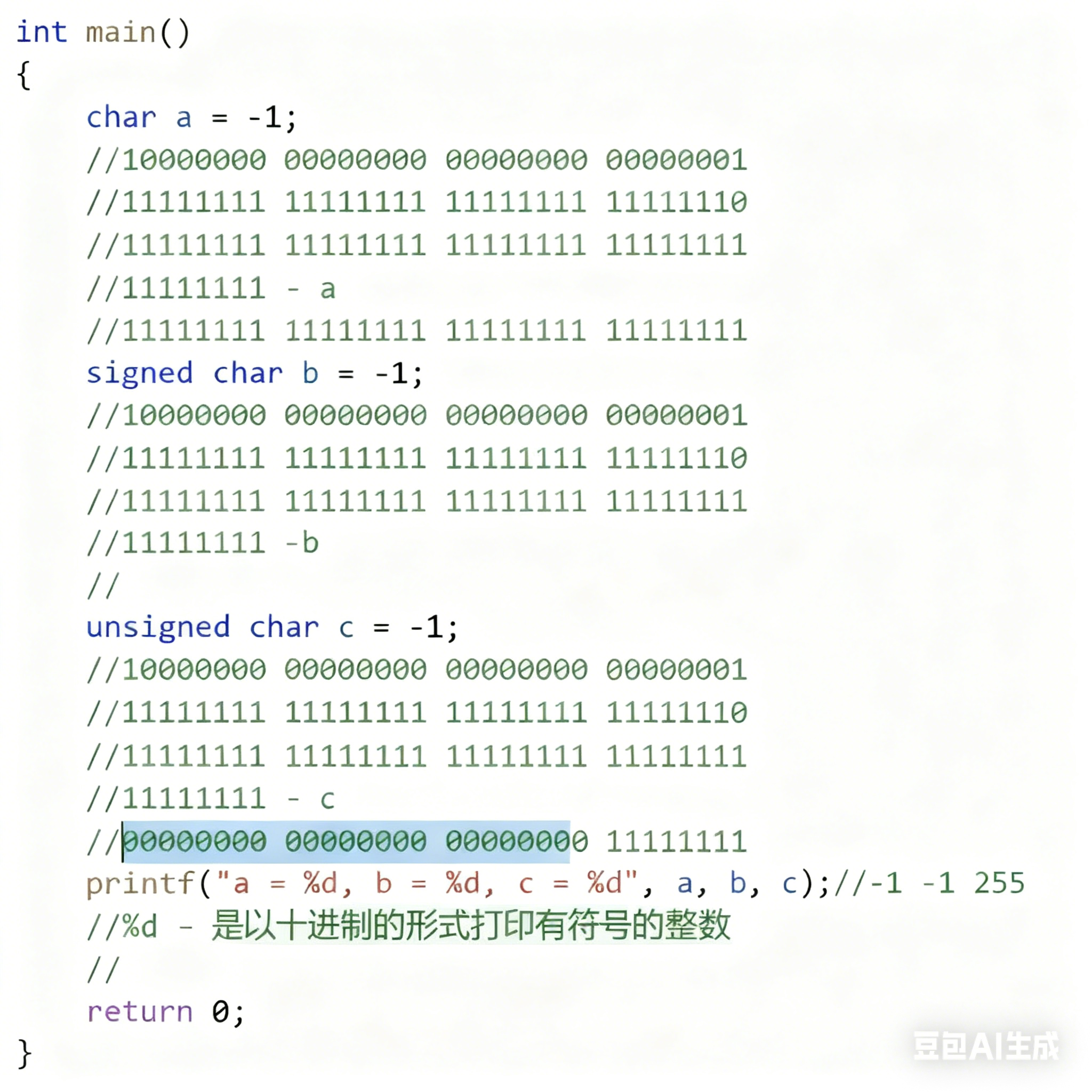
整形提升:有符号整形是按照符号位提升,无符号整形是按照0提升
我们还有一种是%u进行打印也就是无符号的整数进行打印

我们看这个,在有符号的整形的时候,我们需要把下面111111111111111111111111转化为原码打印出来,但是如果是无符号整形的时候,我们就可以直接打印,因为没有符号这一说法,所以无符号打印出来的结果非常大:
现在我们看几道题目
第一道:
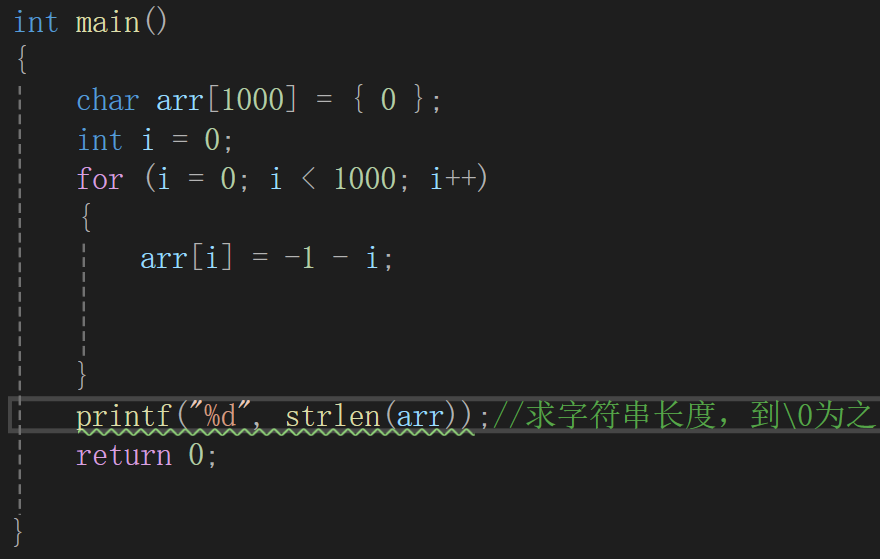
正常输出的arr应该是:-1,-2,-3 ~~~~~~~ ,-128,-129~~~~~~~-1001
但是我们会发现其实char的范围没有这么高:-128到127
所以我们发现下面的排布应该是这样的:-128直接就到了127,没有-129了
这个是因为其实-129和127在计算机中的补码在提取char类型的8位bite是一样的
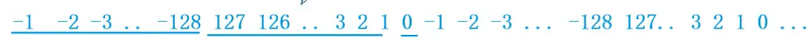
所以从-1到-128,然后127到0就结束了,因为到0了,\0的ascill值就是0,所以加在一起就是128+127=
第二道题:
cs
#include <stdio.h>
unsigned char i = 0;
int main()
{
for (i = 0; i <= 255; i++)
{
printf("%u: hello world\n", i);
}
return 0;
}结果是什么?
其实是死循环的,因为unsigned char 的范围是0~255,而上面的i<255是恒成立的,所以for循环是不会跳出去,也就导致死循环
第三题:
cs
#include <stdio.h>
int main()
{
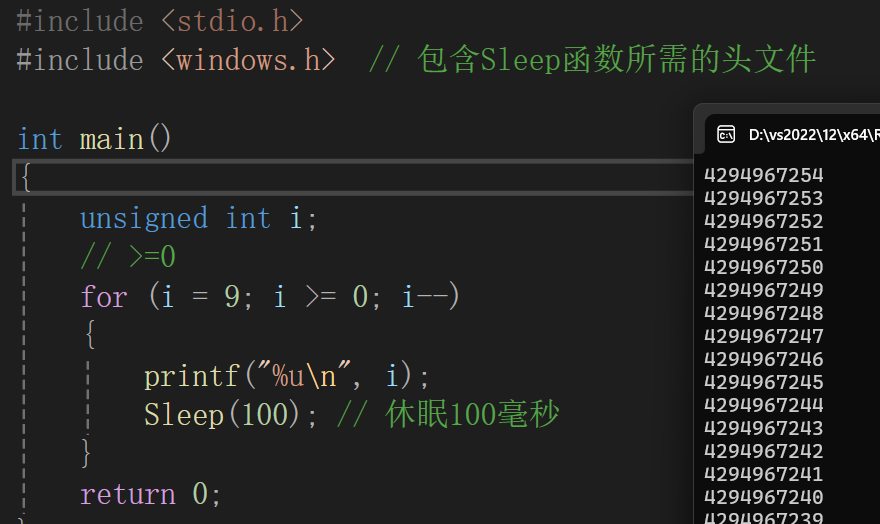
unsigned int i;
for (i = 9; i >= 0; i--)
{
printf("%u\n", i);
}
return 0;
}结果也是死循环,因为unsigned int 绝对大于0,所以i>0恒成立,跳不出循环
我们加入休眠语句让代码刷新慢一点