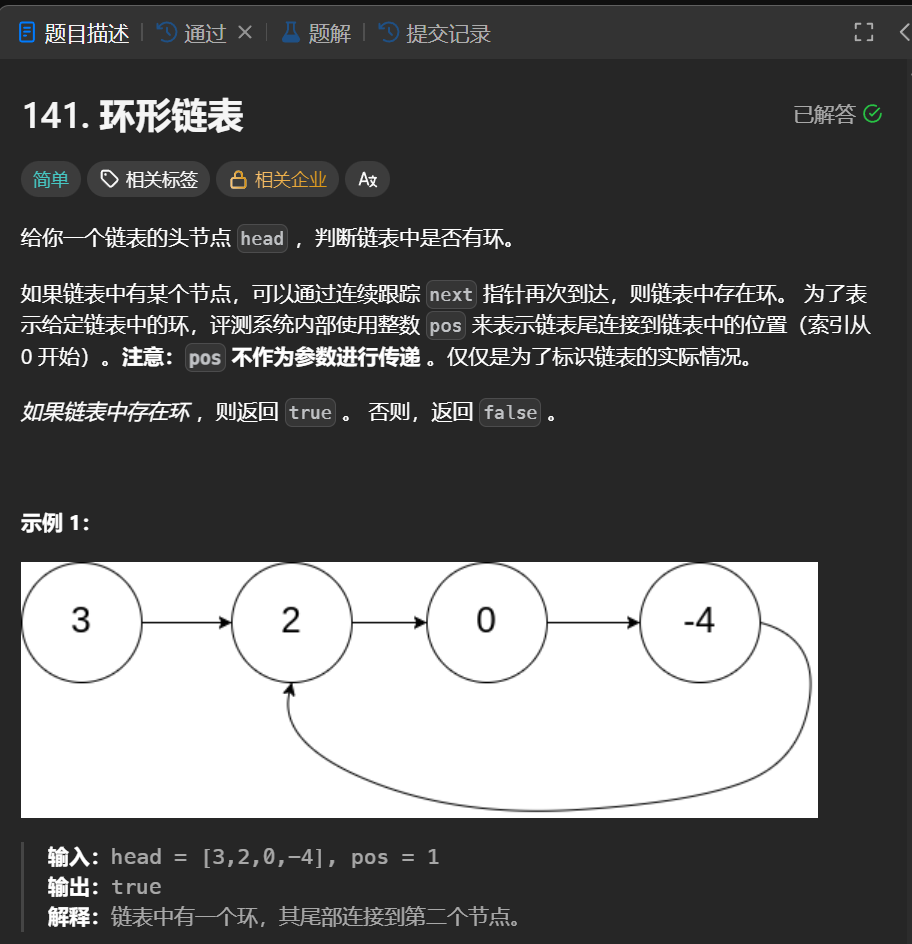
这是一个经典的链表问题,通常被称为"判断链表是否有环"。
解决这个问题的标准且最高效的解法是 快慢指针算法(也称为 Floyd 判圈算法或龟兔赛跑算法)。
解题思路
-
定义两个指针:
-
慢指针 (
slow):一次走一步。 -
快指针 (
fast):一次走两步。
-
-
逻辑分析:
-
如果没有环 :
fast指针走得快,最终会遇到NULL(即到达链表末尾),此时可以直接返回false。 -
如果有环 :
fast指针会率先进入环,并在环内循环。当slow指针也进入环后,这就变成了一个"追及问题"。因为fast比slow每次多走一步,所以在有限的步数内,fast一定会追上slow(即fast == slow)。
-
-
复杂度:
-
时间复杂度:O(n)。如果无环,遍历一次;如果有环,快指针在环内绕圈追上慢指针的时间也是线性的。
-
空间复杂度:O(1)。只使用了两个指针,不需要额外的哈希表来存储已访问的节点。
-
下面是完整的代码实现,包含了解题类和用于构建带环链表进行测试的 main 函数。
代码要点
-
初始化 :
slow和fast都指向head。有些写法会让fast初始指向head->next,这也是可以的,但循环条件和判断逻辑稍微不同。让它们都从head开始是最直观的。 -
循环条件 :
while (fast != NULL && fast->next != NULL)。这个条件非常关键,它保证了fast->next->next不会出现空指针异常。 -
相遇判断 :在移动指针之后立即检查
if (slow == fast)。如果相等,说明快指针追上了慢指针,链表有环。 -
返回结果:如果循环正常退出,说明快指针遇到了空指针,链表没有环。
cpp
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
bool hasCycle(ListNode *head) {
if(head == NULL || head->next == NULL)
return false;
ListNode* fast = head;
ListNode* slow = head;
while(fast != nullptr && fast->next != nullptr)
{
slow = slow->next;
fast = fast->next->next;
if(slow == fast)
return true;
}
return false;
}
};