在数据结构的世界里,单链表就像一条灵活的 "链子",它由一个个 "链节"(节点)串联而成,能够高效地存储和操作数据。相比于数组,单链表在数据插入、删除等操作上具有独特的优势,尤其当数据量动态变化时,单链表的灵活性更是凸显。今天,我们就以 C 语言为工具,将抽象的单链表概念转化为具体的代码实现,再结合 "链子" 的形象比喻,带大家一步步揭开单链表的神秘面纱。
一、单链表是什么?用 "链子" 帮你理解
在开始代码之旅前,我们先搞清楚单链表到底是什么。其实,单链表的结构和生活中的链子非常相似。想象一下,一条普通的链子,它由许多个独立的链节组成,每个链节都有两个部分:一部分是链节本身的 "内容"(比如链节的材质、形状),另一部分是和下一个链节连接的 "接口"。单链表的结构与此如出一辙。
单链表中的每个 "链节" 被称为节点(Node),每个节点也包含两个部分:
- 数据域(data):就像链节的 "内容",用于存储具体的数据,比如整数、字符、结构体等(本文以整数类型为例)。
- 指针域(next):相当于链节的 "接口",它是一个指针,指向链表中的下一个节点,通过这个指针,各个节点才能串联起来,形成一条完整的 "数据链子"。
此外,单链表通常还会有一个头节点(head)。头节点就像是链子的 "开端",它本身一般不存储实际的数据(也可以存储链表长度等辅助信息),主要作用是方便我们对链表进行操作,比如找到链表的起始位置、统一链表的插入和删除逻辑等。
为了更直观地理解,大家可以想象这样一张 "链子图":最左边是头节点(标注 "头节点,data=0(辅助信息)"),头节点的指针域指向第一个存储数据的节点(比如 data=18);第一个节点的指针域又指向第二个节点(data=88);第二个节点的指针域指向第三个节点(data=888);最后一个节点的指针域指向 "NULL"(表示链子的末尾,没有下一个节点了)。通过这张图,我们就能清晰地看到单链表中各个节点的连接关系,抽象的概念瞬间就变得具体了。
二、C 语言实现单链表:从 "链节" 到 "整条链子"
理解了单链表的结构后,我们就用 C 语言来一步步实现它。整个实现过程就像 "打造一条链子",先制作单个的 "链节"(定义节点结构体),然后搭建 "链子的开端"(初始化链表),再实现 "添加链节"(插入节点)、"去掉链节"(删除节点)、"查看链子"(遍历链表)等操作,最后还要记得 "拆解链子"(释放内存),避免内存泄漏。
1. 第一步:定义 "链节"------ 节点结构体
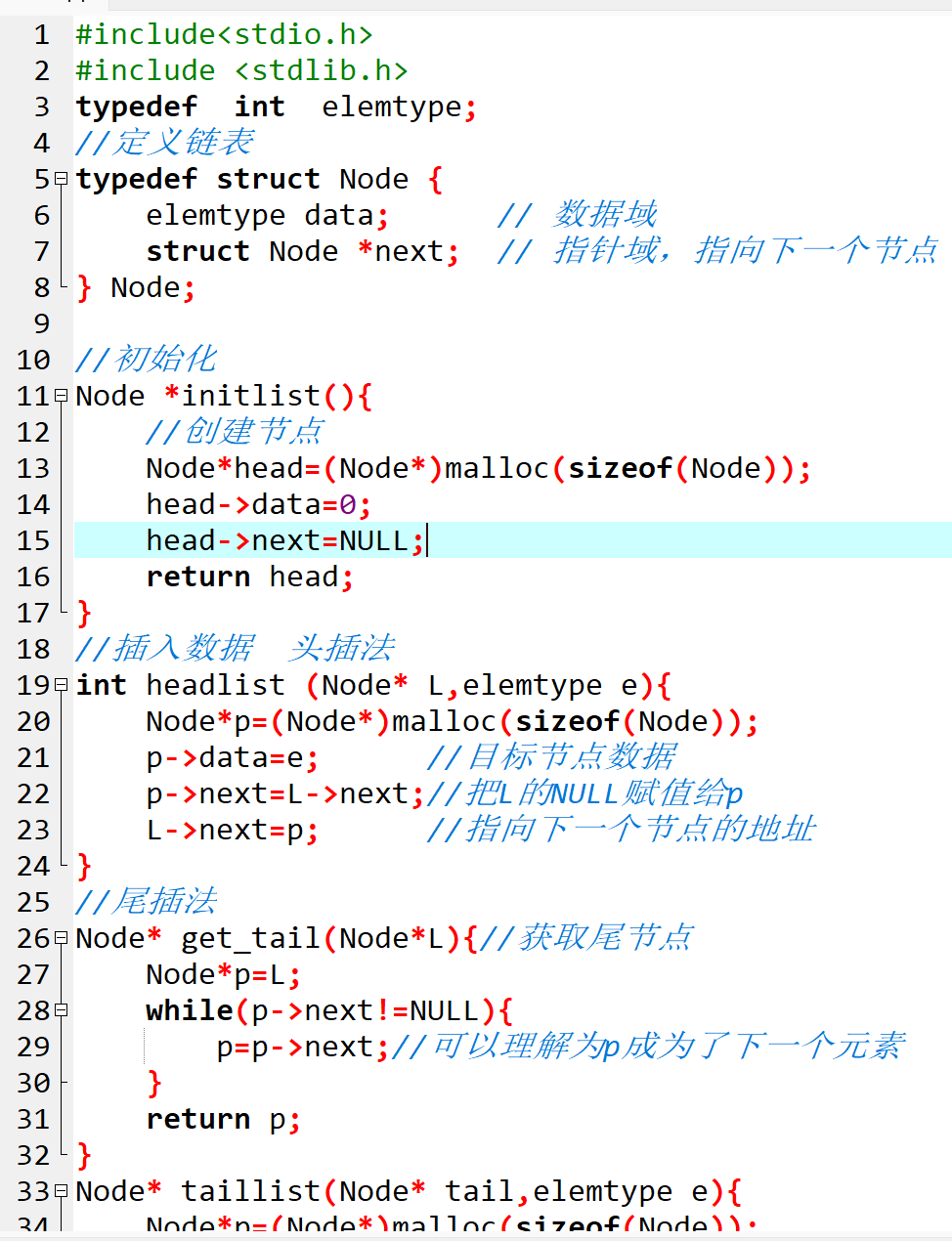
要制作 "链节",首先得明确每个 "链节" 的组成。在 C 语言中,我们用结构体(struct)来定义节点,结构体中包含数据域和指针域。代码如下:
// 定义数据类型,这里以整数为例,后续若要存储其他类型,只需修改此处
typedef int elemtype;
// 定义链表节点结构体(链节)
typedef struct Node {
elemtype data; // 数据域:存储具体数据,相当于链节的"内容"
struct Node *next; // 指针域:指向 next 节点,相当于链节的"连接接口"
} Node;
这里用typedef给结构体起了别名 "Node",后续定义节点变量或指针时会更简洁。elemtype也是一个自定义类型,我们将其定义为int,如果后续需要存储其他类型(如float、char),只需修改typedef int elemtype;这一行即可,体现了代码的可扩展性。
2. 第二步:搭建 "链子开端"------ 初始化链表
打造链子前,我们需要先确定链子的 "开端"(头节点)。初始化链表的作用就是创建一个头节点,并将头节点的指针域设置为NULL(表示刚开始,链子还没有后续的 "链节"),同时可以给头节点的 data 域赋值(比如赋值为 0,用于存储链表长度等辅助信息,也可以不存储实际数据)。代码实现如下:
// 初始化链表:创建头节点,返回头节点指针(链子的开端)
Node *initlist() {
// 为头节点分配内存空间(相当于制作一个"开端链节")
Node *head = (Node *)malloc(sizeof(Node));
// 头节点 data 域赋值为 0(可作为链表长度的初始值,也可作为辅助标记)
head->data = 0;
// 头节点的 next 指针指向 NULL(表示目前链子只有"开端",没有后续链节)
head->next = NULL;
// 返回头节点指针,后续操作链表都从这个"开端"开始
return head;
}
这里用到了malloc函数为头节点分配内存,malloc(sizeof(Node))表示申请一块大小为Node结构体的内存空间,然后将其强制转换为Node *类型(因为malloc返回的是void *类型),最后赋值给头节点指针head。初始化完成后,我们就有了链表的 "开端",接下来就可以往这条 "链子" 上添加 "链节" 了。
3. 第三步:"添加链节"------ 三种插入节点的方式
往链子上添加 "链节"(节点)有三种常见的方式:头插法(在链子的开端后面添加)、尾插法(在链子的末尾添加)、精准插入(在链子的指定位置添加)。每种方式适用的场景不同,我们逐一来看。
(1)头插法:在 "链子开端" 后快速添加链节
头插法的特点是 "每次都在头节点的后面插入新节点",就像在链子的 "开端" 后面直接接上一个新的链节。这种方式的优点是插入速度快,不需要遍历整个链表,只需修改指针的指向即可。代码实现如下:
// 头插法:在头节点后面插入新节点(e 为要插入的数据)
int headlist(Node *L, elemtype e) {
// 为新节点分配内存空间(制作一个新的"链节")
Node *p = (Node *)malloc(sizeof(Node));
// 给新节点的 data 域赋值(设置新链节的"内容")
p->data = e;
// 新节点的 next 指针指向头节点原来的 next 节点(新链节连接到原来的第一个链节)
p->next = L->next;
// 头节点的 next 指针指向新节点(链子的"开端"连接到新链节)
L->next = p;
// 头节点的 data 域加 1(更新链表长度,因为多了一个链节)
L->data++;
// 插入成功,返回 1
return 1;
}
大家可以配合 "链子图" 来理解:原本头节点(L)的 next 指向节点 A,现在插入新节点 p,先让 p 的 next 指向 A(新链节接上原来的第一个链节),再让 L 的 next 指向 p(开端接上新链节),这样新节点就成功插入到了头节点后面。头插法的时间复杂度是 O (1),因为无论链表有多长,插入操作都只需要修改两个指针的指向。
(2)尾插法:在 "链子末尾" 添加链节
尾插法是 "每次都在链表的最后一个节点后面插入新节点",就像在链子的末尾再接上一个新的链节。这种方式插入的节点会按照插入顺序排列,适合需要 "按序存储数据" 的场景。要实现尾插法,首先需要找到链表的 "末尾节点"(尾节点),然后在尾节点后面插入新节点。代码实现如下:
首先,实现 "找尾节点" 的函数:
// 获取链表的尾节点(找到链子的最后一个链节)
Node *get_tail(Node *L) {
// 从链表的头节点开始遍历
Node *p = L;
// 当 p 的 next 不为 NULL 时,说明 p 不是尾节点,继续往后找
while (p->next != NULL) {
p = p->next; // p 移动到下一个节点(沿着链子往后走)
}
// 当 p 的 next 为 NULL 时,p 就是尾节点(链子的最后一个链节)
return p;
}
然后,实现尾插法插入节点的函数:
// 尾插法:在尾节点后面插入新节点(tail 为当前尾节点,e 为要插入的数据)
Node *taillist(Node *tail, elemtype e) {
// 为新节点分配内存空间(制作新链节)
Node *p = (Node *)malloc(sizeof(Node));
// 给新节点的 data 域赋值(设置新链节内容)
p->data = e;
// 尾节点的 next 指针指向新节点(原来的最后一个链节接上新链节)
tail->next = p;
// 新节点的 next 指针指向 NULL(新链节成为新的末尾,后面没有其他链节了)
p->next = NULL;
// 返回新的尾节点(现在新节点是链子的最后一个链节)
return p;
}
尾插法的关键是找到尾节点,找尾节点的过程需要遍历整个链表,所以尾插法的时间复杂度是 O (n)(n 为链表长度)。但尾插法插入的节点是按顺序排列的,比如依次插入 18、88、888,链表中节点的顺序就是 18→88→888,这一点和头插法不同(头插法插入这三个数据,顺序会是 888→88→18)。
(3)精准插入:在 "链子指定位置" 添加链节
有时候,我们需要在链表的指定位置插入节点,比如在第 2 个节点后面插入一个新节点,这就是精准插入。要实现精准插入,首先需要找到 "插入位置的前一个节点"(前驱节点),然后在前驱节点后面插入新节点。代码实现如下:
// 精准插入:在链表的第 pos 个位置插入数据 e(pos 从 1 开始计数)
int insertlist(Node *L, int pos, elemtype e) {
// 检查插入位置是否合法(pos 不能小于 1)
if (pos < 1) {
printf("插入位置不合法!\n");
return 0;
}
// p 指向头节点,用于遍历找到前驱节点
Node *p = L;
// 遍历 pos-1 步,找到第 pos 个节点的前驱节点(第 pos-1 个节点)
for (int i = 0; i < pos - 1; i++) {
// 如果遍历过程中 p 的 next 为 NULL,说明 pos 超出了链表长度,插入位置不合法
if (p->next == NULL) {
printf("插入位置不合法!\n");
return 0;
}
p = p->next; // p 移动到下一个节点
}
// 为新节点分配内存空间(制作新链节)
Node *q = (Node *)malloc(sizeof(Node));
// 给新节点的 data 域赋值
q->data = e;
// 新节点的 next 指针指向前驱节点原来的 next 节点(新链节接上原来的后续链节)
q->next = p->next;
// 前驱节点的 next 指针指向新节点(前驱链节接上新链节)
p->next = q;
// 头节点的 data 域加 1(更新链表长度)
L->data++;
// 插入成功,返回 1
return 1;
}
精准插入的关键是找到前驱节点,这个过程同样需要遍历链表,时间复杂度也是 O (n)。比如我们要在第 2 个位置插入数据 6,假设原链表是 18→88→888,那么前驱节点就是第 1 个节点(data=18),先让新节点 q 的 next 指向第 2 个节点(data=88),再让前驱节点的 next 指向 q,插入后链表就变成了 18→6→88→888,非常直观。
4. 第四步:"去掉链节"------ 删除指定位置的节点
当我们不需要链子上的某个 "链节" 时,就需要将其删除。单链表的删除操作和精准插入类似,首先要找到 "删除节点的前驱节点",然后通过修改指针指向,将删除节点从链表中 "摘下来",最后释放删除节点的内存(避免内存泄漏)。代码实现如下:
// 删除节点:删除链表第 pos 个位置的节点(pos 从 1 开始计数)
int dellist(Node *L, int pos) {
// 检查删除位置是否合法(pos 不能小于 1)
if (pos < 1) {
printf("删除位置不合法!\n");
return 0;
}
// p 指向头节点,用于遍历找到前驱节点
Node *p = L;
// 遍历 pos-1 步,找到第 pos 个节点的前驱节点(第 pos-1 个节点)
for (int i = 0; i < pos - 1; i++) {
// 如果遍历过程中 p 的 next 为 NULL,说明 pos 超出了链表长度,删除位置不合法
if (p->next == NULL) {
printf("删除位置不合法!\n");
return 0;
}
p = p->next; // p 移动到下一个节点
}
// q 指向要删除的节点(前驱节点的 next 节点)
Node *q = p->next;
// 前驱节点的 next 指针指向删除节点的 next 节点(跳过删除节点,把链子重新接起来)
p->next = q->next;
// 释放删除节点的内存(把"摘下来的链节"回收)
free(q);
// 头节点的 data 域减 1(更新链表长度)
L->data--;
// 删除成功,返回 1
return 1;
}
比如我们要删除第 3 个位置的节点,原链表是 18→6→88→888,前驱节点是第 2 个节点(data=6),要删除的节点 q 是第 3 个节点(data=88)。我们让前驱节点的 next 指向 q 的 next 节点(data=888),然后释放 q 的内存,删除后链表就变成了 18→6→888,整个过程就像把链子上的某个链节摘下来,再把前后的链节重新接好。
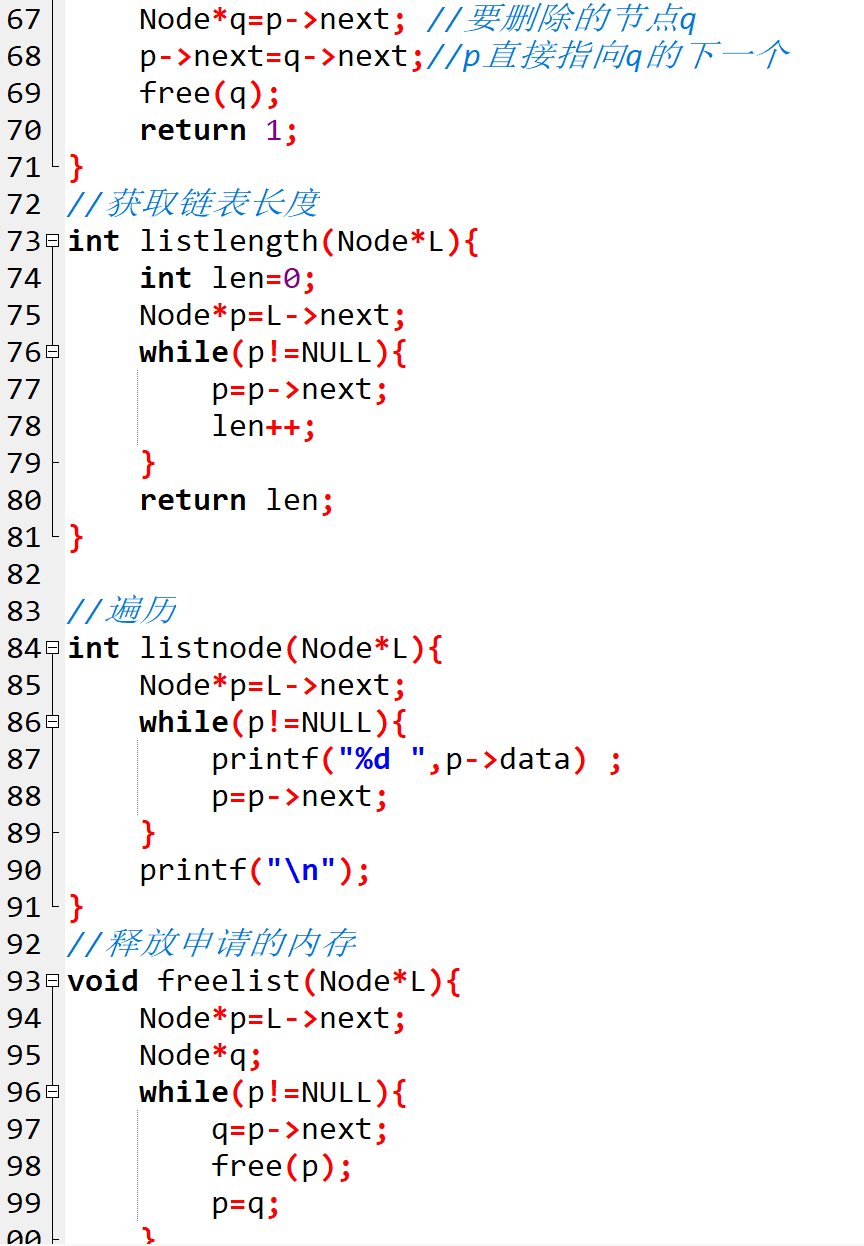
5. 第五步:"查看链子"------ 遍历链表和获取链表长度
制作好链子后,我们需要知道链子上有哪些 "内容"(遍历链表),以及链子有多长(获取链表长度)。这两个操作都需要遍历链表,代码实现如下:
(1)遍历链表:查看链子上的所有 "内容"
// 遍历链表:打印链表中所有节点的数据(查看链子上的内容)
int listnode(Node *L) {
// p 指向头节点的 next 节点(从第一个存储数据的节点开始遍历)
Node *p = L->next;
// 如果 p 为 NULL,说明链表为空(链子上没有链节)
if (p == NULL) {
printf("链表为空!\n");
return 0;
}
// 遍历链表,直到 p 为 NULL(走到链子的末尾)
while (p != NULL) {
// 打印当前节点的数据(查看链节内容)
printf("%d ", p->data);
// p 移动到下一个节点(沿着链子往后走)
p = p->next;
}
// 打印换行符,使输出更整洁
printf("\n");
return 1;
}
遍历链表的过程很简单,就是从第一个存储数据的节点开始,依次往后移动,直到走到链表的末尾(p 为 NULL),并打印每个节点的数据。比如链表是 18→6→888,遍历后会输出 "18 6 888",让我们清晰地看到链表中的数据。
(2)获取链表长度:知道链子有多长
// 获取链表长度:计算链表中存储数据的节点个数(链子的链节数量)
int listlength(Node *L) {
// 初始化长度为 0
int len = 0;
// p 指向头节点的 next 节点(从第一个存储数据的节点开始计数)
Node *p = L->next;
// 遍历链表,每经过一个节点,长度加 1
while (p != NULL) {
p = p->next; // p 移动到下一个节点
len++; // 长度加 1
}
// 返回链表长度(链节数量)
return len;
}
获取链表长度的过程和遍历类似,只是在遍历的同时计数,每经过一个节点,长度就加 1。比如链表是 18→6→888,长度就是 3,这个长度也可以通过头节点的 data 域来获取(因为我们在插入和删除节点时会更新头节点的 data 域),两种方式的结果是一致的,大家可以根据需求选择。
6. 第六步:"拆解链子"------ 释放链表内存
当我们不再需要这条 "链子" 时,一定要记得 "拆解链子",释放掉为每个节点分配的内存,否则会造成内存泄漏(内存被占用但无法使用)。释放内存的过程需要遍历链表,逐个释放每个节点的内存,代码实现如下:
// 释放链表内存:释放所有节点的内存(拆解链子,回收材料)
void freelist(Node *L) {
// p 指向头节点的 next 节点(从第一个存储数据的节点开始释放)
Node *p = L->next;
// q 用于暂存 p 的 next 节点(避免释放 p 后找不到下一个节点)
Node *q;
// 遍历链表,逐个释放节点内存
while (p != NULL) {
q = p->next; // 先暂存 p 的 next 节点(记住下一个链节的位置)
free(p); // 释放当前节点 p 的内存(拆解当前链节)
p = q; // p 移动到下一个节点(准备拆解下一个链节)
}
// 释放完所有节点后,将头节点的 next 指向 NULL(链子拆解完成,开端后面没有链节了)
L->next = NULL;
}
释放内存的过程需要特别注意顺序:先暂存当前节点的 next 节点(q = p->next),再释放当前节点(free (p)),最后让 p 指向 q,这样才能确保遍历不会中断。如果不暂存 next 节点,释放 p 后,p->next 就变成了无效指针,无法找到下一个节点,会导致内存泄漏。
三、完整代码演示:让 "链子" 动起来
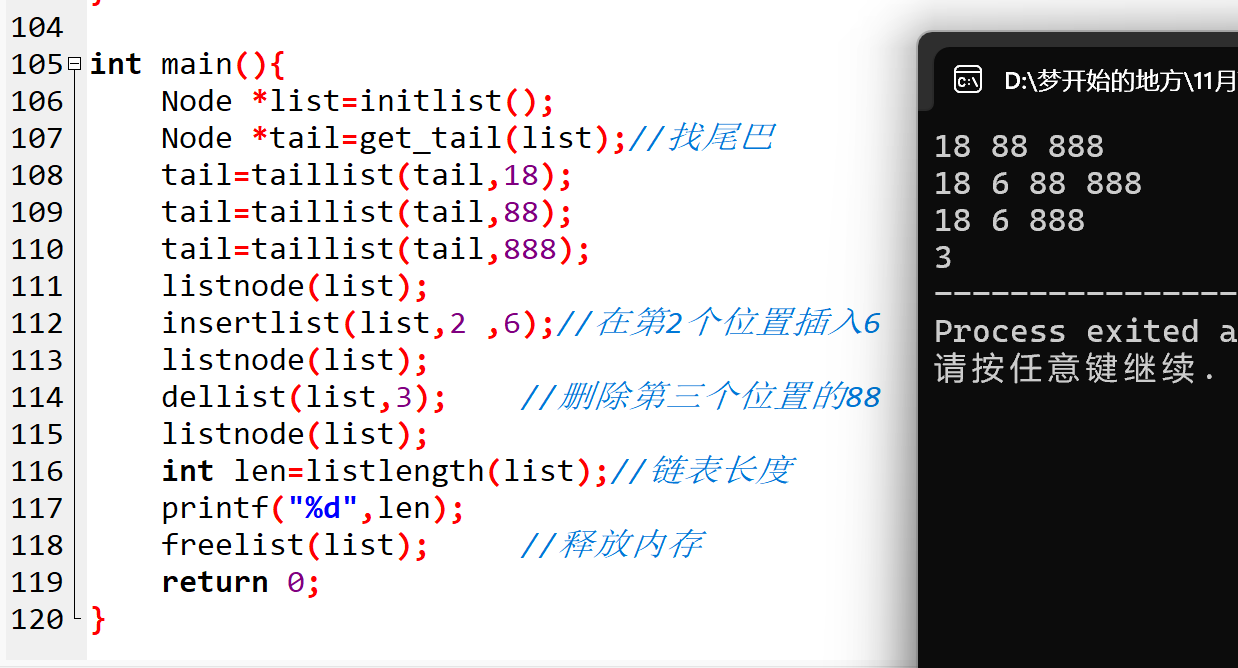
将上面的所有函数组合起来,再加上main函数(作为程序的入口,调用各个函数来操作链表),我们就得到了单链表的完整 C 语言实现代码。下面我们通过一个具体的例子,看看这条 "链子" 是如何 "动起来" 的:
#include<stdio.h>
#include <stdlib.h>
// 定义数据类型
typedef int elemtype;
// 定义链表节点结构体(链节)
typedef struct Node {
elemtype data; // 数据域
struct Node *next; // 指针域
} Node;
// 初始化链表(创建链子开端)
Node *initlist() {
Node *head = (Node *)malloc(sizeof(Node));
head->data = 0;
head->next = NULL;
return head;
}
// 头插法(在开端后添加链节)
int headlist(Node *L, elemtype e) {
Node *p = (Node *)malloc(sizeof(Node));
p->data = e;
p->next = L->next;
L->next = p;
L->data++;
return 1;
}
// 获取尾节点(找到链子末尾)
Node *get_tail(Node *L) {
Node *p = L;
while (p->next != NULL) {
p = p->next;
}
return p;
}
// 尾插法(在末尾添加链节)
Node *taillist(Node *tail, elemtype e) {
Node *p = (Node *)malloc(sizeof(Node));
p->data = e;
tail->next = p;
p->next = NULL;
return p;
}
// 精准插入(在指定位置添加链节)
int insertlist(Node *L, int pos, elemtype e) {
if (pos < 1) {
printf("插入位置不合法!\n");
return 0;
}
Node *p = L;
for (int i = 0; i < pos - 1; i++) {
if (p->next == NULL) {
printf("插入位置不合法!\n");
return 0;
}
p = p->next;
}
Node *q = (Node *)malloc(sizeof(Node));
q->data = e;
q->next = p->next;
p->next = q;
L->data++;
return 1;
}
// 删除节点(去掉指定链节)
int dellist(Node *L, int pos) {
if (pos < 1) {
printf("删除位置不合法!\n");
return 0;
}
Node *p = L;
for (int i = 0; i < pos - 1; i++) {
if (p->next == NULL) {
printf("删除位置不合法!\n");
return 0;
}
p = p->next;
}
Node *q = p->next;
p->next = q->next;
free(q);
L->data--;
return 1;
}
// 获取链表长度(链子长度)
int listlength(Node *L) {
int len = 0;
Node *p = L->next;
while (p != NULL) {
p = p->next;
len++;
}
return len;
}
// 遍历链表(查看链子内容)
int listnode(Node *L) {
Node *p = L->next;
if (p == NULL) {
printf("链表为空!\n");
return 0;
}
while (p != NULL) {
printf("%d ", p->data);
p = p->next;
}
printf("\n");
return 1;
}
// 释放链表内存(拆解链子)
void freelist(Node *L) {
Node *p = L->next;
Node *q;
while (p != NULL) {
q = p->next;
free(p);
p = q;
}
L->next = NULL;
}
// 主函数:程序入口,调用各个函数操作链表
int main() {
// 1. 初始化链表(创建链子开端)
Node *list = initlist();
// 2. 找到尾节点(准备用尾插法添加链节)
Node *tail = get_tail(list);
// 3. 尾插法插入数据 18、88、888(添加三个链节)
tail = taillist(tail, 18);
tail = taillist(tail, 88);
tail = taillist(tail, 888);
// 4. 遍历链表(查看当前链子内容)
printf("尾插法插入后链表内容:");
listnode(list); // 输出:18 88 888
// 5. 精准插入:在第 2 个位置插入数据 6(在第二个链节后添加新链节)
insertlist(list, 2, 6);
// 6. 遍历链表(查看插入后的链子内容)
printf("精准插入后链表内容:");
listnode(list); // 输出:18 6 88 888
// 7. 删除节点:删除第 3 个位置的节点(去掉第三个链节)
dellist(list, 3);
// 8. 遍历链表(查看删除后的链子内容)
printf("删除后链表内容:");
listnode(list); // 输出:18 6 888
// 9. 获取链表长度(查看当前链子的链节数量)
int len = listlength(list);
printf("当前链表长度:%d\n", len); // 输出:3
// 10. 释放链表内存(拆解链子,回收内存)
freelist(list);
return 0;
}
运行这段代码,我们可以看到如下输出结果:
尾插法插入后链表内容:18 88 888
精准插入后链表内容:18 6 88 888
删除后链表内容:18 6 888
当前链表长度:3
这个结果和我们之前的分析完全一致,从初始化链表到插入、删除、遍历、释放内存,整个过程清晰地展示了单链表的操作流程,也让我们感受到了 "链子" 从创建到使用再到拆解的完整生命周期。
四、单链表的优势与不足:什么时候该用 "链子"?
通过前面的学习,我们已经掌握了单链表的实现和操作,接下来我们来分析一下单链表的优势与不足,以便在实际开发中判断什么时候该用单链表("链子"),什么时候该用其他数据结构(如数组)。
1. 单链表的优势("链子" 的优点)
- 动态内存分配:单链表的节点是动态分配内存的,不需要预先确定内存大小,数据量增加时只需添加新节点,数据量减少时只需删除节点并释放内存,内存利用率高,不会造成内存浪费(而数组需要预先分配固定大小的内存,可能会有内存浪费或内存不足的问题)。
- 插入、删除操作高效:在链表的头部或指定位置插入 / 删除节点时,只需修改指针的指向,不需要移动大量数据(数组插入 / 删除数据时,需要移动插入位置后面的所有数据,效率低)。尤其是头插法,时间复杂度是 O (1),非常高效。
- 灵活的存储空间:单链表的节点可以分散在内存的不同位置,通过指针连接起来,不需要连续的内存空间(数组需要连续的内存空间,当内存中没有足够大的连续空间时,数组就无法创建)。
2. 单链表的不足("链子" 的缺点)
- 随机访问效率低:要访问链表中的某个节点,必须从表头开始遍历,依次找到目标节点,时间复杂度是 O (n)(数组可以通过下标直接访问任意元素,时间复杂度是 O (1))。比如要访问链表的第 100 个节点,就需要从第一个节点开始,遍历 99 步才能找到。
- 额外的内存开销:每个节点都需要额外存储一个指针(指针域),用于指向 next 节点,这会增加内存开销(数组只需要存储数据,不需要额外的指针开销)。
- 实现复杂:相比于数组,单链表的实现需要定义结构体、处理指针、管理内存等,代码逻辑更复杂,容易出现指针错误(如野指针、空指针引用)和内存泄漏问题。
3. 单链表的适用场景
根据单链表的优势与不足,单链表适合以下场景:
- 数据量动态变化,无法预先确定数据规模(如日志记录、消息队列等)。
- 频繁进行插入、删除操作,且插入 / 删除位置主要在链表头部或中间(如栈、队列的实现,链表版的栈用头插法实现 push 和 pop,效率很高)。
- 内存空间碎片化,没有足够大的连续内存空间(如嵌入式系统、内存资源紧张的场景)。
而当需要频繁随机访问数据(如根据索引查找数据)、数据量固定且较小、对内存开销敏感时,数组会是更好的选择。
五、总结:从 "抽象" 到 "具体",掌握单链表的核心
通过本文的学习,我们从 "链子" 的形象比喻入手,将抽象的单链表概念转化为具体的 C 语言代码实现,逐步掌握了单链表的定义、初始化、插入、删除、遍历、内存释放等核心操作。回顾整个学习过程,我们可以总结出以下几个关键点:
- 单链表的本质是 "链式存储":单链表通过节点和指针将分散的数据串联起来,形成一条 "数据链子",每个节点包含数据域和指针域,指针域是连接各个节点的关键。
- 指针是单链表的 "灵魂":单链表的插入、删除等操作本质上都是指针的修改,理解指针的指向关系是掌握单链表的核心。在编写代码时,一定要理清指针的移动和指向变化,避免出现指针错误。
- 内存管理是单链表的 "重中之重":单链表的节点需要动态分配内存(malloc),使用完后必须释放内存(free),否则会造成内存泄漏。释放内存时要注意顺序,先暂存 next 节点,再释放当前节点。
- 结合生活比喻,化抽象为具体:单链表的概念比较抽象,但通过 "链子" 的比喻,我们可以很容易地理解节点的结构、链表的连接方式以及各种操作的逻辑。在学习其他数据结构时,也可以采用类似的方法,将抽象概念与生活中的具体事物联系起来,降低学习难度。
单链表是数据结构的基础,掌握了单链表,我们再学习双向链表、循环链表、链表版的栈和队列等更复杂的数据结构时,就会事半功倍。希望本文能够帮助大家真正理解单链表的核心原理和实现方法,为后续的数据结构学习打下坚实的基础。如果大家在学习过程中有任何疑问,欢迎在评论区留言讨论,我们一起进步!