1. 基本概念
1.1 神经网络
定义:
神经网络(neural network)是由具有适应性的简单单元组成的广泛并行互连的网络,它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应。
研究背景:
神经网络的研究由来已久,如今已发展成为一个庞大的、多学科交叉的领域。在机器学习中,神经网络学习(neural network learning)是机器学习与神经网络这两个学科领域的交叉部分。
基本组成:
神经网络中最基本的成分是神经元(neuron)模型,即上述定义中的"简单单元"。
1.2 神经元模型
生物学基础:
在生物神经网络中,每个神经元与其他神经元相连,当它"兴奋"时,就会向相连的神经元发送化学物质,从而改变这些神经元内的电位;如果某神经元的电位超过了一个"阈值"(threshold),那么它就会被激活,即"兴奋"起来,向其他神经元发送化学物质。
M-P神经元模型:
1943年,McCulloch和Pitts将上述情形抽象为图1所示的简单模型,这就是一直沿用至今的M-P神经元模型 。
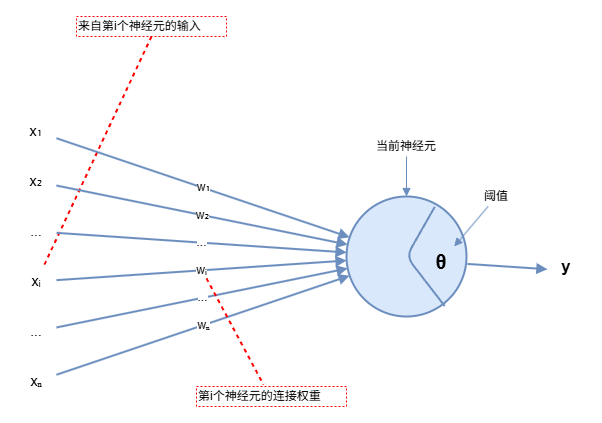
模型结构:
在这个模型中,神经元接收来自 n 个其他神经元传递过来的输入信号,这些输入信号通过带权重的连接(connection)进行传递,神经元接收到的总输入值将与神经元的阈值进行比较,然后通过激活函数(activation function)处理产生输出。
数学表示:
y=f(∑i=1nwixi−θ)y = f\left(\sum_{i=1}^{n} w_i x_i - \theta\right)y=f(i=1∑nwixi−θ)
其中 xix_ixi 表示来自第 i 个神经元的输入,wiw_iwi 表示第 i 个神经元的连接权重,θ 表示阈值,f 是激活函数。
1.3 激活函数
理想激活函数:
理想的激活函数是阶跃函数(step function),它将输入值映射为输出值"0"或"1"。显然"1"对应神经元兴奋,"0"对应神经元抑制。
阶跃函数的特点:
- 输出为0或1,对应神经元的抑制或兴奋
- 不连续、不光滑,不利于优化
Sigmoid函数:
由于阶跃函数具有不连续、不光滑等不太好的性质,因此实际常用Sigmoid函数作为激活函数。
Sigmoid函数的特点:
- 将可能在较大范围内变化的输入值挤压到 (0, 1) 输出值范围内,因此有时也称为"挤压函数"(squashing function)
- 连续、可微,便于优化
- 输出值在0到1之间,可以表示概率
数学表示:
sigmoid(x)=11+e−xsigmoid(x) = \frac{1}{1 + e^{-x}}sigmoid(x)=1+e−x1
2. 感知机与多层网络
2.1 感知机
定义:
感知机 (Perceptron)由两层神经元组成,如图2所示。
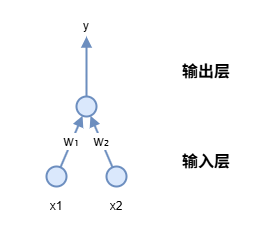
结构:
- 输入层:接收外界输入信号后传递给输出层
- 输出层:是M-P神经元,亦称"阈值逻辑单元"(threshold logic unit)
功能:
感知机能容易地实现逻辑"与"、"或"、"非"运算。
2.2 感知机学习规则
学习目标:
给定训练数据集,权重 wiw_iwi(i = 1, 2, ..., n)以及阈值 θ 可通过学习得到。
阈值处理:
阈值 θ 可看作一个固定输入为 -1.0 的"哑结点"(dummy node)所对应的连接权重 wn+1w_{n+1}wn+1,这样,权重和阈值的学习可统一为权重的学习。
学习规则:
对训练样例 (x, y),若当前感知机的输出为 ŷ,则感知机将这样调整权重:
wi←wi+Δwiw_i \leftarrow w_i + \Delta w_iwi←wi+Δwi
Δwi=η(y−y^)xi\Delta w_i = \eta(y - \hat{y})x_iΔwi=η(y−y^)xi
其中 η ∈ (0, 1) 称为学习率(learning rate)。
规则解释:
- 若感知机对训练样例
(x, y)预测正确,即ŷ = y,则感知机不发生变化 - 否则将根据错误的程度进行权重调整
2.3 感知机的局限性
线性可分问题:
感知机只有输出层神经元进行激活函数处理,即只拥有一层功能神经元(functional neuron),学习能力非常有限。事实上,上述"与"、"或"、"非"问题都是线性可分(linearly separable)的。
收敛性:
若两类模式是线性可分的,即存在一个线性超平面能将它们分开,则感知机的学习过程一定会收敛(converge)而求得适当的权向量 w=(w1;w2;...;wn+1)w = (w_1; w_2; ...; w_{n+1})w=(w1;w2;...;wn+1)。
非线性可分问题:
若两类模式不是线性可分的,则感知机的学习过程会发生振荡 (fluctuate),w 难以稳定下来,不能求得合适解。例如,感知机甚至不能解决异或(XOR)这样的简单非线性可分问题。
2.4 多层感知机
解决非线性问题:
要解决非线性可分问题,需考虑使用多层功能神经元。
隐藏层:
输入层与输出层之间的一层神经元,被称为隐藏层 (hidden layer)或隐层(hidden neuron),隐藏层和输出层神经元都是拥有激活函数的功能神经元。
多层前馈神经网络:
神经网络是每层神经元与下一层神经元全互连,神经元之间不存在同层连接,也不存在跨层连接。这样的神经网络结构通常称为多层前馈神经网络(multi-layer feedforward neural networks)。
网络结构:
- 输入层神经元:接收外界输入
- 隐藏层和输出层神经元:对信号进行加工,最终结果由输出层神经元输出
- 输入层神经元:仅接收输入,不进行函数处理
- 隐藏层和输出层:包含功能神经元
命名约定:
"两层网络"称为"单隐层网络"。只需包含隐层,即可称为多层网络。
学习过程:
神经网络的学习过程,就是根据训练数据来调整神经元之间的连接权 (connection weight)以及每个功能神经元的阈值;换言之,神经网络"学"到的东西,蕴涵在连接权与阈值中。
3. 总结
神经网络 是由具有适应性的简单单元组成的广泛并行互连的网络。M-P神经元模型是神经网络的基本组成单元,它接收来自其他神经元的输入信号,通过带权重的连接进行传递,与阈值比较后通过激活函数产生输出。
感知机 是最简单的神经网络,由两层神经元组成,能够实现逻辑"与"、"或"、"非"运算,但只能解决线性可分问题。对于非线性可分问题(如异或问题),需要使用多层感知机 或多层前馈神经网络。
多层前馈神经网络包含输入层、隐藏层和输出层,隐藏层和输出层包含功能神经元。神经网络的学习过程就是根据训练数据调整连接权和阈值。神经网络"学"到的东西蕴涵在连接权与阈值中。