机器学习 - K - 中心聚类

摘要：K-中心聚类算法通过选取代表性中心点进行聚类，相比K-均值对异常值更具鲁棒性。其实现步骤包括初始化中心点、分配数据点和迭代更新中心点。使用Python的scikit-learn库可快速实现该算法，其中KMedoids类支持自定义距离度量。虽然算法计算效率较高且支持非欧氏距离，但对簇数k的选择敏感，且在高维数据上性能受限。通过可视化可直观展示聚类结果，中心点以红色叉号标记。

[K - 中心聚类 - 算法](#K - 中心聚类 - 算法)

[Python 实现](#Python 实现)

示例

[K - 中心聚类 - 优势](#K - 中心聚类 - 优势)

[K - 中心聚类 - 劣势](#K - 中心聚类 - 劣势)

K - 中心聚类 - 算法

K - 中心聚类算法可总结如下：

初始化 k 个中心点 ------ 从数据集中随机选取 k 个数据点作为初始中心点。

将数据点分配至中心点 ------ 将每个数据点分配给距离其最近的中心点。

更新中心点 ------ 对于每个簇，选取能使该簇内所有其他数据点到其距离之和最小的数据点，将其设为新的中心点。

重复步骤 2 和步骤 3，直至算法收敛或达到最大迭代次数。

Python 实现

要在 Python 中实现 K - 中心聚类，我们可以使用 scikit-learn 库。该库提供了 KMedoids 类，可用于对数据集执行 K - 中心聚类。

首先，我们需要导入所需的库：

python 复制代码

from sklearn_extra.cluster import KMedoids
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

接下来，我们使用 scikit-learn 库中的 make_blobs() 函数生成一个样本数据集：

python 复制代码

X, y = make_blobs(n_samples=500, centers=3, random_state=42)

此处，我们生成一个包含 500 个数据点 和 3 个簇的数据集。

接下来，我们初始化 KMedoids 类并拟合数据：

python 复制代码

kmedoids = KMedoids(n_clusters=3, random_state=42)
kmedoids.fit(X)

此处，我们将簇的数量设为 3，并使用random_state参数来确保结果的可复现性。

最后，我们可以利用散点图将聚类结果可视化：

python 复制代码

plt.figure(figsize=(7.5, 3.5))
plt.scatter(X[:, 0], X[:, 1], c=kmedoids.labels_, cmap='viridis')
plt.scatter(kmedoids.cluster_centers_[:, 0],
kmedoids.cluster_centers_[:, 1], marker='x', color='red')
plt.show()

示例

以下是基于 Python 的完整实现代码：

python 复制代码

from sklearn_extra.cluster import KMedoids
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

# Generate sample data
X, y = make_blobs(n_samples=500, centers=3, random_state=42)

# Cluster the data using KMedoids
kmedoids = KMedoids(n_clusters=3, random_state=42)
kmedoids.fit(X)

# Plot the results
plt.figure(figsize=(7.5, 3.5))
plt.scatter(X[:, 0], X[:, 1], c=kmedoids.labels_, cmap='viridis')
plt.scatter(kmedoids.cluster_centers_[:, 0],
kmedoids.cluster_centers_[:, 1], marker='x', color='red')
plt.show()

输出

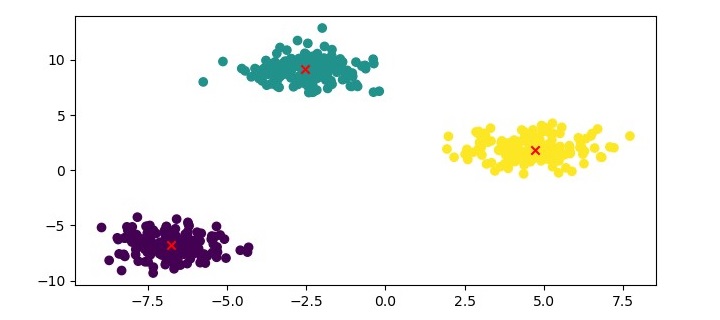
在此处，我们将数据点绘制成散点图，并根据其簇标签为数据点着色。同时，我们将中心点绘制成红色叉号。

K - 中心聚类 - 优势

K - 中心聚类算法的优势如下：

对异常值和噪声鲁棒性强 ------ 与 K - 均值聚类相比，K - 中心聚类对异常值和噪声的鲁棒性更强，因为它采用被称为中心点的代表性数据点来表征簇的中心。

可适配非欧氏距离度量 ------ K - 中心聚类能够兼容任意距离度量方式，包括曼哈顿距离、余弦相似度等非欧氏距离度量。

计算效率较高 ------ K - 中心聚类的计算复杂度为 \(O(k*n^2)\)，低于 K - 均值聚类的计算复杂度。

K - 中心聚类 - 劣势

K - 中心聚类算法的劣势如下：

对簇数量 k 的选择敏感 ------ K - 中心聚类的性能表现会受簇数量 k 的选择影响，对 k 值的设定较为敏感。

不适用于高维数据 ------ K - 中心聚类在高维数据上的表现可能不佳，因为高维场景下的中心点选取过程会产生较高的计算开销。