目录
[1. 初始化指针](#1. 初始化指针)
[2. 遍历原链表并分区](#2. 遍历原链表并分区)
[3. 处理边界情况和拼接链表](#3. 处理边界情况和拼接链表)
前言
上一篇文章讲解了双向链表概念与结构,实现双向链表(双向链表的初始化,双向链表的尾插,双向链表的头插,双向链表的尾删,双向链表的头删......),实现双向链表其余部分,顺序表与链表的分析,链表算法题 等知识的相关内容,接下来,链表算法题为本章节知识的内容。
一、链表算法题
1、链表的中间结点
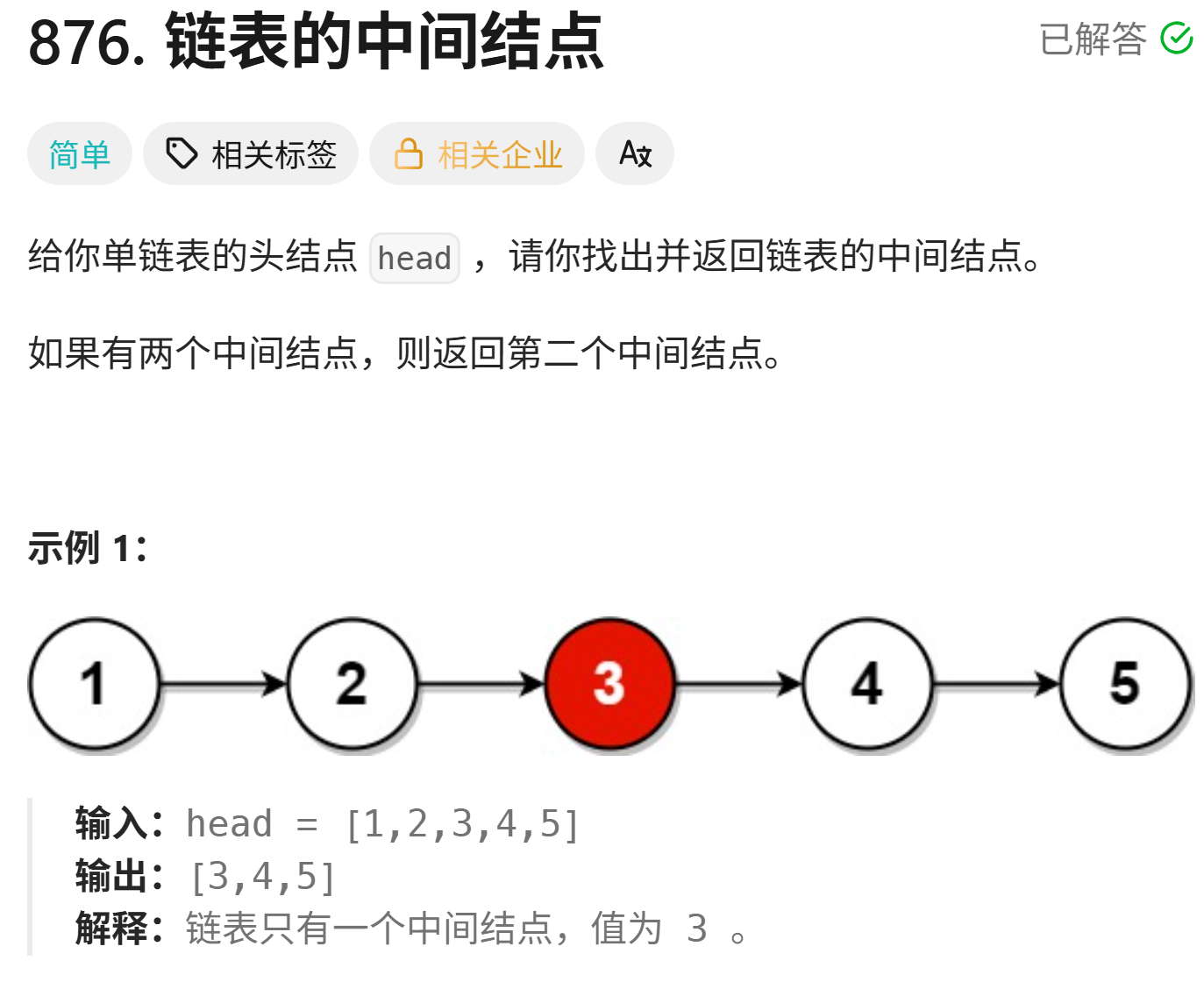
思路讲解:
单链表找中间节点算法解析:
单链表的节点通过指针串联,无法像数组一样通过索引直接访问中间元素,而我们要返回中间节点,简单来说:我们可以创建一个数组,来将每一个节点的值存入到数组中,通过一个临时变量记录节点个数,通过创建的临时变量来访问中间节点的值,但此方法很大的缺点:
- 空间复杂度与时间复杂度都很大,效率低
- 没有事先告知我们该链表有多少个节点,如果使用的为静态数组,空间开小了不行,开大了又会有空间浪费。
推荐解法:
通过 快慢指针法 高效定位单链表的中间节点,时间复杂度为 O(n) ,空间复杂度为 O(1),是链表操作中的经典技巧。
核心思路:快慢指针同步移动
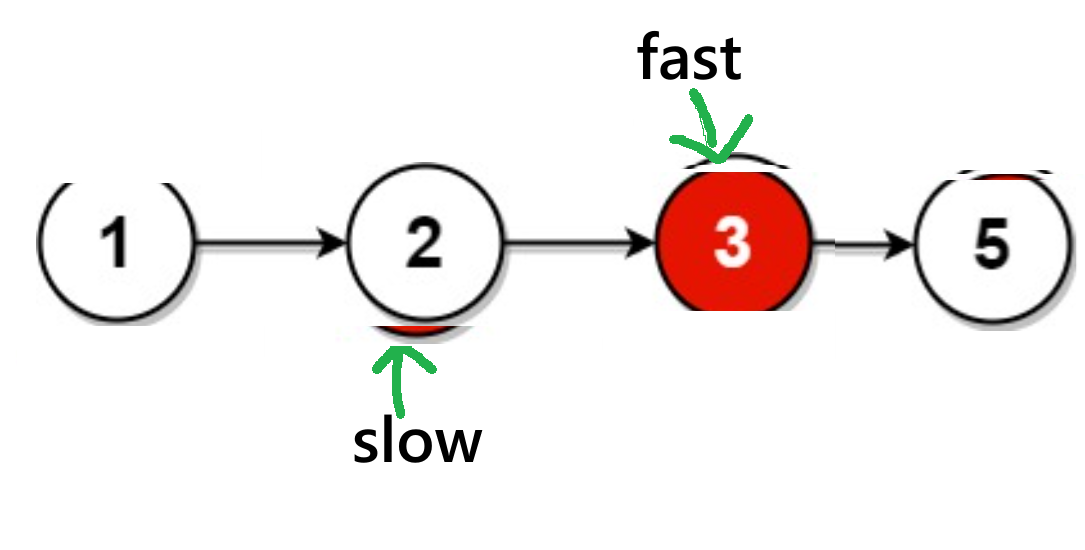
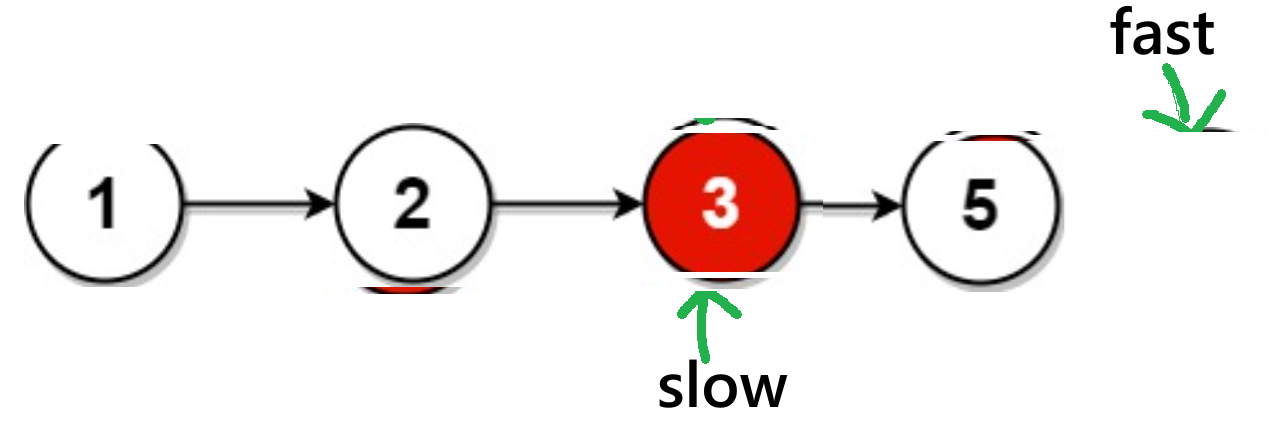
- 慢指针(slow) :每次移动 1 步。
- 快指针(fast) :每次移动 2 步。
- 终止条件 :当快指针无法继续移动(
fast == NULL或fast->next == NULL)时,慢指针恰好指向 中间节点。至于(
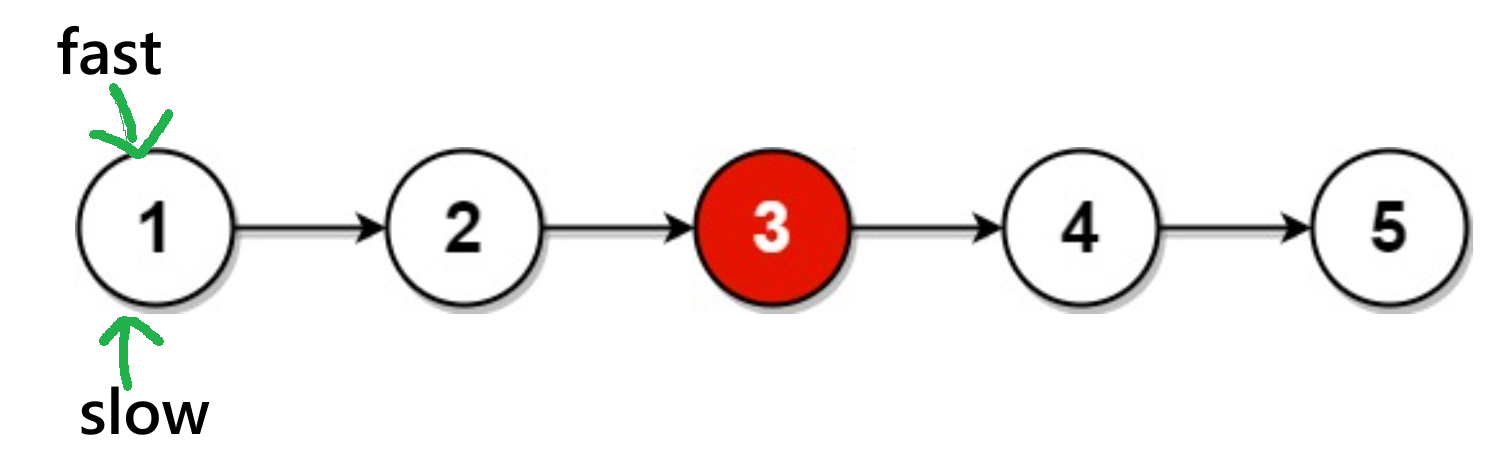
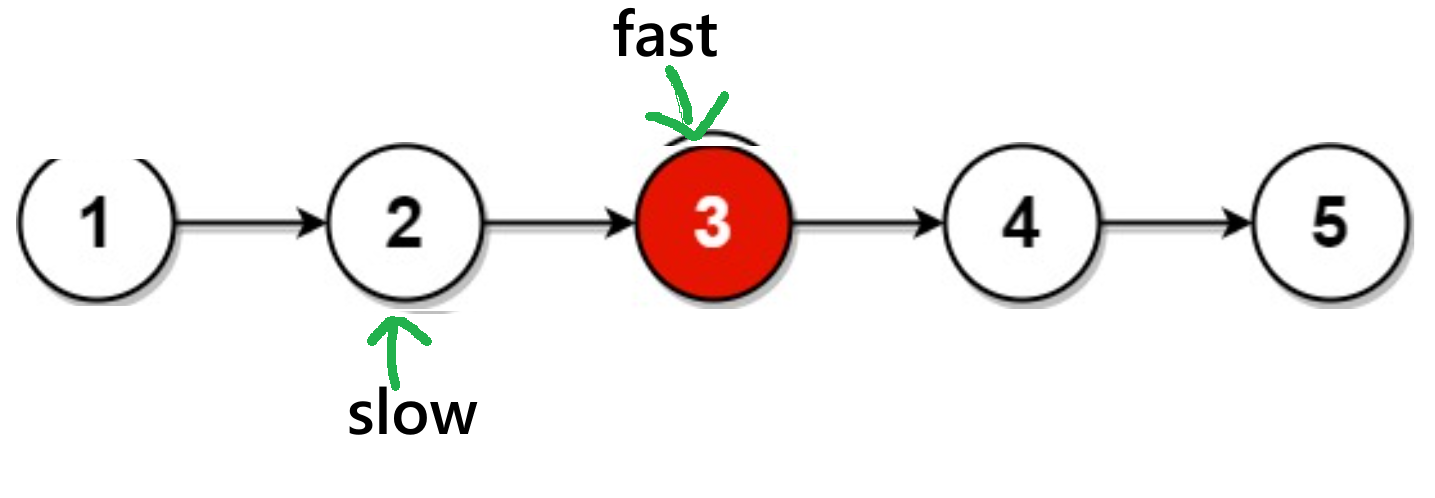
fast == NULL或fast->next == NULL)的情况,我以图来表示:情况1:
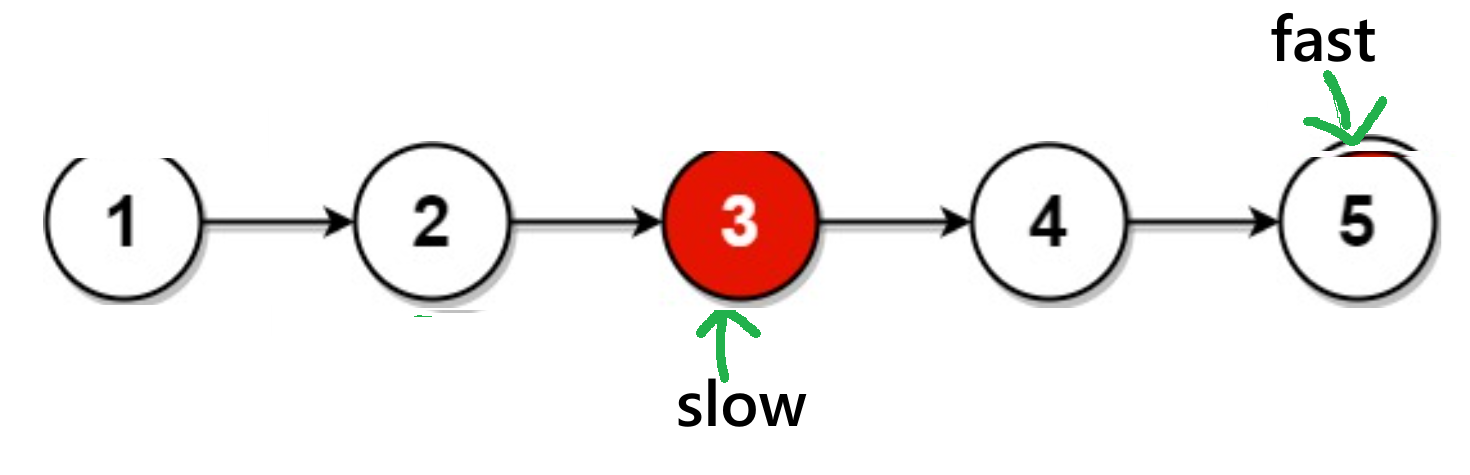
有奇数个节点:
此时为
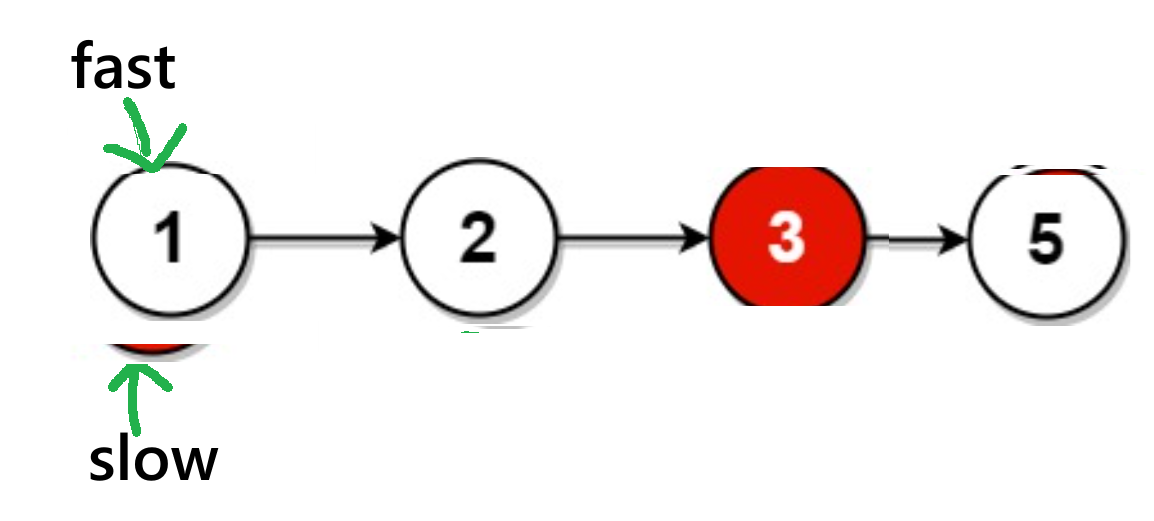
fast->next == NULL有偶数个节点:
通过图可知:此时为
fast= == NULL
所以我们的解决代码为:
cpp
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
typedef struct ListNode node;
struct ListNode* middleNode(struct ListNode* head)
{ node *fast=head;
node *slow=head;
while(fast&&fast->next)
{
fast=fast->next->next;
slow=slow->next;
}
return slow;
}
解题思路:
通过两个指针的步差关系,一次遍历即可定位中间节点。
cpp/** * Definition for singly-linked list. * struct ListNode { * int val; // 节点值 * struct ListNode *next; // 指向下一节点的指针 * }; */ typedef struct ListNode node; // 将结构体名简化为 node,简化后续代码书写 struct ListNode* middleNode(struct ListNode* head) { node *fast = head; // 快指针:初始指向头节点,每次走 2 步 node *slow = head; // 慢指针:初始指向头节点,每次走 1 步 // 循环条件:快指针未到链表尾部(需同时满足 fast 和 fast->next 非空) while (fast && fast->next) { fast = fast->next->next; // 快指针走 2 步 slow = slow->next; // 慢指针走 1 步 } return slow; // 慢指针指向中间节点 }
- 快指针(fast):每次移动 2 步,相当于"领跑者";
- 慢指针(slow):每次移动 1 步,相当于"追随者";
- 终止条件 :当快指针无法继续移动(
fast或fast->next为空)时,慢指针恰好走到链表中间。- 必须同时满足两个条件 :
fast != NULL:防止快指针本身为空(如链表只有 1 个节点时,fast->next会越界);fast->next != NULL:防止快指针下一步越界(如链表有 2 个节点时,fast->next->next会越界)。复杂度分析
- 时间复杂度:O(n),仅需遍历链表一次(快指针最多移动 n/2 步)。
- 空间复杂度:O(1),仅用两个指针变量(常数空间)。
2、两个升序链表合并为一个新的升序链表

思路讲解:
题目要求,我们将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
本题有多种方式实现:
- 我们可以创建一个新链表,通过这一个链表来进行操作,在新链表中进行操作。
解决代码:
cpp
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
typedef struct ListNode node;
struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2)
{
if(list1==NULL)
{
return list2;
}
if(list2==NULL)
{
return list1;
}
node* s1=list1;
node * s2=list2;
node * head=NULL;
node* tail=NULL;
while(s1&&s2)
{
if(s1->val<s2->val)
{
if(head==NULL)
{
head=s1;
tail=s1;
}
else
{
tail->next=s1;
tail=s1;
}
s1=s1->next;
}
else
{
if(head==NULL)
{
head=s2;
tail=s2;
}
else
{
tail->next=s2;
tail=s2;
}
s2=s2->next;
}
}
if(s1)
{
tail->next=s1;
}
if(s2)
{
tail->next=s2;
}
return head;
}
讲解:
函数定义与参数
cppstruct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2)
- 功能 :合并两个有序链表
list1和list2,返回合并后的新链表头节点。- 参数 :
list1和list2为待合并的有序单链表(非递减)。边界条件处理
cppif(list1==NULL) return list2; // 若list1为空,直接返回list2 if(list2==NULL) return list1; // 若list2为空,直接返回list1
- 作用:避免空链表导致的无效遍历,提升效率。
初始化指针
cppnode* s1 = list1; // 遍历list1的指针 node* s2 = list2; // 遍历list2的指针 node* head = NULL; // 合并后新链表的头节点 node* tail = NULL; // 合并后新链表的尾节点(用于链接新节点)核心合并逻辑(双指针遍历比较)
cppwhile(s1 && s2) { // 当s1和s2均未遍历完时循环 if(s1->val < s2->val) { // 若s1当前节点值更小 if(head == NULL) { // 首次链接节点(头节点未初始化) head = s1; // 头节点指向s1 tail = s1; // 尾节点指向s1 } else { tail->next = s1; // 尾节点的next指向s1(链接新节点) tail = s1; // 尾节点后移到s1 } s1 = s1->next; // s1指针后移,继续遍历list1 } else { // 若s2当前节点值更小或相等(非递减) // 逻辑同上,处理s2节点 if(head == NULL) { head = s2; tail = s2; } else { tail->next = s2; tail = s2; } s2 = s2->next; } }链接剩余节点
cppif(s1) tail->next = s1; // 若s1未遍历完,直接链接剩余节点 if(s2) tail->next = s2; // 若s2未遍历完,直接链接剩余节点
- 原因:循环结束后,至少有一个链表已遍历完,剩余节点本身有序,直接链接到新链表尾部即可。
返回结果
cppreturn head; // 返回合并后新链表的头节点总结
- 时间复杂度 :O(m+n)(m、n 为两链表长度),仅需一次遍历。
- 空间复杂度 :O(1),未创建新节点,仅通过指针操作合并。
- 优点:逻辑清晰,边界处理完善,适合理解合并链表的核心思路。
想 :每次比较
s1和s2指向的节点值,将较小的节点链接到新链表尾部,同时移动对应链表的遍历指针。
3、链表分割
由题意可知:
本题要求将值借助x分界,再将分界后的结果合并一起,题目要求,不可以改变数据顺序,我们可以通过,双链表法来实现:
- 创建两个链表,分别存储小于x、大于x的节点,最后将链表合并。
cpp
/*
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) : val(x), next(NULL) {}
};*/
class Partition
{
public:
ListNode* partition(ListNode* pHead, int x)
{
ListNode *h1=NULL,*t1=NULL;
ListNode *h2=NULL,*t2=NULL;
ListNode * p=pHead;
while(p)
{
if(p->val<x)
{
if(h1==NULL)
{
h1=p;
t1=p;
}
else
{
t1->next=p;
t1=p;
}
}
else
{
if(h2==NULL)
{
h2=p;
t2=p;
}
else
{
t2->next=p;
t2=p;
}
}
p=p->next;
}
if(t2)
{
t2->next=NULL;
}
if(t1)
{
t1->next=h2;
}
else if(t1==NULL&&h1==NULL&&h2)
{
return h2;
}
return h1;
}
};代码为C++代码,因为本题没有C提交的接口,但C++的语法兼容C,所以我们可以继续使用C语言知识,class类是以后讲解的内容。
讲解:
所有小于
x的节点在前,大于等于x的节点在后,且两部分内部节点顺序保持原链表顺序。以下是详细讲解:一、核心思路
- 定义两个子链表 :
h1/t1:存储 小于x的节点 (h1为头指针,t1为尾指针)。h2/t2:存储 大于等于x的节点 (h2为头指针,t2为尾指针)。- 遍历原链表 :
逐个节点判断值与x的关系,通过 尾插法 接入对应子链表(保持原顺序)。- 拼接两子链表 :
将h1子链表的尾部(t1->next)连接到h2子链表的头部(h2),并处理边界情况(如某一子链表为空)。二、代码逐段解析
1. 初始化指针
cppListNode *h1=NULL,*t1=NULL; // 小于 x 的链表:头指针h1,尾指针t1 ListNode *h2=NULL,*t2=NULL; // 大于等于 x 的链表:头指针h2,尾指针t2 ListNode *p=pHead; // 遍历原链表的指针
- 初始状态 :所有指针均为
NULL,表示两子链表为空。2. 遍历原链表并分区
cppwhile(p) { // 遍历原链表,p 为当前节点 if(p->val < x) { // 当前节点值 < x:接入 h1 子链表 if(h1 == NULL) { // h1 为空(首次插入) h1 = p; // h1 指向第一个节点 t1 = p; // t1 也指向该节点(尾指针初始化为头节点) } else { // h1 非空(后续插入) t1->next = p; // 尾指针 t1 的 next 指向新节点(尾插法) t1 = p; // t1 后移到新的尾部 } } else { // 当前节点值 >= x:接入 h2 子链表(逻辑同上) if(h2 == NULL) { h2 = p; t2 = p; } else { t2->next = p; t2 = p; } } p = p->next; // 遍历下一个节点 }
- 关键逻辑 :
- 尾插法 :通过
t1->next = p将新节点接在链表尾部,再移动t1到新尾部,确保子链表节点顺序与原链表一致。- 首次插入判断 :当子链表为空(
h1 == NULL或h2 == NULL)时,头指针和尾指针均指向当前节点;后续插入仅移动尾指针。3. 处理边界情况和拼接链表
cpp// ① 处理 h2 子链表的尾部:避免形成循环链表 if(t2) { // 若 h2 子链表非空(t2 不为 NULL) t2->next = NULL; // 将尾部节点的 next 置空(原链表可能有后续节点,需截断) } // ② 拼接 h1 和 h2 子链表 if(t1) { // 若 h1 子链表非空(t1 不为 NULL) t1->next = h2; // h1 尾部连接 h2 头部 } else if(t1 == NULL && h1 == NULL && h2) { // 若 h1 为空且 h2 非空 return h2; // 直接返回 h2(原链表所有节点均 >= x) } // ③ 返回结果:h1 为新链表头(若 h1 为空,返回 h2;h2 为空则返回 NULL) return h1;
- 核心操作 :
- 截断 h2 尾部 :
t2->next = NULL至关重要!若不处理,原链表中h2尾部节点的next可能指向h1中的节点,导致拼接后形成 循环链表。- 拼接逻辑 :
- 若
h1非空(t1 != NULL),直接拼接t1->next = h2;- 若
h1为空(所有节点均 >= x),则返回h2;- 若
h1和h2均为空(原链表为空),返回NULL(h1初始为NULL)。
4.链表回文结构
解题思路:
首先题目:
对于一个链表,请设计一个时间复杂度为O(n),额外空间复杂度为O(1)的算法,判断其是否为回文结构。
给定一个链表的头指针A,请返回一个bool值,代表其是否为回文结构。保证链表长度小于等于900。
我们看题目可以得知,链表的长度小于等于900,那么我们可以这样做:
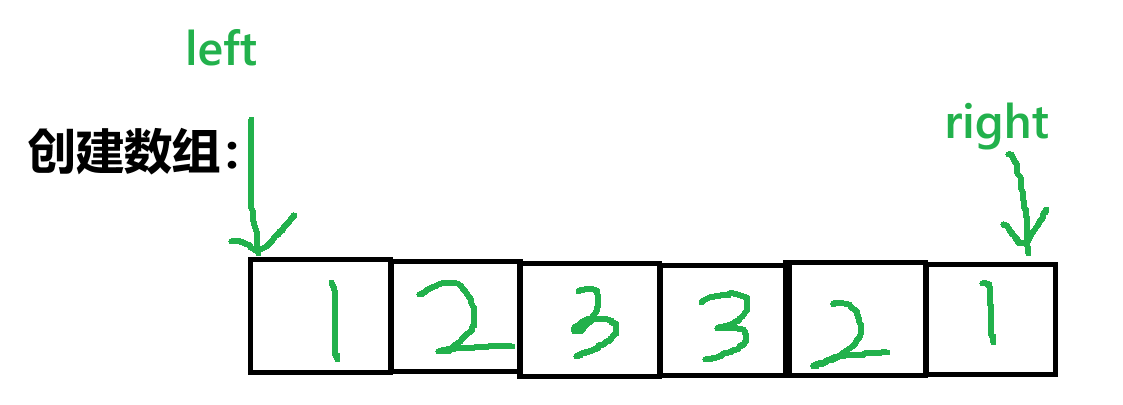
- 创建一个数组将所有值存储,最后再进行左右端的比较。
例:

cpp
/*
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) : val(x), next(NULL) {}
};*/
class PalindromeList
{
public:
bool hui(int *a,int left,int right)
{
while(left<right)
{
if(a[left]==a[right])
{
left++;
right--;
}
else
return false;
}
return true;
}
bool chkPalindrome(ListNode* A)
{
ListNode * p=A;
int node[900],i=0;
while(p)
{
node[i++]=p->val;
p=p->next;
}
return hui(node,0,i-1);
}
};讲解:
核心思路
- 链表转数组:遍历单链表,将所有节点值依次存入数组,将链表的"线性顺序"转换为数组的"随机访问"结构。
- 双指针验证回文 :使用两个指针分别从数组头部(
left=0)和尾部(right=i-1)向中间移动,逐位比较对应元素是否相等。若所有元素均相等,则为回文;否则不是。
cppbool hui(int *a, int left, int right) { while (left < right) { // 当左指针在右指针左侧时循环 if (a[left] == a[right]) { // 若当前左右元素相等 left++; // 左指针右移 right--; // 右指针左移 } else { // 若元素不相等,直接返回false(非回文) return false; } } return true; // 所有元素比较完毕且相等,返回true(回文) }思路简单,不过多说明了。
总结
以上就是今天要讲的内容,本篇文章涉及的知识点为:链表算法题的知识 的相关内容,为本章节知识的内容,希望大家能喜欢我的文章,谢谢各位,接下来的内容我会很快更新。我将更新链表算法题的进阶题和新知识。