算法基础篇：（十六）深度优先搜索（DFS）之递归型枚举与回溯剪枝初识

前言

在算法的世界里，搜索算法就像是一把万能钥匙，能帮我们打开各类问题的大门。而深度优先搜索（DFS），作为搜索家族中的核心成员，更是凭借其 "一条路走到黑，走不通再回头" 的特性，成为解决枚举、组合、排列等问题的利器。今天，我们就聚焦于DFS 的递归型枚举 ，并聊聊回溯与剪枝这两个让 DFS 效率倍增的关键技巧，通过具体的例题一步步拆解，带你走进 DFS 的奇妙世界。下面就让我们正式开始吧！

一、搜索的本质：从暴搜到 DFS

在正式讲解 DFS 之前，我们先搞清楚一个基础问题：什么是搜索？

简单来说，搜索就是一种枚举策略，通过穷举所有可能的情况，找到问题的最优解或者统计合法解的个数。因为要 "穷举"，所以搜索也常被戏称为 "暴搜"。而搜索主要分为两大分支：深度优先搜索（DFS）和宽度优先搜索（BFS）。本文的主角，就是 DFS。

这里还要区分两个容易混淆的概念：遍历和搜索。遍历是形式，是 "走过所有节点" 的动作；搜索是目的，是 "找到目标解" 的过程。在实际应用中，我们通常不会严格区分二者，把 DFS 遍历当作 DFS 搜索来处理即可。

而 DFS 之所以能高效解决枚举问题，离不开两个核心操作：回溯和剪枝。

回溯：当搜索到某一步发现走不通，或者已经走到路径的尽头时，就退回上一步重新选择，这就像走迷宫时发现死胡同，掉头回到上一个岔路口。

剪枝：在搜索过程中，提前砍掉那些重复、无效或者不可能得到最优解的分支，减少不必要的计算，就像修剪树木一样，去掉多余的枝叶，让能量集中在有用的枝干上。

接下来，我们将通过枚举子集 、组合型枚举 、枚举排列 和全排列四个经典问题，手把手教你用 DFS 实现递归型枚举，同时理解回溯与剪枝的实际应用。

二、枚举子集：从 N 个元素中选任意个

题目链接如下：https://www.luogu.com.cn/problem/B3622

2.1 问题描述

这是洛谷的经典入门题B3622 枚举子集（递归实现指数型枚举），题目大意是：给定 n 位同学，从中选出任意名同学参加合唱，输出所有可能的选择方案。每个方案用字符串表示，第 i 位为 Y 表示第 i 名同学参加，为 N 表示不参加，结果按字典序输出。

比如输入 n=3 时，输出是：

复制代码

NNN
NNY
NYN
NYY
YNN
YNY
YYN
YYY

2.2 思路分析：画决策树，找重复子问题

解决 DFS 问题的第一步，往往是画决策树。决策树能直观地展示出每一步的选择，帮我们找到重复的子问题。

对于 n=3 的情况，我们从第一个同学开始，每一步都有两个选择：选（Y）或不选（N）。决策树如下：

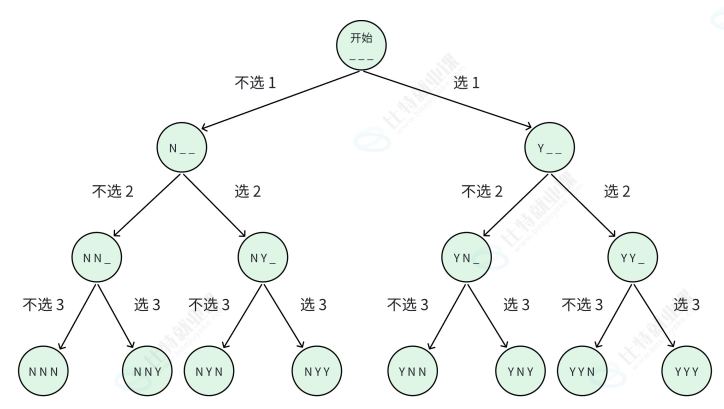
从决策树中能清晰看到，重复的子问题是：对第 pos 位同学，选择选或不选。而要保证字典序输出，我们需要先考虑 "不选"，再考虑 "选"。

接下来就是用递归实现这个决策过程：

递归函数的参数：pos表示当前处理到第几位同学。

递归终止条件：当pos > n时，说明已经处理完所有同学，此时输出当前的选择方案。

递归过程：先执行 "不选" 操作，将 'N' 加入路径，递归处理下一位；再执行 "选" 操作，将 'Y' 加入路径，递归处理下一位。

回溯操作：递归返回后，要把路径中最后加入的字符删除，恢复现场，为下一次选择做准备。

2.3 代码实现

cpp 复制代码

#include <iostream>
#include <string>
using namespace std;

int n;
string path; // 记录递归过程中的决策路径

void dfs(int pos) {
    // 递归终止：处理完所有同学
    if (pos > n) {
        cout << path << endl;
        return;
    }

    // 第一步：不选当前同学
    path += 'N';
    dfs(pos + 1);
    path.pop_back(); // 回溯，删除最后一个字符

    // 第二步：选当前同学
    path += 'Y';
    dfs(pos + 1);
    path.pop_back(); // 回溯，恢复现场
}

int main() {
    cin >> n;
    dfs(1); // 从第1位同学开始处理
    return 0;
}

2.4 代码解析

path 变量：用来记录每一步的选择，是 "路径" 的核心载体。

回溯的关键 ：**path.pop_back()**是整个代码的灵魂。因为递归调用后，path 会保留上一次的选择，必须删除最后一个字符，才能让下一次选择不受影响。比如处理完 "不选 1" 的所有情况后，要把 'N' 删掉，才能开始处理 "选 1" 的情况。

字典序保证：先处理 "不选" 再处理 "选"，正好对应字典序中 N 在 Y 前面的规则。

三、组合型枚举：从 N 个元素中选 M 个

题目链接：https://www.luogu.com.cn/problem/P10448

3.1 问题描述

洛谷题目P10448 组合型枚举要求：从 1~n 这 n 个整数中随机选出 m 个，按字典序输出所有可能的组合方案。同一行内的数升序排列，不同行按字典序排序。

比如输入 n=5，m=3 时，输出是：

复制代码

3.2 思路分析：决策树与剪枝

组合问题和子集问题的区别在于：组合要求选固定数量的元素，且不考虑顺序（比如 1 2 3 和 3 2 1 是同一个组合）。

我们以 n=4，m=3 为例画决策树：

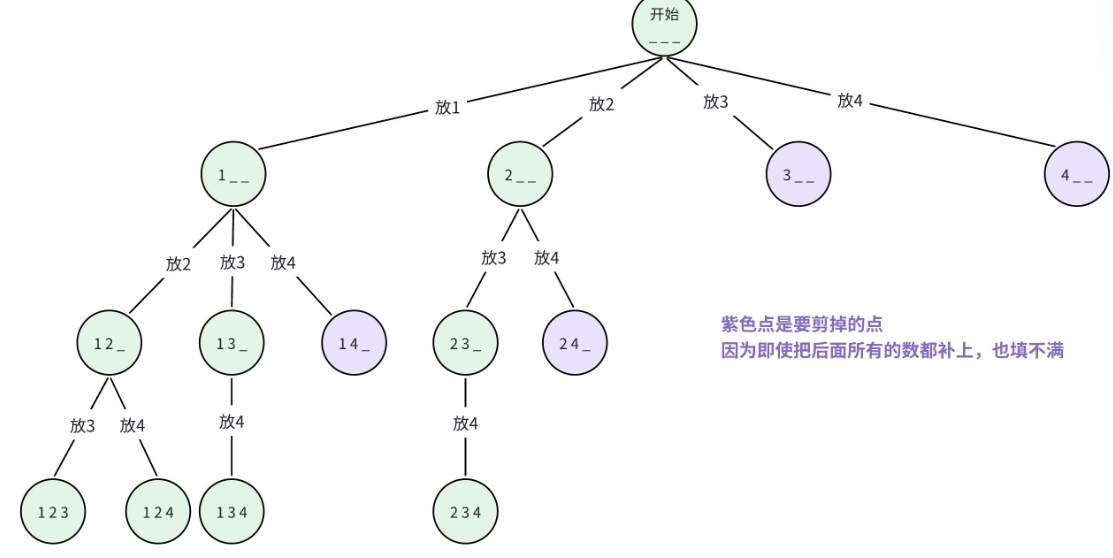
这里的重复子问题是：当前位置要放的数，必须是上一个数的下一位 （保证升序，避免重复组合）。同时，我们能看到决策树中有一些 "无效分支"，比如选了 3 之后，剩下的数只有 4，无法凑够 3 个元素，这些分支可以提前剪掉，这就是剪枝的思想。

递归函数的设计要点：

参数：begin表示当前选择的数从哪个数开始（避免重复），path记录已选的数。

终止条件：当path.size() == m时，输出组合方案。

递归过程：从begin到 n 遍历数，将当前数加入 path，递归处理下一个位置（起始数为i+1）。

回溯：递归返回后，删除 path中最后一个数。

3.3 代码实现

cpp 复制代码

#include <iostream>
#include <vector>
using namespace std;

int n, m;
vector<int> path; // 记录组合的路径

void dfs(int begin) {
    // 递归终止：选够了m个数
    if (path.size() == m) {
        for (auto x : path) {
            cout << x << " ";
        }
        cout << endl;
        return;
    }

    // 从begin开始枚举，避免重复组合
    for (int i = begin; i <= n; i++) {
        path.push_back(i);
        dfs(i + 1); // 下一个数从i+1开始
        path.pop_back(); // 回溯
    }
}

int main() {
    cin >> n >> m;
    dfs(1); // 从1开始选
    return 0;
}

3.4 剪枝优化

在上面的代码中，其实还有优化空间。比如当剩下的数的数量小于 "还需要选的数的数量" 时，就没必要继续搜索了。比如 n=5，m=3，当我们选到 4 的时候，还需要选 2 个数，但剩下的数只有 5，显然无法满足，这时候可以直接剪枝。

优化后的代码（添加剪枝条件）：

cpp 复制代码

#include <iostream>
#include <vector>
using namespace std;

int n, m;
vector<int> path;

void dfs(int begin) {
    if (path.size() == m) {
        for (auto x : path) {
            cout << x << " ";
        }
        cout << endl;
        return;
    }

    // 剪枝：剩下的数不够选，直接退出
    // 还需要选的数：m - path.size()
    // 剩下的数：n - i + 1
    for (int i = begin; i <= n - (m - path.size()) + 1; i++) {
        path.push_back(i);
        dfs(i + 1);
        path.pop_back();
    }
}

int main() {
    cin >> n >> m;
    dfs(1);
    return 0;
}

这个剪枝条件能大幅减少递归的次数，尤其是当 n 和 m 较大时，效率提升非常明显。

四、枚举排列：从 N 个元素中选 K 个排列

题目链接如下：https://www.luogu.com.cn/problem/B3623

4.1 问题描述

洛谷题目B3623 枚举排列（递归实现排列型枚举）要求：给定 n 名学生，选出 k 人排成一列拍照，按字典序输出所有可能的排列方式。

比如输入 n=3，k=2 时，输出是：

复制代码

4.2 思路分析：排列的去重剪枝

排列问题和组合问题的核心区别是：排列考虑顺序，组合不考虑顺序 。因此，排列的决策树需要考虑 "选过的数不能再选"，这就需要一个标记数组来记录哪些数已经被选过，这也是一种剪枝。

以 n=3，k=2 为例画决策树：

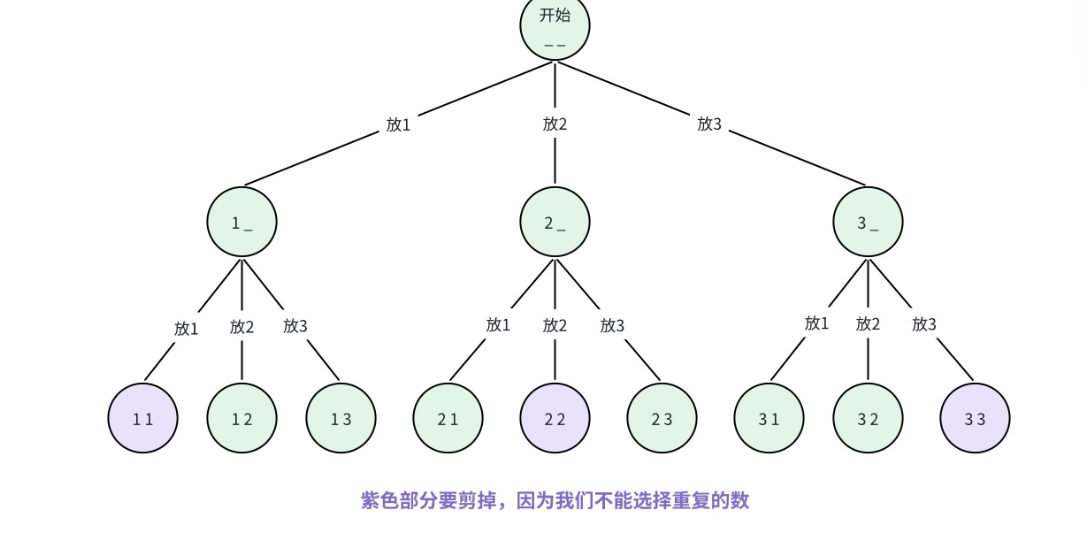
其中，紫色的分支（选过的数再次被选）需要剪掉，比如选了 1 之后，不能再选 1，因此 1 下面的 1 分支要剪掉。

递归函数的设计要点：

参数：不需要begin，而是用st数组标记数是否被选过，path记录排列的路径。

终止条件：path.size() == k时，输出排列方案。

递归过程：从 1 到 n 遍历数，如果数未被选过，标记为已选，加入 path，递归处理下一个位置。

回溯：递归返回后，取消标记，删除 path中最后一个数。

4.3 代码实现

cpp 复制代码

#include <iostream>
#include <vector>
using namespace std;

const int N = 15;
int n, k;
vector<int> path;
bool st[N]; // 标记数是否被选过

void dfs() {
    // 递归终止：选够了k个数
    if (path.size() == k) {
        for (auto x : path) {
            cout << x << " ";
        }
        cout << endl;
        return;
    }

    // 从1到n枚举所有数
    for (int i = 1; i <= n; i++) {
        if (st[i]) continue; // 剪枝：跳过已选的数
        st[i] = true; // 标记为已选
        path.push_back(i);
        dfs();
        // 回溯：取消标记，删除最后一个数
        st[i] = false;
        path.pop_back();
    }
}

int main() {
    cin >> n >> k;
    dfs();
    return 0;
}

4.4 代码解析

st 数组：是排列问题的核心，通过标记已选的数，避免重复选择，实现剪枝。

回溯的完整性 ：不仅要删除 path中的数，还要把 st数组的标记恢复为 false，否则会影响后续的选择。比如选了 1 之后，递归返回时必须把 st [1] 设为 false，才能让后面的分支再次选择 1。

五、全排列问题：N 个元素的全排列

题目链接如下：https://www.luogu.com.cn/problem/P1706

5.1 问题描述

洛谷题目P1706 全排列问题要求：按字典序输出自然数 1 到 n 的所有不重复的排列，每个数字占 5 个场宽。

比如输入 n=3 时，输出是：

复制代码

    1    2    3
    1    3    2
    2    1    3
    2    3    1
    3    1    2
    3    2    1

5.2 思路分析：排列问题的特例

全排列是排列问题的特例，即k=n 的情况。因此，递归的思路和枚举排列基本一致，只是终止条件变为path.size() == n。

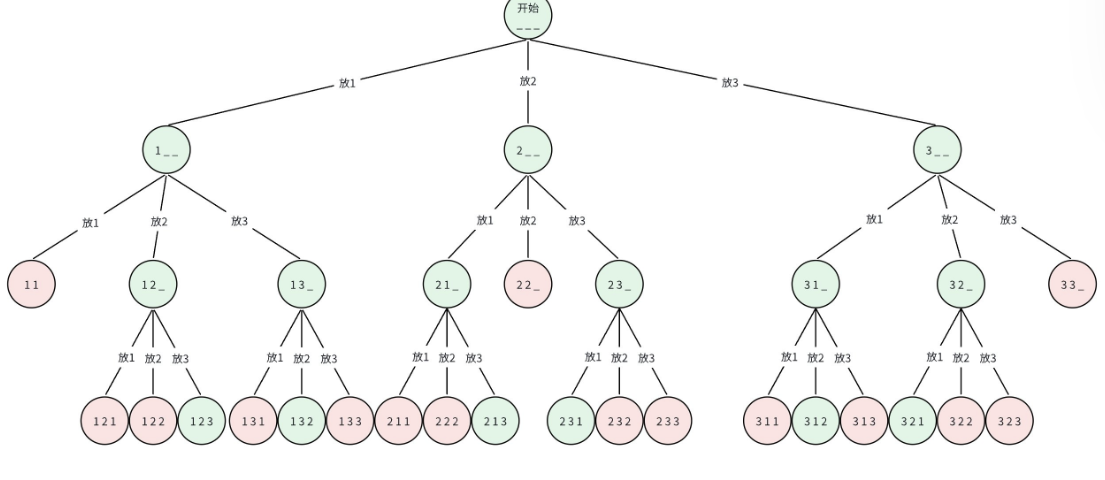
另外，C++ 的 STL 中提供了next_permutation函数，可以直接生成全排列，但作为学习 DFS 的过程，我们还是要掌握手动实现的方法。

5.3 代码实现

cpp 复制代码

#include <iostream>
#include <vector>
using namespace std;

const int N = 15;
int n;
vector<int> path;
bool st[N]; // 标记数是否被选过

void dfs() {
    // 递归终止：选够了n个数（全排列）
    if (path.size() == n) {
        for (auto x : path) {
            printf("%5d", x); // 每个数字占5个场宽
        }
        cout << endl;
        return;
    }

    for (int i = 1; i <= n; i++) {
        if (st[i]) continue; // 剪枝：跳过已选的数
        st[i] = true;
        path.push_back(i);
        dfs();
        // 回溯
        st[i] = false;
        path.pop_back();
    }
}

int main() {
    cin >> n;
    dfs();
    return 0;
}

5.4 STL 函数实现（拓展）

如果想快速实现全排列，可以使用next_permutation函数，代码如下：

cpp 复制代码

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

int main() {
    int n;
    cin >> n;
    vector<int> arr(n);
    for (int i = 0; i < n; i++) {
        arr[i] = i + 1;
    }
    do {
        for (auto x : arr) {
            printf("%5d", x);
        }
        cout << endl;
    } while (next_permutation(arr.begin(), arr.end()));
    return 0;
}

next_permutation会自动生成下一个字典序的排列，直到没有下一个排列为止。但需要注意的是，使用该函数前，数组必须是有序的，否则会从当前排列开始生成。

六、回溯与剪枝的核心思想总结

通过上面四个例题，我们已经掌握了 DFS 递归型枚举的基本方法，也初步接触了回溯和剪枝。这里总结一下核心要点：

6.1 回溯的本质

回溯是 "试错" 的过程：在递归中做出选择，若发现选择无效，就撤销选择，回到上一步重新选择。回溯的关键是恢复现场，比如删除 path 中的最后一个元素、取消 st 数组的标记等。没有恢复现场，递归就会陷入混乱，因为上一次的选择会影响后续的决策。

6.2 剪枝的常见类型

在 DFS 中，剪枝是提升效率的关键，常见的剪枝类型有：

可行性剪枝：比如组合问题中，剩下的数不够选就直接退出；排列问题中，跳过已选的数。

最优性剪枝：在求最优解的问题中，如果当前路径的代价已经超过已知的最优解，就停止搜索该分支。

重复性剪枝：避免搜索重复的状态，比如排列问题中的 st 数组标记。

6.3 DFS 递归型枚举的通用步骤

解决这类问题，我们可以遵循一个固定的套路：

画决策树：把每一步的选择可视化，找到重复子问题。

设计递归函数：确定参数、终止条件、递归过程。

实现递归与回溯：在递归中做出选择，递归返回后恢复现场。

添加剪枝：识别无效分支，提前退出，减少计算量。

总结

在实际应用中，DFS 的递归型枚举还可以结合更多技巧，比如记忆化搜索 （将已经计算过的状态保存起来，避免重复计算）、状态压缩（用二进制数表示状态）等。后续我们会继续讲解这些进阶技巧，让你的 DFS 功力更上一层楼。

最后，送给大家一句话：DFS 的核心是 "敢想敢写"，先画出决策树，再一步步实现，回溯和剪枝都是在这个基础上的优化。希望大家多动手敲代码，多尝试不同的问题，真正掌握 DFS 的精髓！

算法基础篇：（十六）深度优先搜索（DFS）之递归型枚举与回溯剪枝初识

目录

前言

一、搜索的本质：从暴搜到 DFS

二、枚举子集：从 N 个元素中选任意个

2.1 问题描述

2.2 思路分析：画决策树，找重复子问题

2.3 代码实现

2.4 代码解析

三、组合型枚举：从 N 个元素中选 M 个

3.1 问题描述

3.2 思路分析：决策树与剪枝

3.3 代码实现

3.4 剪枝优化

四、枚举排列：从 N 个元素中选 K 个排列

4.1 问题描述

4.2 思路分析：排列的去重剪枝

4.3 代码实现

4.4 代码解析

五、全排列问题：N 个元素的全排列

5.1 问题描述

5.2 思路分析：排列问题的特例

5.3 代码实现

5.4 STL 函数实现（拓展）

六、回溯与剪枝的核心思想总结

6.1 回溯的本质

6.2 剪枝的常见类型

6.3 DFS 递归型枚举的通用步骤

总结