本文档聚焦空间填充曲线的核心原理、类型、实现方法及应用场景,核心是解决空间数据(n 维)向一维数据的映射问题,以重用关系数据库的物理存储和索引模型。
一、空间填充曲线的核心定位与价值
1. 核心目标
- 将无序的 n 维空间数据转换为有序的一维数据,适配关系数据库的现有架构。
- 实现空间数据的聚集存储,减少查询时的 I/O 开销,提升空间相关查询(如范围查询、邻近查询)效率。
2. 核心优势(重用关系数据库能力)
- 重用数据文件组织方式:堆文件、有序文件、哈希文件(聚集存储)。
- 重用数值索引结构:B + 树、哈希表,无需重构数据库底层机制。
3. 基本特性
- 一条连续且无交叉的曲线,能遍历并填充均匀网格组成的四边形。
- 采用 m 阶递归生成:m 阶曲线的每个网格由 m-1 阶曲线填充,实现空间的循环分解。
二、空间填充曲线的基础问题与解决方案
1. 关键问题与核心思路
| 问题 | 解答 |
|---|---|
| 为何要将 n 维空间数据转为 1 维? | 适配 B + 树等成熟一维索引结构,利用现有数据库查询优化能力 |
| 如何实现 n 维到 1 维的映射? | 假设有限粒度(如 2³²×2³² 网格),通过曲线遍历规则分配一维编号 |
| 传统映射方式(如行优先、蛇形曲线)的缺陷? | 无法保持空间邻近性(一维编号相邻的点,空间位置可能很远),聚集效果差 |
2. 核心解决方案
- 采用 Z 曲线(Z-Curve)或希尔伯特曲线(Hilbert Curve),通过特殊的遍历规则减少 "长跳跃",优先填满一个象限再移动,提升空间邻近性保留能力。
三、两种核心空间填充曲线详解
1. Z 曲线(Z-Curve)
(1)定义与形态
- 一种通过位交错(bit-shuffling)生成的空间填充曲线,遍历路径呈 "Z" 或 "N" 形,递归扩展。
- 映射逻辑:优先按 y 坐标、后按 x 坐标的位进行交错组合(N 曲线相反,先 x 后 y)。
(2)生成方法
- 递归法:以 1 阶 "Z" 形为基础,高阶曲线通过在低阶曲线的每个网格中嵌入同形低阶曲线生成。
- 位交错法:将 x、y 坐标的二进制位按 "y 位 - x 位" 的顺序交替拼接,形成一维 z 值(例:x=0010₂、y=0100₂,交错后为 010000₂=24)。
- 线性四叉树法:为四叉树的每个象限分配二进制标识(如 W=0、E=1、N=1、S=0),组合标识得到 z 值(例:WN=0101₂=5)。
(3)反向映射
- 已知 z 值时,通过拆分交错的二进制位,分别提取 x、y 坐标的二进制信息,还原空间位置。
2. 希尔伯特曲线(Hilbert Curve)
(1)定义与形态
- 更复杂的空间填充曲线,通过旋转和反射递归生成,无交叉且空间邻近性保留能力更强。
- 生成特点:需处理旋转逻辑,高阶曲线由低阶曲线经旋转、反射后拼接而成(例:2 阶曲线由 4 个 1 阶曲线旋转组合)。
(2)(X,Y) 到希尔伯特值的转换步骤
- 输入 n 位二进制表示的 x、y 坐标。
- 交错 x、y 的二进制位,形成字符串 S。
- 将 S 拆分为 2 位一组的数组。
- 按规则转换 2 位组:"00"=0、"01"=1、"10"=3、"11"=2。
- 旋转 / 反射调整:从左到右扫描数组,j=0 时交换后续 1 和 3,j=3 时交换后续 0 和 2。
- 将调整后的数组项转回二进制,组合计算十进制希尔伯特值。
(3)示例验证
- 例 1:X=001₂、Y=000₂ → 交错后 000010 → 分组 [00,00,10] → 转换 [0,0,3] → 调整后 [0,0,1] → 二进制 000011 → 十进制 3。
- 例 2:X=100₂、Y=001₂ → 交错后 100001 → 分组 [10,00,01] → 转换 [3,0,1] → 调整后 [3,2,1] → 二进制 111001 → 十进制 57。
3. Z 曲线与希尔伯特曲线对比
| 特性 | Z 曲线 | 希尔伯特曲线 |
|---|---|---|
| 空间聚集性 | 较差,可能出现 "长跳跃" | 更优,空间邻近点的一维编号更集中 |
| 映射复杂度 | 简单(位交错 / 递归逻辑直观) | 复杂(需处理旋转、反射) |
| 核心优势 | 实现成本低,适配简单场景 | 查询效率更高(减少 I/O 开销) |
| 共同缺陷 | 均无法完全保证空间邻近性(一维编号相邻≠空间位置相邻) | 均无法完全保证空间邻近性 |
四、空间填充曲线的存储与查询算法
1. 磁盘存储方式
(1)无 B + 树的有序存储
- 按 z 值 / H 值对数据排序后存储,查询时通过二分查找定位目标值。
- 优势:实现简单;劣势:范围查询、动态更新效率低。
(2)带 B + 树的有序存储(推荐)
- 将 z 值 / H 值作为索引键构建 B + 树,数据按 z 值 / H 值有序存储。
- 核心优势:复用商用数据库内置 B + 树能力,支持并发控制与故障恢复,适配 OLTP 场景。
2. 核心查询场景实现
(1)点查询
- 步骤:计算目标点的 z 值 / H 值 → 通过二分查找(无 B + 树)或 B + 树查询定位对应数据。
- 示例:查找 (0,3) 对应的城市 → 计算 z 值 → 检索 B + 树获取记录。
(2)范围查询
- 步骤:将空间范围转换为多个连续的 z 值 / H 值区间 → 利用 B + 树定位区间起始值 → 遍历有序数据获取所有符合条件的记录。
- 优化策略:合并相邻区间(如 9、11-15 合并为 8-15),减少查询次数;按四叉树方式递归分解非满区间,精准匹配范围。
(3)k 近邻查询(k-nn)
- 步骤:计算目标点的 z 值 / H 值 → 通过 B + 树找到一维空间中的邻近 z 值 → 扩展为空间范围 → 执行范围查询获取 k 个空间邻近点。
(4)空间连接查询
- 场景:查找空间上相交 / 邻近的对象对(如 "与湖泊相交的县")。
- 算法:基于 z 值 / H 值排序的合并连接(Merge Join) → 利用前缀属性(z2 是 z1 的前缀则 z2 对应的区域包含 z1 区域)匹配对象 → 去重后返回结果。
- 优势:复杂度远低于暴力算法 O (N×M),效率显著提升。
3. 区域数据的处理
(1)区域的 z 值表示
- 通过四叉树分解区域,每个子区域对应一个 z 值(含 "*" 通配符,代表 "不关心" 位),一个区域可能对应多个 z 值(例:区域 C 对应 z 值 0010、1000)。
(2)区域查询规则
- 前缀匹配原则:若 z2 是 z1 的前缀,则 z2 对应的区域完全包含 z1 对应的区域;否则为不相交或部分相交。
- 示例:z1=011001**,z2=01******* → z2 是 z1 的前缀,故 z2 包含 z1;z3=0100*** 与 z1 无前缀关系,故不相交。
五、空间填充曲线小结
1. 核心逻辑
- 本质:通过 Z 曲线 / 希尔伯特曲线实现 n 维空间数据到 1 维数据的映射,重用关系数据库的存储和索引模型。
- 核心价值:提升空间数据查询的 I/O 效率,适配现有数据库架构,降低开发成本。
2. 关键应用场景
- 点查询、范围查询、k 近邻查询、空间连接查询,适用于空间数据库中的 POI 检索、区域分析等场景。
3. 后续延伸
- 空间填充曲线是空间索引的基础,后续将基于此展开网格索引、四叉树索引、R 树索引等专用空间索引技术。
空间填充曲线查询算法步骤流程图
该流程图基于文档中空间填充曲线的存储逻辑与查询规则,拆解点查询、范围查询、k 近邻查询、空间连接查询的核心执行步骤,直观呈现 "空间→一维→空间" 的映射与查询闭环。
一、点查询流程图(以 Z 曲线 + B + 树为例)
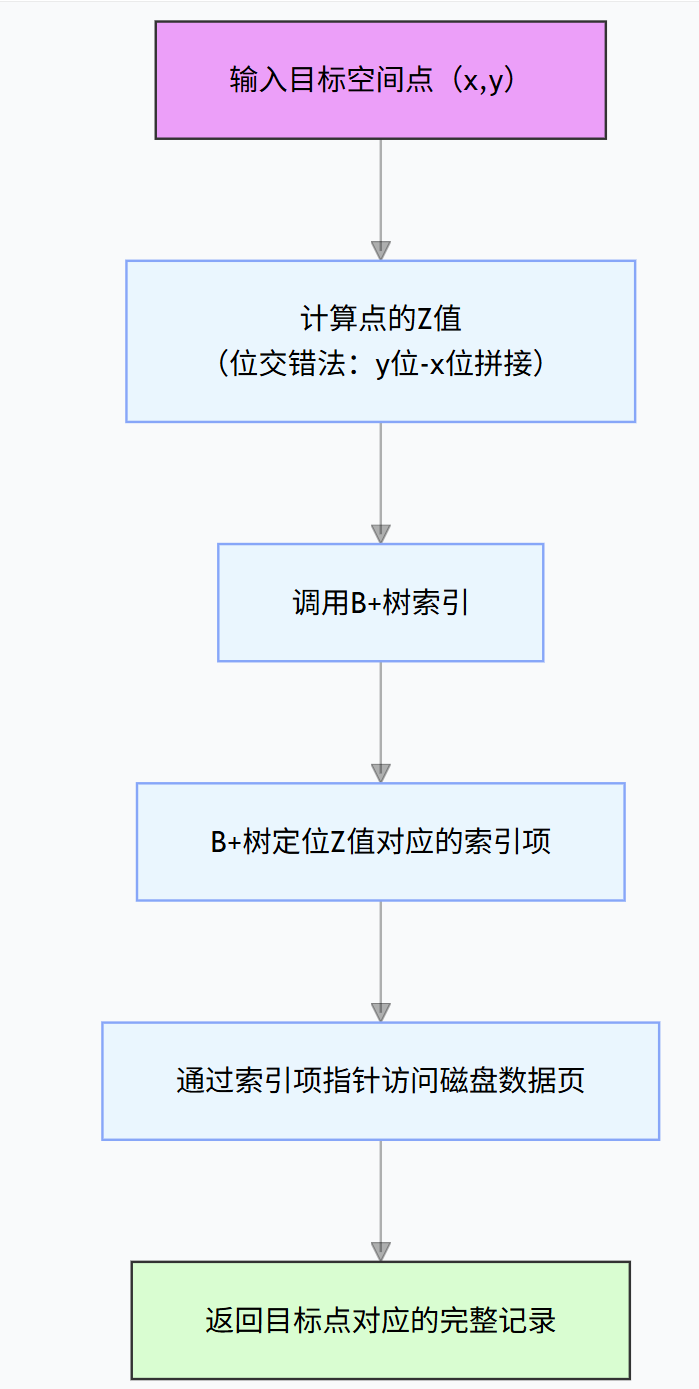
核心说明:无 B + 树时,可将步骤 C-D 替换为 "对有序存储的 Z 值列表执行二分查找",本质是通过一维值定位空间数据。
二、范围查询流程图(以希尔伯特曲线为例)
flowchart TD
A[输入空间查询范围<br>(如"x∈[0,3],y∈[1,4]")] --> B[空间范围转H值区间<br>(四叉树递归分解非满象限)]
B --> C[合并相邻H值区间<br>(如9、11-15→8-15,减少查询次数)]
C --> D[遍历每个H值区间]
D --> E[B+树定位区间起始H值]
E --> F[遍历有序数据页<br>(按H值顺序获取区间内所有记录)]
F --> G[过滤空间上不满足原范围的记录<br>(排除"一维相邻但空间不相邻"数据)]
G --> H[合并结果并返回]
style A fill:#f9f,stroke:#333,stroke-width:1px
style H fill:#cfc,stroke:#333,stroke-width:1px关键节点:步骤 G 是空间范围查询的特有环节,因曲线存在 "空间邻近性丢失" 问题,需二次校验空间位置。
三、k 近邻查询(K-NN)流程图
核心逻辑:通过 "一维范围扩展 + 空间距离校验" 平衡效率与准确性,避免一次性查询过大范围。
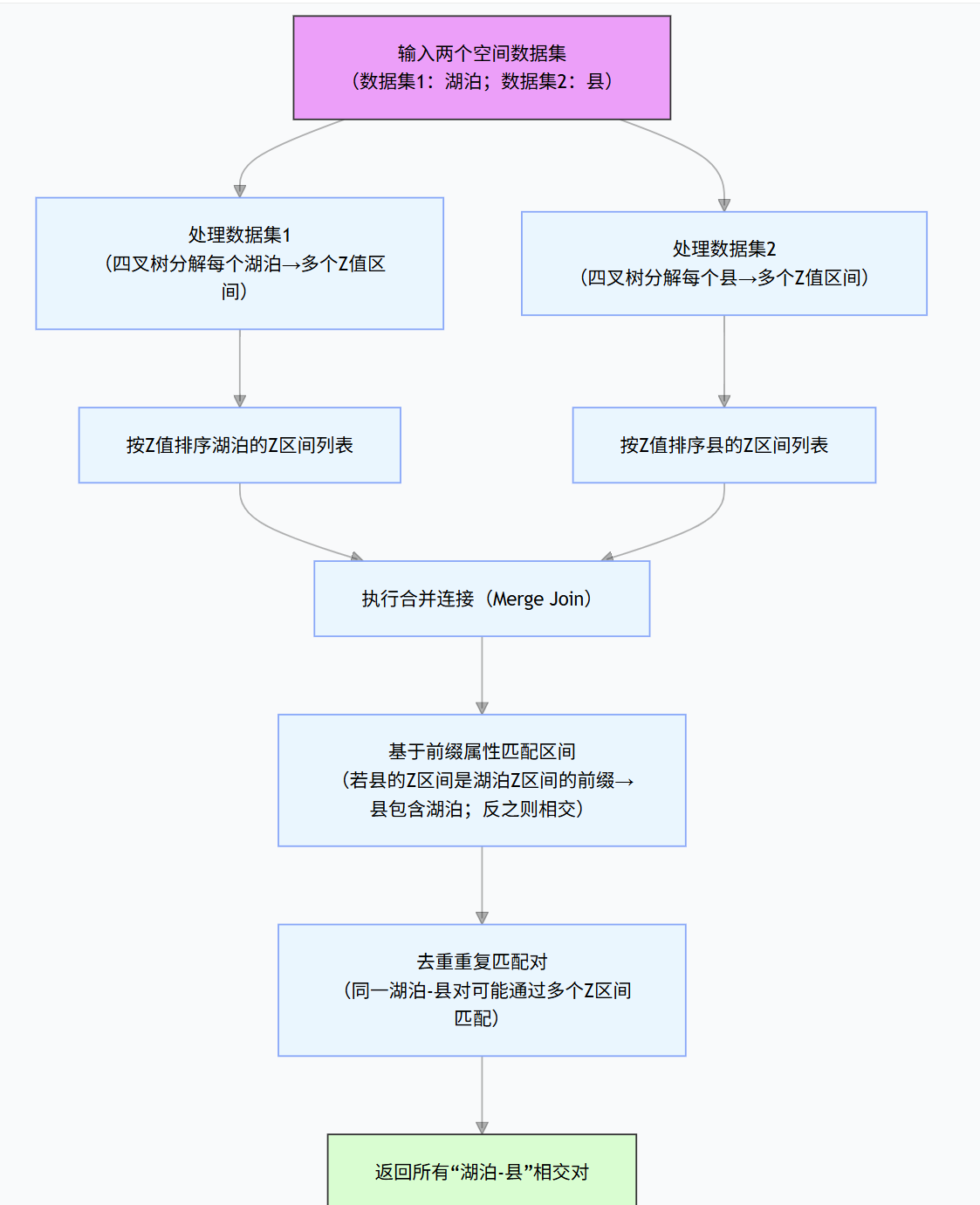
四、空间连接查询流程图(以 "湖泊 - 县" 相交查询为例)
你的 AI 助手,助力每日工作学习
关键规则:前缀属性是空间连接的核心判定依据(如 Z2=01**** 是 Z1=011001** 的前缀→Z2 区域包含 Z1 区域),避免逐一计算空间相交关系,降低复杂度。
流程图核心说明
- 共性逻辑:所有查询均遵循 "空间数据→一维 Z/H 值→索引查询→空间结果校验" 的路径,核心是通过一维映射复用 B + 树等成熟索引技术。
- 差异点:点查询无需范围扩展,范围查询需区间合并,k 近邻需动态扩范围,空间连接需前缀匹配,均针对场景优化效率。
- 依赖条件:需提前完成空间数据的 Z/H 值计算与有序存储(建议搭配 B + 树),否则查询效率会显著下降。