算法笔记 16 二分搜索算法

1 二分查找框架

cpp 复制代码

int binarySearch(vector<int>& nums, int target) {
    int left = 0, right = nums.size() - 1;

    while (...) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            ...
        } else if (nums[mid] < target) {
            left = ...
        } else if (nums[mid] > target) {
            right = ...
        }
    }
}

2 二分搜索框架

cpp 复制代码

class Solution {
public:
    // 标准的二分搜索框架，搜索目标元素的索引，若不存在则返回 -1
    int search(vector<int>& nums, int target) {
        int left = 0;
        // 注意
        int right = nums.size() - 1;

        while(left <= right) {
            int mid = left + (right - left) / 2;
            if(nums[mid] == target) {
                return mid;   
            } else if (nums[mid] < target) {
                // 注意
                left = mid + 1;
            } else if (nums[mid] > target) {
                // 注意
                right = mid - 1;
            }
        }
        return -1;
    }
};

要理解这个二分搜索算法的边界处理核心 ，关键在于抓住三个核心设计的一致性：**right 的初始化值、while 循环条件、left/right 的更新逻辑。**这三者必须配套，否则会出现死循环或漏查元素的问题。下面逐点拆解边界处理的细节：

一、核心前提：二分搜索的适用场景

该算法仅适用于 有序数组（无重复元素）------ 这是二分搜索的基础，只有数组有序，才能通过「中间元素与目标的大小比较」缩小搜索范围。

二、边界处理的三个关键细节（核心）

我们围绕「为什么这么设计」展开，对比错误设计的问题，突出正确逻辑的合理性。

1. 右边界初始化：`right = nums.size() - 1`（闭区间定义）

设计含义 ：搜索范围是 [left, right]（左闭右闭区间），即 left 和 right 指向的元素都属于待搜索范围 。
- 例：数组 [1,3,5,7]，初始 left=0，right=3，搜索范围是 [0,3]（包含所有元素）。
为什么不初始化为 right = nums.size()？
- 若 right = nums.size()，搜索范围变成 [left, right)（左闭右开），后续循环条件和更新逻辑必须跟着调整（比如 while(left < right)）。该算法选择「闭区间」是为了逻辑更直观（左右边界都包含有效元素）。
错误后果 ：若误写 right = nums.size()，且后续逻辑不变，当 target > nums.back() 时，right 会一直大于 left，导致循环无法终止（死循环）。

2. 循环条件：`while(left <= right)`（允许区间闭合）

设计含义 ：当 left == right 时，搜索范围是 [left, left]（单个元素），仍需检查该元素是否为目标 ------ 因为闭区间内的所有元素都要覆盖。
- 例：数组 [5]，target=5：left=0，right=0，循环执行 mid=0，判断 nums[0]==5，返回正确索引。
为什么不写 while(left < right)？
- 若用 left < right，当 left == right 时循环终止，会漏掉对最后一个元素的检查。
- 反例：数组 [5]，target=5：left=0，right=0，循环不执行，直接返回 -1（错误）。
边界临界情况 ：
- 数组为空（nums.size()=0）：right = -1，left=0 > right，循环不执行，返回 -1（正确，空数组无目标）。
- 目标小于所有元素（target < nums[0]）：最终 right 会小于 left，循环终止，返回 -1（正确）。
- 目标大于所有元素（target > nums.back()）：最终 left 会大于 right，循环终止，返回 -1（正确）。

3. 左右边界更新：`left = mid + 1` / `right = mid - 1`（排除已检查的 mid）

设计逻辑 ：因为 mid 位置的元素已经和 target 比较过（确定不是目标，或已返回），所以下一轮搜索范围必须排除 mid ，避免重复检查或死循环。
- 当 nums[mid] < target：目标在 mid 右侧，且 mid 已排除，所以 left = mid + 1（新范围 [mid+1, right]）。
- 当 nums[mid] > target：目标在 mid 左侧，且 mid 已排除，所以 right = mid - 1（新范围 [left, mid-1]）。
为什么不能写 left = mid 或 right = mid？
- 反例 1：数组 [1,3]，target=3：
  - 初始 left=0，right=1，mid=0，nums[0]=1 < 3，若 left=mid（仍为 0），则下一轮循环还是 left=0，right=1，mid=0------ 无限死循环。
- 反例 2：数组 [3,5]，target=3：
  - 初始 left=0，right=1，mid=0，nums[0]=3 == target，返回 0（正确）；若 target=2，nums[0]=3>2，若 right=mid（仍为 0），下一轮 left=0，right=0，mid=0，nums[0]>2，right=mid=-1，循环终止（正确）？------ 看似偶然正确，但在其他场景会出错：
    - 数组 [1,2,3]，target=4：mid=1（2<4）→ left=1 → 再次 mid=1 → 死循环。
核心原则 ：更新逻辑必须让搜索范围严格缩小（每轮至少减少 1 个元素），否则会陷入死循环。

三、边界处理的一致性验证（关键总结）

该算法的边界设计本质是「闭区间 [left, right] 的全程一致性」：

初始化：right = nums.size()-1 → 闭区间包含所有元素；
循环：left <= right → 闭区间不为空（仍有元素待查）；
更新：left=mid+1 / right=mid-1 → 闭区间排除已查元素，范围严格缩小。

三者缺一不可，一旦破坏一致性（比如 right 初始为 nums.size()，但循环条件还是 left<=right），就会出现错误。

四、常见错误案例分析（加深理解）

错误 1：`right = nums.size()` + `while(left <= right)`

数组 [1,3,5]，target=6：
- 初始 left=0，right=3，mid=1（3<6）→ left=2；
- mid=2（5<6）→ left=3；
- mid=3（nums[3] 越界！）→ 访问非法内存，程序崩溃。

错误 2：`while(left < right)` + `right = mid-1`

数组 [5]，target=5：
- 初始 left=0，right=0 → 循环不执行，返回 -1（漏查）。

错误 3：`left = mid` + `while(left <= right)`

数组 [1,3]，target=4：
- left=0，right=1 → mid=0（1<4）→ left=0（未更新）→ 死循环。

五、算法执行流程示例（直观感受边界变化）

以 nums = [1,3,5,7,9]，target=7 为例：

初始：left=0，right=4 → 范围 [0,4]；
mid=2（5<7）→ left=3 → 范围 [3,4]；
mid=3（7==7）→ 返回 3（正确）。

再以 target=4 为例：

初始：left=0，right=4 → mid=2（5>4）→ right=1 → 范围 [0,1]；
mid=0（1<4）→ left=1 → 范围 [1,1]；
mid=1（3<4）→ left=2 → 此时 left=2 > right=1，循环终止，返回 -1（正确）。

总结

该二分搜索的边界处理核心是「闭区间一致性」：

用 right = nums.size()-1 定义闭区间；
用 left <= right 保证闭区间内所有元素都被检查；
用 left=mid+1 / right=mid-1 排除已查元素，确保范围严格缩小。

这种设计的优势是逻辑直观、无冗余检查，且能覆盖所有边界情况（空数组、目标在数组外、目标在数组内），是二分搜索最经典、最不易出错的实现方式。

3 寻找左侧边界

cpp 复制代码

int left_bound(vector<int>& nums, int target) {
    int left = 0;
    // 注意
    int right = nums.size();
    
    // 注意
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            right = mid;
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            // 注意
            right = mid;
        }
    }
    return left;
}

这个算法是二分搜索的「左侧边界查找」变种。

（核心目标：找到第一个大于等于 target 的元素索引 ，或「target 第一次出现的位置」），其边界处理的核心是「左闭右开区间 [left, right) 」的全程一致性 ------ 和你之前问的「标准二分搜索」（闭区间 [left, right]）是两种不同的设计范式，但逻辑自洽。

一、先明确：左侧边界查找的核心目标

和标准二分（找「是否存在 target」）不同，左侧边界查找要解决的是：

若数组有重复元素（如 [1,2,2,3]），返回 target 第一次出现的索引（如 target=2 返 1）；
若数组无 target，返回 第一个大于 target 的元素索引（如 [1,3,5] 找 2，返 1；找 0 返 0；找 6 返 3）；
本质是找到「最小的 index，使得 nums [index] ≥ target」。

这个目标决定了算法不能找到 target 就直接返回，而是要「继续向左收缩范围」，直到锁定最左侧的边界。

二、边界处理的三个关键细节（左闭右开 [left, right) 范式）

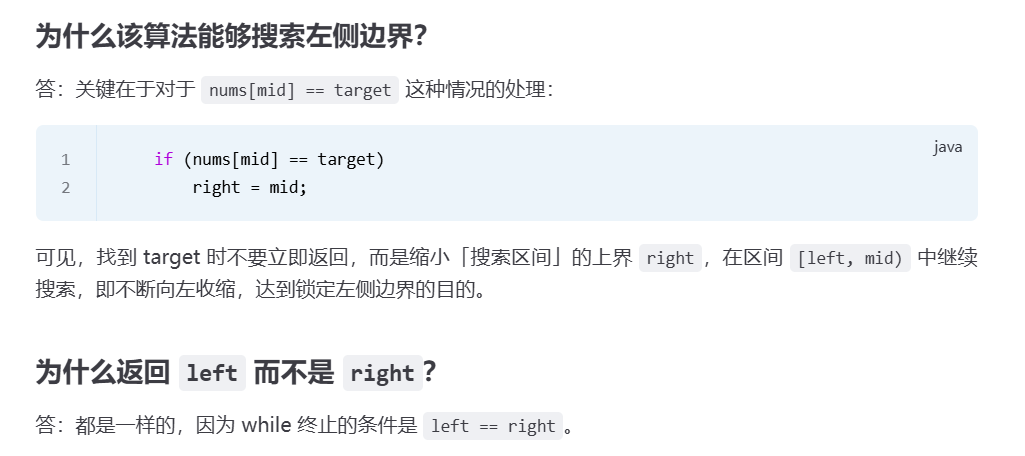
和标准二分的「闭区间」对比，左侧边界查找的所有设计都围绕「左闭右开」展开，三者必须严格一致：

1. 右边界初始化：`right = nums.size()`（而非 size-1）

设计含义 ：搜索范围是 [left, right)（左闭右开）------left 指向的元素属于待查范围，right 指向的元素不属于 待查范围（是范围的「哨兵」）。
- 例：数组 [1,2,2,3]，初始 left=0，right=4（数组长度 4），搜索范围是 [0,4)，即索引 0、1、2、3（刚好覆盖所有元素）。
为什么不初始化为 right = nums.size ()-1？
- 若用 right = size-1，就变成了闭区间 [left, right]，后续循环条件和更新逻辑要跟着改（会和「收缩找左边界」的目标冲突）。
- 关键：左闭右开区间的 right 本质是「待查范围的上限 + 1」，这样能自然处理「target 比所有元素大」的情况（最终返回 right = size，符合预期）。

2. 循环条件：`while (left < right)`（而非 left ≤ right）

设计含义 ：左闭右开区间 [left, right) 中，left == right 时，区间是空的（没有元素可查），循环终止。
- 例：待查范围 [2,2) → 无元素，直接退出。
为什么不能用 left ≤ right？
- 若用 left ≤ right，当 left == right 时，会进入循环，此时 mid = left = right，而 nums [right] 可能越界（因为 right 初始是 size，当 target 比所有元素大时，right 始终是 size，mid = size 会访问非法索引）。
- 核心：左闭右开区间的「有效范围」是 left < right，循环只需要处理有效范围。

3. 核心逻辑：找到 target 后，不返回，而是收缩右边界 `right = mid`

这是左侧边界查找和标准二分的本质区别 ------ 目标是找「最左侧」的 target，所以即使找到 mid 位置是 target，也不能停，要继续向左找，看看有没有更早出现的 target。

我们分三种情况拆解更新逻辑：

条件	说明	边界更新方式	新搜索范围	核心目的
nums[mid] == target	mid 可能是左边界，但也可能有更左的 target	right = mid	[left, mid)	收缩右边界，向左找更左的 target
nums[mid] < target	target 在 mid 右侧（mid 及左侧都太小）	left = mid + 1	[mid+1, right)	排除 mid 及左侧，向右找
nums[mid] > target	target 在 mid 左侧（mid 及右侧都太大）	right = mid	[left, mid)	排除 mid 及右侧，向左找

关键疑问 1：为什么 nums [mid] == target 时，要设 right = mid 而非 right = mid-1？
- 因为区间是左闭右开 [left, mid)，right = mid 意味着「下一轮只查 mid 左侧的元素」，但不会排除 mid 本身（因为新范围是 [left, mid)，mid 不属于新范围，但 mid 是当前找到的 target 位置，后续会通过 left 逼近 mid）。
- 例：nums = [1,2,2,3]，target=2，mid=2（nums [2]=2）→ right=2，新范围 [0,2) → 查索引 0、1，继续找左边界。
关键疑问 2：为什么 nums [mid] > target 时，也是 right = mid 而非 right = mid-1？
- 左闭右开区间 [left, right) 中，mid 属于当前范围（已检查），nums [mid] > target 说明 target 在左侧，所以新范围是 [left, mid)（排除 mid 及右侧），right 直接设为 mid 即可（因为 mid 不再属于新范围）。
- 对比标准二分：标准二分是闭区间，所以要 right = mid-1（排除 mid）；这里是左闭右开，right = mid 就等价于排除 mid。
关键疑问 3：为什么 nums [mid] < target 时，还是 left = mid + 1？
- 因为 nums [mid] < target，mid 及左侧都不可能是 target，所以直接排除 mid，left 设为 mid+1（新范围从 mid+1 开始），保证范围严格缩小。

三、执行流程示例（直观感受边界收缩）

示例 1：有重复元素，找 target 左边界

nums = [1,2,2,3,4]，target=2

初始：left=0，right=5（范围 [0,5)）
mid = 0 + (5-0)/2 = 2 → nums [2] = 2 == target → right=2（新范围 [0,2)）
mid = 0 + (2-0)/2 = 1 → nums [1] = 2 == target → right=1（新范围 [0,1)）
mid = 0 + (1-0)/2 = 0 → nums [0] = 1 < target → left=1（新范围 [1,1)）
left == right，循环终止 → 返回 left=1（正确，是 2 第一次出现的索引）

示例 2：无 target，找第一个大于 target 的元素

nums = [1,3,5,7]，target=4

初始：left=0，right=4（范围 [0,4)）
mid=2 → nums [2]=5 > 4 → right=2（新范围 [0,2)）
mid=1 → nums [1]=3 < 4 → left=2（新范围 [2,2)）
循环终止 → 返回 left=2（nums [2]=5，是第一个大于 4 的元素，正确）

示例 3：target 比所有元素小

nums = [2,4,6]，target=1

初始：left=0，right=3（范围 [0,3)）
mid=1 → nums [1]=4 > 1 → right=1（范围 [0,1)）
mid=0 → nums [0]=2 > 1 → right=0（范围 [0,0)）
循环终止 → 返回 left=0（正确，第一个大于 1 的元素是 nums [0]=2）

示例 4：target 比所有元素大

nums = [2,4,6]，target=7

初始：left=0，right=3（范围 [0,3)）
mid=1 → nums [1]=4 <7 → left=2（范围 [2,3)）
mid=2 → nums [2]=6 <7 → left=3（范围 [3,3)）
循环终止 → 返回 left=3（等于数组长度，说明 target 不存在，且所有元素都比 target 小）

四、返回值的特殊处理（重要）

算法最终返回 left（或 right，因为循环终止时 left == right），但需要根据实际需求判断是否存在 target：

若要判断「target 是否存在」：返回后需检查 left 是否在数组范围内，且 nums[left] == target。
- 例：nums = [1,3,5]，target=2 → 返回 left=1，但 nums [1]=3≠2 → 说明 target 不存在。
若只需要「第一个大于等于 target 的索引」（如插入位置）：直接返回 left 即可（无需判断）。

补充完整的「带存在性检查」的左侧边界查找：

cpp 复制代码

int left_bound(vector<int>& nums, int target) {
    int left = 0;
    int right = nums.size();
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            right = mid;
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else {
            right = mid;
        }
    }
    // 存在性检查：left 越界（target 比所有元素大）或 nums[left] != target → 不存在
    if (left >= nums.size() || nums[left] != target) {
        return -1; // 表示 target 不存在
    }
    return left; // 存在，返回左边界索引
}

五、和标准二分的核心区别（对比记忆）

设计维度	标准二分（找目标索引）	左侧边界查找（找左边界）
核心目标	判断 target 是否存在，返回任意索引	找 target 第一次出现的索引（或插入位置）
区间定义	闭区间 [left, right]	左闭右开区间 [left, right)
right 初始化	nums.size()-1	nums.size()
循环条件	left ≤ right	left < right
找到 target 后	直接返回 mid	不返回，right = mid（收缩左边界）
nums [mid] > target 时	right = mid-1	right = mid
循环终止后	未找到返回 -1	返回 left（需额外检查是否存在 target）

总结

左侧边界查找的核心是「左闭右开区间 + 找到 target 后收缩右边界」：

区间定义 [left, right) 是所有边界设计的基础，确保 right 初始化、循环条件、更新逻辑一致；
关键动作是 nums[mid] == target 时不返回，而是 right = mid，持续向左收缩，锁定最左侧的 target；
返回值 left 本质是「第一个大于等于 target 的索引」，需根据需求判断是否存在 target。

这种设计能高效处理**「重复元素找左边界」「找插入位置」** 等场景，时间复杂度仍是 O (log n)，和标准二分一致。

4搜索区间：二分搜索的「范围核心」

搜索区间，本质是二分搜索中「当前仍需检查的元素范围」------ 它是用左右指针（left、right）定义的一个连续索引区间 ，所有可能满足目标条件（比如等于 target、是 target 左边界）的元素，都必须在这个区间内。

二分搜索的核心逻辑，就是不断缩小搜索区间 （每次排除一半不可能的元素），直到区间为空（没找到）或找到目标（直接返回）。而你之前接触的「标准二分」和「左侧边界二分」，本质区别就是「搜索区间的定义不同」------ 区间定义直接决定了 right 初始化、循环条件、指针更新这三大关键细节（必须三者一致，否则出错）。

一、搜索区间的两种核心定义（二分的两大范式）

二分搜索的搜索区间只有两种主流定义，所有边界处理都围绕这两种定义展开，我们用表格对比，结合你熟悉的代码理解：

定义类型	核心形式	适用场景	关键特征（左右指针含义）
左闭右闭区间	`[left, right]`	标准二分（找目标是否存在）	`left` 和 `right` 指向的元素「都属于待检查范围」
左闭右开区间	`[left, right)`	左侧 / 右侧边界查找	`left` 指向的元素属于待查范围，`right` 是「范围哨兵」（不属于待查范围）

1. 左闭右闭区间 `[left, right]`（标准二分的搜索区间）

对应你第一次问的「标准二分搜索」，搜索区间的规则很直观：

区间内的所有索引 i（满足 left ≤ i ≤ right），都是**「还没检查过、可能是目标」**的元素；
比如数组 [1,3,5,7]，初始搜索区间是 [0,3]（left=0，right=3），意味着要检查索引 0、1、2、3 对应的所有元素；
缩小区间时，必须排除已经检查过的 mid（因为 mid 已经和 target 对比过）：
- 若 nums[mid] < target：mid 及左侧都不可能是目标，区间缩小为 [mid+1, right]（left=mid+1）；
- 若 nums[mid] > target：mid 及右侧都不可能是目标，区间缩小为 [left, mid-1]（right=mid-1）；
区间为空的条件：left > right（比如 left=4，right=3），此时没有元素可查，循环终止。

2. 左闭右开区间 `[left, right)`（左侧边界的搜索区间）

对应你第二次问的「左侧边界查找」，搜索区间的规则是**「左包含、右不包含」**：

区间内的所有索引 i（满足 left ≤ i < right），才是待检查元素；right 指向的索引「永远不检查」，只是用来标记范围的上限；
比如数组 [1,2,2,3]，初始搜索区间是 [0,4]（left=0，right=4），实际检查的是索引 0、1、2、3（刚好覆盖所有元素）；
缩小区间时，同样排除已检查的 mid，但因为「右不包含」，更新逻辑有差异：
- 若 nums[mid] < target：mid 及左侧无效，区间缩小为 [mid+1, right]（left=mid+1）；
- 若 nums[mid] > target：mid 及右侧无效，区间缩小为 [left, mid]（right=mid，因为 mid 不再属于新区间，无需减 1）；
- 若 nums[mid] == target：不返回，继续向左找左边界，区间缩小为 [left, mid]（right=mid，排除 mid 右侧，保留左侧可能的更早的 target）；
区间为空的条件：left == right（比如 left=2，right=2），此时没有元素可查，循环终止。

二、为什么搜索区间是「二分的核心」？

所有二分的边界错误（死循环、漏查、越界），本质都是「搜索区间定义与代码逻辑不一致」。比如：

若你把左侧边界查找的 right 初始化为 nums.size()-1（按闭区间初始化），但循环条件还是 left < right（左闭右开的循环条件），就会漏查最后一个元素；
若你用闭区间 [left, right]，但 nums[mid] > target 时更新 right=mid（而非 mid-1），就会陷入死循环（比如 nums=[1,3]，target=2，left=0、right=1 会一直重复）。

简单说：先确定搜索区间的定义，再推导对应的 right 初始化、循环条件、指针更新逻辑，这是二分搜索不出错的关键。

三、搜索区间的直观理解（用例子感受）

以「左侧边界查找」nums=[1,2,2,3]，target=2 为例：

初始搜索区间：[0,4) → 待查索引 0、1、2、3；
第一次 mid=2（nums[2]=2）：区间缩小为 [0,2) → 待查索引 0、1（排除 mid=2 及右侧，向左找更左的 2）；
第二次 mid=1（nums[1]=2）：区间缩小为 [0,1) → 待查索引 0（继续排除 mid=1 及右侧）；
第三次 mid=0（nums[0]=1 < 2）：区间缩小为 [1,1) → 区间为空，循环终止；
最终返回 left=1（正确的左边界）。

整个过程中，搜索区间始终是「左闭右开」，每一步缩小都严格遵循「排除无效元素、保留可能目标」的原则，没有冗余检查，也不会越界。

总结

搜索区间是二分搜索的「规则前提」------ 它定义了「哪些元素还需要检查」，进而决定了代码的所有关键细节：

先明确是「左闭右闭 [left, right]」还是「左闭右开 [left, right)」；
按区间定义初始化 right（闭区间用 size-1，开区间用 size）；
按区间「为空的条件」写循环（闭区间 left ≤ right，开区间 left < right）；
按「排除已检查的 mid」更新指针（闭区间需 mid±1，开区间右侧直接设 mid）。

记住：搜索区间的一致性，是二分搜索正确的核心保障。

5 二分搜索总体思路模板：从「明确目标」到「代码落地」

二分搜索的核心痛点是「边界混乱」，但只要遵循「先定目标→选区间范式→推三大细节→验证边界」的固定流程，就能解决 99% 的二分问题。

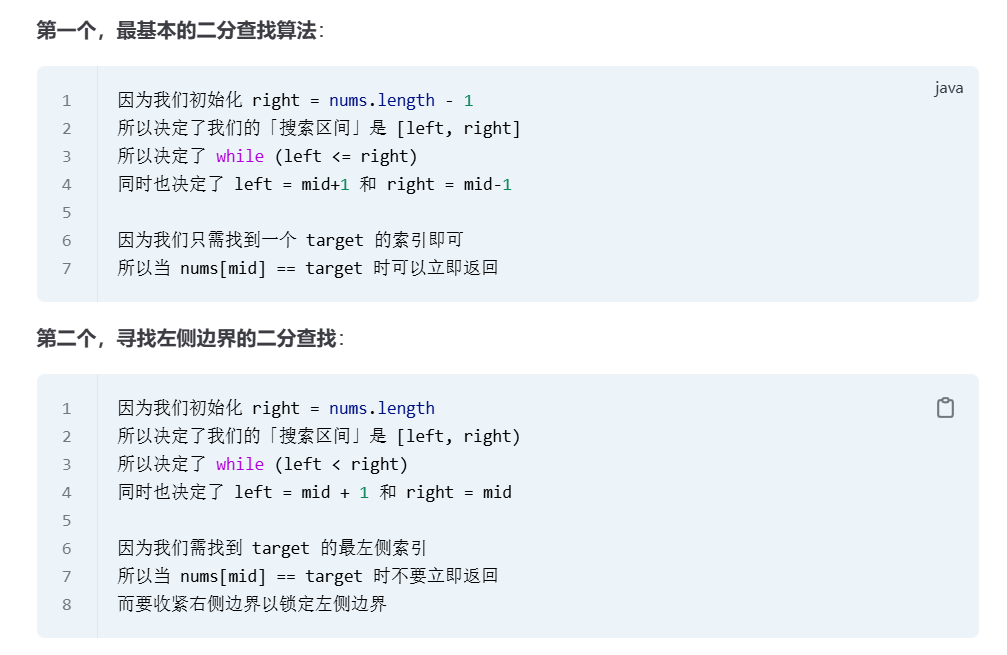
一、二分搜索适用场景（先判断能不能用）

首先明确：不是所有问题都能二分，必须满足 2 个前提：

有序性：数组 / 区间是「单调的」（升序 / 降序，大部分题目是升序）；
可二分性：能通过「中间元素与目标的比较」，直接排除一半无效范围。

常见适用问题：

基础：找目标元素是否存在（标准二分）；
边界：找目标的左边界（第一次出现）、右边界（最后一次出现）；
扩展：找插入位置、找满足条件的最大值 / 最小值（如「最小的大于 target 的元素」）。

二、万能分析思路模板（4 步走，必不慌）

Step 1：明确「核心目标」（最关键，决定后续逻辑）

先问自己：我要找的是什么？用「一句话 + 数学表达式」定义清楚，避免模糊。

问题类型	核心目标（一句话）	数学表达式（升序数组）
标准查找	找到任意一个等于 target 的元素索引，无则返回 -1	nums[index] == target
左边界查找	找到第一个 ≥ target 的元素索引（或 target 第一次出现位置）	index 是最小的，满足 nums [index] ≥ target
右边界查找	找到最后一个 ≤ target 的元素索引（或 target 最后一次出现位置）	index 是最大的，满足 nums [index] ≤ target
插入位置查找	找到 target 应该插入的索引（不破坏有序性）	等价于「左边界查找」（插入到第一个 ≥ target 的位置）

👉 示例：题目「在排序数组中查找元素的第一个和最后一个位置」

34. 在排序数组中查找元素的第一个和最后一个位置

→ 核心目标是「左边界 + 右边界」。

Step 2：选择「区间范式」（二选一，全程不变）

二分的边界问题，本质是「搜索区间的定义」。推荐优先选择 左闭右开 [left, right) 范式 ------ 因为左右边界查找逻辑对称，不易出错，且能自然处理「越界」情况。

两种范式对比（选好后全程不换）：

范式	左闭右开 `[left, right)`（推荐）	左闭右闭 `[left, right]`（备选）
区间含义	left 属于待查范围，right 是哨兵（不属于）	left 和 right 都属于待查范围
初始值	left=0，right=nums.size()	left=0，right=nums.size()-1
循环条件	while (left < right)（区间非空）	while (left ≤ right)（区间非空）
排除 mid 的方式	右边界更新：right=mid（无需减 1）	右边界更新：right=mid-1
循环终止后	left == right（返回 left 或 left-1）	left > right（返回 -1 或中间结果）

👉 约定：后续所有案例都用「左闭右开 [left, right)」范式（记住：选好就不换！）。

Step 3：推导「三大核心细节」（基于目标和范式）

根据「核心目标」和「区间范式」，推导以下 3 个细节（直接套用逻辑，不用死记）：

细节 1：mid 的计算（固定写法，避免溢出）

无论什么问题，mid 都用「向下取整」的安全写法（避免 int 溢出）：

cpp 复制代码

int mid = left + (right - left) / 2;  // 等价于 (left+right)/2，但无溢出风险

👉 注意：只有「左开右闭 (left, right]」范式的右边界查找需要向上取整（我们不用这个范式，所以不用记）。

细节 2：指针更新逻辑（核心！按目标分情况）

根据「mid 位置元素与 target 的关系」，决定如何缩小范围 ------ 核心原则是「排除无效元素，保留可能满足目标的范围」。

按「核心目标」分类，直接套用以下逻辑（升序数组）：

问题类型	nums [mid] < target 时	nums [mid] == target 时	nums [mid] > target 时
标准查找	left = mid + 1（目标在右）	return mid（找到直接返回）	right = mid（目标在左）
左边界查找	left = mid + 1（mid 及左都太小）	right = mid（不返回，向左找更左的）	right = mid（mid 及右都太大）
右边界查找	left = mid + 1（mid 及左都太小，向右找）	left = mid + 1（不返回，向右找更右的）	right = mid（mid 及右都太大）

👉关键记忆点：

左边界查找：找到 target 后「收缩右边界」（right=mid），向左逼近；
右边界查找：找到 target 后「扩大左边界」（left=mid+1），向右逼近；
标准查找：找到 target 直接返回（不用找边界）。

细节 3：循环终止后的返回值处理（避免漏查 / 误判）

循环终止时，left == right（左闭右开范式），但返回值需根据「核心目标」调整，且必须加「存在性检查」（避免 target 不存在时返回错误索引）。

各问题类型的返回值逻辑：

问题类型	初步返回值	存在性检查（避免错误）	最终返回值
标准查找	-1（循环内没返回就是不存在）	无需额外检查（循环内找到已返回）	循环内返回 mid，否则 -1
左边界查找	left	1. left 越界（left >= nums.size ()）→ 不存在；2. nums [left] != target → 不存在	存在则返回 left，否则 -1
右边界查找	left - 1（因为最后一次找到 target 时 left=mid+1）	1. ans < 0（left=0 → ans=-1）→ 不存在；2. nums [ans] != target → 不存在	存在则返回 ans，否则 -1
插入位置查找	left	无需检查（即使 target 不存在，left 也是正确插入位置）	直接返回 left

👉 示例：左边界查找中，nums=[1,3,5]，target=2 → left=1，但 nums [1]=3≠2 → 存在性检查失败，返回 -1（表示 target 不存在）。

Step 4：验证「边界测试用例」（确保无错）

写好代码后，必须用 3 类边界用例测试（覆盖所有极端情况）：

target 比所有元素小（如 nums=[2,4,6]，target=1）；
target 比所有元素大（如 nums=[2,4,6]，target=7）；
数组为空（nums=[]）或只有一个元素（nums=[5]）；
数组有重复元素（如 nums=[1,2,2,3]，target=2）。

👉 测试原则：只要有一个用例出错，就回到 Step 3 检查「指针更新逻辑」或「返回值处理」。

三、实战案例：用模板解决 3 类经典问题

案例 1：标准查找（LeetCode 704. 二分查找）

问题：

给定升序无重复数组，查找 target，存在返回索引，否则返回 -1。

按模板分析：

核心目标：nums [index] == target；
区间范式：左闭右开 [left, right)；
三大细节：
- mid：left + (right - left)/2；
- 指针更新：
  - nums[mid] < target → left=mid+1；
  - nums[mid] == target → return mid；
  - nums[mid] > target → right=mid；
- 返回值：循环内没返回则返回 -1（无需额外检查）。

代码：

cpp 复制代码

int search(vector<int>& nums, int target) {
    int left = 0;
    int right = nums.size();  // 左闭右开
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            return mid;  // 找到直接返回
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else {
            right = mid;
        }
    }
    return -1;  // 循环结束没找到
}

测试用例：

nums=[-1,0,3,5,9,12]，target=9 → 返回 4（正确）；
nums=[-1,0,3,5,9,12]，target=2 → 返回 -1（正确）；
nums=[5]，target=5 → 返回 0（正确）；
nums=[5]，target=3 → 返回 -1（正确）。

案例 2：左边界查找（LeetCode 34. 查找元素的第一个和最后一个位置 - 左边界部分）

问题：

给定升序数组（可能有重复），找到 target 第一次出现的索引，无则返回 -1。

按模板分析：

核心目标：最小的 index，满足 nums [index] ≥ target；
区间范式：左闭右开 [left, right)；
三大细节：
- mid：left + (right - left)/2；
- 指针更新：
  - nums[mid] < target → left=mid+1；
  - nums [mid] == target → right=mid（收缩右边界，向左找）；
  - nums[mid] > target → right=mid；
- 返回值：
  - 初步返回 left；
  - 存在性检查：left >= nums.size () 或 nums [left] != target → 返回 -1；
  - 否则返回 left。

代码：

cpp 复制代码

int left_bound(vector<int>& nums, int target) {
    int left = 0;
    int right = nums.size();
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            right = mid;  // 不返回，继续向左找
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else {
            right = mid;
        }
    }
    // 存在性检查
    if (left >= nums.size() || nums[left] != target) {
        return -1;
    }
    return left;
}

测试用例：

nums=[1,2,2,3]，target=2 → 返回 1（正确）；
nums=[1,3,5]，target=2 → left=1，nums [1]=3≠2 → 返回 -1（正确）；
nums=[2,4,6]，target=1 → left=0，nums [0]=2≠1 → 返回 -1（正确）；
nums=[2,4,6]，target=7 → left=3 ≥ 3 → 返回 -1（正确）。

案例 3：右边界查找（LeetCode 34. 查找元素的第一个和最后一个位置 - 右边界部分）

问题：

给定升序数组（可能有重复），找到 target 最后一次出现的索引，无则返回 -1。

按模板分析：

核心目标：最大的 index，满足 nums [index] ≤ target；
区间范式：左闭右开 [left, right)；
三大细节：
- mid：left + (right - left)/2；
- 指针更新：
  - nums[mid] < target → left=mid+1；
  - nums [mid] == target → left=mid+1（扩大左边界，向右找）；
  - nums[mid] > target → right=mid；
- 返回值：
  - 初步返回 left-1（因为最后一次找到 target 时 left=mid+1，多走了一步）；
  - 存在性检查：ans <0 或 nums [ans] != target → 返回 -1；
  - 否则返回 ans。

代码：

cpp 复制代码

int right_bound(vector<int>& nums, int target) {
    int left = 0;
    int right = nums.size();
    while (left < right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            left = mid + 1;  // 不返回，继续向右找
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else {
            right = mid;
        }
    }
    int ans = left - 1;  // 修正多走的一步
    // 存在性检查
    if (ans < 0 || nums[ans] != target) {
        return -1;
    }
    return ans;
}

测试用例：

nums=[1,2,2,3]，target=2 → ans=3-1=2 → 返回 2（正确）；
nums=[1,3,5]，target=2 → ans=1-1=0，nums [0]=1≠2 → 返回 -1（正确）；
nums=[2,4,6]，target=1 → ans=0-1=-1 → 返回 -1（正确）；
nums=[2,4,6]，target=7 → ans=3-1=2，nums [2]=6≠7 → 返回 -1（正确）。

四、常见错误避坑指南（必看！）

循环条件写错 ：左闭右开范式用了 left <= right → 导致越界（如 right=nums.size () 时，mid 可能等于 nums.size ()）；
指针更新漏 +1 ：左闭右开范式中，nums [mid] < target 时写 left=mid → 死循环（如 nums=[1,3]，target=3，left 永远停在 0）；
右边界查找忘记减 1：直接返回 left 而非 left-1 → 结果比正确值大 1；
存在性检查缺失：左边界查找直接返回 left，没检查 nums [left] 是否等于 target → target 不存在时返回错误索引；
mid 计算溢出 ：用 (left+right)/2 而非 left + (right-left)/2 → 当 left 和 right 接近 INT_MAX 时溢出。

五、总结：模板核心口诀

先定目标：一句话说清要找啥，用数学表达式量化；
再选范式：优先左闭右开 [left, right)，初始 right 设 size；
推导细节：mid 安全写，更新看目标（左边界收缩右，右边界扩大左）；
验证边界：极端用例测三遍，存在性检查不能少。

按照这个模板，每次写二分前都按步骤走一遍，不用死记代码，而是理解逻辑，慢慢就会形成肌肉记忆，再也不会怕二分搜索了！

6 （补充）通俗理解 int 溢出：变量 "装不下" 数值了！

int 溢出，本质是：int 类型的变量有固定的数值存储范围，当你要存储的数值超过这个范围时，它会 "溢出"------ 就像水杯装满水后，多余的水会洒出来，变量里的数值也会变得错乱、不符合预期。

一、先搞懂：int 能装多大的数？（关键前提）

在 C++ 中，int 是「有符号整数类型」，它的存储范围由计算机的位数决定（绝大多数现代环境是 32 位 int）：

32 位 int 的范围：-2^31 到 2^31 - 1（即 -2147483648 到 2147483647）；
可以理解为：int 变量就像一个 "容量固定的盒子"，最多能装 2147483647 这个正数，最小能装 -2147483648 这个负数。

如果你的计算结果超出这个范围（比如 2147483647 + 1，或 -2147483648 - 1），就会发生「溢出」。

二、溢出后会发生什么？（直观例子）

32 位 int 的溢出遵循「模运算规则」，但不用记复杂公式，看例子就懂：

1. 正数溢出（超过 2147483647）

比如计算 2147483647 + 1：

预期结果：2147483648；
实际结果：-2147483648（直接跳到 int 能存储的最小负数）；
再比如 2147483647 + 2 → 实际结果：-2147483647。

就像钟表：时针转到 12 点后，再转 1 格就回到 1 点 ------int 的正数范围 "转到头"，就会跳到负数范围。

2. 负数溢出（小于 -2147483648）

比如计算 -2147483648 - 1：

预期结果：-2147483649；
实际结果：2147483647（直接跳到 int 能存储的最大正数）；

同样像钟表：时针转到 1 点后，再往回转 1 格就到 12 点 ------ 负数范围 "转到头"，就会跳到正数范围。

3. 二分搜索中最容易出现的溢出场景

就是你之前接触的「mid 计算」：

cpp 复制代码

// 错误写法：可能溢出
int mid = (left + right) / 2;

比如：当 left = 2147483647，right = 2147483647（极端情况，比如找比所有元素大的目标）：

left + right = 2147483647 + 2147483647 = 4294967294；
这个结果远超 int 的最大范围 2147483647，发生溢出；
溢出后 left + right 会变成 -2（按 32 位 int 规则）；
最终 mid = -2 / 2 = -1，而数组索引没有负数，访问 nums[mid] 会直接程序崩溃！

三、为什么 `left + (right - left) / 2` 能避免溢出？

我们拆解这个公式，就能发现它和 (left + right) / 2 是「数学等价」的，但计算过程不会溢出：

1. 数学推导（简单版）

复制代码

left + (right - left) / 2 = (2left + right - left) / 2 = (left + right) / 2

两个公式的结果完全一样，但计算顺序不同：

错误写法 (left + right)/2：先算加法（可能溢出），再算除法；
正确写法 left + (right-left)/2：先算减法（right - left，结果一定小于 right，不会溢出），再算除法，最后加 left（也不会溢出）。

2. 用溢出场景验证

还是 left = 2147483647，right = 2147483647：

先算 right - left = 2147483647 - 2147483647 = 0；
再算 0 / 2 = 0；
最后算 left + 0 = 2147483647；
最终 mid = 2147483647（虽然数组索引可能越界，但这是后续逻辑要处理的，至少不会因为 mid 计算崩溃）。

四、总结

int 溢出：int 变量的数值超过其存储范围（-2147483648 ~ 2147483647），导致数值错乱；
二分搜索中，(left + right)/2 会因 left 和 right 过大而溢出，导致程序崩溃；
解决方案：用 left + (right - left)/2 替代，本质是「改变计算顺序，避免先算大数加法」，既保证结果正确，又不会溢出；
延伸：如果需要处理更大的数（比如超过 2147483647），可以用 long long 类型（范围更大），但二分搜索中用 left + (right - left)/2 已经足够安全，是行业标准写法。

算法笔记 16 二分搜索算法

1 二分查找框架

2 二分搜索框架

一、核心前提：二分搜索的适用场景

二、边界处理的三个关键细节（核心）

1. 右边界初始化：right = nums.size() - 1（闭区间定义）

2. 循环条件：while(left <= right)（允许区间闭合）

3. 左右边界更新：left = mid + 1 / right = mid - 1（排除已检查的 mid）

三、边界处理的一致性验证（关键总结）

四、常见错误案例分析（加深理解）

错误 1：right = nums.size() + while(left <= right)

错误 2：while(left < right) + right = mid-1

错误 3：left = mid + while(left <= right)

五、算法执行流程示例（直观感受边界变化）

总结

3 寻找左侧边界

一、先明确：左侧边界查找的核心目标

二、边界处理的三个关键细节（左闭右开 [left, right) 范式）

1. 右边界初始化：right = nums.size()（而非 size-1）

2. 循环条件：while (left < right)（而非 left ≤ right）

3. 核心逻辑：找到 target 后，不返回，而是收缩右边界 right = mid

三、执行流程示例（直观感受边界收缩）

示例 1：有重复元素，找 target 左边界

示例 2：无 target，找第一个大于 target 的元素

示例 3：target 比所有元素小

示例 4：target 比所有元素大

四、返回值的特殊处理（重要）

五、和标准二分的核心区别（对比记忆）

总结

4搜索区间：二分搜索的「范围核心」

一、搜索区间的两种核心定义（二分的两大范式）

1. 左闭右闭区间 [left, right]（标准二分的搜索区间）

2. 左闭右开区间 [left, right)（左侧边界的搜索区间）

二、为什么搜索区间是「二分的核心」？

三、搜索区间的直观理解（用例子感受）

总结

5 二分搜索总体思路模板：从「明确目标」到「代码落地」

一、二分搜索适用场景（先判断能不能用）

二、万能分析思路模板（4 步走，必不慌）

Step 1：明确「核心目标」（最关键，决定后续逻辑）

Step 2：选择「区间范式」（二选一，全程不变）

Step 3：推导「三大核心细节」（基于目标和范式）

细节 1：mid 的计算（固定写法，避免溢出）

细节 2：指针更新逻辑（核心！按目标分情况）

细节 3：循环终止后的返回值处理（避免漏查 / 误判）

Step 4：验证「边界测试用例」（确保无错）

三、实战案例：用模板解决 3 类经典问题

案例 1：标准查找（LeetCode 704. 二分查找）

问题：

按模板分析：

代码：

测试用例：

案例 2：左边界查找（LeetCode 34. 查找元素的第一个和最后一个位置 - 左边界部分）

问题：

按模板分析：

代码：

测试用例：

案例 3：右边界查找（LeetCode 34. 查找元素的第一个和最后一个位置 - 右边界部分）

问题：

按模板分析：

代码：

测试用例：

四、常见错误避坑指南（必看！）

五、总结：模板核心口诀

6 （补充）通俗理解 int 溢出：变量 "装不下" 数值了！

一、先搞懂：int 能装多大的数？（关键前提）

二、溢出后会发生什么？（直观例子）

1. 正数溢出（超过 2147483647）

2. 负数溢出（小于 -2147483648）

3. 二分搜索中最容易出现的溢出场景

三、为什么 left + (right - left) / 2 能避免溢出？

1. 数学推导（简单版）

2. 用溢出场景验证

四、总结

1. 右边界初始化：`right = nums.size() - 1`（闭区间定义）

2. 循环条件：`while(left <= right)`（允许区间闭合）

3. 左右边界更新：`left = mid + 1` / `right = mid - 1`（排除已检查的 mid）

错误 1：`right = nums.size()` + `while(left <= right)`

错误 2：`while(left < right)` + `right = mid-1`

错误 3：`left = mid` + `while(left <= right)`

1. 右边界初始化：`right = nums.size()`（而非 size-1）

2. 循环条件：`while (left < right)`（而非 left ≤ right）

3. 核心逻辑：找到 target 后，不返回，而是收缩右边界 `right = mid`

1. 左闭右闭区间 `[left, right]`（标准二分的搜索区间）

2. 左闭右开区间 `[left, right)`（左侧边界的搜索区间）

三、为什么 `left + (right - left) / 2` 能避免溢出？