在分析简单电路时,一般应用欧姆定律和电阻的串、并联规律,但用它们来分析复杂电路就比较困难。这里的简单电路通常是指只有一个电源的电路,而复杂电路通常是指有两个或两个以上电源的电路。对于复杂电路,常用基尔霍夫定律、叠加定理和戴维南定理进行分析。
基尔霍夫定律
基尔霍夫定律又可分为基尔霍夫第一定律(又称基尔霍夫电流定律)和基尔霍夫第二定律(又称基尔霍夫电压定律)
基尔霍夫第一定律(电流定律)
基尔霍夫第一定律指出,在电路中,流入任意一个节点的电流之和等于流出该节点的电流之和,即
∑I入=∑I出\sum I_入 = \sum I_出∑I入=∑I出如果规定流入节点的电流为正,流出节点的电流为负,那么基尔霍夫第一定律也可以这样叙述:在电路中任意一个节点上,电流的代数和等于0A,即
∑I=0A\sum I = 0{\rm{A}}∑I=0A基尔霍夫第一定律不但适合于电路中的节点,对一个封闭面也是适用的。如下图所示,图(a)所示示意图中流入三极管的电流与流出的电流相等;图(b)所示电路中,流入三角形负载的电流与流出的电流相等。
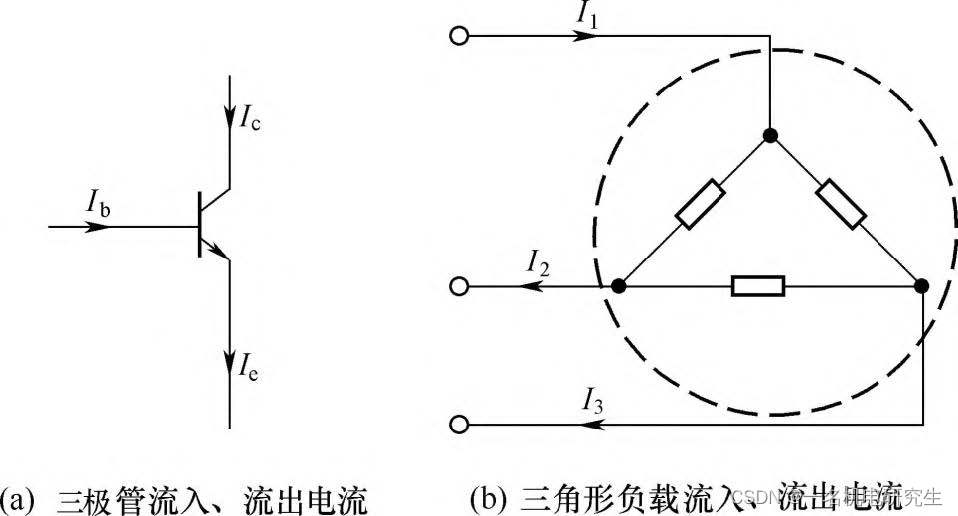
基尔霍夫第二定律(电压定律)
基尔霍夫第二定律指出,电路中任一回路内各段电压的代数和等于0V,即
∑U=0V\sum U = 0{\rm{V}}∑U=0V在应用基尔霍夫第二定律分析电路时,需要先规定回路的绕行方向。当流过回路中某元件的电流方向与绕行方向一致时,该元件两端的电压取正,反之取负;电源的电动势方向(电源的电动势方向始终是由负极指向正极)与绕行方向一致时,电源的电动势取负,反之取正。
叠加定理
对于一个元件,如果它两端的电压与流过的电流成正比,这种元件就被称为线性元件。线性电路是由线性元件组成的电路。电阻就是一种最常见的线性元件。叠加定理是反映线性电路基本性质的一个重要定理。
叠加定理的内容是:在线性电路中,任一支路中的电流(或电压)等于各个电源单独作用在此支路中所产生的电流(或电压)的代数和。
戴维南定理
对于一个复杂电路,如果需要求多条支路的电流大小,可以应用基尔霍夫定律或叠加定理。如果仅需要求一条支路中的电流大小,则应用戴维南定理更为方便。
在介绍戴维南定理之前,先来说明一下二端网络。任何具有两个出线端的电路都可以称为二端网络。包含有电源的二端网络称为有源二端网络,否则就称为无源二端网络。
戴维南定理的内容是:任何一个有源二端网络都可以用一个等效电源电动势E0E_0E0和内阻R0R_0R0串联起来的电路来代替。等效电源电动势E0E_0E0是该有源二端网络开路时的端电压;内阻R0R_0R0是指从两个端点向有源二端网络内看进去,并将电源均当成短路时的等效电阻。
最大功率传输定理与阻抗变换
最大功率传输定理
在电路中,往往希望负载能从电源中获得最大的功率,怎样才能做到这一点呢?如下图所示, EEE为电源,RRR为电源的内阻,RLR_LRL为负载电阻,III为流过负载RLR_LRL的电流,UUU为负载两端的电压。负载RLR_LRL获得的功率P=UIP=UIP=UI,当增大RLR_LRL的阻值时,电压UUU会增大,但电流III会减小;如果减小RLR_LRL的阻值,虽然电流III会增大,但电压UUU会减小。什么情况下功率PPP的值最大呢?
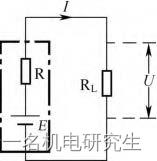
最大功率传输定理的内容是:负载要从电源获得最大功率的条件是负载的电阻(阻抗)与电源的内阻相等。
负载的电阻与电源的内阻相等又称两者阻抗匹配。
在上图中,负载RLR_LRL要从电源获得最大功率的条件是RL=RR_L=RRL=R,此时RLR_LRL得到的最大功率是
P=E24RLP=\dfrac{E^2}{4R_L}P=4RLE2如果有多个电源向一个负载供电,这时就要先用戴维南定理求出该电路的等效内阻R0R_0R0和等效电动势E0E_0E0,只要RL=R0R_L=R_0RL=R0,负载就可以获得最大功率。
阻抗变换
当负载的阻抗与电源的内阻相等时,负载才能从电源中获得最大功率,但很多电路的负载阻抗与电源的内阻并不相等,这种情况下怎么才仍能让负载获得最大功率呢?解决方法是进行阻抗变换,阻抗变换通常采用变压器。下面以图所示电路为例来说明变压器的阻抗变换原理。
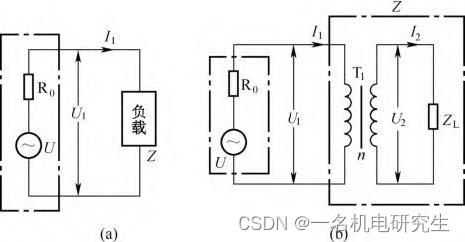
在图(a)所示电路中,要使负载从电源中获得最大功率,需让负载的阻抗ZZZ与电源(这里为信号源)内阻 R0R_0R0大小相等,即Z=R0Z=R_0Z=R0。这里的负载可以是一个元件,也可以是一个电路,它的阻抗可以用Z=U1/I1Z=U_1/I_1Z=U1/I1表示。
现假设负载是图(b)所示点画线框内由变压器和电阻组成的电路,该负载的阻抗Z=U1/I1Z=U_1/I_1Z=U1/I1,变压器的匝数比为nnn,电阻的阻抗为ZLZ_LZL,根据变压器改变电压的规律U1/U2=I2/I1=nU_1/U_2=I_2/I_1=nU1/U2=I2/I1=n可得到下式,即
Z=U1I1=nU21nI2=n2U2I2=n2ZLZ=\frac{U_1}{I_1}=\frac{nU_2}{\frac{1}{n}I_2}=n^2\frac{U_2}{I_2}=n^2Z_LZ=I1U1=n1I2nU2=n2I2U2=n2ZL从上式可以看出,变压器与电阻组成电路的总阻抗ZZZ是电阻阻抗ZLZ_LZL的n2n^2n2倍,即Z=n2ZLZ=n^2 Z_LZ=n2ZL。如果让总阻抗ZZZ等于电源的内阻R0R_0R0,变压器和电阻组成的电路就能从电源获得最大功率,又因为变压器不消耗功率,所以功率全传送给真正的负载(电阻),达到功率最大程度传送的目的。由此可以看出:通过变压器的阻抗变换作用,真正负载的阻抗不需与电源内阻相等,同样能实现功率最大传输。
但是注意,负载获得最大功率时,电路的效率是很低的,理论上只有50%,所以传输效率并不高。但是在小功率的信号系统中,由于能量消耗并不大,因此在这种情况下,效率不再是关键因素,负载获得最大功率为首先要考虑的条件。