图论核心算法（C++）：包括存储结构、核心思路、速记口诀以及学习方法, 一站式上机考试学习【附PKU百练，相关练习题单】

部分图例参考于： 互联网， 如有版权问题，请告知，立即删除

作者：黄老师

一、图的存储结构

不同算法适配不同的存储结构，选择合适的存储方式是实现算法的基础：

1. 邻接矩阵（二维数组）

// 适用于稠密图，顶点数n较小的情况
const int MAXN = 1005;
int graph[MAXN][MAXN]; // graph[i][j]表示i到j的边权，无边时设为INF

• 特点 ：访问边的时间复杂度O(1)，空间复杂度O(n²)，适合顶点数少的场景（如Floyd算法）。
  

2. 邻接表（vector/链表）

// 适用于稀疏图，顶点数n大、边数m少的情况
const int MAXN = 1e5 + 5;
vector<pair<int, int>> adj[MAXN]; // adj[u]存储(u, v, w)，即u到v的边权为w

• 特点 ：空间复杂度O(m)，遍历邻接点高效，适合DFS/BFS/Dijkstra/Prim等算法。
  

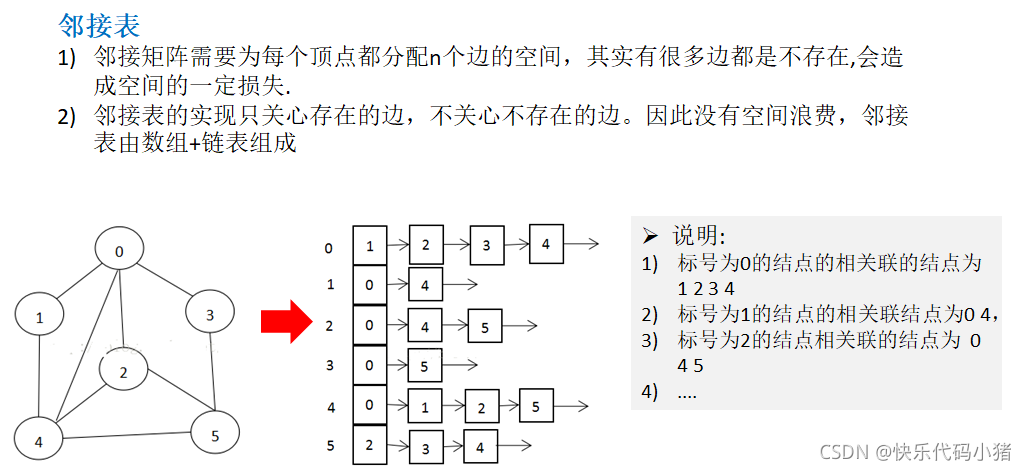
3. 边集数组（结构体数组）

// 适用于按边操作的算法（如Kruskal）
struct Edge {
    int u, v, w;
    bool operator<(const Edge& other) const {
        return w < other.w; // 按边权排序
    }
} edges[MAXM]; // MAXM为边数

• 特点：直接存储所有边，便于排序和筛选，是Kruskal算法的首选。

二、各算法详解（存储结构+核心思路+速记口诀）

1. 图的遍历：DFS（深度优先搜索）

存储结构

邻接表（优先）或邻接矩阵。

核心思路

• 从起点出发，沿着一条路径走到头（递归/栈实现）；
• 回溯后探索其他未访问的分支，标记已访问节点避免重复。

代码框架（邻接表）

bool visited[MAXN];
void dfs(int u) {
    visited[u] = true; // 标记访问
    for (auto& [v, w] : adj[u]) { // 遍历邻接点
        if (!visited[v]) {
            dfs(v); // 递归访问
        }
    }
}

速记口诀

"一条路走到黑，回头再探其他路"

2. 图的遍历：BFS（广度优先搜索）

存储结构

邻接表（优先）或邻接矩阵。

核心思路

• 从起点出发，先访问所有邻接点（第一层）；
• 再依次访问邻接点的邻接点（第二层），用队列实现"逐层扩散"。

代码框架（邻接表）

bool visited[MAXN];
void bfs(int start) {
    queue<int> q;
    q.push(start);
    visited[start] = true;
    while (!q.empty()) {
        int u = q.front(); q.pop();
        for (auto& [v, w] : adj[u]) {
            if (!visited[v]) {
                visited[v] = true;
                q.push(v);
            }
        }
    }
}

速记口诀

"队列排队，逐层扫荡，先近后远"

动画模拟BFS、DFS过程：

3. 最短路：Dijkstra（单源最短路径，无负权边）

存储结构

邻接表（优先）+ 优先队列（小根堆）。

核心思路

• 初始化起点到各点的距离为INF，起点距离为0；
• 用优先队列选当前距离最小的节点u，松弛其邻接点v（即dist[v] = min(dist[v], dist[u]+w)）；
• 重复直到所有节点处理完毕。

代码框架（邻接表+优先队列）

const int INF = 0x3f3f3f3f;
int dist[MAXN];
void dijkstra(int start, int n) {
    memset(dist, 0x3f, sizeof(dist));
    dist[start] = 0;
    priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq;
    pq.push({0, start});
    while (!pq.empty()) {
        auto [d, u] = pq.top(); pq.pop();
        if (d > dist[u]) continue; // 跳过已处理的旧节点
        for (auto& [v, w] : adj[u]) {
            if (dist[v] > dist[u] + w) {
                dist[v] = dist[u] + w;
                pq.push({dist[v], v});
            }
        }
    }
}

速记口诀

"小堆选近点，松弛邻接点，贪心找最短"

Prim算法，Kruskal算法，Dijkstra算法，Floyd算法的过程讲解

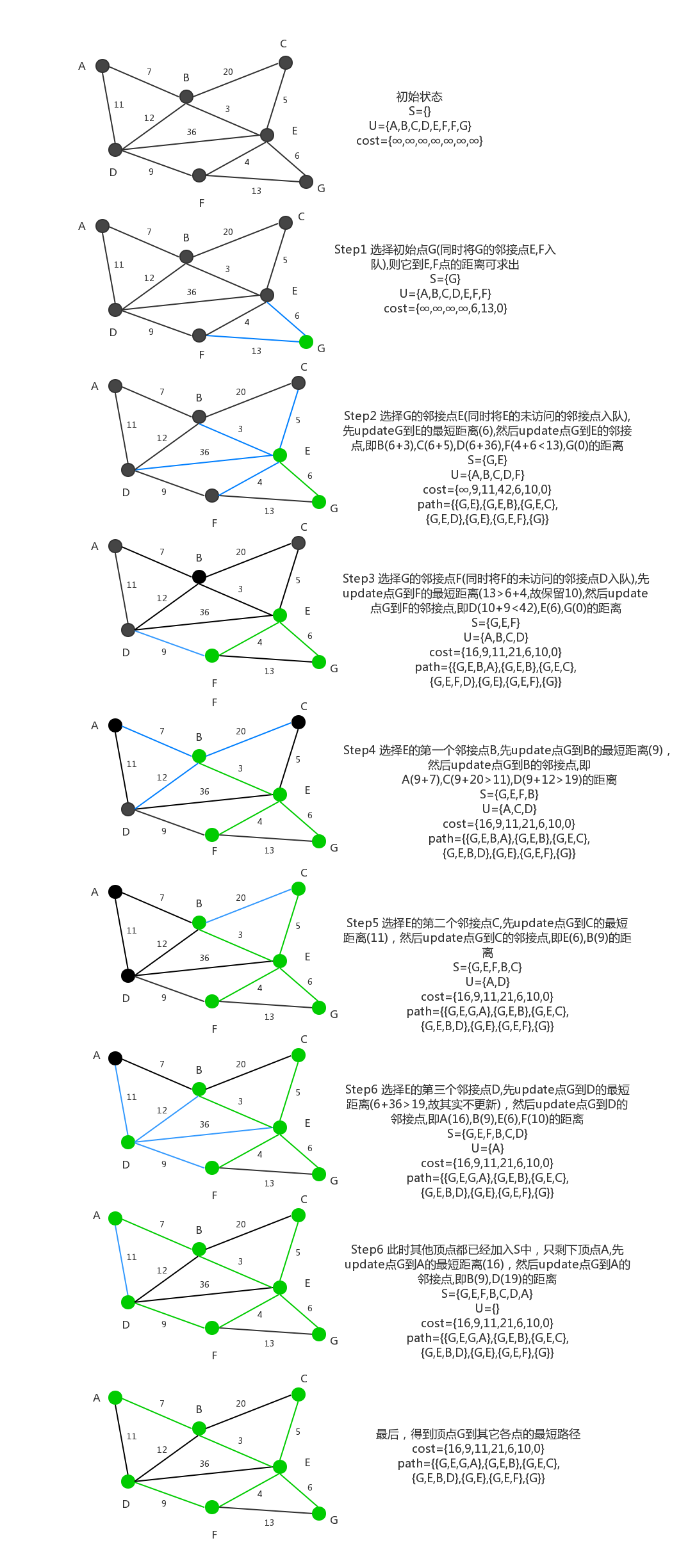
4. 最短路：Floyd（多源最短路径，允许负权边无负环）

存储结构

邻接矩阵（必须）。

核心思路

• 动态规划思想：dp[k][i][j]表示经过前k个节点时i到j的最短路径；
• 状态转移：dp[i][j] = min(dp[i][j], dp[i][k]+dp[k][j])（k为中转点）；
• 三层循环：枚举中转点k→起点i→终点j。

代码框架（邻接矩阵）

const int INF = 0x3f3f3f3f;
int dp[MAXN][MAXN];
void floyd(int n) {
    // 初始化dp为邻接矩阵
    for (int k = 1; k <= n; k++) { // 中转点
        for (int i = 1; i <= n; i++) { // 起点
            for (int j = 1; j <= n; j++) { // 终点
                dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j]);
            }
        }
    }
}

速记口诀

"中转点插中间，三层循环算遍，dp找最短"

5. 最小生成树：Prim（稠密图适用）

存储结构

邻接矩阵（稠密图）或邻接表+优先队列（稀疏图）。

核心思路

• 从任意起点出发，维护"已选点集合"；
• 每次选连接"已选集合"和"未选集合"的最小权边，将对应点加入集合；
• 重复直到所有点加入（共选n-1条边）。

代码框架（邻接表+优先队列）

const int INF = 0x3f3f3f3f;
int dist[MAXN]; // dist[v]表示v到已选集合的最小距离
bool visited[MAXN];
int prim(int n) {
    memset(dist, 0x3f, sizeof(dist));
    memset(visited, false, sizeof(visited));
    dist[1] = 0; // 从1号点开始
    int sum = 0; // 最小生成树总权值
    for (int i = 1; i <= n; i++) {
        // 选未访问的最小dist节点
        int u = -1;
        for (int j = 1; j <= n; j++) {
            if (!visited[j] && (u == -1 || dist[j] < dist[u])) {
                u = j;
            }
        }
        visited[u] = true;
        sum += dist[u];
        // 更新邻接点到已选集合的距离
        for (auto& [v, w] : adj[u]) {
            if (!visited[v] && w < dist[v]) {
                dist[v] = w;
            }
        }
    }
    return sum;
}

速记口诀

"选点扩集合，贪最小边连，n-1边成团"

6. 最小生成树：Kruskal（稀疏图适用）

存储结构

边集数组（必须）+ 并查集（判环）。

核心思路

• 将所有边按权值从小到大排序；
• 依次选边，若边的两个端点不在同一连通分量（用并查集判断），则加入生成树；
• 重复直到选n-1条边。

代码框架（边集数组+并查集）

struct Edge { int u, v, w; };
Edge edges[MAXM];
int parent[MAXN];

// 并查集查找（带路径压缩）
int find(int x) {
    return parent[x] == x ? x : parent[x] = find(parent[x]);
}

int kruskal(int n, int m) {
    sort(edges, edges + m); // 按边权排序
    for (int i = 1; i <= n; i++) parent[i] = i; // 初始化并查集
    int sum = 0, cnt = 0; // sum总权值，cnt选边数
    for (int i = 0; i < m; i++) {
        int u = edges[i].u, v = edges[i].v, w = edges[i].w;
        int fu = find(u), fv = find(v);
        if (fu != fv) { // 不连通则合并
            parent[fu] = fv;
            sum += w;
            cnt++;
            if (cnt == n-1) break; // 选够n-1条边
        }
    }
    return sum;
}

速记口诀

"边排序选小，并查集判环，连n-1边好"

动画演示：

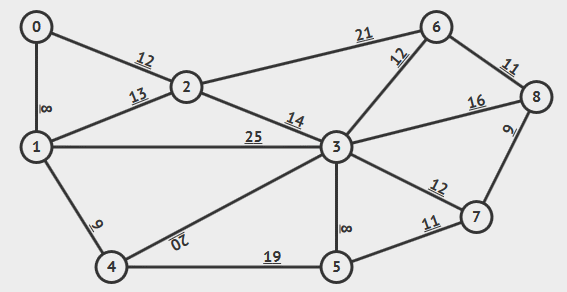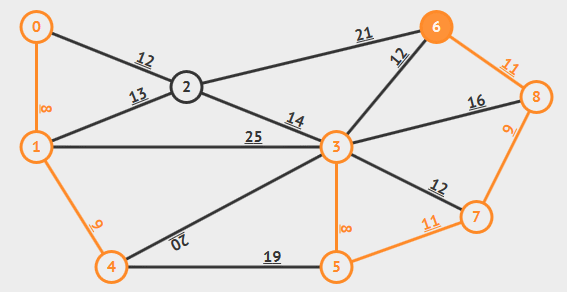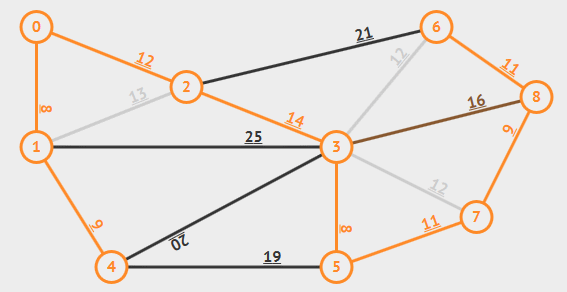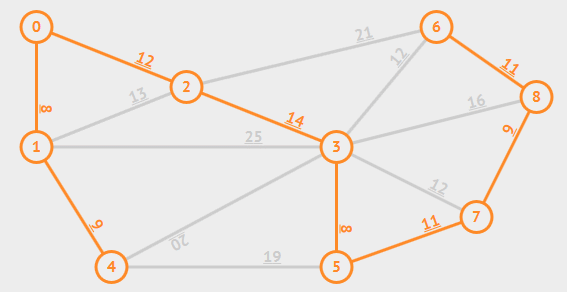
7. 拓扑排序：Kahn算法（处理DAG）

存储结构

邻接表（存边）+ 入度数组（存节点入度）。

核心思路

• 初始化队列，将入度为0的节点入队；
• 取出队首节点u，加入拓扑序列，遍历其邻接点v，将v的入度减1；
• 若v的入度变为0则入队，重复直到队空；
• 若拓扑序列长度≠节点数，说明有环。

代码框架（邻接表+入度数组）

vector<int> adj[MAXN];
int in_degree[MAXN];
vector<int> topo_sort(int n) {
    queue<int> q;
    vector<int> res;
    for (int i = 1; i <= n; i++) {
        if (in_degree[i] == 0) q.push(i);
    }
    while (!q.empty()) {
        int u = q.front(); q.pop();
        res.push_back(u);
        for (int v : adj[u]) {
            in_degree[v]--;
            if (in_degree[v] == 0) q.push(v);
        }
    }
    return res; // 若res.size() < n则有环
}

速记口诀

"入度零入队，删边减度数，依次排顺序"

参考：

8. 关键路径算法（处理DAG的最长路径）

存储结构

邻接表（存边）+ 逆邻接表（用于求ve/vl）。

核心思路

• 步骤1 ：拓扑排序，求事件最早发生时间ve[i]（ve[v] = max(ve[v], ve[u]+w)）；
• 步骤2 ：逆拓扑排序，求事件最迟发生时间vl[i]（vl[u] = min(vl[u], vl[v]-w)）；
• 步骤3：计算活动最早/最迟开始时间，若相等则为关键活动，关键活动组成关键路径。

速记口诀

"拓扑算ve，逆序算vl，相等是关键"

三、算法速查表

算法	存图结构	核心 3 步	口诀（10 字内）	模板行数	核心思想
DFS/BFS	邻接表 vector<int> g[N]	1.队列/栈 2.访标记 3.拓邻居	"栈深队广，标邻"	10 行	搜索（回溯/广度优先）
Dijkstra	邻接表 vector<P> g[N]	1.小根堆 2.松弛 3.vis 防重	"堆松 vis"	15 行	贪心算法
Floyd	矩阵 int d[N][N]	1.自环初值 2.kij 中转 3.更优更新	"kij 中转"	5 行	动态规划
Prim	邻接表 vector<P> g[N]	1.小根堆 2.跨边入堆 3.累加答案	"跨边堆"	15 行	贪心算法
Kruskal	边集 vector<Edge> e	1.按权排序 2.并查加边 3.n-1 结束	"排并加"	12 行	贪心算法 + 并查集
Khan 拓扑	邻接表 + 入度数组	1.入度 0 入队 2.删边降度 3.队空判环	"0 队降"	12 行	拓扑排序（贪心）
关键路径	邻接表 + 逆邻接表	1.拓扑正序算 ve 2.逆序算 vl 3.边 e=l=ve, l=vl-w, 关键=e==l	"正 ve 逆 vl"	20 行	动态规划 + 拓扑排序

四、学习总结与推荐

学习步骤推荐

1. 先把口诀抄三遍，读出声，强化核心逻辑记忆；
2. 把模板打印，在空白处默写核心3步，理解算法骨架；
3. 上机刷5~10道经典裸题，巩固代码实现能力。

经典练习题单

算法	百炼题号（标题）	直达链接
DFS/BFS	2810 - 迷宫问题	https://bailian.openjudge.cn/practice/2810
BFS 最短路	2796 - 骑士移动	https://bailian.openjudge.cn/practice/2796
Dijkstra	2724 - 最短路	https://bailian.openjudge.cn/practice/2724
Floyd	2725 - 全源最短路	https://bailian.openjudge.cn/practice/2725
Prim	2727 - 最小生成树	https://bailian.openjudge.cn/practice/2727
Kruskal	2728 - 丛林之路	https://bailian.openjudge.cn/practice/2728
Khan 拓扑	2722 - 拓扑排序	https://bailian.openjudge.cn/practice/2722
关键路径	2730 - 关键路径	https://bailian.openjudge.cn/practice/2730
综合 DFS+剪枝	2692 - 八皇后问题	https://bailian.openjudge.cn/practice/2692
综合 最短路+堆优化	2757 - 网络延时	https://bailian.openjudge.cn/practice/2757

总结

• 存储结构选型：邻接表适配多数遍历/最短路径/生成树算法，邻接矩阵是Floyd专属，边集数组为Kruskal定制；
• 算法核心逻辑：DFS/BFS是遍历基础，Dijkstra/Floyd解决最短路径，Prim/Kruskal构建最小生成树，拓扑排序处理DAG依赖，关键路径分析DAG最长路径；
• 学习关键方法：口诀记核心、模板搭骨架、刷题练实战，三步结合可高效掌握图论算法。

视频学习资源：
图论:最小生成树之kruscal算法-哔哩哔哩
图论:最小生成树之prim算法-哔哩哔哩
最短路径算法(BFS、Dijkstra、Floyd)-哔哩哔哩
C++ 图论的基础概念-哔哩哔哩
图论:最短路算法之Dijkstra(堆优化版)| 迪杰斯特拉算法-哔哩哔哩